基于卷积神经网络和贝叶斯算法的驾驶员状态监测研究
2021-12-24魏翼鹰徐劲力
杨 涛 吴 波 魏翼鹰 徐劲力
(武汉理工大学机电工程学院 武汉 430070)
0 引 言
对驾驶员驾驶状态进行监测并对不安全行为进行提醒可以减少驾驶员的分神状态.数据表明,在交通事故发生前,如果驾驶员的反应比疲劳时快0.5 s,则60%的事故可以避免[1-3];同时针对某些区域如大型企业内的行驶安全问题,在内部车辆安装驾驶员状态监测设备,可对企业车辆行驶状态进行监测,且对驾驶员有警醒作用,可降低企业内部区域的事故发生率,规范驾驶员驾驶行为.
近年来,人工神经网络(ANN)作为人工智能的代表被广泛应用在各个领域,其中卷积神经网络(CNN)由于其引入特有的先验知识——深度网络、局部连接和参数共享,在图像识别领域具有独特的优势.但随着卷积神经网络不断发展,其深度不断增加、网络结构更加复杂,使得训练一个优秀的神经网络的计算成本十分高昂,迁移学习的出现很好的解决了这一问题.迁移学习从宏观角度可以理解为:任务A中学得的知识可以用到任务B中,从而降低任务B的学习难度;从网络结构上理解,迁移学习是指对已经训练好的模型进行末尾全连接层的重新定义,并重新训练部分网络层,从而减少训练量与训练时间,节省计算成本,因此采用迁移学习方式完成驾驶员状态监测这一任务是可行的.针对卷积神经网络算法中存在的大量超参数,若采用人工调参将十分耗时耗力,因此采用自动化调参算法对迁移学习模型进行参数优化可以节省运算成本,提高模型准确率.
文中采用卷积神经网络中的迁移学习方式对驾驶员状态进行监测,利用混合数据集方式解决国内驾驶员状态监测数据集空缺问题,采用贝叶斯算法进行神经网络超参数优化,实现对驾驶员状态的高准确率监测.
1 卷积神经网络
1.1 卷积神经网络模型
卷柜神经网络迁移学习模型采用已经在ImageNet数据集训练完成,并集成于keras中的Mobilenet_V2[4]模型,Mobilenet_V2是一种轻量化网络模型,采用的线性瓶颈层和颠倒残差结构,在保持精度的同时大大减少了计算量,拥有较好的嵌入式性能.文中在Mobilenet_V2的基础上对其最后几层进行优化,使模型具有更好的学习能力,表1为优化后的Mobilenet_V2网络框架.
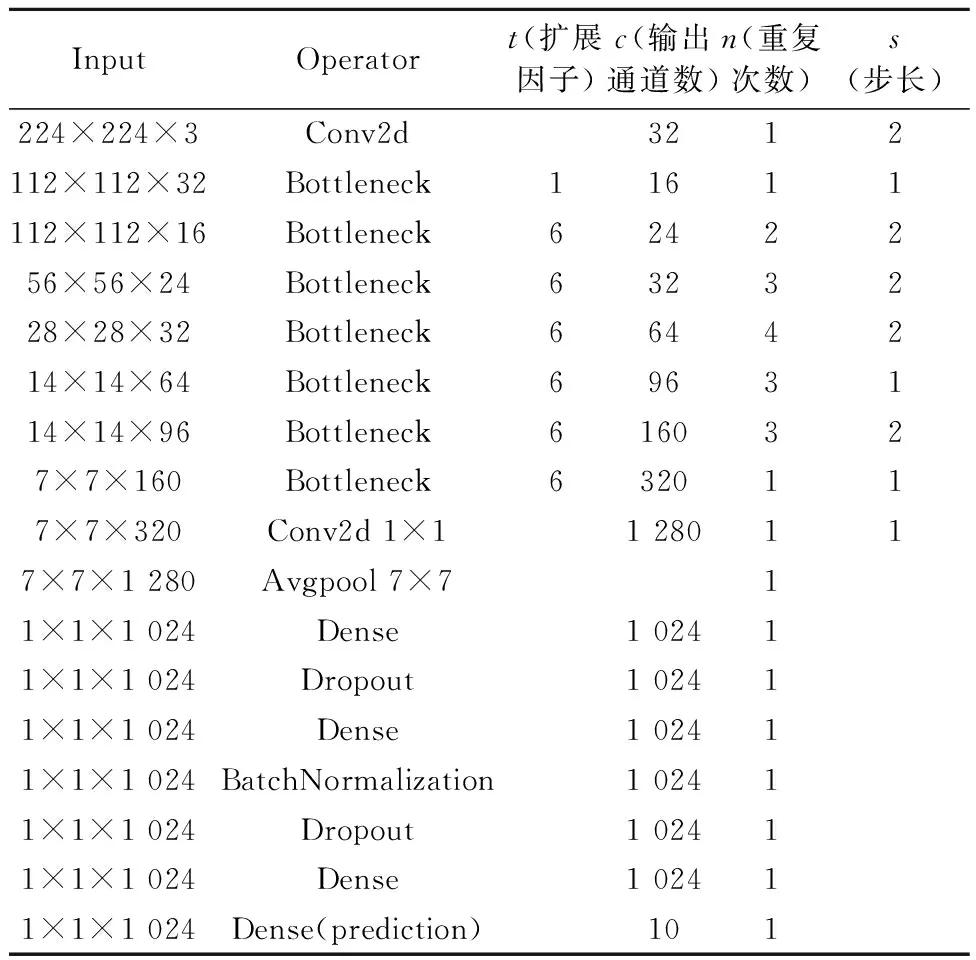
表1 Mobilenet_V2网络框架
1.2 数据集建立
训练CNN模型的数据集主要来源于Kaggle的State Farm Distracted Driver Detection数据集,该数据集将驾驶员状态分为10类,分别编号为0~9,编号0为正常状态,编号1~9均为驾驶员非正常状态,但由于肤色等人种外貌差异,该数据集在中国汽车驾驶员状态监测任务中的适用性较差.为了减少由于人种差异而带来的误差,在Kaggle数据集的基础上,在训练集及测试集都加入一定数量中国汽车驾驶员状态数据图片,构成混合数据集.
1.3 迁移学习模型
由于数据集图片的特征较多,如果只训练神经网络模型全连接层,模型很难找到数据特征,因此需要在全连接输出层之前开始训练,采用Fine-tune迁移学习方式,即锁定部分卷积层,更改全连接层输出,重新训练输出与未锁定的部分卷积层[5];同时由于训练集数据的差异性较小、学习模型学习特征较多等原因,需要进行一定的操作来防止过拟合.
1.3.1损失函数的选择
为了加大对错误数据的惩罚力度,神经网络一般采用交叉熵损失.交叉熵损失通过惩罚错误的分类,实现对分类器的准确度的量化,最小化交叉熵损失基本等价于最大化分类器的准确度.为了计算交叉熵损失, 分类器必须提供对输入的所属的每个类别的概率值, 不只是最可能的类别[6],交叉熵损失函数为
LgLoss=L(Y,P(Y|X))=-lgP(Y|X)=
(1)
式中:Y为输出变量;X为输入变量;L为损失函数;N为输入样本量;M为可能的类别数;yij为一个二值指标,为类别j是否是输入实例xi的真实类别;pij为模型或分类器预测输入实例xi属于类别j的概率模型优化器.
1.3.2防止过拟合
1) 数据增强 对训练集数据进行旋转、平移、适当裁剪、灰度变换等操作,增加训练集数据的多样性;同时加入一定量的不同车、人、视角等图片置于训练集.
2) 采用dropout方式,对训练过程中的部分神经元权重进行随机丢弃,缩减参数量,避免过拟合,dropout方式经过长时间的实践检验证明可以有效防止过拟合[7].
3) 加入正则化系数进行正则化,加入BN层.
1.3.3模型优化器
采用Adam优化器.Adam结合了AdaGrad和RMSProp两种优化算法的优点,对梯度的一阶矩估计和二阶矩估计进行综合考虑,计算出更新步长,从而进行参数优化的方法.该方法易于实现,计算效率高,内存要求小,适用于具有大数据或大参数、非平稳目标或具有非平稳目标、具有嘈杂或稀疏梯度的问题,同时该方法的超参数有直观的解释且调优简便[8].
1.3.4超参数优化
包括batch_size、模型学习率lr、dropout、正则化系数,以及开始Fine-tune的网络层数等.
针对神经网络超参数进行优化的算法包括网格搜索法(grid search)、随机搜索法[9](random search)及贝叶斯优化算法[10](Bayesian optimization).本文选用贝叶斯优化算法.
2 贝叶斯算法
贝叶斯优化算法基于目标函数的历史评估结果去建立目标函数的概率代理模型,从而寻找最小化目标函数的参数值.
贝叶斯优化算法有两个核心内容,即概率代理模型(PSM)和采集函数(AC),概率代理模型根据概率框架对参数的不确定性进行建模,包含先验概率模型和观测模型,概率代理模型通过对先验概率进行观测,从而获得包含更多先验的后验概率分布.采集函数由已观测数据得到的后验概率分布构成,通过最大化采集函数从而获得下一个最有“潜力”的参数评估点.
贝叶斯优化算法的目标在于最小化目标函数值,为
x=argminx∈X⊆Rf(x)
(2)
f(x)=Loss(Tv,x)+ε
(3)
Loss(Tc,x)可用如下伪代码表示:
def Loss(Tc,x):
迁移学习模型(含有超参数x);
训练集训练;
验证集Tv验证输出Loss;
return logloss.
式中:f(x)为目标函数;Tv为验证集;Loss()为损失函数(文中为式(1)的lgloss函数);x为超参数;X为超参数域空间.
由于处于优化过程,模型超参数x在算法终止前始终处于优化状态,因此真实的目标函数f(x)是未知的,当贝叶斯优化算法终止时,超参数达到最优,此时目标函数为已知,即为所求的最优化模型.
2.1 概率代理模型
依据模型是否有固定的参数集,概率代理模型分为参数模型和非参数模型.常用的参数模型有贝塔-伯努利模型、线性模型及广义线性模型,非参数模型有高斯过程、随机森林、深度学习网络及Tree Parzen Estimators(TPE)[11]方法,由于TPE方法自身支持具有指定域空间的超参数,因此采用TPE构建概率模型.
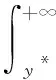
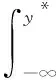
TPE方法与其他方法区别在于:TPE并不为目标函数f(x)构建预测概率模型,而采用式(4)的密度为所有的域变量生成概率模型.
(4)
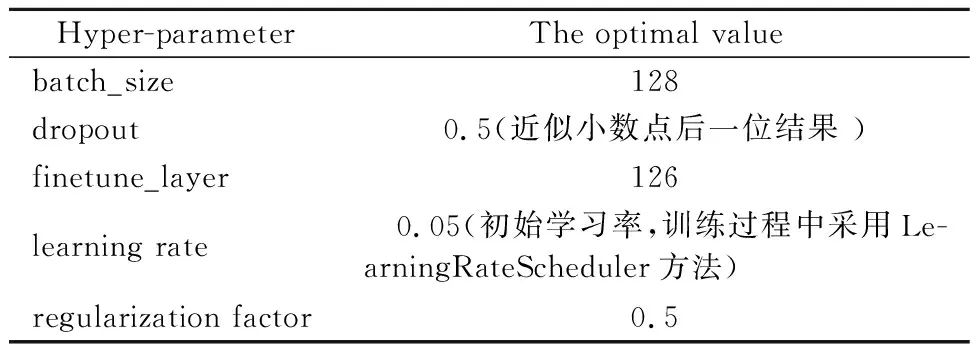
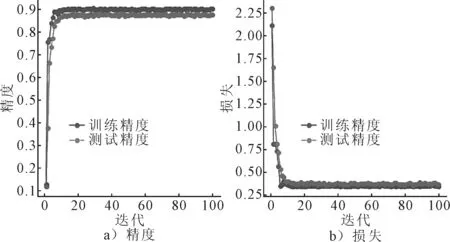
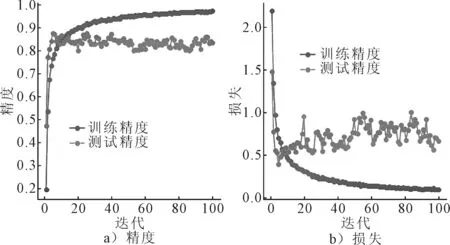
式中:y*=min{f(xt),1≤t 常用的采集函数有三类,基于提升的策略:PI、EI;基于信息的策略:汤普森采样、熵搜索采样、熵预测采样;置信边界策略及组合策略.文中采用基于提升策略中的Expected Improvement(EI)方法作为采集函数,并对其进行优化.EI为关于x映射到实数空间R的期望函数,具有参数少、 在一定程度上可以平衡探索(exploration)与开发(exploitation)的优点. (5) (6) (7) 将式(6)、式(7)代入式(5)中可得: (8) 为了最小化目标函数f(x),即希望x尽可能位于l(x)区域,从而β较大,因此通过最大化EIy*(x),从而得到评估点x(i). x(i)=argmax(EIy*(x)) (9) 采用的贝叶斯算法优化超参数方法为 步骤1input∶f、X、AC、PSM 步骤2H0←INITIALIZE(f、X) 步骤3for i←1 to t: 步骤4f(x)←TPE(Ht-1) %p(x|y,H)←FITMODEL(H,PSM) 步骤5x(i)=argmax(EIy*(x)) 步骤6y*=min(f(xi),H) 步骤7H←H∪(x*,y*) 步骤8end for 步骤9return argmin(g∈Ht) (g,Tv) 实验软件采用基于pycharm2018,python3.5版本的jupyter开发环境,结合keras2.2.0框架.硬件工作站处理器为Intel Core i9-8950 CPU,运行速度2.9 GHz,GPU为NVIDIA Quadro P2000,内存32 GB. Mobilenet_V2迁移学习模型中的超参数及其域空间见表2. 表2 Mobilenet_V2迁移学习模型超参数及其域空间 采用贝叶斯优化算法对模型进行超参数优化,优化结果见表3. 表3 超参数优化结果 将表3中贝叶斯算法优化的超参数代入神经网络模型,经训练观察其loss与accuracy变化,并与随机搜索算法优化结果进行对比(网格搜索法由于实际应用时计算量成本特别大,因此不常用于大样本深度学习参数优化,因此文中试验不进行网格搜索法的优化). 相较于随机搜索算法,在算法运行时间方面,贝叶斯算法运行时间为随机算法的60%.在模型优化结果方面(见图1~2),贝叶斯优化结果模型更加收敛,模型没有出现过拟合现象,验证集准确率在86%以上,高于随机算法结果.在模型损失方面,贝叶斯结果验证损失为0.35,低于随机算法结果;综合对比之下,贝叶斯算法更具优势. 图1 贝叶斯算法参数模型图表 图2 随机搜索算法参数模型l图表 对贝叶斯最优模型进行可靠性实验,从测试集中抽取200张图像构建模型测试集,准确率实验结果见表4. 表4 模型测试准确率图表 将模型用于监测驾驶员状态,采用类激活映射图(CAM)以更直观观测,结果见图3. 图3 类激活映射图(CAM图特征区域中,灰度值约小区域表示该区域激活值更大) 由图3可知,驾驶员状态图像中,特征重要区域的激活值明显大于其他区域的激活值,因此可以看出经过贝叶斯算法优化后的神经网络模型,在学习类别特征时能自主的学习重要区域的特征,对于非重要区域的特征少学习或不学习. 综上所述,贝叶斯算法能够提供极好的模型超参数,使得模型在具有良好的泛化性能,对于驾驶员状态的检测也能够达到预期目标. 针对汽车行驶过程中驾驶员状态监测问题,文中采用了一种基于迁移学习方式的解决方法,并采用贝叶斯算法对其进行超参数优化,根据最终的实验结果,该方法对于中国汽车驾驶员具有较高的识别准确率.但文中方法也有不足,该方法在一定的环境下对驾驶员状态具有较高的识别准确性,但当车辆外部环境较为复杂且车窗打开时,识别准确率有所降低,下一步的研究重点将是采用一定的数据处理方式降低周边噪声对结果的影响.2.2 采集函数





2.3 文中贝叶斯优化算法的实现
3 实验与结果分析

3.1 贝叶斯算法优化结果与分析
3.2 迁移学习模型
3.3 实验与结果分析


4 结 束 语
