卷积神经网络的卷积加速算法分析
2021-12-24刘佶
刘 佶
(山西职业技术学院,山西 太原 030006)
0 引言
卷积神经网络是目前人工智能领域最前沿的深度学习算法之一,被广泛应用在自然语言处理、图像识别等多个领域。卷积层这一重要组成部分主要由卷积运算实现,但由于资源消耗严重,故在高实时性的应用场合很难满足数据处理时间的要求。因此,研究人员使用了各种算法加速卷积,以提高其在视频流处理、高速运动物体识别等应用场合的实时性。本文介绍了卷积运算的加速算法,详述其理论基础,介绍了这些算法在几个经典卷积神经网络架构中体现出的效果,并提出了对加速算法实现方式的展望。
1 卷积神经网络中的卷积运算
卷积神经网络的卷积通常为二维的输入矩阵x与二维的卷积核矩阵w运算,其输出为二维矩阵[1]。输出矩阵的元素s(i,j)计算公式如下:
S(i,j)=∑m∑nx(i+m,j+n)×w(m,n) .
(1)
卷积可以看作大小与w相同的窗口在x上滑动,将每次取出的矩阵与w对应位置相乘并累加乘积,填入输出矩阵中。以4×4的输入矩阵与2×2的卷积核为例(本文使用⊗表示卷积运算,下同)。

图1 传统卷积
2 基于FFT的卷积运算
快速傅里叶变换(FFT)是使计算机便于执行离散傅里叶变换(DFT)产生的算法。利用递归,最终可将一个多点FFT拆成若干个2点FFT[2]。
二维矩阵的FFT,则是先将每一行进行FFT之后,将变换完的矩阵每一列再进行FFT运算。
LeCun等人将FFT应用到了卷积神经网络当中,实现了传统卷积的加速[3],使用如下公式实现卷积:
x⊗w=IFFT(FFT(x)×FFT(w))
(2)
即将输入矩阵与卷积核分别做FFT的结果再做数乘,得到结果进行逆FFT运算。需要说明的是,为了使两矩阵可直接相乘,需填充0使其大小一致。以4×4的输入矩阵与2×2的卷积核所作的卷积为例,如图2。
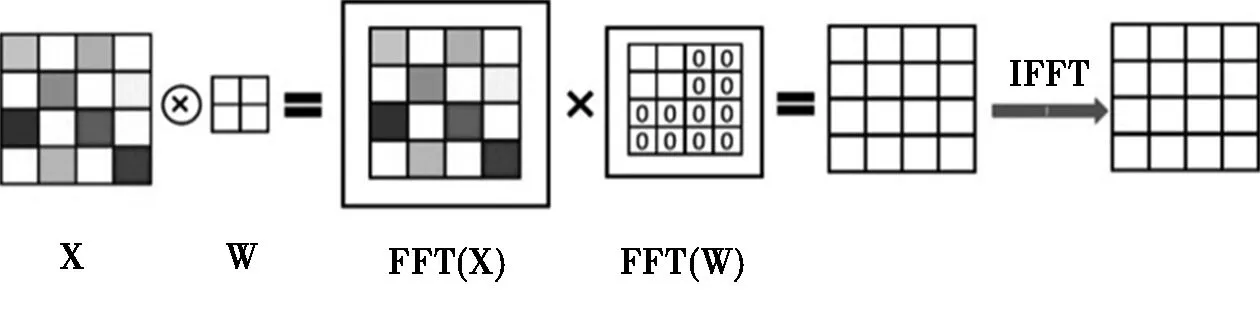
图2 基于FFT的卷积
3 基于OVA-FFT的卷积运算
Highlander等人提出了基于OVA-FFT的卷积在卷积神经网络中的应用,计算224×224的输入矩阵与8×8的卷积核的卷积,比传统卷积的运算速度快了16.3倍[4]。其核心思想是将输入矩阵在做FFT前分割为尺寸与卷积核相同的若干子矩阵,每个子矩阵分别与卷积核做基于FFT的卷积运算,再将得到的矩阵按照分割输入矩阵的方式拼接。其公式如下:

(3)
使用4×4的输入矩阵与2×2的卷积核所作的卷积操作为例。
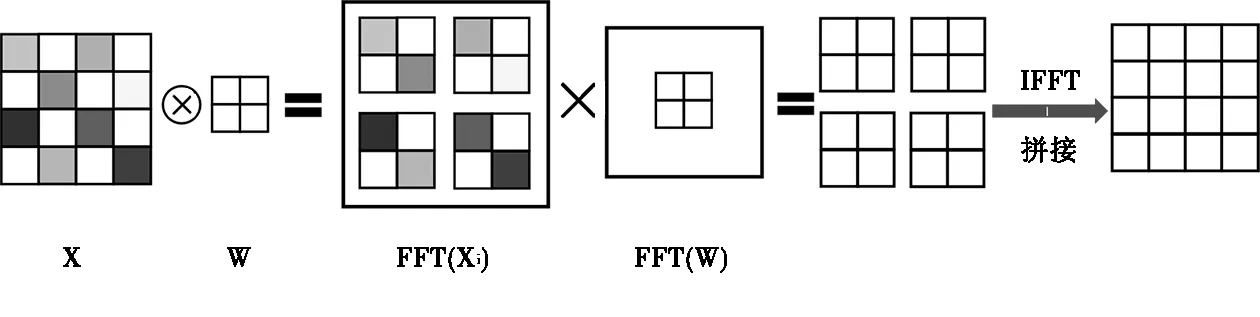
图3 基于OVA-FFT的卷积
4 基于Winograd算法的卷积运算
Andrew Lavin等人研究了基于Winograd的卷积运算,与GPU实现的卷积相比在不同尺寸输入矩阵上都体现了加速[5],并详述了一维的Winograd算法,本文使用4×4的输入矩阵与3×3的卷积核详述二维运算。
如图4,窗口截取的数排成矩阵的一行,最终可写为两矩阵的乘法。在过程中会计算:

图4 基于Winograd的卷积
r1=x1×w1+x2×w2+x3×w3
(4)
r2=x2×w1+x3×w2+x4×w2
(5)
使用配项提取公因式,可以将公式变形为:
r1=(x1-x3)w1+(x2+x3)×(w1+w2+w3)/2+(x3-x2)×(w1-w2+w3)/2 .
(6)
r2=(x2+x3)×(w1+w2+w3)/2-(x3-x2)×(w1-w2+w3)/2-(x2-x4)w2.
(7)
由于元素和重复存在于两个表达式中,使得运算量比起直接卷积降低。
如果令
可以看出该算法使用x和w构造出2个中间向量,使用它们的乘积得到卷积结果。如果将x′和w′看作某种变换,那么它的思想与基于FFT的卷积非常相似,即先将两个向量转换到变换域做简单运算,再反变换得到结果。
5 运算量分析及对比
5.1 运算量分析
假定卷积运算的输入为一尺寸为n×n的图片和k×k(k 根据传统卷积运算理论,移动窗口共计为(n-k+1)2。每个大小为k×k的窗口与卷积核进行运算,需k2次乘法。因此完成卷积所需的乘法运算总数为(n-k+1)2×k2。算法复杂度为O(n2k2)。 使用基于FFT的卷积,n×n矩阵完成FFT需n2log2(n)次复数乘法,变换后的矩阵相乘需n2次复数乘法,IFFT需n2log2(n)次复数乘法。因此,完成卷积共需3n2log2(n)+n2次复数乘法。考虑到一次复数乘法需4次实数乘法,则共需12n2log2(n)+4n2次实数乘法。算法复杂度为O(n2log2(n))[1]。 使用基于Winograd的卷积,最终转换成两n×n矩阵的数乘。根据Andrew Lavin等人的分析[5],生成x′和w′过程可以预先完成,运算开销在n比较大的情况下可忽略。因此,需要的乘法次数为n2,算法复杂度为O(n2)。 通过5.1可以得出,大卷积核会使基于FFT的卷积有加速效果,基于OVA-FFT的卷积可使运算量进一步降低,但仍超过基于Winograd的卷积。 Abtahi 等人将传统卷积、基于FFT的卷积和基于OVA-FFT的卷积在ResNet-20和AlexNet两种卷积神经网络中进行了运算量对比[1],Lavin等人将基于FFT的卷积和基于Winograd的卷积在VGG卷积神经网络中进行了对比[5],与上述分析结论一致。 传统卷积循环复杂,存在许多从运算结构、数据重复利用方面优化的可能性,再加上所作的基本操作为实数的乘累加,这种算法比较适合在FPGA上实现[5-8]。而基于Winograd和FFT的卷积,核心是域的变换,并且涉及到了复数运算,更加适合在已有大量优化算法库的CPU或GPU上部署。目前有相当数量的研究人员研究用FPGA实现各种加速算法。大家在结合FPGA特点的基础上,考虑了数据形式、流水线结构、存储资源扩展、高速接口等方面的因素。性能的提高,往往付出了更多的资源代价,最后会受到限制。总的来说用FPGA实现加速算法,是一个整体性工程,需要软件和硬件协同配合。 从当前实现的方式看,GPU和CPU+FPGA的架构仍会占较大比例。GPU的运算速度快,但功耗大。CPU+FPGA架构结合了两者的特点,利用了CPU灵活性和FPGA的运算速度。尤其目前高端FPGA中内嵌了CPU核,提升了开发便捷性。它在未来一段时间可能是主流的、尤其是低功耗应用场景的卷积神经网络实现平台。 卷积神经网络作为人工智能领域的一个重要研究分支,其应用范围越来越广,对其计算速度要求也越来越高。随着性能的提高,势必带来对存储容量、传输带宽、系统功耗的更高要求。对于加速算法来说,必须同时考虑到以上所有随之而来的影响,才会有其实际的应用价值。
5.2 运算量对比
6 算法实现平台分析
7 结束语
