刚度-阻尼-质量分布对CFRP板架式筏架减振性能影响分析
2021-12-24张锦光李弋文
马 磊,张锦光,李弋文,邓 伟
(武汉理工大学 机电工程学院,湖北 武汉 430070)
隔振装置能够有效降低舰船的机械噪声,其中浮筏隔振系统能够有效控制振动能量在系统中的传递,大幅减少动力装置产生的振动和噪声,以其安装空间小,浮筏结构设计方式灵活等特点被广泛应用于舰艇的动力设备隔振中[1-2]。
如图1所示,浮筏隔振系统由上层隔振器、筏架、下层隔振器和基座组成。其中机组设备通过上层隔振器与筏架弹性连接,筏架再通过下层隔振器与基座弹性连接。浮筏隔振系统的减振性能受多方面因素影响,主要有隔振器的刚度、阻尼,中间筏架质量、刚度、阻尼以及基座的弹性等[3]。随着舰船设备的多样化,对筏架的综合性能要求也越来越高,在保证隔振性能的情况下,传统金属筏架质量也相应地增加,从而加重了舰船的负载。
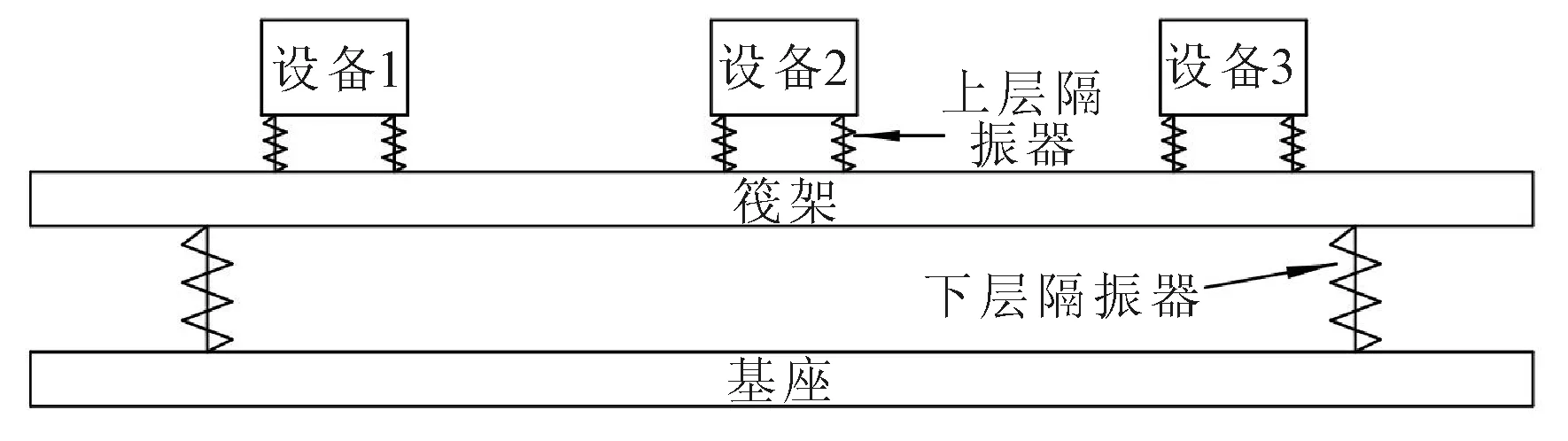
图1 浮筏隔振系统示意图
在被动隔振方面,筏架的隔振性能通常从两个方向进行优化:一是筏架结构的设计,二是新型材料的应用。
筏架结构主要有板架式、桁架式、摇篮式和周期结构式。司贵海等[4]提出了一种新型的间断肋式筏架结构,与传统浮筏相比其隔振性能更优越,特别是在中高频段具有突出效果。陈斌等[5]研究了三韧带手性周期结构的振动带隙特性,结果显示当振动频率处于结构的带隙范围内时,手性结构具有良好的振动衰减特性。黎上达等[6]分析了板架式筏架的高度、长宽比、腹板数目对浮筏隔振系统隔振效果的影响,结果表明调整结构几何参数可以改变其固有频率从而有效避开机械设备的激振频率。
在筏架的材料应用上,主要有金属、复合材料和阻尼夹层等。树脂基复合材料具有比强度高、比模量大、阻尼比高、耐疲劳等性能特点,其阻尼性能相比于金属要高一到两个数量级[7],并且由于其材料性能各向异性,可以根据不同的承载要求设计不同的结构和铺层方式。陈炉云等[8]建立了基于金属-复合材料的材料选型结构动力学优化模型,计算优化了筏架各区域的铺层材料选型和材料厚度,使得输出端最大功率流幅值减少8 dB。吕林华等[9]采用优化设计方法研究了钢-复合材料组合结构基座设计机理,结果表明组合基座比钢基座具有更好的隔振效果,复合材料的引入能提高基座的减振效果。
现有研究主要针对金属-复合材料组合的刚度、质量分布,对复合材料阻尼分布对浮筏系统减振效果的影响研究较少,结构阻尼多采用统一化处理。但对于纤维增强复合材料,铺层变化导致刚度变化的同时也伴随着阻尼性能的变化[10-11]。笔者设计了一种含有工字形支撑的板架式筏架,通过模态应变能法计算了筏架各组件不同铺层下的阻尼比,应用有限元法分析了CFRP(carbon fibre reinforced plastics)-钢质不同组合形式的筏架减振效果,为筏架刚度-阻尼-质量的一体化设计提供了理论分析验证。
1 CFRP筏架组件刚度计算
板架式筏架组件中筏架上/下板、工字形支撑主要由层合板构成,其组件的各向刚度可通过层合板的刚度参数来表征。在0~90°之间以15°为间隔共取7组对称铺层方案,材料参数如表1所示,纤维在各组件上的铺设方向如图2和图3所示,其中1为纤维0°方向,1′为与0°方向成θ角的纤维铺层方向;2(2′)为与纤维方向垂直的方向,3(3′)为厚度方向,根据对称铺层层合板正则化刚度计算公式[12],其1、2方向的弯曲刚度D11、D22如表2所示。

表1 T700/YPH-308型碳纤维预浸布的材料参数

图2 筏架上/下板纤维铺层坐标系

图3 工字形支撑纤维铺层坐标系

表2 组件层合板铺层及弯曲刚度
2 CFRP筏架组件阻尼比计算
根据Adams-Bacon阻尼模型,在一个振动周期内,结构总的能量损耗可以看作纤维方向、垂直方向以及剪切方向损耗应变能的总和。阻尼比容量定义为一个振动周期内系统的耗散能与最大应变能的比值[13]:
D=2πη=ΔU/U
(1)
式中:D为系统的阻尼比容量;η为系统的阻尼损耗因子;ΔU和U分别为每个振动周期内系统耗散的能量和储存的最大应变能。
阻尼损耗因子η与振动系统中阻尼比ζ在模态频率处的关系为[14]:
η=2ζ
(2)
在有限元模型中,结构总的应变能可表示为单元单位体积应变能的积分:
(3)
若已知各方向阻尼损耗因子,则结构的耗散能为:
(4)
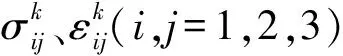
对于薄板结构,层合板的阻尼主要来自于面内应力σ11、σ22、σ12的贡献,而层间应力σ33、σ13、σ23对阻尼的贡献很小可以忽略不计,只需考虑η11、η22、η123个独立的阻尼损耗因子参数[15-16],笔者根据所使用材料的纤维/树脂组分含量等微观因素经实验测得后可分别取0.82%、2.98%、8.57%[13]。
在有限元软件ABAQUS中对筏架各组件进行模态分析,其一阶弯曲模态振型分别如图4和图5所示。导出该模态下各单元的应力、应变分量,在Matlab中按式(3)、式(4)编写相应程序计算各组件在该模态下的阻尼比ζ,计算结果如表3所示。筏架上/下板及工字形支撑一阶弯曲固有频率及阻尼比如图6、图7所示。
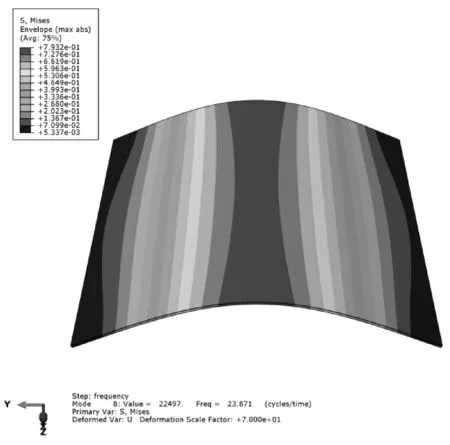
图4 筏架上/下板1阶弯曲模态

图5 工字形支撑1阶弯曲模态
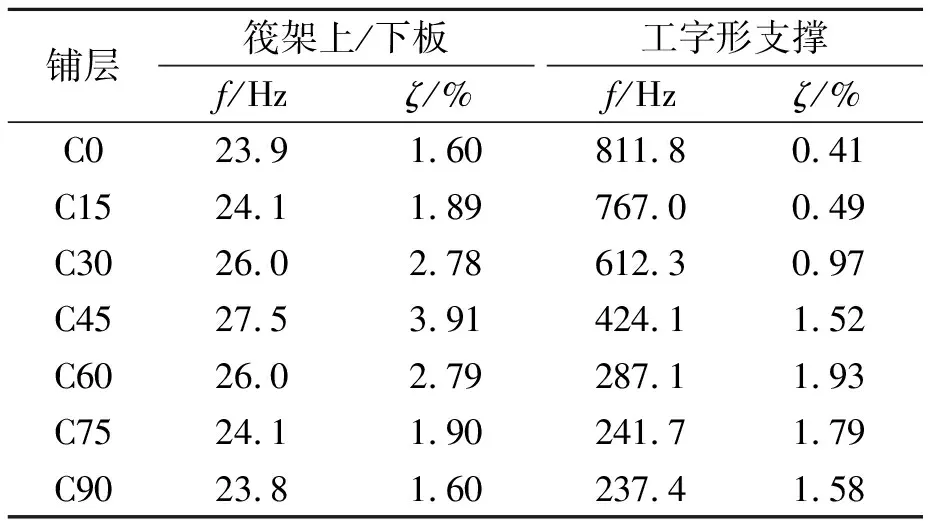
表3 组件一阶弯曲模态固有频率及阻尼比

图6 筏架上/下板一阶弯曲固有频率及阻尼比

图7 工字形支撑一阶弯曲固有频率及阻尼比
从图6可知,筏架上/下板一阶弯曲模态固有频率与阻尼比的变化趋势一致,在0~45°逐渐上升,在45°~90°逐渐下降,并呈沿45°对称分布。其一阶弯曲模态固有频率与层合板最小弯曲刚度min{D11,D22}变化趋势相同,说明在弯曲刚度较小方向上的模态首先被激励;阻尼比与两个方向上弯曲刚度的比值min{D11,D22}/max{D11,D22}趋势相同,这是由于两个方向刚度均衡后更容易发生剪切变形,而12方向的阻尼损耗因子要远大于11和22方向。
从图7可知,工字形支撑一阶弯曲模态固有频率与阻尼比的变化趋势基本相反,这是由于该弯曲模态主要受腹板支撑方向的弯曲刚度D11影响,随着D11逐渐减小,该模态更容易被低频信号激励。同时,工字形支撑的阻尼比在0~60°持续增加并达到最大值,60°~90°开始减小,并非随着主方向弯曲刚度的持续减小而持续增大,这说明更容易发生弯曲变形并不一定意味着有更高的能量耗散能力,这对设计结构时平衡刚度和阻尼性能有一定的指导意义。
3 筏架减振性能分析
3.1 隔振系统有限元模型
建立浮筏隔振系统有限元模型,如图8所示,其中筏架上/下板尺寸为700×700×4.8 mm;工字形支撑高70 mm,腹板厚4.8 mm;电机质量7.4 kg,位于筏架上板中央模拟单设备激励,简化为等质量块,材料为45#钢,密度7 860 kg/m3,杨氏模量为210 GPa,泊松比为0.3,阻尼比取0.002。基座材料为45#钢,其下表面连接区域为全约束。电机与筏架上板通过4个BE-25型号橡胶隔振器连接,其X、Y、Z向刚度分别为100 N/mm、240 N/mm、92 N/mm,阻尼比为0.07;筏架下板与基座通过4个BE-60型号橡胶隔振器连接,其X、Y、Z向刚度分别为240 N/mm、580 N/mm、220 N/mm,阻尼比为0.07,模型中各铺层下的CFRP组件阻尼比采用表3中的计算结果。

图8 隔振系统有限元模型
设置参考点与电机耦合,施加10 N竖直向下的集中载荷模拟激振力,扫频频率范围设置为0~200 Hz。
通过加速度振级L来评价筏架各测点处的振动强弱,计算公式为:
L=20lg(|a|/aref)
(5)
式中:aref为加速度信号参考值,取10-6m/s2;a为加速度。
通过加速度振级落差来评价各测点之间的振动衰减,计算公式为:
LD=La-Lb
(6)
式中:LD为振级落差,La、Lb分别为输入、输出端加速度振级。
输入测点设置在电机与上层隔振器的连接点上,输出测点设置在基座与下层隔振器的连接点上,如图9所示。
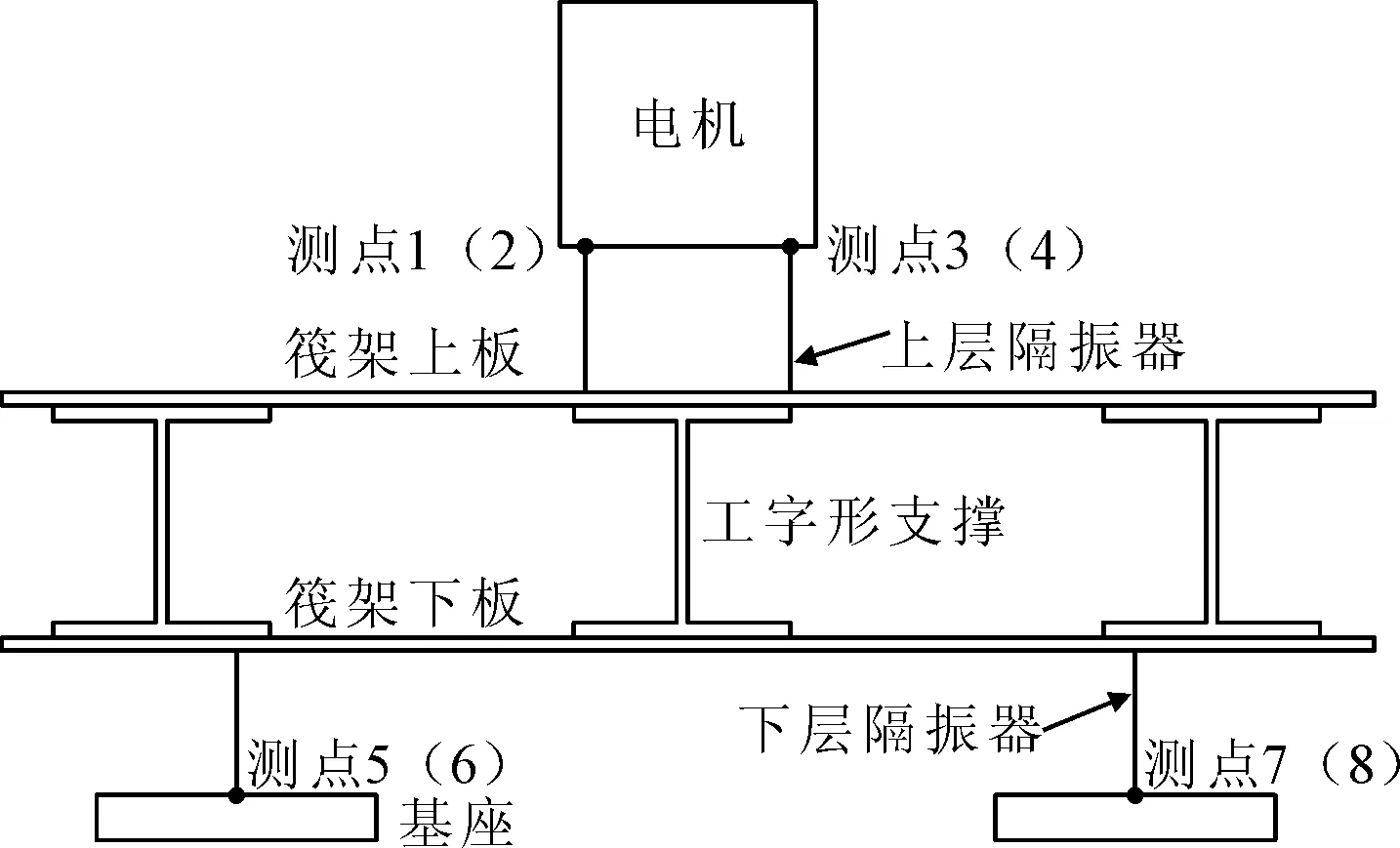
图9 加速度测点分布
3.2 CFRP筏架减振性能分析
分别仿真计算表4中9组CFRP筏架组件铺层方案的减振性能,表4中以X-X-X的形式分别表示筏架上板、工字形中间支撑、筏架下板的铺层设计,其中C0、C45、C90统称为N。

表4 CFRP筏架组件铺层方案
9组CFRP筏架谐响应分析结果如图10~图12所示。

图10 C0-N-C0组振级落差

图11 C45-N-C45组振级落差

图12 C90-N-C90组振级落差
图10~图12分别为筏架C0-N-C0、C45-N-C45、C90-N-C90铺层下隔振系统的振级落差。各自独立来看,在高频段(100~200 Hz)工字形支撑为C60、C90组的减振效果相对较好,结合表1说明高频段工字形支撑的阻尼比越大,减振效果越好。
横向对比图10~图12,在一阶共振频率处附近,C0-N-C0、C90-N-C90组的振级落差在100 dB左右,C45-N-C45明显减小,在90 dB左右,结合表1说明筏架上/下板的各向异性越明显,最小弯曲刚度越小,减振效果越好。
在高频段,随着筏架上/下板铺层角度的增加,各组振级落差的差异越来越明显。这主要由于筏架上板的最小弯曲刚度方向从其铺层坐标系的2方向转为1方向,导致其受激振力后变形情况不同,进而导致工字形支撑所受的主要弯矩的方向发生改变。如图13和图14所示,C0-N-C0组工字形支撑所受主要弯矩为其铺层坐标系的绕3方向的弯矩,其腹板以3轴为中心轴的抗弯截面系数较大,结构抗弯刚度受铺层角度变化影响相对较小,表现为振级落差曲线十分相近;C90-N-C90组工字形支撑所受主要弯矩为绕2方向的弯矩,其腹板以2轴为中心轴的抗弯截面系数较小,结构抗弯刚度受铺层影响较大,振级落差曲线有明显区别。

图13 C0-N-C0铺层一阶共振模态及工字形支撑所受主要弯矩

图14 C90-N-C90铺层一阶共振模态及工字形支撑所受主要弯矩
综上所述,系统在低频段的振级落差主要受筏架上/下板的最小弯曲刚度影响,最小弯曲刚度越小,振级落差越大。高频段振级落差主要受工字形支撑的阻尼比影响,阻尼比越大减振效果越好,同时其载荷方向是影响材料阻尼作用发挥的重要因素,在所受弯矩下越容易发生弯曲变形,阻尼减振效果越明显。
3.3 CFRP-钢质组合式筏架减振性能分析
分别将筏架上板、工字形支撑、筏架下板替换为钢质组件,沿用3.2节中的编号,被替换为钢质的组件统一用“M”表示。CFRP-钢质组合式筏架与CFRP筏架、全钢质筏架的谐响应分析结果如图15~图23所示。
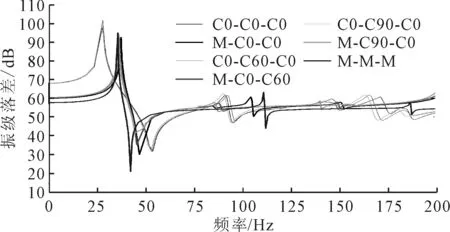
图15 M-N-C0筏架振级落差对比

图16 M-N-C45筏架振级落差对比
图15~图17为筏架上板替换为钢质的仿真结果,通过比较可知,在一阶共振频率之前CFRP-钢质组合式筏架各组振级落差相较于CFRP筏架均明显下降5~10 dB,略优于全钢质筏架,结合3.2中的结论进一步说明CFRP筏架上板在低频段的减振效果。在高频段含有CFRP组件的筏架系统减振效果要好于全钢质筏架,同时该组CFRP-钢质组合式筏架一阶共振频率与全钢质筏架相当。

图17 M-N-C90筏架振级落差对比
图18~图20为工字形支撑替换为钢质的仿真结果,通过比较可知,在一阶共振频率附近CFRP-钢质组合式筏架各组振级落差与CFRP筏架无明显变化。横向比较来看,在高频段C90-M-C90组CFRP筏架减振效果相对较好,中间支撑的阻尼比性能得到发挥,结合3.2中的结论进一步说明高频段主要受工字形支撑阻尼比影响,同时该组CFRP-钢质组合式筏架一阶共振频率与CFRP筏架相当。

图18 C0-M -C0筏架振级落差对比

图19 C45-M -C45筏架振级落差对比
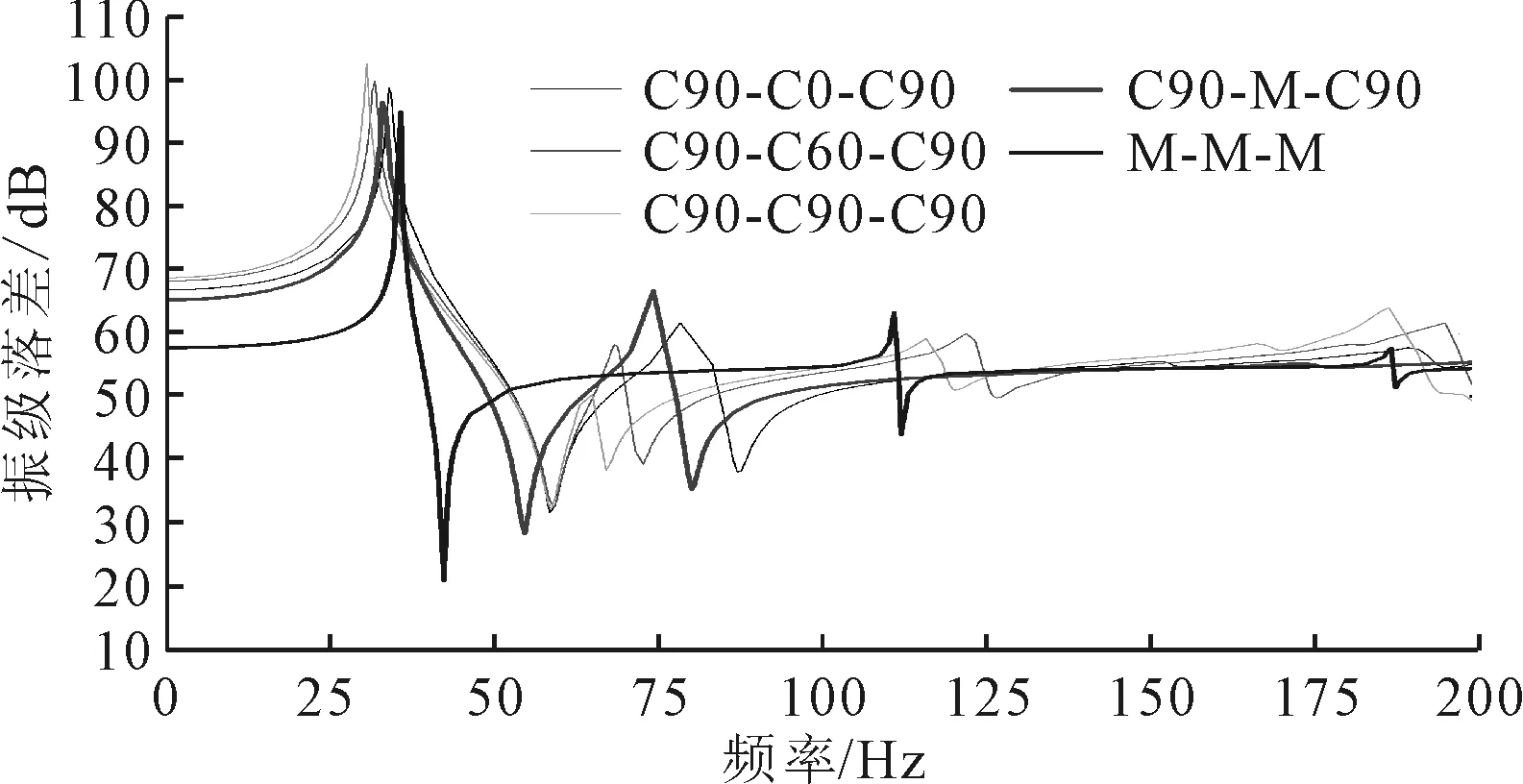
图20 C90-M -C90筏架振级落差对比
图21~图23为筏架下板替换为钢质的仿真结果,通过比较可知,在一阶共振频率之前CFRP-钢质组合式筏架各组振级落差相较于CFRP筏架均下降4~8 dB,明显优于全钢质筏架,结合3.2中的结论进一步说明CFRP筏架下板在低频段的减振效果;在高频段含有CFRP组件的筏架系统减振效果要好于全钢质筏架,同时该组CFRP-钢质组合式筏架一阶共振频率最小。

图21 C0-N-M筏架振级落差对比
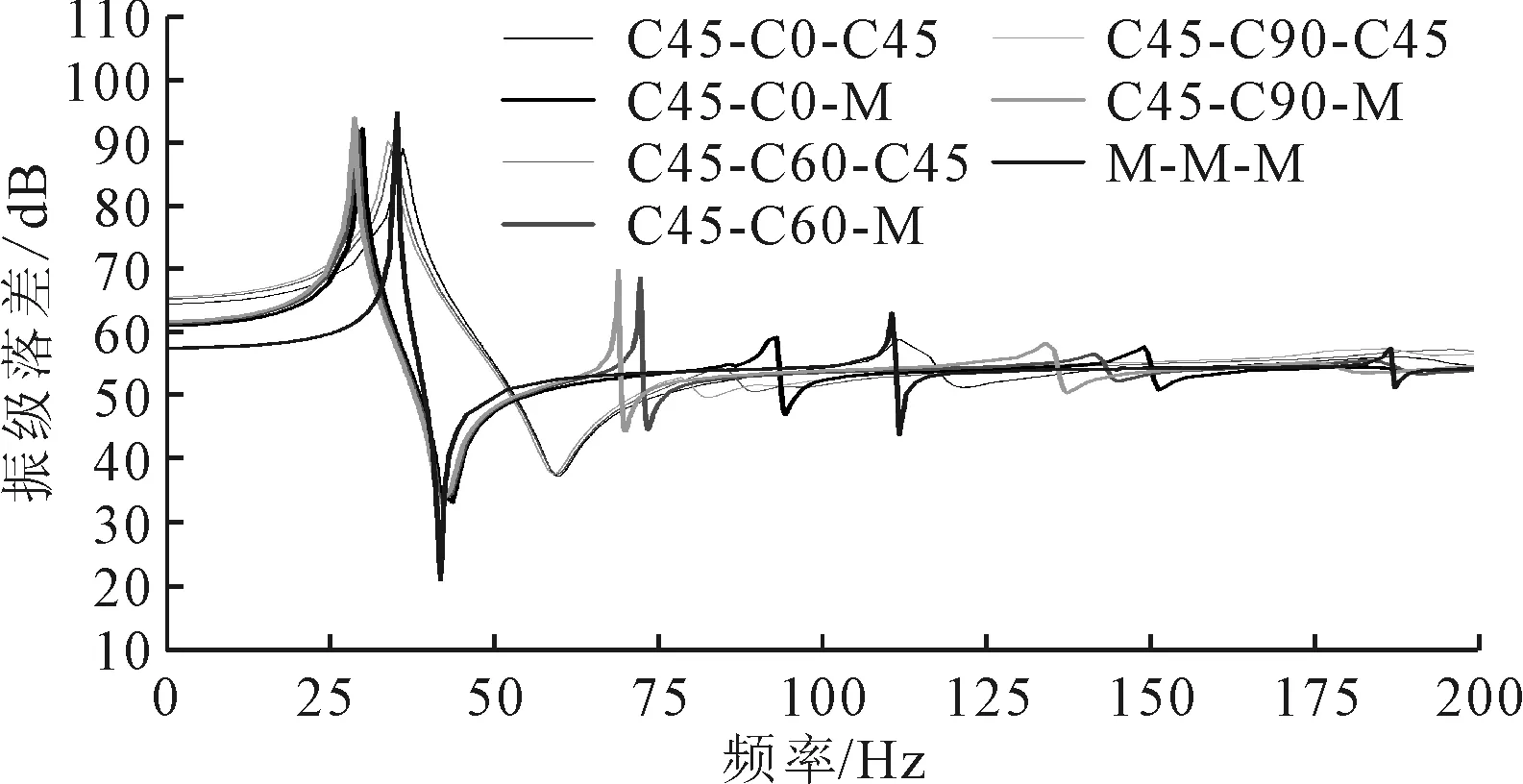
图22 C45-N-M筏架振级落差对比
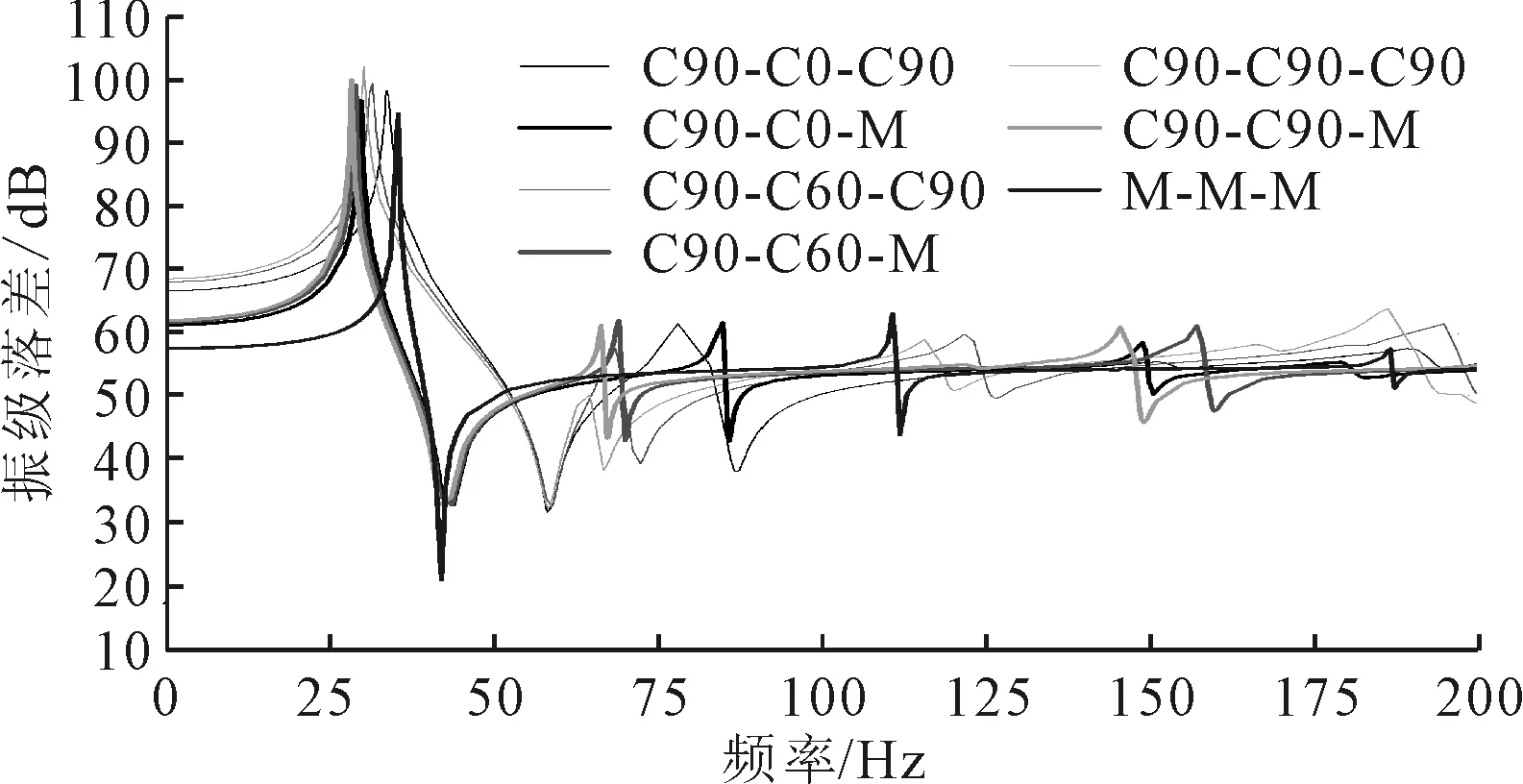
图23 C90-N-M筏架振级落差对比
4 结论
(1)CFRP筏架不同组件影响减振效果的性能参数不同,筏架上/下板影响参数主要是最小弯曲刚度,工字形支撑影响参数主要是阻尼比。
(2)CFRP筏架上/下板主要在低频段具有明显的减振效果,较全钢质筏架减振效果提升约4~10 dB。
(3)CFRP工字形支撑主要在高频段起到减振效果,并与其载荷方向、抗弯截面系数相关,抗弯截面系数小的方向抗弯刚度易受铺层角度影响,阻尼减振性能体现更加突出。
(4)含有CFRP组件的筏架在低频段普遍比全钢质筏架具有更好的减振性能;钢质组件能明显改变系统的一阶共振频率。
