基于WOA和LA的安全路由协议优化设计
2021-12-23吴明芬
熊 英,吴明芬
(1.江门开放大学 信息技术部,广东 江门 529000;2.五邑大学 智能制造学部,广东 江门 529000)
0 引 言
移动自组网(mobile ad hoc network,MANET)[1,2]基础设施的缺失降低了恶意行为检测效率,要求数据传输应尽可能选择高安全性链路,安全路由协议优化问题随之产生。
提高路由协议安全性可通过优化协议参数实现。文献[3]以节点移动度为指标,设计多点延时改进机制,提出OLSR安全优化协议,丢包率降低,但链路负载和电池剩余能量等性能下降。文献[4]为规避NP-C(nondetermi-nistic polynomial completeness)问题,提出基于信任度的服务质量路由(trust-based QoS routing,TQR)模型,丢包率和时延得到改善,但重传分组数急剧增加,吞吐量降低。文献[5]指出单指标优化模型的局限性,建立了时延、跳数、代价和可靠性等参量的多维目标函数,基于蚁群算法实现了NP-C寻优,但恒比特流(constant bit rate,CBR)丢包率较高。文献[6,7]引入能量参数,分析了丢包率、时延/抖动,但协议复杂度增加,约束条件有待改进。于是安全路由协议问题变为多维目标函数优化问题,后者广泛采用元启发优化算法解决多维目标函数NC-C问题[8-11]。其中基于种群优化算法的鲸鱼优化算法(whale optimization algorithm,WOA)通过模拟座头鲸猎物包围、气泡攻击/区域划分、猎物寻找/域内搜索、猎物击中等行为,实现全域螺旋搜索,被逐步用于安全路由协议的优化设计[12]。但文献[13]指出,在WOA探索阶段,低效的域划分和域内搜索机制降低了算法收敛速度及最优解的寻优效率。同时文献[14]提出的狮子算法(lion algorithm,LA)将搜索域一分为二(即male和female域),各域内并行搜索,通过领域防护和领域接管驱散过时解,搜索效率较高。将LA引入WOA搜索环节,可一定程度上改善WOA的运行效率和协议的性能。
为此本文定义能量、时延、链路生存时间等安全参数,设计多维目标安全路由协议模型,基于WOA和LA提出寻优算法LAWOA,并分析协议相关性能。
1 安全路由协议设计
在安全协议路径选择过程中,存在邻节点数或路径数量较大的情形,为降低运算量、计算时延和协议复杂度,WOA、TQR、LA等算法一般对其中前k条路径进行优选,本节同样采用该方法对路径优选。具体过程为:在给定一定拓扑结构的网络模型及多播收发节点的基础上,利用k-means算法从所有可用路径中优选出前k条可用路径,定义相关安全协议参数,设计与之对应的归一化目标函数,并利用优化算法迭代查找最优解,此时安全性最高(目标函数最优)的路径用于收发节点之间的数据传输,协议的安全性将会明显提升。值得注意的是,k-means算法是成熟度比较高的算法,因此该安全协议的关键问题在于安全参数的选取(文中采用信任度、能量、时延、链路维持时间、移动性5个指标)、目标函数的定义和优化迭代算法的设计等环节。安全协议工作流程如图1所示。

图1 安全协议整体框架
2 参数选择
如前所述,安全路由协议相关参数包括信任度、节点能量、链路维持时间、时延、节点距离/移动性等,本节给出5种参数的定量表达式,为多维目标函数的建立和求解提供参数基础。
2.1 信任度
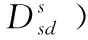
(1)
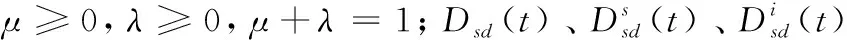
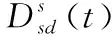
(2)

(3)
式中:N表示任意时刻节点的邻节点数目。
将式(2)和式(3)代入式(1)即可获得节点之间的信任度值,但其值是静态的,与MANET节点动态性存在一定差距。为降低误差,每次迭代后均采用移动平均模型[16]加权更新,即
(4)
加权因子ε∈(0,1),用于实现t和t+1时刻信任度值的均衡。
2.2 能 量
MANET中所有节点均由电池供电,且电池剩余能量与通信时间成反比。当电池剩余能量低于数据收发能量阈值时,收发节点之间将随时中断,协议安全系数也降低,因此建立能量剩余模型用于节点状态监控,可提高协议安全性。在不考虑电池发热损耗的条件下,能量消耗用于数据分组的接收和发送,因此节点剩余能量等于初始能量与接收/发送分组所消耗能量的差值。令节点初始能量为最大归一化值Pfull=1,任意时刻t剩余能量Pres(t)表示为
Pres(t)=Pres(t-1)-PTx·NTx(t-1)-PRx·NRx(t-1)
(5)
首次开机加电时Pres(t)=Pfull;PTx、PRx为发送、接收单位比特所需能量,NTx(t-1)、NRx(t-1)为对应的比特数目。对于PTx和PRx而言,考虑超短波通信频段,当忽略发热损耗时,二者归一化值约为
PTx=3PRx=0.03
(6)
由于Pres(t)大于一定阈值Pthrehold即可维持数据收发,因此为简化计算,对Pres(t)做二值化处理,即

(7)
2.3 链路维持时间
在MANET分组传输过程中,链路维持时间小于信息传输所需时间时,将导致节点之间通信中断,链路修复周期内数据分组将丢弃。因此选择的链路生存时间越长,路由协议越安全。链路生存时间与节点的移动性、方向性、电磁特性等相关。考虑坐标分别为(xs,ys)、(xd,yd)的节点ns和nd,归一化链路维持时间定义为
(8)
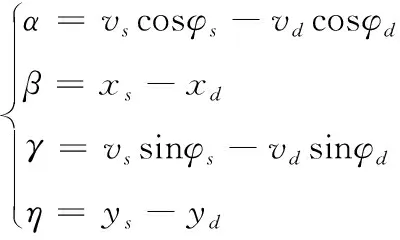
(9)
其中,TM为链路维持时间,R为电磁波覆盖范围,vs、vd、φs、φd分别为ns和nd对应的运动速度和方向角。
2.4 时 延
任何分组传输都存在时延,时延越大,恶意节点成功检测到正常用户并实施攻击的概率越高,且突发噪声对通信链路的影响也越大,因此时延同样可以作为衡量协议安全性的重要参数。时延包括传输时延、处理时延、排队时延和传播时延等。在此假设MANET终端节点配置及数据随机产生函数完全相同,那么时延由传播时延决定,其值与跳数相关。任意时刻t归一化时延Rsd(t)定义为传输路径中节点的跳数(或个数)NPath(i)与所有可用路径中节点总数的比值,即
(10)
式中:P为t时刻路径的总数,其值由路由表数据统计获得。同时为降低统计误差,利用移动平均模型对其加权平均,即
R′sd(t+1)=τRsd(t)+(1-τ)Rsd(t+1)
(11)
τ为加权系数,且τ∈(0,1)。
2.5 移动性
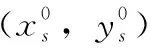
(12)
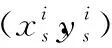
(13)
3 目标函数建立及优化算法设计
本节在信任度、能量、时延、链路维持时间、移动性等服务质量参数基础上,定义多维目标优化函数及最优解形式,并基于LA和WOA设计与之对应的优化迭代搜索算法。
3.1 最优解形式
最优解编码形式是算法迭代搜索过程的重要参数,也是译码获得最优解的重要方法。由于安全协议目的是获取源节点S到目的节点D之间的最佳路径,等价于确定最值问题,因此求解过程可转化为二分查找问题。理论上,对于MANET任意节点而言,所有节点都可能成为其邻节点,对应路由数目应等于网络节点数。而在协议实际运行过程中,任意微小时间间隔内(路由更新时间为ms级),低速运行(如1 m/s)环境路由表中存储的路径数(记为k)可视为常数,且其值远小于网络节点数。因此为简化计算,在所有S到D的直连和中继路径中,基于k-means按优先级顺序优选出前k条路径,每条路径用pi表示,则k条路径集合可记为P={p1,p2,…,pk},于是路径编号集合np={1,2,…,k}可视为S到D对应的路径函数解,从p1~pk中确定使目标函数达到最值的解即为最优解。
3.2 多维目标函数定义
目标函数是确定最优路径的关键。如前所述,信任度、能量、时延、链路维持时间和移动性等指标均影响着协议的安全性,因此协议设计中应兼顾指标之间的均衡,于是目标函数需由5个指标共同确定,建立目标函数与各指标之间的联合表达式。例如信任度越大,链路选择概率越高,协议安全系数越高,目标函数值也越大。同理可确定能量、时延、链路维持时间和移动性与安全协议的关系,于是归一化目标函数定义为
(14)
式中:dthreshold、M分别表示协议允许距离最大值、链路维持时间最大值,二者为常数。使式(14)获得最大值的路径即为最优路径,于是问题转化为目标函数的优化求解。
3.3 优化算法设计
3.3.1 优化算法执行流程
WOA算法由围猎(encircling prey,EP)、攻击/开发(bubble-net attack or exploitation phase,BA)、搜索/探测(search for prey or exploration phase,SP)3个环节构成。EP实现本地猎物识别及包围功能,BA实现目标的靠近,SP实现目标猎物的搜索。其中SP环节决定了WOA算法迭代的方向和搜索范围,算法的快慢直接影响着WOA的效率。如前所述,WOA算法已被广泛用于多参数优化设计中,但算法在SP更新环节冗余度较高,搜索范围随机性大、重复率高,使其收敛速度较慢。对于MANET而言,随着节点的移动,拓扑结构和链路状态均随时间变化,过慢的收敛速度降低了算法的精度,最佳路径误差也随之增加。不难理解,提高WOA算法的收敛速度将一定程度上提高协议的运行效率和安全路径的精度。同时LA算法模拟狮子领域更迭、接管、挖掘、荣誉等群体行为,将群体一分为二(male和female两类)并行种群更新,算法迭代及搜索效率提高,可很大程度上弥补WOA算法的不足。因此将LA算法融入WOA算法迭代过程能够兼顾WOA多维目标函数搜索的适用性和LA算法的高效性。结合WOA和LA算法流程,新算法对应工作流程如图2所示。
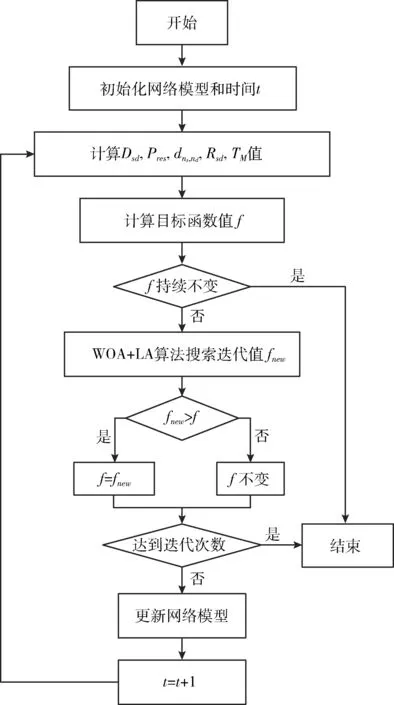
图2 优化算法流程
在t=0时刻,初始网络模型给定后,可根据式(4)、式(7)、式(8)、式(11)、式(13)分别计算出Dsd、Pres、TM、Rsd、dns,nd等参数值,代入式(14)可计算无量纲目标函数f值,如果f值长时间保持不变(如迭代1000次f值不变),算法迭代终止,并将该值赋予最优解,退出搜索;否则基于WOA和LA算法在群体中迭代搜索最优值,在任意迭代过程中,如果搜索所得目标函数值fnew>f,表示产生了更优质的解,将其存储在f值中,否则f值保持不变;同时判断搜索次数是否达到迭代次数上限,如果是,则表示搜索过程结束,否则继续进行下一轮搜索,直至函数值最优。此时优化算法的关键在于基于WOA和LA算法搜索fnew值。
3.3.2 基于WOA和LA算法的搜索算法设计
基于WOA和LA算法思想,在此将新算法分为初始化、适应性评估、位置估计/更新、最优代理确定和结束5个阶段执行。
(1)初始化
随机生成包含n个值的解向量Fj,每个Fj记为
Fj={f1,f2,…,fn}
(15)
fj为表示第j条路径。与此同时,初始化系数向量U和L,用于WOA算法的迭代,二者分别由式(16)、式(17)确定
U=2db-d
(16)
L=2d
(17)
其中,d从2向0线性递减,b为[0,1]内的随机数。
(2)目标函数估值
根据式(14)计算目标函数值。值得注意的是,初始化后,群体并不知道目标值/猎物的相关位置信息,因此目标函数值为空,那么此时计算获得的目标函数值及其群体将作为最佳代理和最优值存储,为下一步迭代使用。
(3)位置估计与更新
最佳代理确定后,WOA算法模拟虎头鲸围猎行为(包围猎物、气泡攻击、寻找目标)搜索最优值,首先确定距离向量Q为
Q=|L·F*(i)-F(i)|
(18)
式中:F*(i)为最佳代理位置向量,此时根据WOA包围猎物更新规则,第i+1次迭代值可表示为
F(i+1)=F*(i)-L·Q
(19)
在WOA攻击环节,采用螺旋气泡攻击技术更新位置信息,该技术取决于代理与猎物之间的距离向量,螺旋函数表示为
F(i+1)=Q′·ehl·cos(2πl)+F*(i)
(20)
式中:Q′=|F*(i)-F(i)|表示最佳代理与目标猎物的距离,其值越小,表示越接近目标值;h表示指数螺旋函数的系数,决定螺旋函数的阶数;l为[0,1]内的随机数。为了改进搜索空间,加快算法执行效率,搜索更新过程引入LA算法,根据LA算法定义,更新规则为
F(i+1)=F(i)+(0.1q2-0.05)(F*(i)-q1F(i))
(21)
由式(19)可知
F*(i)=F(i+1)+L·Q
(22)
将式(22)代入式(21)可得
F(i+1)=F(i)+(0.1q2-0.05)(F(i+1)+L·Q-q1F(i))=
F(i)+0.1q2F(i+1)+0.1q2L·Q-0.1q2q1F(i)-0.05F(i+1)-0.05L·Q+0.05q1F(i)=F(i)(1-0.1q2q1+0.05q1)+
F(i+1)(0.1q2-0.05)+L·Q(0.1q2-0.05)
合并同类项
F(i+1)(1-0.1q2+0.05)=F(i)(1-0.1q2q1+0.05q1)+L·Q(0.1q2-0.05)
则
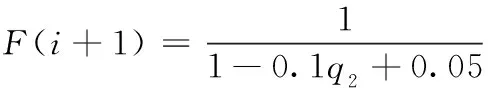
(23)
式中:F(i)、F(i+1)分别为位置更新后当前迭代和下次迭代位置向量。
(4)确定最优代理
当位置信息确定后,算法通过系数更新向量和距离向量生成下一代群体对应路径集。在此基础上,基于目标函数计算相应值,且目标函数仅保存目标函数最大值,并递增迭代变量。
(5)结束
算法重复过程(2)~过程(4),直至满足以下两个条件之一时退出:目标函数值长期不变;迭代次数达到最大值。
综上,基于WOA和LA的新算法执行流程如图3所示。
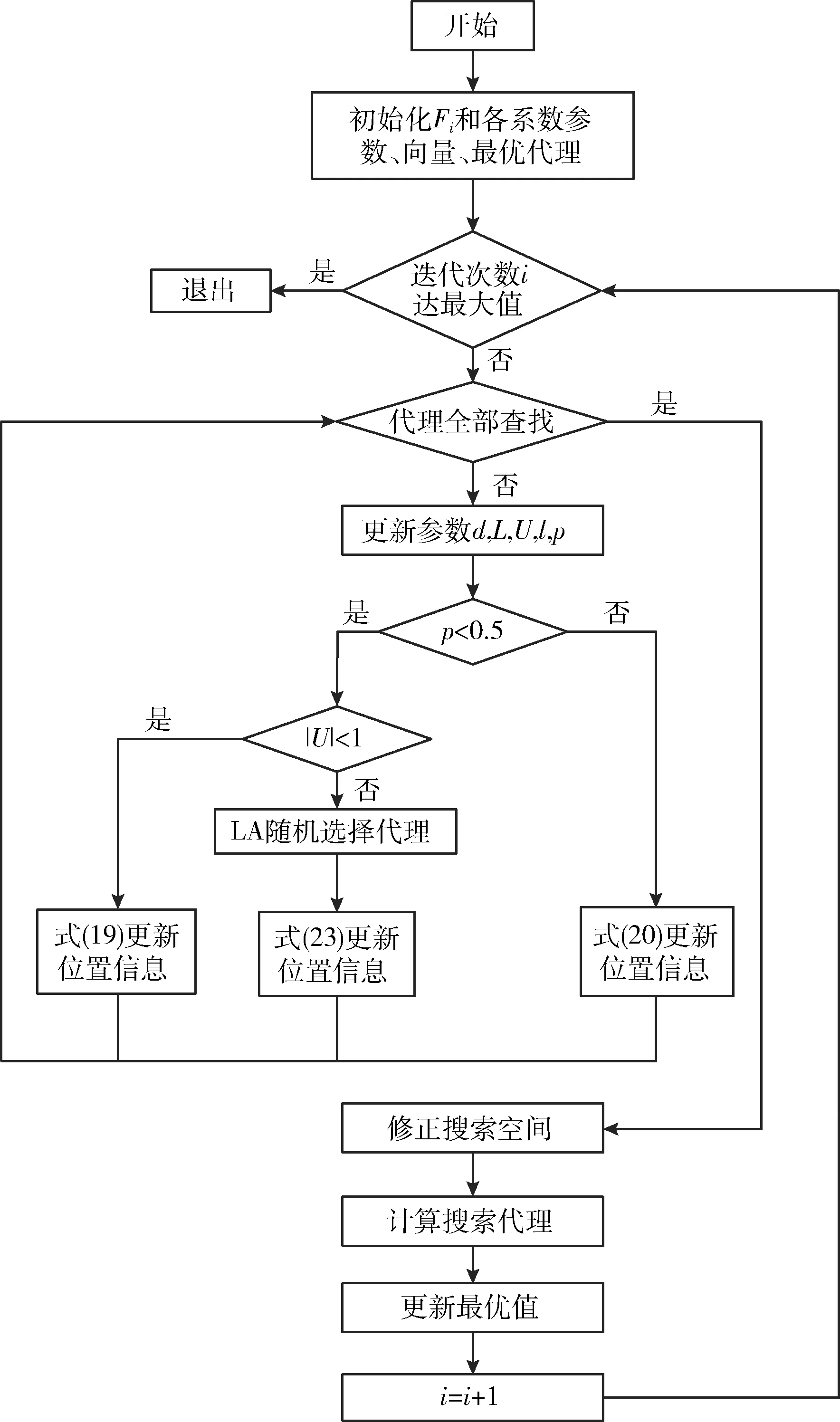
图3 迭代搜索流程
4 结果分析
4.1 实验环境
算法测试在Linux环境下进行,所需实验环境包括硬件、软件和模型参数3个方面,硬件为测试提供算力支撑,软件涵盖了测试所需的系统、网络仿真器(network simulator,NS)、图形显示、协议(内置WOA等算法,在此名称由算法替代)等方面,模型参数用于确保各算法在仿实际环境中的顺利执行,仿真过程涉及的主要实验参数设置见表1,恶意节点在t=0.5时刻随机选择网络节点开始运行。

表1 仿真参数设置
4.2 性能指标
就协议安全性而言,需考量吞吐量和丢包率两个重要指标。同时为衡量算法运行效率,需增加时间复杂度等性能分析。其中吞吐量为单位时间内数据分组的总数,单位为字节/s(或b/s),用Throughput表示;丢包率是指未接收分组与发送分组的比值,为无量纲参数,用Loss表示;时间复杂度可用算法收敛时间定性表征。为此Throughput和Loss表达式分别为
(24)
(25)
4.3 仿真结果
为了更好地说明LAWOA算法的性能,在此对WOA、TQR和LAWOA对应的Throughput、Loss、算法运行时间结果进行对比分析。图4为节点分布图,图5、图6分别为Throughput曲线和Loss曲线,表2为算法收敛时间。
从图5可看出,吞吐量与节点数目成正比,与恶意节点比例成反比。随着恶意节点(t=0.5)的加入,吞吐量迅速递减,当达到一定时间(50节点、100节点对应t=7、t=8时刻)后,网络趋于稳定,吞吐量保持不变,且恶意节点比例越高,吞吐量下降速率越快。同时LAWOA对应 协议吞吐量明显高于WOA与TQR算法(50节点、100节点分别高约300字节/s、400字节/s)。原因在于:一是当恶意节点执行攻击行为后,部分网络带宽用于传输恶意节点分组,使得用于传输数据分组的带宽受限,吞吐量降低,且恶意节点数越多,带宽浪费越严重,吞吐量降低越快,到达一定程度后,网络将出现拥塞,节点根据退避算法和重发机制强制推迟分组发送,正常节点和恶意节点处于竞争发送分组的稳定状态;二是LAWOA对应协议收敛速度比WOA和TQR快,有效降低了恶意节点的作用时间,对应吞吐量得到明显提升。
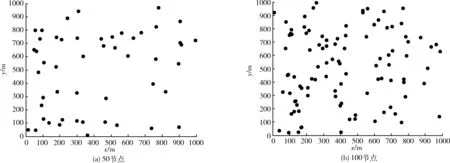
图4 节点分布


图5 吞吐量曲线
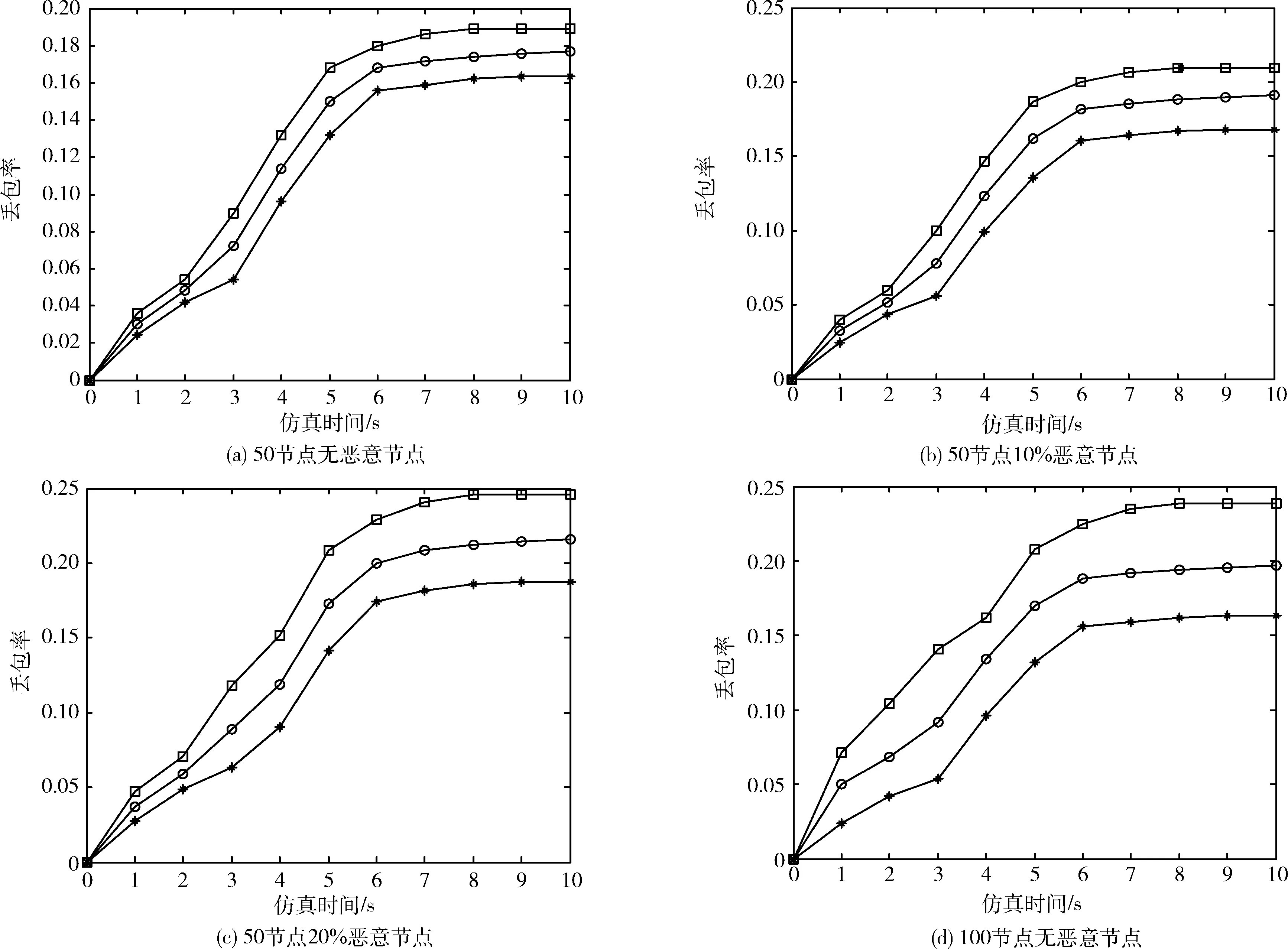
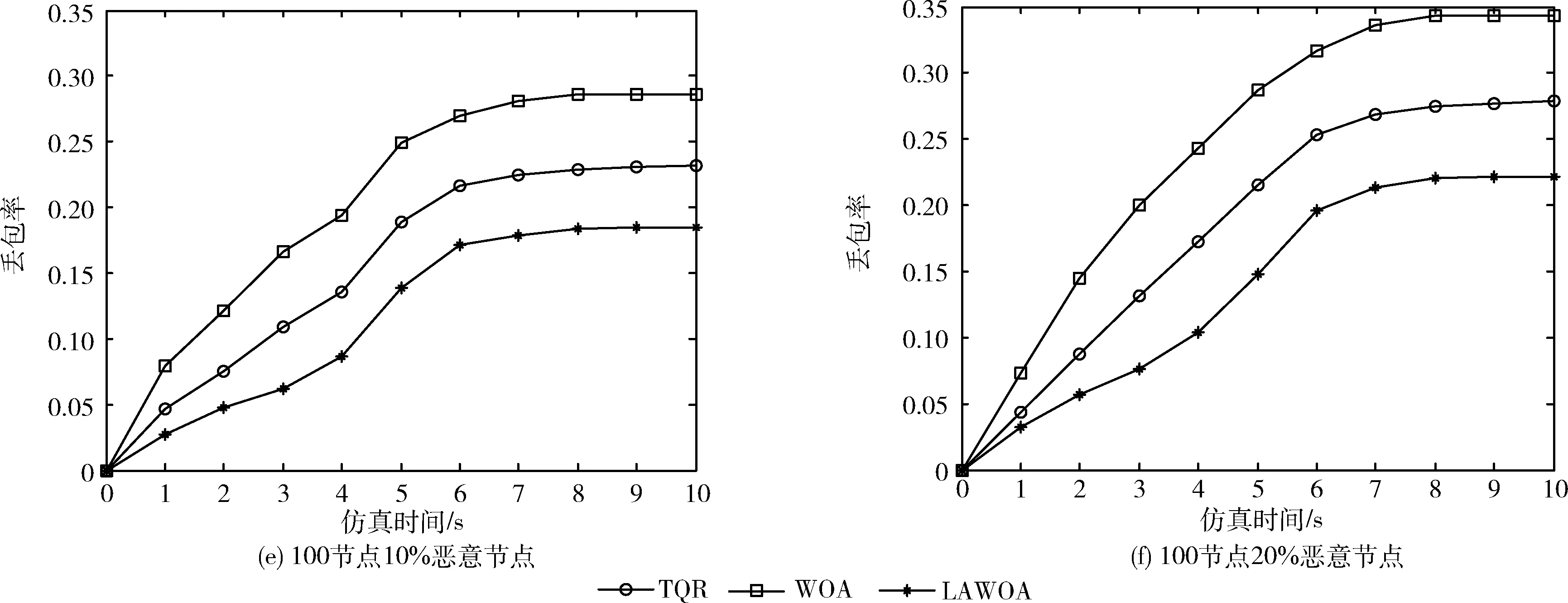
图6 丢包率曲线
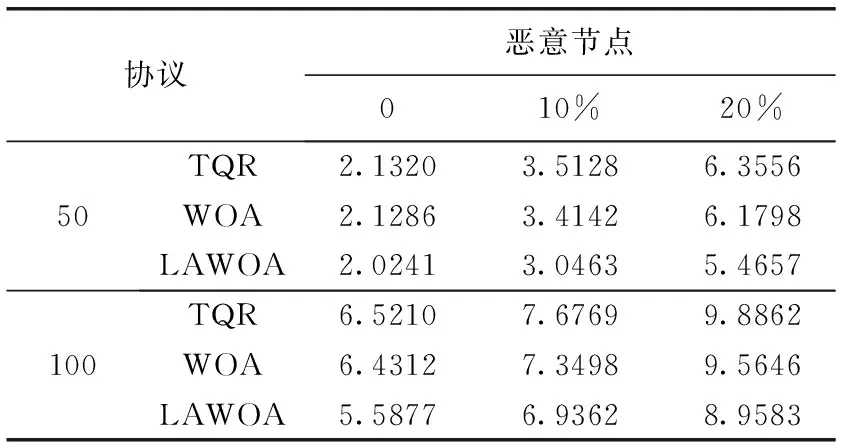
表2 算法收敛时间/s
从图6可以看出,丢包率与节点数、恶意节点比例均成正比,且随着恶意节点的加入,丢包率迅速增加,达到一定时间后趋于平稳,与TQR、WOA算法对应协议相比,LAWOA算法丢包率降低了10%~12%。原因在于:一是恶意节点导致网络拥塞,而且分组碰撞概率增加,使得丢包率增加;二是LAWOA算法以较高效率收敛到最佳路径,使得节点检测到路径变差时,可迅速切换到最佳路径,分组丢弃概率降低,从而网络整体丢包率降低。
从表2可看出,总体而言,随着恶意节点比例的增加,收敛时间变长,速度变慢。原因在于,恶意节点的加入导致MANET节点对正常/恶意节点产生误判,节点需重新发送测试分组以确定节点类型,判定时间延长,路径选择时间增加,算法收敛速度降低。同理,网络节点数越多,算法对节点类型的判定时间越长,同时节点获得网络拓扑信息的时间变长,路径选择复杂度增加,算法收敛速度降低。与图5、图6相比,Throughput和Loss稳定点并不是收敛点,可能原因在于其它链路综合Throughput和Loss与平均值是一致的,获得最优安全路径后保持性能指标恒定。此外恶意节点比例0~20%递增时,LAWOA收敛时间比TQR和WOA对应值低5%~15%。其原因在于LA算法将搜索域分为male和female两部分,各部分能够分别识别各自域内的恶意节点,但并非速率减半,因为LA算法还要实现域间整合,同样需要一定时间,因此收敛时间提升,并非效率加倍。
5 结束语
本文针对路由协议安全问题,提出一种安全路由协议模型,引入5种安全定量参数,设计对应的多维目标优化函数,并基于WOA和LA提出相应的优化算法,通过吞吐量和丢包率验证了优化模型的性能。但是仍存在以下不足:①网络规模有待增加;②高速移动环境中的协议安全性能尚未验证;③网络长期特性尚未讨论;④最优路径转换时间尚缺少定量分析。后期将对以上问题展开进一步研究。
