距离度量法聚类的无线传感器网络路由算法
2021-12-23方旺盛万良香胡中栋
方旺盛,万良香,胡中栋
(江西理工大学 信息工程学院,江西 赣州 341000)
0 引 言
无线传感器网络(wireless sensor networks,WSNs)[1]一直作为重要的工具,广泛运用于各类场合中,例如医疗康复[2]、野外战场环境监测、国家边境防御装备等。由于传感器节点(Node)部署后一般不可移动且难以蓄电,因此如何节省网络能耗一直是研究的热点。分簇路由算法[3]与非层次路由算法相比较更节省能耗,所以分簇路由算法为当下研究重点。
文献[4]基于经典分簇路由LEACH协议算法思想上,提出了以节点与簇头及节点与基站的距离信息作为簇内节点是否与基站直接通信的判定条件,以节省网络能耗。文献[5]提出模糊逻辑算法改进簇头选取机制及簇群尺寸,以选取更合适的簇头。文献[6]基于EEUC协议,引入了能量因素和节点度以改进竞争半径及阈值的设定,最终提高网络执行效率。文献[7]提出了加权值应用于簇首节点阈值,提升簇头选取质量。文献[8]提出环状网络区域,以划分区域的方式改进数据传递效率,提高网络生命周期。文献[9]提出了将无线传感器网络划分为不同大小的圆环,以改善“热区”问题。文献[10]提出K-means算法与LEACH协议结合,以减少传输能耗。
以上算法大多都是基于LEACH模型进行的改进,虽分簇思想能够有效提高生命周期,以上文献也均有考虑到节点能量因素,或综合考虑能量因素和位置因素,但是对于网络簇群分布不均问题仍然没有很好的改善。
因此,本文基于LEACH协议的思想上,为改善网络簇群分布不均问题,提出DMBC(distance measurement method based clustering algorithm for wireless sensor network)算法,该算法的主要思想是利用节点间距离作为重要指标改进K-means算法,使得簇群分布位置更加均匀,再利用节点的能量特性、位置特性优化每个簇群簇首选择,最终延长WSNs网络生命周期。
1 相关模型
1.1 系统模型
本文假定所有节点服从均匀分布且一旦部署后不可移动,其它具体特征如下:①Sink节点有且仅有一个,所有节点位置N(Xi,Yi)已知且不可移动;②每一个节点有相同的初始能量Eo;③部署节点可根据接收到信息的信号强度计算出发送节点到接收节点的距离;④每一个节点有唯一的标识号i,(i=1,2,…,N);⑤假定各节点均可相互通信,且所有节点均可与Sink节点直接通信;⑥所有节点均具备融合数据的能力。
1.2 无线通信能耗模型
网络节点在无线通信过程使用的能耗模型采用与文献[11]相同的无线通信模型,将l比特数据传输至距离d处位置时所需要的能耗公式如下
(1)
式中:Eelec表示发射模块在电路中消耗的能量,传输距离存在阈值d0作为能耗分界线,其计算式如下
(2)
当传输距离d小于阈值d0时,网络在传输数据的过程中采用自由空间模型;否则网络在传输数据的过程中采用多路径衰减模型,εfs、εmp分别是两模型中功率放大所需要消耗的能量。
1.3 数据融合模型
分簇路由协议中,数据融合技术被采用于减少传输能耗,即当簇首节点接收到簇内成员传输的数据具有相关性时,簇首则将簇内成员发送的信息量压缩为lbits,此时节点对数据融合所需能耗EDA由式(3)计算所得
EDA(l)=l*5nJ/bit
(3)
2 DMBC路由协议算法
LEACH协议的网络聚簇效果是和簇头选取过程共同完成的,但簇头选取机制考虑因素单一,最终成簇效果不佳,簇群分布不均。因此,本文将网络聚簇过程和簇头选取过程分开进行,先将网络划分成簇,而后在划分好的簇内选取合适的簇首节点。聚簇过程是利用改进的K-means算法模型获得,而簇首选举机制也加入了能量因素、位置因素,本文先将网络划分成簇可以使得网络保持较好的成簇效果,簇首选取机制的改进也能使得条件更佳的节点成为簇首。
2.1 K-means算法模型
K-means模型可以根据距离相似度将分布在网络的节点进行聚类,主要的步骤如下:
(1)在网络中随机选取K个节点作为初始的中心聚类节点,其它节点选取距离最近的中心聚类节点加入成簇,形成K个初始聚类。
(2)计算簇群的质心节点,每个簇群中与质心节点距离最小的节点成为新的中心聚类节点,而后所有节点加入最近的中心聚类节点产生簇群。
(3)算法迭代步骤(1)、步骤(2),直到标准测度函数开始收敛,或者是算法迭代多次直到中心聚类节点不再改变,得出聚类结果。
K-means算法比较简易,但是存在以下因素影响成簇效果:
(1)初始中心聚类节点随机选取,如果中心聚类节点过于集中会使得簇群过于集中,形成局部最优,导致成簇效果不佳。
(2)通过计算每个簇群的质心,距离质心最近的节点成为新的中心节点,簇群容易受个别“偏僻”节点影响,导致中心节点反而偏离大多数节点。
2.2 初始聚类中心点选取阶段优化
2.2.1 最优分簇
本文利用K-means算法思路进行聚类,初始需选取K个中心节点,K值根据文献[12]确定,其表达式为
(4)
式中:N为区域中节点个数,X为区域边长,dtoBS为基站至网络中节点的平均距离,εfs是自由空间信道模型的放大功率所需能耗,εmp是多径衰落信道模型的放大功率能耗。式中簇群个数K,随着节点个数N的投放量增加以及区域半径X扩大而增加,反之则减少;基站至节点距离dtoBS也是改变簇群个数的可变量,基站距离网络节点越近其簇群个数越多。
2.2.2 中心点选取过程
在K-means路由算法中,随机性的在网络中选取K个普通节点,根据质心位置变化迭代聚类,算法实现难度低,但是聚类过程中,容易陷入局部最优。当节点距离分布较近时,在迭代过程中,中心点可能过近甚至出现重合,两个簇群容易融合为一个簇群;当中心点距离分布远且在网络的各个方向分布,则成簇效果会更加合理。因此,针对以上的不足点,本文利用节点间最远距离作为K个初始中心节点选取的指标[13]。最大距离法的一般公式如下
{dis(d1,dk)*dis(d2,dk)*…*dis(dk-1,dk)≥ dis(d1,di)*dis(d2,di)*…*dis(dk-1,di),di≠d1,d2,…,dk-1}
(5)
式中:dk是网络中选取出来的中心聚类节点,di是网络中除已选中的中心聚类节点外的任意节点。
利用上述公式,中心点的优化选取过程如下:
(1)计算N个节点两两间的距离dis{i,j},找出满足:dis(d1,d2)≥dis(di,dj),(i,j=1,2,…,N)的两个节点,满足条件的两个节点成为初始簇群的中心聚类节点d1、d2。
(2)在剩余的N-2个节点中,找出节点距离条件满足:{dis(d1,d3)*dis(d2,d3)≥dis(d1,di)*dis(d2,di),(di≠d1,d2)}的节点成为中心聚类节点d3。
(3)在剩余的N-3个节点中,找到节点间距离条件满足{dis(d1,d4)*dis(d2,d4)*dis(d3,d4)≥dis(d1,di)*dis(d2,di)*dis(d3,di),(di≠d1,d2,d3)}满足条件的节点成为第4个中心聚类节点d4。
(4)依此类推,剩余K-4个中心节点根据上述方法得出。
2.3 节点距离度量法优化聚类
由于传统的聚类方法是计算簇群质心获取的,但是中心点容易受边界点影响,造成中心点偏移的状况。因此本文利用了节点距离度量法使得选取的中心点更加贴合簇群,其主要思想:
(1)首先每个节点根据和各中心节点距离,距离条件需满足:Min{Dis.center(a),(a=1,2,…,K)},其中Dis.center(a)表示节点和各中心聚类节点距离,节点加入簇群后分配簇群的唯一标识号a,簇群表示为Clustera,(a=1,2,…,K)。
(2)其次在每个Clustera簇群中,各节点计算与该簇内其余节点的距离(聚类节点除外),其距离表达式为Dis.nodei(a,j),(i,j∈Clustera,i,j≠dk),同时也计算上一轮中心聚类节点与该簇群节点的距离,表达式为:Dis.ctna(i),(i∈Clustera)。
(3)将Dis.nodei(a,j)、Dis.ctna(i)两距离进行比较,并利用该距离获取每个节点的邻居节点,其邻居节点获取表达式如下:Ni.Vic={Dis.nodei(a,j)≥Dis.ctna(i)|i,j∈Clustera},邻居节点集合中的节点数量越多,表示该节点在簇群中与各节点距离都比较近,因此将集合数目最大的节点更新为新的中心聚类节点,剩余节点重新加入中心节点成簇,直至算法迭代至簇群位置不再更新。
在上述的聚类思想中,聚类指标是节点间距离相似度,聚类中心根据距离相似度将符合标准的节点纳入所在簇群,最终聚类出簇大小和簇内成员相似的簇群。
2.4 簇头选举
普通节点仅需发送信息传输能耗,而簇首节点兼具收发任务,还需将簇内成员信息融合后再发送至Sink节点,因此簇头节点能量耗损最快,容易出现节点间能量差异大的现象,所以簇头选择至关重要。本文对簇头选举机制进行了改进,簇头阈值计算过程引入能量调节因子、质心因子、距离因子3个制约因素,以此改进阈值计算。
2.4.1 能量调节因子
网络划分成簇后,因根据距离相似度划分的簇群,位置分布不同的簇群其大小不一,并且随着信息传递,节点间接收和发送数据是能量不断消耗的过程,但每个簇群的能耗有所差异,因此能量调节因子定义如下
(6)
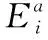
2.4.2 质心因子
簇头选举过程中,节点的位置要顾虑到大多数节点传递信息至簇头节点时的距离要较小,从而节省传输能耗。在此,每个节点定义了质心因子
(7)
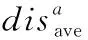
2.4.3 距离因子
簇头不仅仅需要接收簇内节点的信息,还需要将信息融合后传递至汇聚节点,所以仍然需要考虑节点至汇聚节点的距离,其距离因子定义为
(8)
式中:distoSink表示网络所有节点至汇聚节点的平均距离,disi表示节点i至汇聚节点的距离。
根据上述的能量、质心、距离因子,最终得出每个节点的阈值表达式如下
(9)
式中:β1、β2、β3为加权系数,β1表示能量因子加权系数;β2表示质心因子加权系数;β3表示距离因子加权系数。
式(9)结合式(6)可知,节点阈值T(n)与其剩余能量Eres相关,当节点剩余能量越高,阈值越大,成为簇头可能性越大,降低剩余能量少的节点成为簇头的可能;结合式(7)中,节点到质心距离distoc与簇内节点至质心距离成反比,即靠近质心的节点成为簇首节点的可能性越大;结合式(8)同理可知,簇内靠近汇聚节点的节点其阈值越高,节点成为簇头节点后可减少越多传输能耗。显然,算法综合了候选节点的剩余能量、地理位置优化簇头选举机制,从而避免能量低且位置不佳的节点成为簇首节点的可能性。
2.4.4 加权系数变化
在网络运行全过程中,所有节点不可移动,在网络初始运行阶段所有节点能量差异小,但能量在簇头选取过程中起重要作用,由此设定初始阶段能量加权系数β1=0.5,质心加权系数β2=0.25和距离加权系数β3=0.25。随着网络持续运行,全网总能耗不断下降,节点剩余能量成为选取簇头的关键,因此能量加权系数β1应随着总能量下降而增大,相对应的质心加权系数β2和距离加权系数β3相应减少,加权系数的增减与以下公式相关
(10)
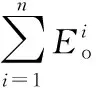
(1)当Rate(r)=0.2时,即全网总能量下降为初始总能量的20%时,能量加权系数β1增加0.1,对应的加权系数β2、β3均减少0.5,即β1=0.6,β2=0.2,β3=0.2。
(2)当Rate(r)=0.4时,即全网总能量下降为初始总能量的40%时,能量加权系数β1增加0.2,对应的加权系数β2、β3均减少0.1,即β1=0.7,β2=0.15,β3=0.15。
(3)当Rate(r)≥0.6时,即全网总能量下降为初始总能量的60%及以上时,能量加权系数β1增加0.3,对应的加权系数β2、β3均减少0.15,即β1=0.8,β2=0.1,β3=0.1。
根据上述步骤调节加权系数β1、β2、β3的值,可以使得簇头选取机制更加灵活,在网络初始运行阶段,节点间能量差异小,则重点考虑簇头节点的位置因素;当网络总剩余能量下降幅度开始大于初始总能量的20%时,则簇头节点选取的重要因素逐步放在节点剩余能量上;当网络总剩余能量仅有初始能量的60%时,此时部分节点能量仅剩初始能量的一半,网络也已经出现部分死亡节点,为均衡网络能耗簇头选举以剩余能量作为主要的参考因素。
3 实验仿真
此次实验使用MATLAB R2017B仿真软件对LEACH路由协议、LEACH-improved路由协议、DMBC路由协议进行仿真对比。仿真环境为100×100 m的正方形区域,假定区域内节点均匀分布。
表1为实验仿真所使用的基本参数,为对比协议效果,Sink节点设置于两个不同位置。
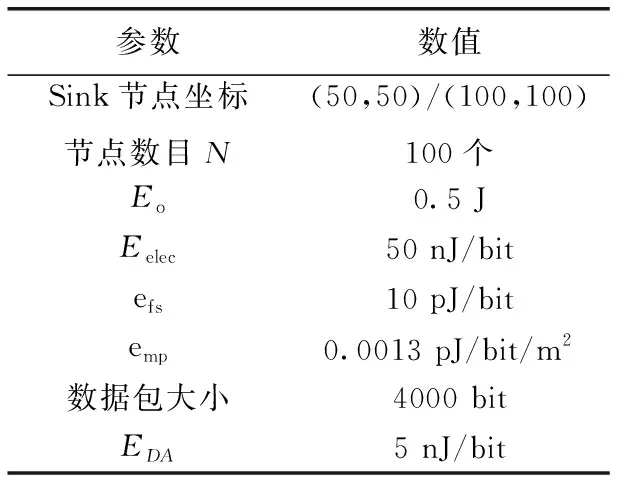
表1 仿真参数的设置
3.1 节点聚类仿真分析
设定在100 m×100 m的网络中,随即部署100个节点,对于LEACH路由协议算法中成簇效果的不均匀性以及随机性导致节点能耗过快问题,本文使用节点间距离相似度而改进的K-means算法聚类成簇,令聚类个数K=5。为避免不必要变量对实验效果产生影响,则对比算法中簇首个数尽量与本算法相等,设定LEACH协议的节点成为簇首的概率p=0.05,使得两协议簇头数目基本保持一致。
3.1.1 初始聚类仿真分析
本文利用最大距离法选取初始中心节点优化的K-means算法,其初始成簇效果如图1所示。
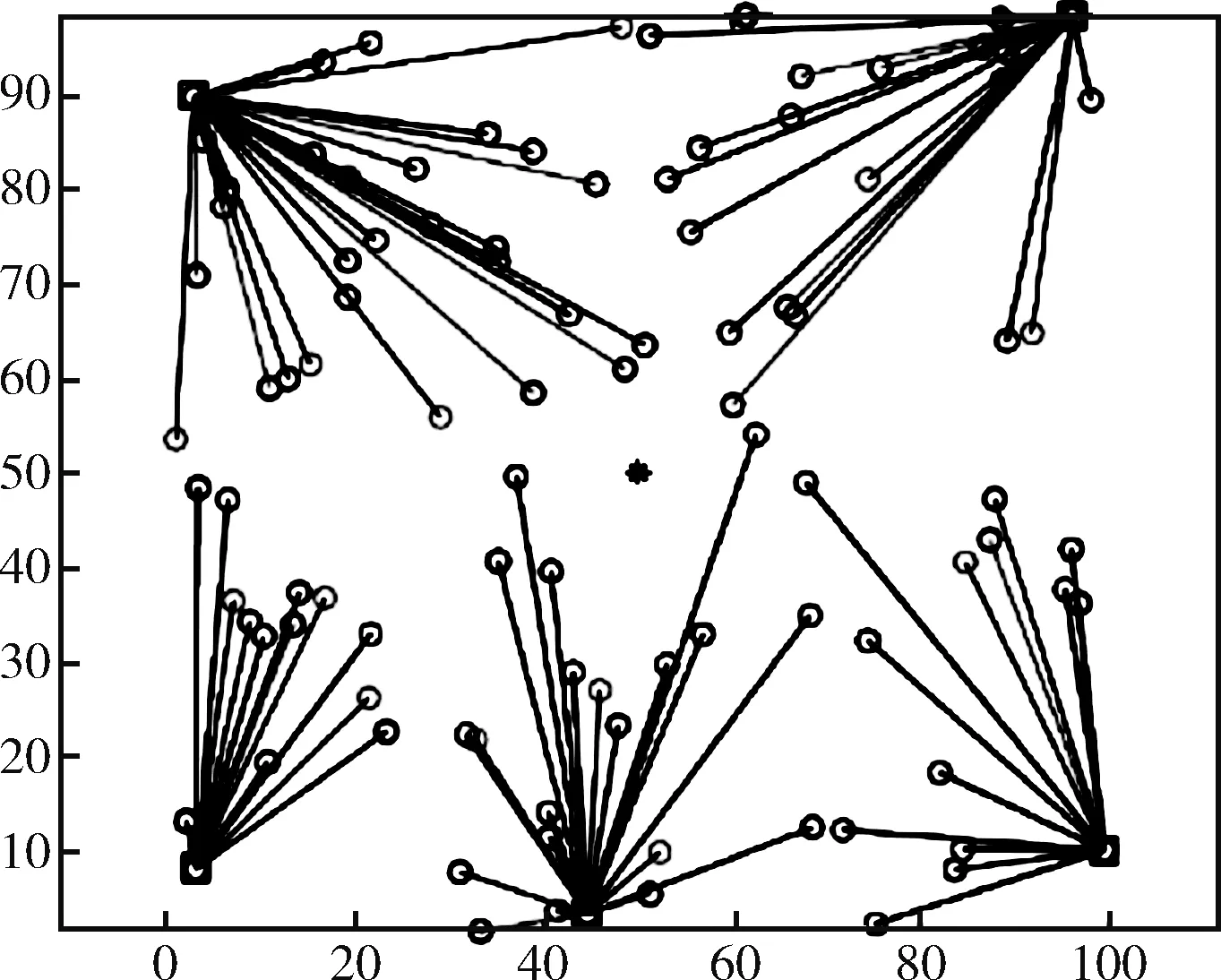
图1 网络初始成簇
根据图1可以看出,其中心聚类节点的位置在网络各方向均有分布,每个聚类中心的簇内成员数大小差异不大,以此初始中心节点方向进行中心聚类节点位置更新,不容易造成中心聚类节点距离过近,从而形成局部最优的问题。
3.1.2 聚类结果仿真分析
为更好对比聚簇的实验效果,LEACH路由协议放入4组在不同轮次中的成簇效果,将其与DMBC协议的聚类结果进行对比。实验结果如图2所示。
图2为随机选取轮次的LEACH协议成簇效果,图3为改进过聚类方法的K-means算法最终成簇效果。根据图2(a)、图2(b)、图2(c)、图2(d)显示,LEACH协议的簇首节点分布随机性强但簇群大小差异大,簇头节点分布位置也不均,从而导致部分节点死亡过快,造成能耗不均的问题。而改进的K-means算法形成的各簇群节点个数差异较小,且簇群位置根据初始成簇方向迭代形成,簇群分布均匀。从图中的成簇效果也可以看出,中心点位置并没有因为簇群中的边界节点而偏移至边界点方向,在数据传输过程中能够更好均衡网络能耗。
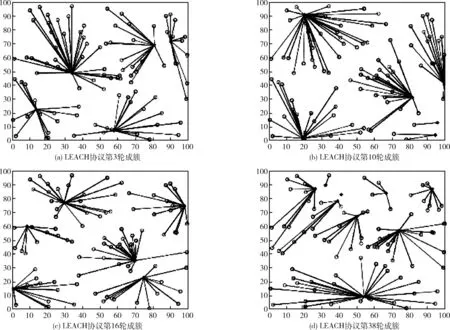
图2 LEACH协议成簇实验结果

图3 优化K-means算法成簇效果
3.2 网络生命周期仿真分析
随着网络运行时间的增加,区域中的存活节点数反映出网络生命周期的长短,而生命周期也是表示算法是否改进的重要指标。通过不同算法的存活节点数能够更加直观对比生命周期的变化,实验结果均取自多次实验的平均值,结果如下:
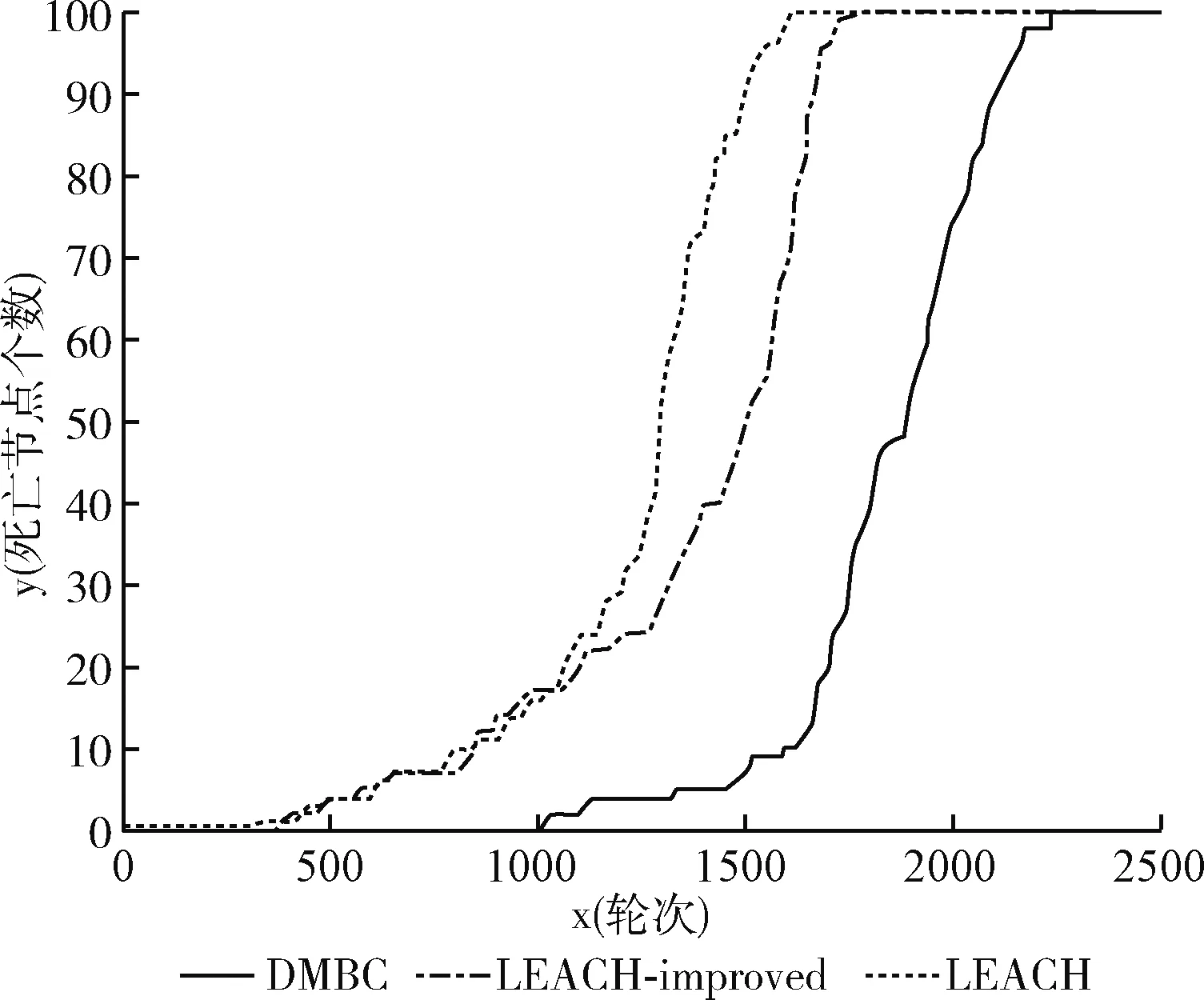
图4 死亡节点与轮次关系(Sink位于中心)
图4与图5比较了Sink节点不同方位时,各路由算法死亡节点随轮次变化的差异性。其中,图4是在Sink节点坐标为(50,50)场景下,死亡节点随运行时间变化关系。根据多次实验统计的平均值,得出以下结论:DMBC路由协议第一个死亡节点出现时间相较于LEACH-improved协议延长了百轮以上,并且DMBC路由算法在网络运行至1500轮之后仅仅只有10个以内的节点死亡,说明优化的K-means聚类算法能够有效的均衡网络能耗缩短簇头节点死亡的时间,而整个网络所有节点死亡时间相较于其它两算法也有效的往后延长至2000轮之后。
由于在多数场景中,Sink节点可能远离于传感器节点部署区域。因此,图5是汇聚节点坐标为(100,100)时,各算法死亡节点数的情况。由图可知,LEACH协议的生命周期最短,而LEACH-improved算法效果会比Sink节点位于中心时效果更优,但是即使不改变DMBC阈值中调节系数的情况下,其死亡节点数仍然相较LEACH-improved协议更少。
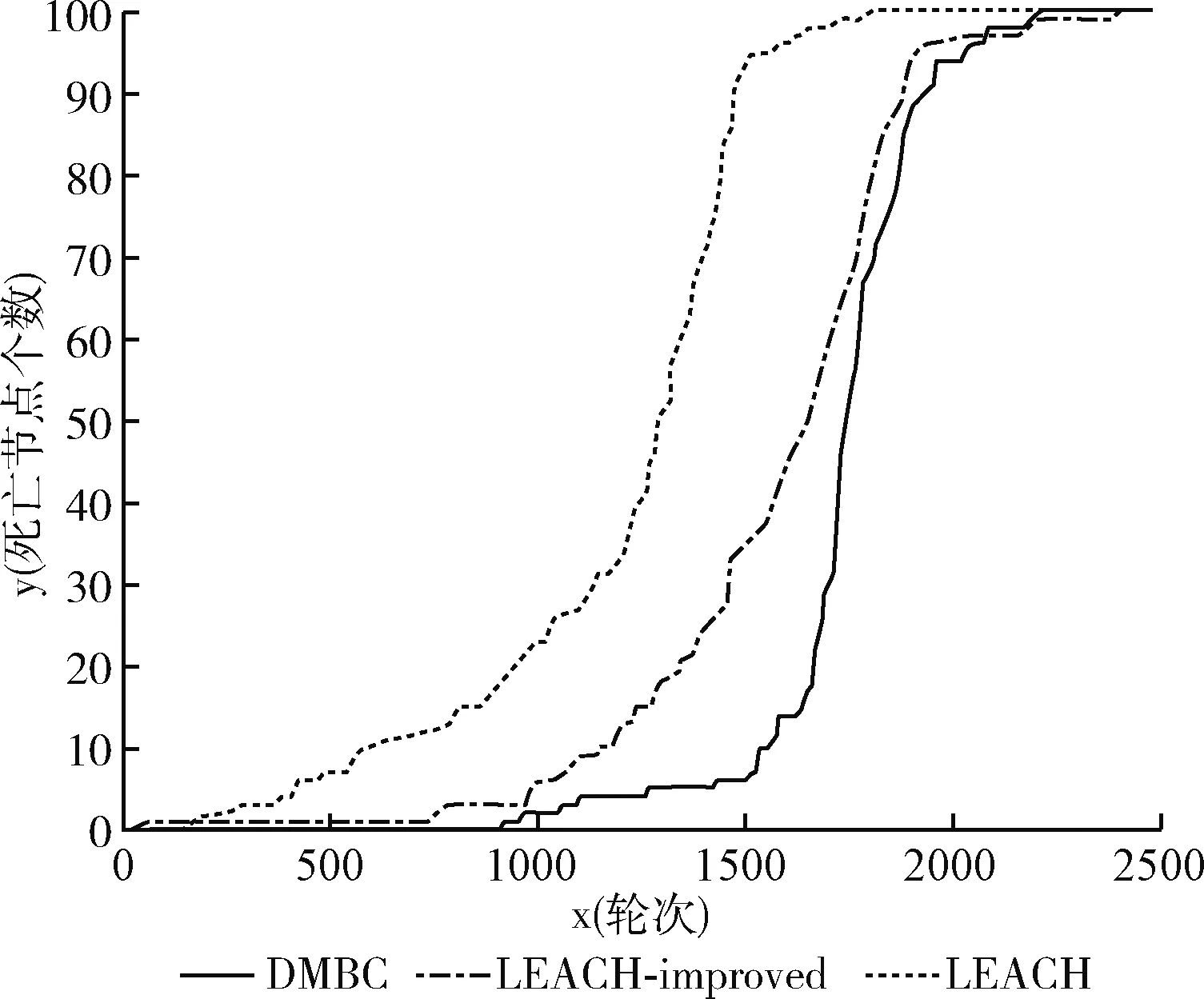
图5 死亡节点与轮次关系(Sink位于边界)
3.3 剩余能量仿真分析
网络中衡量节点利用率的重要指标是节点剩余能量,图6为区域100×100,100个节点,Sink节点位于中心,假定节点的初始总能量为0.5 J,初始总能量为50 J的仿真结果。在相同轮次时,如图所示,当轮次运行至1000轮时,LEACH协议总体能量所剩不足10 J,而LEACH-improved协议所剩能量还有10 J~15 J,而DMBC路由协议剩余能量还有初始总能量的一半以上。由此可知,本文路由协议均衡网络能耗的效果最佳,生命周期延长效果最好。
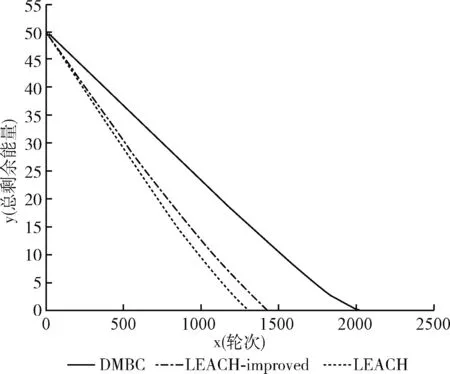
图6 总剩余能量与轮次关系
4 结束语
本文提出了节点间距离度量法聚类的无线传感器网络路由算法——DMBC。结合最优簇头数,最大距离以及节点间距离度量法的优化的K-means算法,该算法将网络节点划分为K个非均匀的簇群进行网络分区,簇群均匀分布在区域各方向,能够改善在数据传输阶段能耗不均的问题;改进聚类方式的同时也改进了簇头选举机制。通过实验仿真对比,相比于LEACH协议和LEACH-improved协议,本文协议改善了簇头分布不均问题,也解决了网络运行时簇头个数太多或太少的问题;在网络传输过程中,LEACH协议及LEACH-improved协议中簇群过大或者是过小的问题均得到改进。因此,在能耗均衡和网络生命周期仿真结果,DMBC路由协议的效果均有较明显的提升。
