多源覆盖信息系统下的加权广义多粒度粗糙集模型及其应用*

骆公志，陈佳馨

(南京邮电大学管理学院，江苏 南京210003)

1 引言

信息时代的发展促使信息来源日益增多，数据形式也越来越复杂，因此有学者提出多源信息系统MsIS(Multi-source Information System)[1]的概念，以帮助决策者做出正确选择。目前多源信息系统被广泛应用于粒计算[2]、深度学习[3]和风险评估[4]等领域，同时如何在多源信息系统中获取有用的知识也成为研究热点。

经典粗糙集中的等价关系并不能有效处理存在多种属性值的信息表，而覆盖关系粗糙集弥补了这一缺陷[5]。之后，不断有学者在此基础上对覆盖粗糙集进行改进：Zhang等[6]通过建立基于覆盖关系的直觉模糊粗糙集模型，深入探讨了多属性决策问题；Wang等[7]利用矩阵研究了覆盖粗糙集中的最大描述和最小描述的相关问题；Han等[8]基于局部有限覆盖近似空间，提出了H-粗糙集算子和K-拓扑粗糙集算子。

为分析有多粒度结构的信息表，Qian等[9,10]构造了多粒度粗糙集模型，并在此基础上引入决策理论，提出了多粒度决策粗糙集的概念。考虑到决策过程中可能存在少数服从多数的情况，Xu等[11]建立了广义多粒度粗糙集并在此基础上引入双量化决策关系，对模型进行了改良；Sang等[12]将多源信息系统和广义多粒度粗糙集结合，获取了新模型的上、下近似。有学者针对实际应用中粒度重要性的差异，对多粒度粗糙集进行了扩展,Ji等[13]基于粒度加权和粗糙集理论在直觉模糊系统中进行决策研究；Guo等[14]从决策树学习的角度，创造性地提出了3种加权多粒度区间值决策理论粗糙集。

多源覆盖信息系统中的数据具有一定复杂性，本文引入诱导覆盖粗糙集，构造了多源覆盖信息系统下的广义多粒度粗糙集MCS-GMRS(Generalized Multi-granulation Rough Set of Multi-source Covering information System)模型。文献[12]认为每个信息系统重要性相同，并未考虑到实际决策过程中，由于信息来源不同，每个信息系统对决策的支持程度会有所差异，因此本文对每个信息系统的属性赋予一定权重值，并定义了权重的计算方法，以避免因依据专家经验确定权重而产生主观性误差，进而提出了多源覆盖信息系统下的加权广义多粒度粗糙集MCS-WGMRS(Weighted Generalized Multi-granulation Rough Set of Multi-source Covering information System)模型，并通过理论和实验分析对其相关性质进行了验证。

2 预备知识

2.1 诱导覆盖粗糙集

定义1[5]设U为论域，C={X|X⊆U}是U的子集族，若C≠∅，且∪C=U，则称C是论域U上的一个覆盖，(U,C)为覆盖近似空间。

定义2[5]若(U,C)为一覆盖近似空间，对∀x∈U,Cx=∩{Cj|Cj∈C,x∈Cj},则Cov(C)={Cx|x∈U}被称为由C诱导的覆盖。

定义3[5]若Δ={C1,C2,…,Cm}是论域U上的一个覆盖族,对任意目标集X⊆U，对象x∈U有Δx=∩{Cix|Cix∈Cov(Ci),x∈Cix},那么Cov(Δ)={Δx|x∈U}被称为由Δ诱导的覆盖。

定义4[5]若IS=(U,AT∪DT,V,f)为一覆盖信息系统，A⊆AT为属性子集，CA(x)为对象x∈U在属性A下产生的覆盖类，则目标集X关于A的下、上近似分别如式(1)和式(2)所示：

(1)

(2)

2.2 多源信息系统下的广义多粒度粗糙集

定义5[15]设ISi=(U,AT∪DT,Vi,fi),对∀i∈N*,则称MS=(IS1,IS2,…,ISm)为一多源信息系统,ISi为一多源信息系统的第i个信息系统。

定义6[12]设MS=(IS1,IS2,…,ISm)为一多源信息系统，ISi=(U,AT∪DT,Vi,fi),A⊆AT为属性子集，D/DT={D1,D2,…,Dn}为决策类，φ∈(0.5,1],对∀X⊆U,定义多源信息系统下的广义多粒度粗糙集(MS-GMRS)的下、上近似分别如式(3)和式(4)所示：

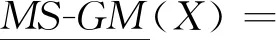
(3)

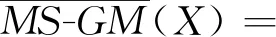
(4)

其中，x∈U在信息系统ISi下关于集合X和补集XC的支持特征函数分别如式(5)和式(6)所示：

(5)

(6)

3 多源覆盖信息系统下的加权广义多粒度粗糙集

3.1 多源覆盖信息系统下的广义多粒度粗糙集

定义7设MCS=(IS1,IS2,…,ISm)为一多源覆盖信息系统，ISi=(U,AT∪DT,Vi,fi),A⊆AT为属性子集，CISi(x)为诱导覆盖类，D/DT={D1,D2,…,Dn}为决策类，φ∈(0.5,1],对∀X⊆U,多源覆盖信息系统下的广义多粒度粗糙集(MCS-GMRS)的下、上近似分别如式(7)和式(8)所示：

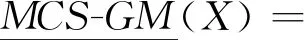
(7)

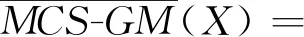
(8)

其中，x∈U在信息系统ISi下关于集合X的支持特征函数如式(9)和式(10)所示：

(9)

(10)

定义8设MCS=(IS1,IS2,…,ISm)为一多源覆盖信息系统，ISi=(U,AT∪DT,Vi,fi),A⊆AT为属性子集，CISi(x)为诱导覆盖类，D/DT={D1,D2,…,Dn}为决策类，φ∈(0.5,1],对∀X⊆U,多源覆盖信息系统下的广义乐观多粒度粗糙集MCS-OMRS(generalized Optimistic Multi-granulation Rough Set of Multi-source Covering information System)和多源覆盖信息系统下的广义悲观多粒度粗糙集MCS-PMRS(generalized Pessimistic Multi-granulation Rough Set of Multi-source Covering information System)的下、上近似分别如式(11)～式(14)所示：

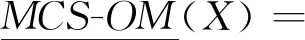
(11)

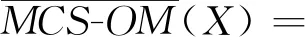
(12)

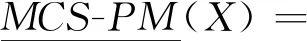
(13)

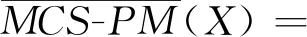
(14)

3.2 多源覆盖信息系统下的加权广义多粒度粗糙集MCS-WGMRS

(15)

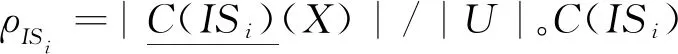
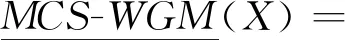
(16)

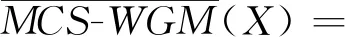
(17)

其中，x∈U在信息系统ISi下关于集合X的支持特征函数如式(18)和式(19)所示：

(18)

(19)

规则1在MCS-WGMRS模型中，对∀X⊆U，决策规则如下所示：

(P)If∑{ωi|CISi(x)⊆X}≥φ,decidex∈POS(X);

(B)If∑{ωi|CISi(x)∩X≠∅}>1-φand ∑{ωi|CISi(x)⊆X}<φ,decidex∈BND(X);

(N)If∑{ωi|CISi(x)∩X≠∅}≤1-φ,

decidex∈NEG(X)。

由规则1可知，如果满足CISi(x)⊆X的信息系统的属性权重和大于或等于φ，则决定x∈POS(X);如果满足CISi(x)∩X≠∅的信息系统的属性权重和大于1-φ且满足CISi(x)⊆X的信息系统的属性权重和小于φ,则决定x∈BND(X);如果满足CISi(x)∩X≠∅的信息系统的属性权重和小于或等于1-φ，则决定x∈NEG(X)。

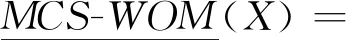
(20)

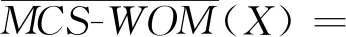
(21)

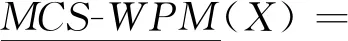
(22)

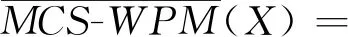
(23)

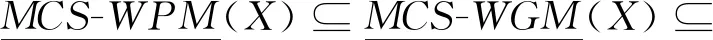
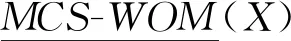
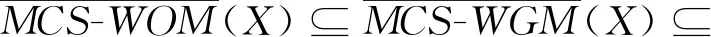
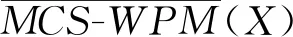
由定义10和定义11可证。

(1)当ω1=ω2=…=ωm=1/m时，有：

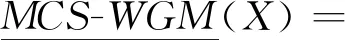
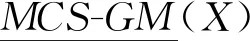
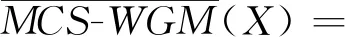
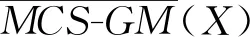
(2)当阈值φ1≤φ2时,则有：

□

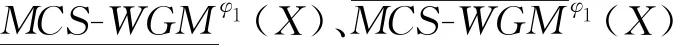
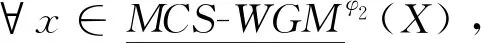
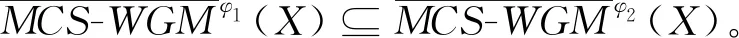
由上述定理可知，φ的取值会影响上、下近似计算结果，在实际应用中决策者根据相关情境调整阈值可以得到不同的决策结果。

(24)

(25)

(26)

目标集X的分类质量定义如式(27)～式(29)所示：

(27)

(28)

(29)

αWPM≤αWGM≤αWOM,γWPM≤γWGM≤γWOM

由定义10、定义11和定理1可证。

4 实例分析

企业环境成本对经济效益的重要性日益凸显，其环保投资效率成为客户决定是否与其开展合作的关键因素，因此客户会在投资或合作前对环保投资效率进行评估。由于评估者将环保投资效率分为多个等级，所以可能会出现多个评估结果，进而产生覆盖信息。

表1所示为一个关于企业环保投资效率评估的多源覆盖信息决策系统实例。其中MCS=(IS1,IS2,IS3,IS4)表示4个评估机构；U={x1,x2,x3,x4,x5,x6,x7,x8}为对象集，表示待评估的8个企业；属性集AT={a1,a2,a3},分别表示评估指标“经济效率”“环境效率”和“社会效率”，其取值为{1,2},表示效率等级为“低”“高”。令A={A1,A2,A3}={{a1},{a2},{a3}}，D/DT={D1,D2}={x1,x2,x4,x5,x6,x8}为决策类集合，xi,i=1,2,…,8的取值为{0,1},分别代表客户选择“不合作”“合作”，并取D1为目标集X,阈值φ=0.6。

(1)计算在信息系统IS1、IS2、IS3和IS4下每个对象的诱导覆盖类，计算结果如表2所示。

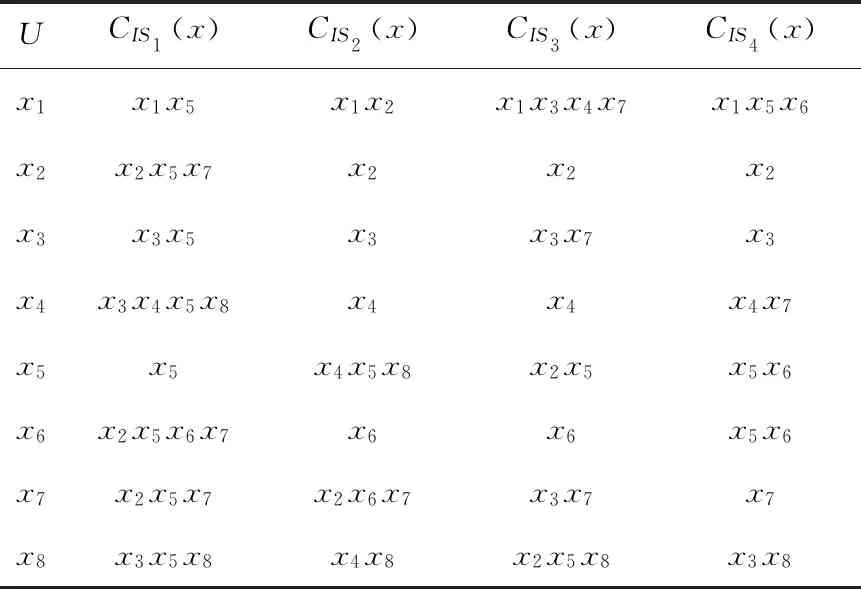
Table 2 Induced coverage relationship表2 诱导覆盖类

(2)根据定义计算每个信息系统的属性权重：

(3)当φ=0.6时，根据定义计算目标集X在相关模型的上、下近似：

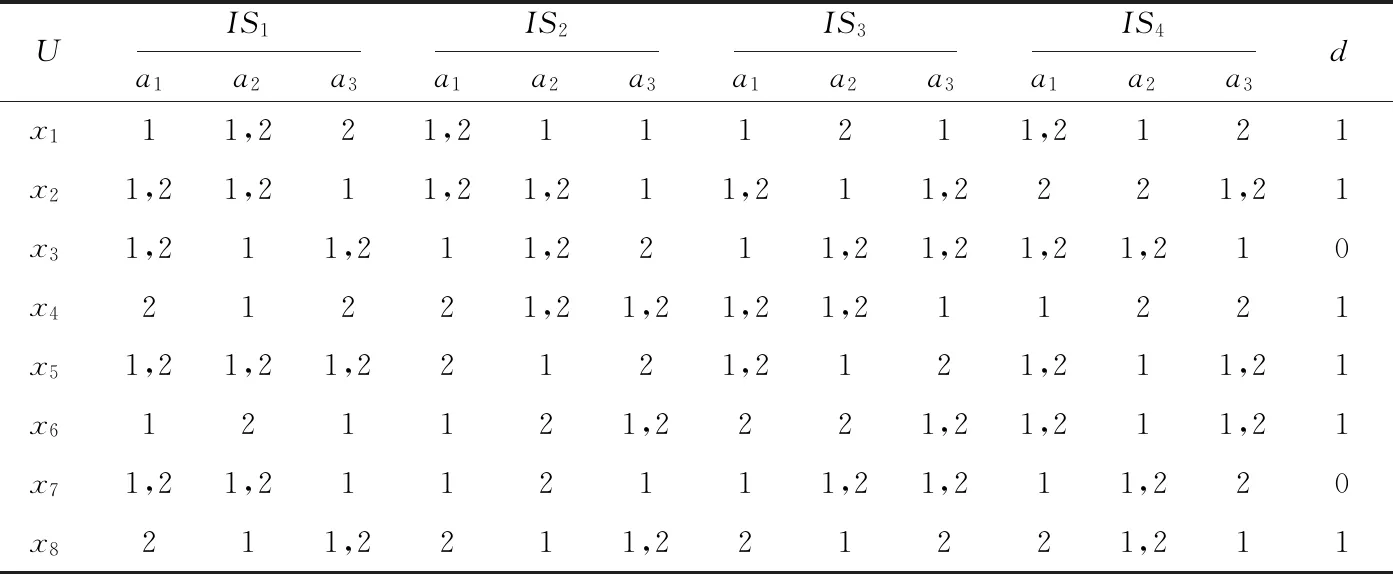
Table 1 Multi-source coverage information decision system for enterprise environmental protection investment efficiency evaluation表1 企业环保投资效率评估多源覆盖信息决策系统

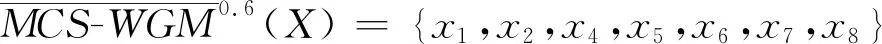
(4)计算目标集X的近似精度和分类质量：

由计算结果可得：

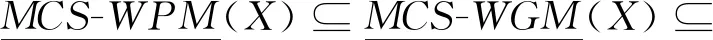
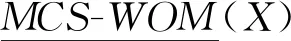
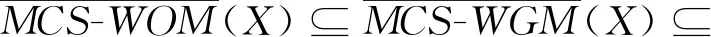
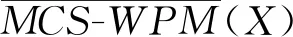
αWPM≤αWGM≤αWOM,γWPM≤γWGM≤γWOM

因此可验证定理1和定理2。

(5)通过实例进一步讨论φ的取值对上、下近似及分类质量的影响。

当φ=0.7时：

当φ=0.8时：

(6)计算结果表明，随着φ值的减小，MCS-WGMRS模型的下近似集变大，对目标集的分类也越精确。因此，根据多源覆盖信息系统合理调整φ值的大小，可以降低噪声数据的影响，使模型具有较强的容错能力，并能提高MCS-WGMRS对目标集的分类精度，帮助决策者采取更加有效准确的决策方案。

(7)为进一步验证MCS-WGMRS模型的有效性，当φ=0.6 时，计算目标集X在MCS-GMRS模型的上、下近似和相关度量参数，可得：

5 结束语

本文利用诱导覆盖关系处理覆盖信息的优势，提出了多源覆盖信息系统下的广义多粒度粗糙集(MCS-GMRS)。考虑到实际应用中数据来源的不同，对每个信息系统的属性赋予权重值，并在MCS-GMRS基础上构建了多源覆盖信息系统下的加权广义多粒度粗糙集(MCS-WGMRS)，所提出的计算权重的自适应性方法可以一定程度上避免由于专家判断失误产生的影响。本文给出了模型完整的上、下近似，详细讨论了MCS-WGMRS模型的相关定理和决策规则，并结合实例分析验证了MCS-WGMRS模型的分类能力更强，具有更高容错性，是一种处理多源覆盖信息的有效途径。MCS-WGMRS是对多粒度粗糙集的进一步推广，未来应从属性约简、机器学习等角度对该模型进行深入剖析。