基于双编码分析系统的数学课堂师生行为分析——以“二次函数”教学为例

蒋明雪， 吴立宝

(天津师范大学 教育学部， 天津 300387)

1 问题的提出

教师的课堂教学行为直接影响着课堂教学的效果，课堂教学语言是课堂教学行为的主要因素，对教学效果起着至关重要的作用[1].教学语言是教师教和学生学的基本途径，是师生交流、思想传播的媒介，更是教师基本能力和专业素养的体现，弗兰德斯也曾提出课堂教学中语言占用三分之二的时间.在人工智能与大数据时代下，教师课堂的言语行为正在向智能分析、获取特征、优化建议的方向稳步前进[2].当前有关“教学评一致性”的教学理论研究日益增多，只有教、学、评相一致，课堂质量才能高效提升[3].那么对教学行为进行分析，不仅可以帮助教师认识到教学行为的不足，进而实施改进，促进学生学习，还能够通过教师对课堂的把握和引导以及教师的行为和语言，为教学评价提供参考.因此，对课堂教学行为中教师和学生的行为进行分析具有重要意义.以一节初中数学“二次函数”课堂教学视频为例，将课堂教学中师生的行为进行编码分类，利用课堂互动双编码分析模型量化处理其课堂教学中的行为，以此来分析课堂教学中师生行为的特征.

2 研究工具

2.1 工具选择

弗兰德斯互动分析系统是美国学者弗兰德斯在20世纪60年代提出，该系统可以对课堂行为进行记录和分析，获得课堂中师生互动的情感及过程[4].弗兰德斯互动分析系统能够量化课堂教学中的语言交互行为，通过编码统计并进行分析，广泛应用于课堂教学分析中.但它也存在着只关注语言行为，忽略学生练习操作、信息技术使用等其他教学行为和问题.因此顾小清等[5]对此进行了改进，增加了信息技术的分类，在此基础上提出互动分析编码系统ITIAS.武小鹏等[6]为了将整体教学观和数学教学有机融合，使其对数学课堂分析更具有专业性，提出了基于数学学科的课堂互动双编码分析模型MFIAS，研究对MFIAS进行个别的改进后用做分析工具.

2.2 工具简介

MFIAS在“教师语言”“学生语言”“沉寂混乱”10个分类基础上，将数学课堂教学语言细分为24项，将数学教师语言和学科特点相结合，体现了数学学科的内涵.在此基础上进行改进后，在“提问”下增加“回顾总结”，即对知识内容总结进行总结性提问，让学生思考总结；在“教师指令”下增加“过渡语句”，即用于推进教学过程的指令；“交流讨论”为学生之间的语言，故将“交流讨论”纳入学生语言分类下；将“无效状态”作为一级编码，有助于与编码11中具备研究意义的课堂行为进行区分.其中对“提问”和“讲授”进行了细致的划分：“提问”划分为“对错判断(编码4a)”“概念理解(编码4b)”“解题探究(编码4c)”“回顾总结(编码4d)”；“讲授”具体划分为“内容陈述(编码5a)”“方法演示(编码5b)”“理论概念(编码5c)”“解题思路(编码5d)”.具体如表1所示.

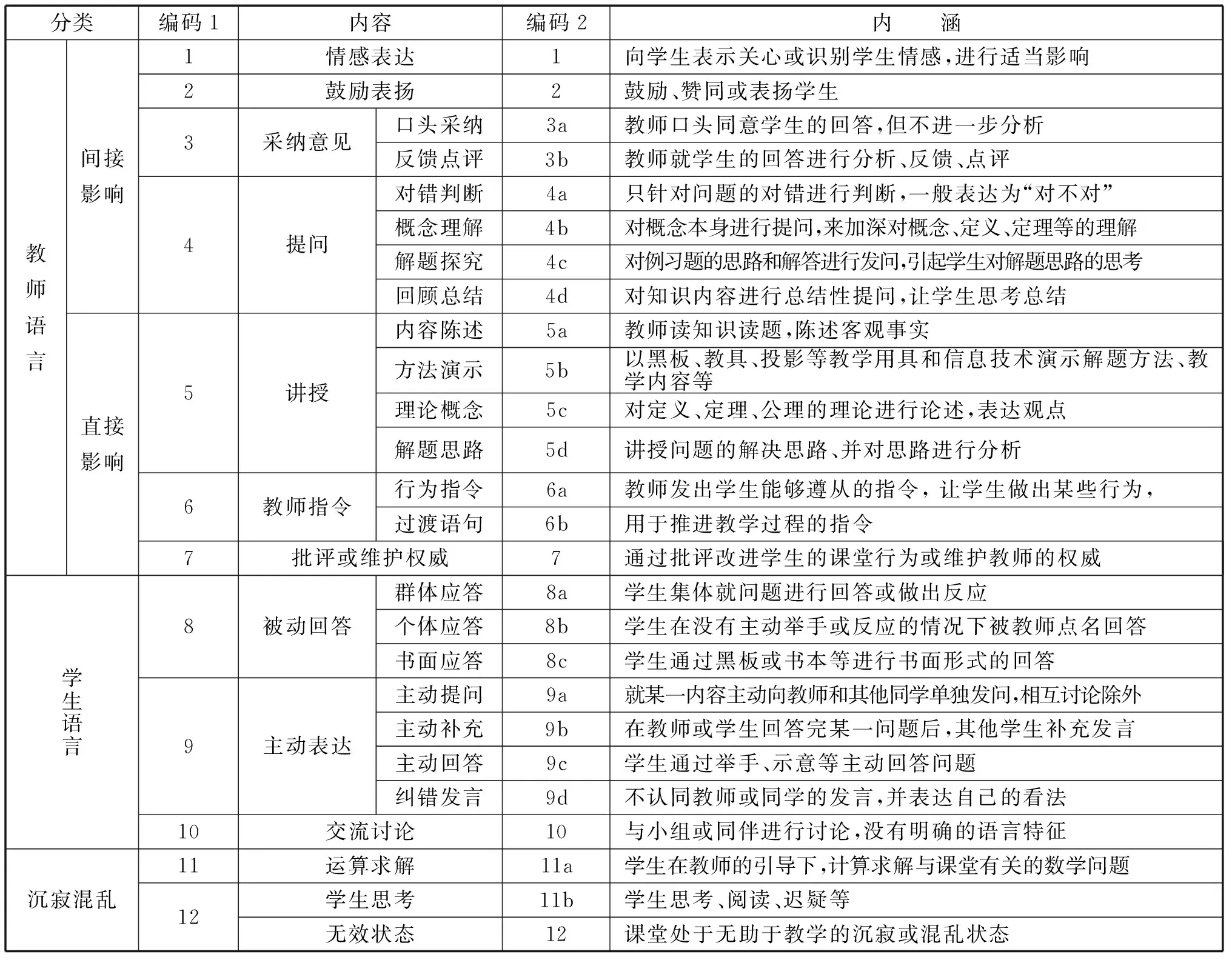
表1 数学课堂师生行为双编码分析

该分析系统与FIAS系统的课堂分析步骤是相似的，将具体言语行为进行编码，采用序对的方式将编码形成分析矩阵，对数据进行分析.即进行教学行为结构、课堂行为分布、教师语言影响、课堂行为动态等分析.

3 研究过程

视频选自“一师一优课，一课一名师”平台中的部级优课“二次函数”.本节课为新授概念课，课堂气氛活跃，师生状态良好，适合用作研究的分析视频.

在确定研究工具后，由两位编码员协同完成对本节课的编码.两位编码员反复认真观看课堂教学视频，采用时间抽样的方法，每隔3s取样记录一次，根据数学课堂师生行为双编码分析系统，把记录的编码依次按顺序排列.本节课教学时长为43′24″，共形成编码868个，组合的序对共计867个，其中两位编码员一致编码数为812个，一致性为93.55%，一致性良好，符合编码要求.基于对师生行为的编码就会产生有顺序的编码项，前后编码组成序对，统计各序对的频数，形成分析迁移矩阵.

下面将从四方面对分析迁移矩阵中的数据进行统计与分析，包括教学行为结构，即对教师语言、学生语言和沉寂混乱比例进行分析；课堂行为分布，即依次研究分析课堂总体行为、教师行为、学生行为；教师语言影响，即对教师的间接语言和直接语言、积极影响和消极影响进行分析；课堂行为动态，即课堂中每分钟师生行为的各自占比情况，了解师生行为的动态，总结师生行为特点.

3.1 教学行为结构分析

通过上述的编码过程，统计编码2中的各项频数并用得到的各项频数除以总频数868，得到各项编码的百分比，如表2所示.

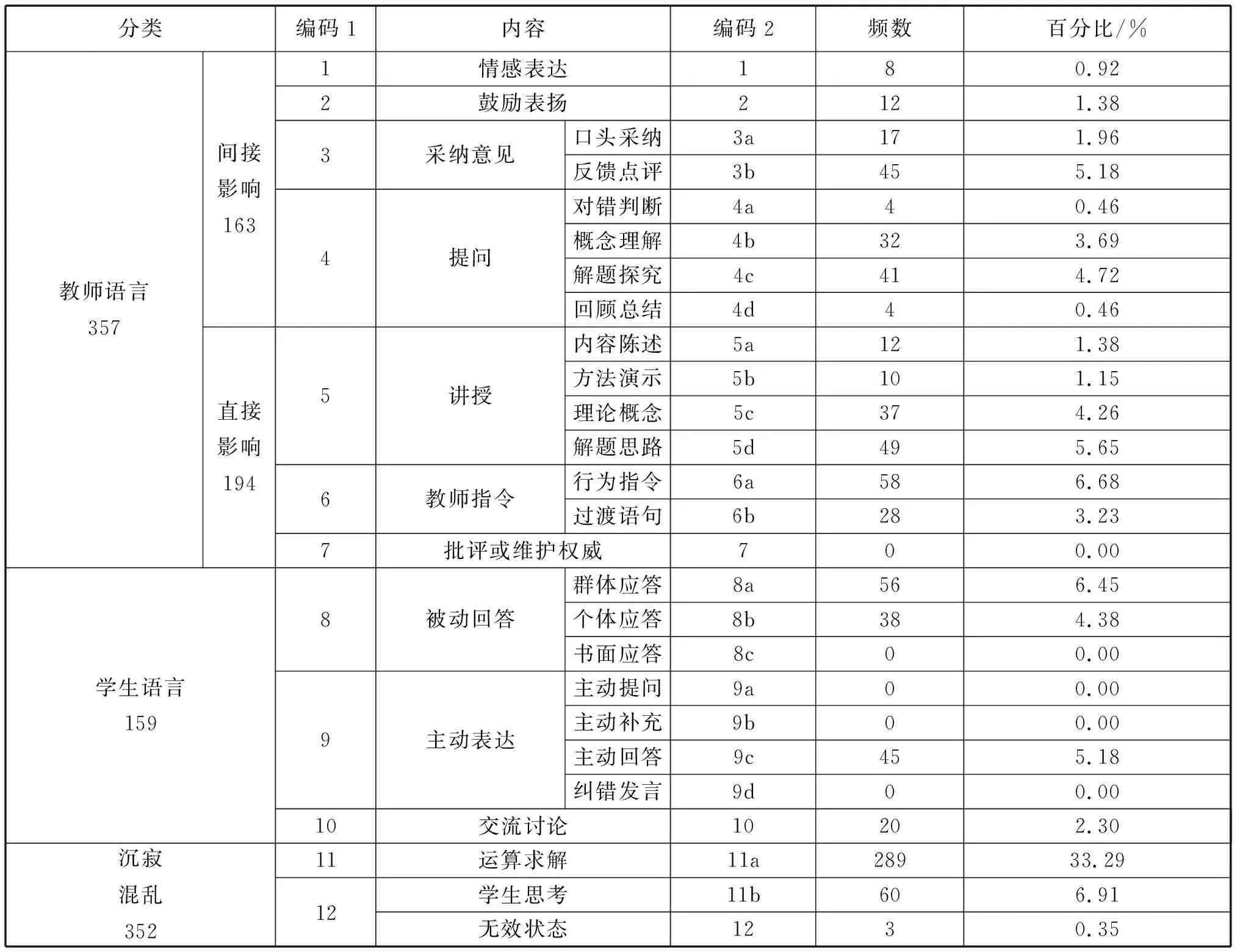
表2 编码统计表

在双编码互动模型中，课堂行为分为教师语言、学生语言和沉寂混乱3大类，可以发现：教师语言占比为41.12%，其中教师的提问和讲授行为占教师语言总时间的较大比例，学生语言占比为18.31%，沉寂混乱占比40.55%.在师生语言方面，虽然教师语言百分比大于学生语言百分比，但沉寂混乱中，几乎都是学生进行有效的思考求解，除去无效状态，该课例中学生行为共占比58.52%，说明该教师“二次函数”新授课中将课堂更多时间交给学生，通过适当的引导将课堂还给学生.在教师语言占比中，教师的行为指令占比9.91%，大部分多为有助于教学的指令，推进课堂的进展；批评或维护权威占比为0%，说明学生课堂表现良好，教师将语言更多的转为鼓励表扬.在学生语言占比中，学生主动回答占比5.18%，比被动个体应答较高，说明学生主动性较强；学生沉寂混乱占比40.55%，比例很高，其中大部分时间为运算求解和学生思考，这说明教师给了学生更多自己动手解决问题的机会，在传递知识的同时也给学生留有很多的思考时间.

3.2 课堂行为分布分析

3.2.1 课堂行为总体分布

根据数学课堂师生行为编码以及各编码的频数，绘制如图1所示的课堂教学行为频数-百分比复合图.

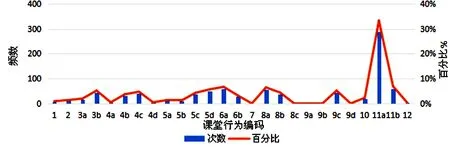
图1 课堂行为频数-百分比复合图

由图1可得“二次函数”课堂教学中，各个课堂行为频数的大小比较依次是“11a”>“11b”>“6a”>“8a”>“5d”>“3b”=“9c”>“4c”>“8b” > “5c”>“4b”>“6b”>“10”>“3a”>“2”=“5a”>“5b”>“1”>“4a”=“4d”>“12”>“7”=“8c”=“9a”=“9b” =“9d”.其中运算求解(编码11a)、学生思考(编码11b)、行为指令(编码6a)居前三，说明教师在课堂中能够给学生更多的时间用来思考和求解，注重课堂留白艺术.但同时由图1可以明显看出，学生除了主动回答外，编码9a，9b，9d频数都为0，并且学生语言中大多为学生的被动回答，缺乏主动提问、主动补充等行为的主动性，这不利于充分表达自己的观点，教师引导学生主动性方面也有待加强.

3.2.2 教师行为分布

教师行为包含了情感表达、鼓励表扬、口头采纳、反馈点评、对错判断、概念理解、解题探究、回顾总结、内容陈述、方法演示、理论概念、解题思路、行为指令、过渡语句、批评或维护权威共15种课堂行为.根据课堂教师行为编码以及各编码的频数，绘制如图2所示的教师课堂行为柱状图.

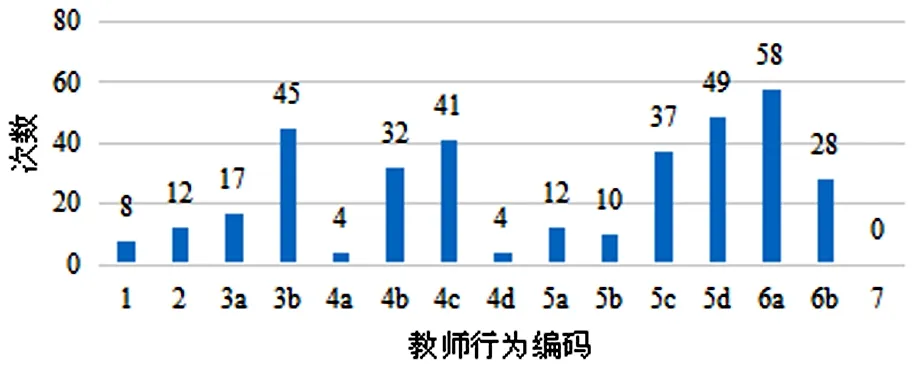
图2 教师课堂行为柱状图

由图2可以发现，在教师的语言行为中，教师讲授和指令次数最多，从迁移矩阵的各序列对数据来可以看出，“6a-8b”(行为指令-个体应答)“6a-9c”(行为指令-主动回答)“5c-5c”(理论概念-理论概念)“5d-5d”(解题思路-解题思路)的教学行为组合多次使用，故该教师以讲授和行为指令为主.教师提问的次数达到81次，由此可见该教师提问语言较多，通过提出问题来促进学生的思考，引导学生的思维.该教师采纳意见中的反馈点评(编码3b)次数达45次，说明该教师善于接受和肯定学生的回答，并就此做一定的补充，帮助学生进一步理解知识.并且从迁移矩阵的各序列对数据来看，该教师多次使用“8b-3b”(个体应答-反馈点评)和“9c-3b”(主动回答-反馈点评)的教学行为组合，这也同样说明教师能够在课堂中及时对学生的回答予以反馈，对存在的问题及时地进行指导讲解，切实实现对话导学[7].

3.2.3 学生行为分布

学生行为包含群体应答、个体应答、书面应答、主动提问、主动补充、主动回答、纠错发言、交流讨论、运算求解、学生思考、无效状态共11种课堂行为类型.根据课堂学生行为编码以及各编码的频数，绘制如图3所示的学生课堂行为柱状图.

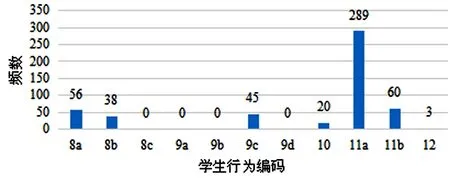
图3 学生课堂行为柱状图

由图3中的统计结果可以发现，在学生的应答方面全体应答(编码8a)次数较多，说明教师在授课过程中多运用小设问来引导全班齐声应答，调动全班学生参与到教学活动中来，但同时也说明教师提出的问题缺乏一定的深度.学生没有书面演示回答的行为，并且主动提问、主动补充、纠错发言的行为没有出现，说明该课堂中学生对学习二次函数的提问主动性不够强烈，学生多为接受学习.学生主动表达占比为5.18%，远低于被动回答占比10.83%，这说明学生的主体性不够，教师并没有将学生的被动学习转化为主动学习.在沉寂混乱中，由迁移矩阵的各序列对数据可以看出，“11a-11a”(运算求解-运算求解)“11b-11b”(学生思考-学生思考)学习行为组合分别出现267次和29次，课堂以有益的思考和求解为主，教师留给学生充分的时间去思考和求解，使学生的自主学习能力得到提升.

3.3 师语言影响分析

FIAS把教师的语言分为直接语言和间接语言两类，其中直接和间接表示的是教师对教学的控制.间接教学在鼓励和引导的情境下能够激发学习动机，相比较于直接教学而言可以促进学生更多的发言和参与，缓解学生紧张的状态，提高学业成绩.编码1-4所代表的教师语言主要是对学生态度和情绪的影响，其控制方式是间接的；编码5-7则是对学生更直接的控制.编码1、2、3表示教师的接受、鼓励和赞同，是对学生的积极影响，编码6、7是教师指令和批评维权，强制学生接受、服从，属于对学生的消极影响.根据间接影响、直接影响以及积极和消极影响的行为编码以及各编码的频数，绘制如图4所示的教师语言效果分布图.其中，属于间接影响的教师语言出现频数为163，直接影响的教师语言频数为194，积极影响和消极影响的语言频数分别为82和58.

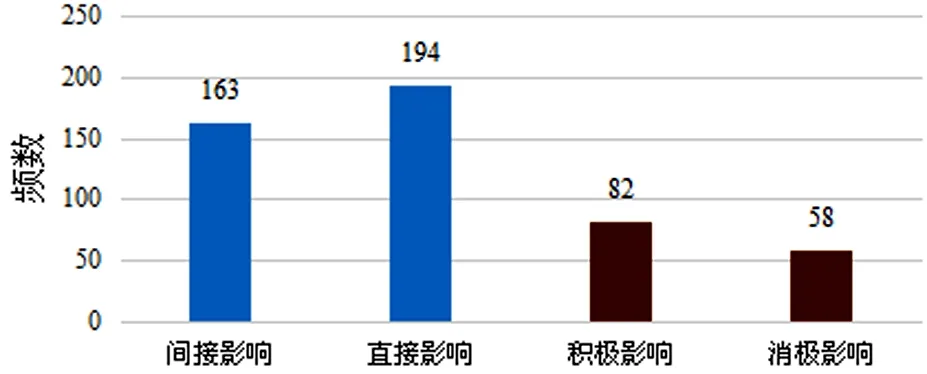
图4 教师语言效果分布

用间接影响频数除以直接影响频数可得该教师间接影响语言与直接影响语言比率为84.02%，用积极影响频数除以消极影响频数可得积极影响语言与消极影响语言比率为141.38%，由此能够说明教师在课堂中多为直接地进行掌握和调控，但同时也善于用间接语言来进行引导和激励，更多地进行积极的强化学习.再由教师行为编码图中可以看出，教师语言中批评维权(编码7)行为频数为0，教学大多是由讲授(编码5)和指令(编码6)的方式进行，其中讲授大多是对理论概念以及解题思路等行为，教师指令多为行为指令，这些行为都充分体现课堂中教师对学生的引导作用.

3.4 课堂行为动态分析

通过编码记录课堂中每分钟师生行为的各自占比情况，绘制如图5所示的课堂行为动态曲线，了解师生行为的动态，总结师生行为特点.由图5分析可得，教师在二次函数的新授课中，在第15min、33min、34min和第40min中，学生行为占比100%，因为此时教师给学生一定的时间去思考和运算求解.除此之外，在课堂的每一分钟中，教师行为和学生行为都会交替存在，由此可以说明教师注重学生的参与，体现了学生在课堂中的主体性.从图5的动态曲线还能够分析出在本节课的教学中，教师行为有12次达到某个峰值，分别是第3，6，8，12，17，19，23，26，30，36，38，43min；学生行为有11次达到某个峰值，分别是第2，4，7，9，15，21，24，28，33，37，40min.由以上各个行为峰值的出现时间能得出教师行为峰值和学生行为峰值大多是交错出现的，并且学生行为峰值在教师行为峰值之后.如教师行为达到峰值是在第3min，那么第4min就是学生行为达到峰值.由此可以说明该教师关注学生在课堂中的行为表现，教师和学生行为交替进行，师生互动良好.通过图5还可以看出在第2，3，4，5，7，8，9，10，11，13，14，15，16，24，27，28，29，31，32，33，34，35，39，40，41，42min，教师行为占比小于学生行为占比，共计出现26次，所占时间高达课堂教学总时间的59%，这又一次体现了学生为主体，教师为主导的课堂教学模式.

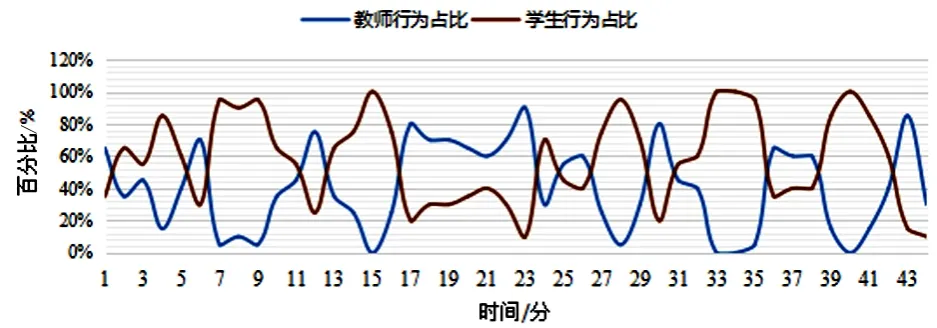
图5 课堂行为动态曲线

4 总结与建议

4.1 有效使用多种教学行为组合

教师善于采取讲授式教学，多为教师提问和讲授后学生回答问题，虽然教师的直接讲授能够让学生接受知识更加轻松，但是这就会使学生产生依赖和期待心理，难以积极主动地进行思考.所以，教师要鼓励学生主动表达自己的观点和看法，诱发学生思考，进而让学生能够用自己的语言来归纳表述[8]，即尽量提高编码9a，9b，9d的频率，以及增加教学行为“4-9”(提问-主动表达)与“5-9”(讲授-主动表达)的出现次数，提高学生的主动参与性，完成教师行为与学生行为的有效交互.不仅如此，还要灵活有效地使用多种教学行为组合，比如“8-1”(被动回答-情感表达)、“8-2”(被动回答-鼓励表扬)、“9-1” (主动表达-情感表达)、“9-2”(主动表达-鼓励表扬)，即学生在回答问题或表达观点之后，教师给予接受和表扬，让学生对数学学习有信心.教师有效使用各类教学行为组合，能够促进数学课堂教学的高效实施.

4.2 及时采纳反馈学生应答内容

在本节课中采纳意见出现62次，在教师语言中占比17.3%，多次出现“8-3”(被动回答-采纳意见)、“9-3”(主动表达-采纳意见)等教学行为组合.该教师在二次函数讲授过程中，对于学生的回答和意见，教师大都采取肯定接受并做进一步分析，及时采纳和反馈学生的应答内容，让学生的问题马上得到解决，思路想法进一步加深，有助于学生对知识的感受.教学本身就是教师教和学生学的双向交流活动，学生在回答问题后得到反馈，共同交流会让师生之间建立平等、教学相长的师生关系.作为教师要认真倾听做出应答，要欣赏学生做出应答，更要厘清责任做出应答[9]，对于学生积极做出应答，关注学生的知识水平，从而引导学生进一步学习.

4.3 充分体现课堂留白教学艺术

由课堂行为频数百分比复合图可以看出，编码11a，11b出现次数很多，充分体现该教师课堂留白的教学艺术.该教师给与学生充足的时间进行思考和解决问题，合理分配沉寂的时间，使思考解题等这些有益沉寂起到训练思维的作用，让学生能够独立思考，学生学习主体的价值得以体现.在数学教学过程中，如果都是教师在讲授而不给学生思考的时间，学生就会很容易觉得内容枯燥无味，并且会导致注意力不集中.适当的课堂留白，能够让学生有时间去思考问题和解决问题，这样可以调节教学节奏，避免沉闷、无聊的课堂氛围，还可以提高学生学习的积极性和参与感[10].并在有效利用教材内容的基础上，灵活设计探究活动，引发学生思考，促进学生思维和能力的发展[11].