基于能量耗散历史的沥青混合料疲劳损伤特性研究

2021-12-23房辰泽郭乃胜尤占平谭忆秋温彦凯

东南大学学报(自然科学版) 2021年6期

房辰泽郭乃胜尤占平谭忆秋王淋,5 温彦凯,5

(1大连海事大学交通运输工程学院, 大连 116026)(2香港理工大学土木及环境工程学系, 香港 999077)(3Department of Civil and Environmental Engineering, Michigan Technological University, Houghton, MI 49931, USA) (4哈尔滨工业大学交通科学与工程学院, 哈尔滨 150090)(5Department of Civil and Environmental Engineering, Washington State University, Washington, WA 99163, USA)

通过分析能量耗散规律表征材料的损伤,已成为研究材料结构损伤行为的重要科学手段[1-3].van Dijk等[4-5]基于所有耗散能(dissipated energy, DE)均可造成沥青混合料疲劳损伤的假定,揭示了疲劳寿命与累积耗散能的幂函数关系.Tayebali等[6]采用四点弯曲疲劳试验方法,证明了材料的疲劳寿命与累积耗散能的幂函数关系受温度和试验方法的影响.为合理地表征材料损伤,Hopman等[7]在前人研究的基础上,基于单循环耗散能演化规律,提出能量比(ratio of dissipated energy, RDE)的概念,并采用RDE判定损伤演化过程中裂纹的形成阶段,但是该方法难以通过严谨的数学手段确定唯一的疲劳失效阀值,这较大程度上限制了其在工程应用中的适用范围[8].Pronk等[9]综合考虑了单循环耗散能和累计耗散能对损伤演化过程的影响,对RDE的定义进行了改进,但仍无法捕捉沥青混合料的唯一疲劳曲线.Ghuzlan等[10-11]为更深入地研究材料损伤特性,基于耗散能变化是材料结构损伤演化诱因的假设,定义了耗散能相对变化率 (ratio of dissipated energy change, RDEC),结果表明,RDEC可通过量化耗散能的变化速率表征材料损伤,疲劳寿命与RDEC的平稳值存在唯一的幂函数关系.

研究人员通过开展室内试验建立力学模型,对RDEC法表征材料损伤及预测疲劳寿命进行了系统深入的研究[12].Carpenter等[13]通过开展疲劳愈合试验,证明了RDEC法可以较为准确地预测沥青混合料在愈合工况下的疲劳特性.Omrani 等[14]通过开展温拌沥青混合料的疲劳试验,证明了RDEC法能较为准确地表征温拌沥青混合料的疲劳特性.Khavandi等[15]通过开展低损伤水平的沥青混合料疲劳试验,证明了RDEC法能够较为准确地预测低损伤水平下材料的疲劳极限.由于RDEC法可以较为准确地揭示不同工况下黏弹性材料的疲劳损伤演化机理,为疲劳寿命预测提供理论依据,已被广泛地应用于沥青混合料疲劳特性评价以及沥青路面结构设计[16-17].

Sun等[18]、范东[19]采用RDEC法较为准确地预测了橡胶沥青混合料的疲劳寿命,并通过建立数学模型对耗散能的演化规律进行了研究,结果表明,由于单循环耗散能呈非单调演化趋势,采用单循环耗散能定义的RDEC不能充分考虑沥青混合料的能量耗散历史,导致相邻循环内表征材料损伤的RDEC会存在较大离散性,相应的损伤演化曲线近似呈直线分布状态,即RDEC无法准确地区分和描述不同工况下的非线性损伤演化行为[20-21].为弥补RDEC法的不足,本文通过开展室内疲劳试验,定义新的能量参数即累计耗散能相对变化率(ratio of cumulative dissipated energy change, RCDEC)表征材料损伤,并采用RCDEC分析疲劳损伤特性.

1 材料与试验方法

1.1 材料与试件制备

选择AC-13型橡胶沥青混合料进行室内试验,集料类型为辽阳水峪春和采石场生产的石灰岩,沥青质量分数为5.5%,橡胶沥青技术性能和级配结果分别如表1和表2所示.根据规程《公路工程沥青及沥青混合料试验规程》(JTG E20—2011)成型300 mm×300 mm×70 mm的车辙板,并通过切割车辙板获得250 mm×30 mm×35 mm的梁型试件.

1.2 试验方法

四点弯曲疲劳试验的夹具结构复杂,且对试件的成型和加载设备要求较高.而三点弯曲疲劳试验的夹具简单,对相关设备要求不高,具有可重复性强、便于推广等显著优点,且可以较为有效地研究沥青混合料疲劳特性[18-21].故本文开展三点弯曲疲劳试验,对试件中央顶部的位移和力值进行测试,采用结构力学理论得到梁型试件中央底部位置的拉伸应变和应力.

选择合适应力比是开展疲劳试验的重要步骤,单位循环内损伤累积程度与应力比负相关,应力比过小的疲劳试验耗时过长,可重复性较差,且不能较好地模拟日趋严重的重载道路工况.通过开展高应力比试验建立疲劳曲线揭示损伤演化机理,是预测研究低荷载水平下材料疲劳特性的重要手段.研究表明,开展应力比为0.6～0.8的三点弯曲疲劳试验建立疲劳方程,可以较为准确地预测沥青混合料疲劳寿命[1,3].鉴于此,本文所选应力比分别为0.6、0.7、0.8,温度分别为5、15、25 ℃,如表3所示.

具体试验步骤如下[18-21]：

① 将小梁置于设定温度的恒温水槽1 h,启动疲劳试验加载室的控温系统,使加载室与水槽温度保持一致.

② 将支座准确对中固定,并保证两支点间距为200 mm,将试件取出对称放置于支座上.

③ 启动疲劳加载程序对小梁试件进行循环加载,直至试件发生断裂.当疲劳次数达到一定次数后,小梁结构不能承受设定的荷载幅值,从而发生断裂.

发生断裂时对应的循环次数记为疲劳寿命Nf,Nf的试验结果如表3所示.由表可知,Nf与应力比负相关,与试验温度正相关.

2 RDEC与RCDEC的演化规律分析

沥青混合料的黏弹滞后特性造成材料应变响应时间落后于应力响应时间,应变和应力组成的闭路曲线的面积等于耗散能.研究表明,单个循环内耗散的能量并非全部与损伤相关,只有一部分耗散能用于产生损伤,因此采用累积耗散能表征损伤并不能深刻地揭示沥青混合料的损伤演化过程.相邻加载循环内耗散能的变化才是造成材料损伤的原因,耗散能变化速率越大,表明单个循环内越多的耗散能转化为材料损伤,即损伤演化速率越快.通过定义反映耗散能变化速率快慢的物理量表征损伤演化是研究损伤行为的有效手段[11,13,20].

2.1 RDEC演化规律分析

Ghuzlan等[10-11]基于耗散能变化是沥青混合料损伤演化诱因的假定,通过如下定义量化了耗散能的变化速率,即

(1)

式中,RDEC,N为耗散能相对变化率;DE,N为第N次加载的耗散能.

沥青混合料损伤演化速率与RDEC负相关,RDEC法已被广泛地应用于评价沥青混合料疲劳特性以及沥青路面结构设计.沥青混合料的耗散能DE与N/Nf曲线如图1所示.由图可知,耗散能随着疲劳加载的进行整体呈U形演化趋势,且耗散能整体取值水平分别与应力比和温度呈现出正相关和负相关的函数关系.耗散能变化率RDEC与N/Nf曲线如图2所示,RDEC分别在第1和第3阶段快速地减小和增加,RDEC进入第2阶段后呈波动幅度较大的离散状态,表明相邻循环内表征沥青混合料损伤的RDEC存在较大离散性,RDEC无法用于准确地描述材料损伤的连续演化行为;当试验条件变化时,曲线重合程度严重,不能通过图像直观区分,表明采用RDEC难以直观地识别区分不同试验条件下的材料损伤演化行为.

(a) 不同应力比

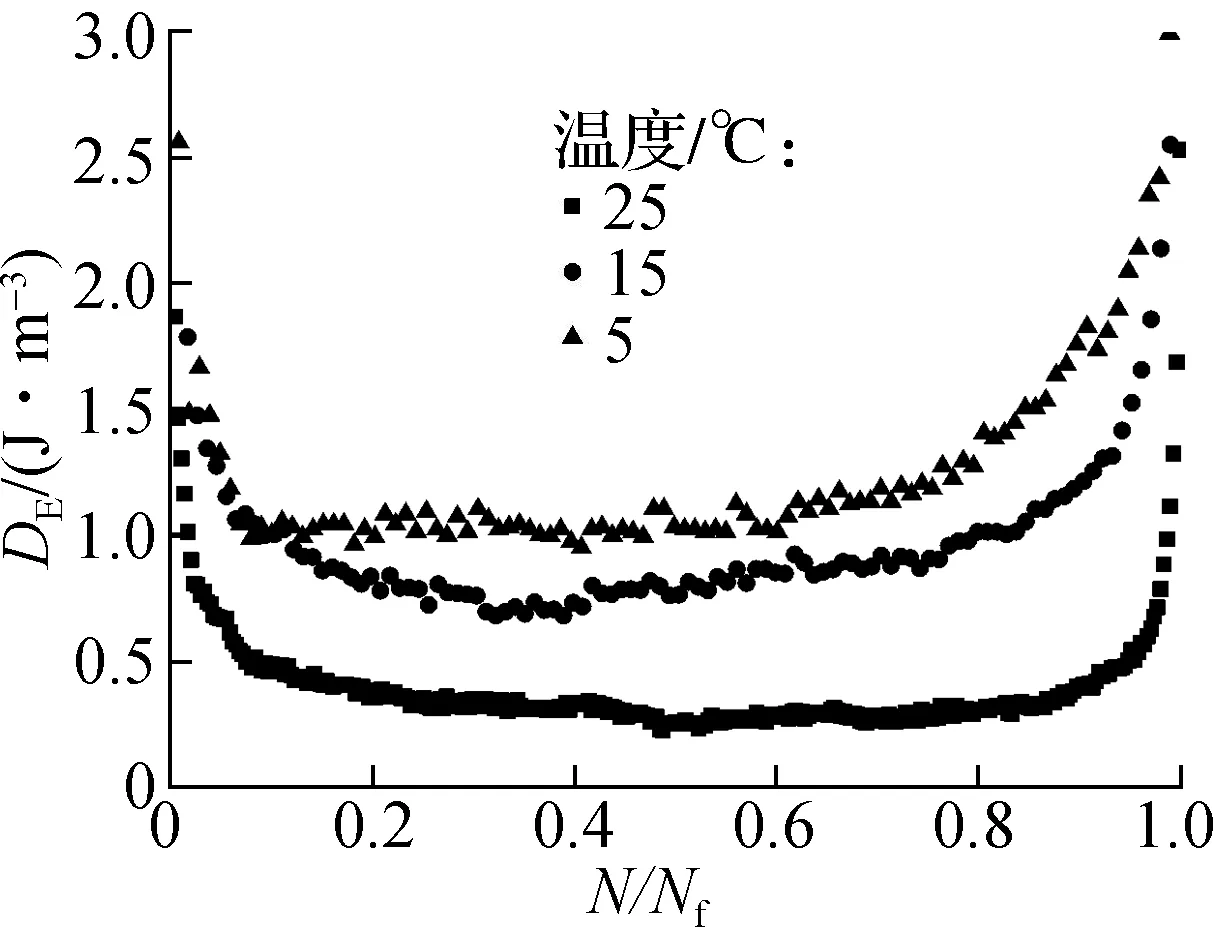
(b) 不同温度

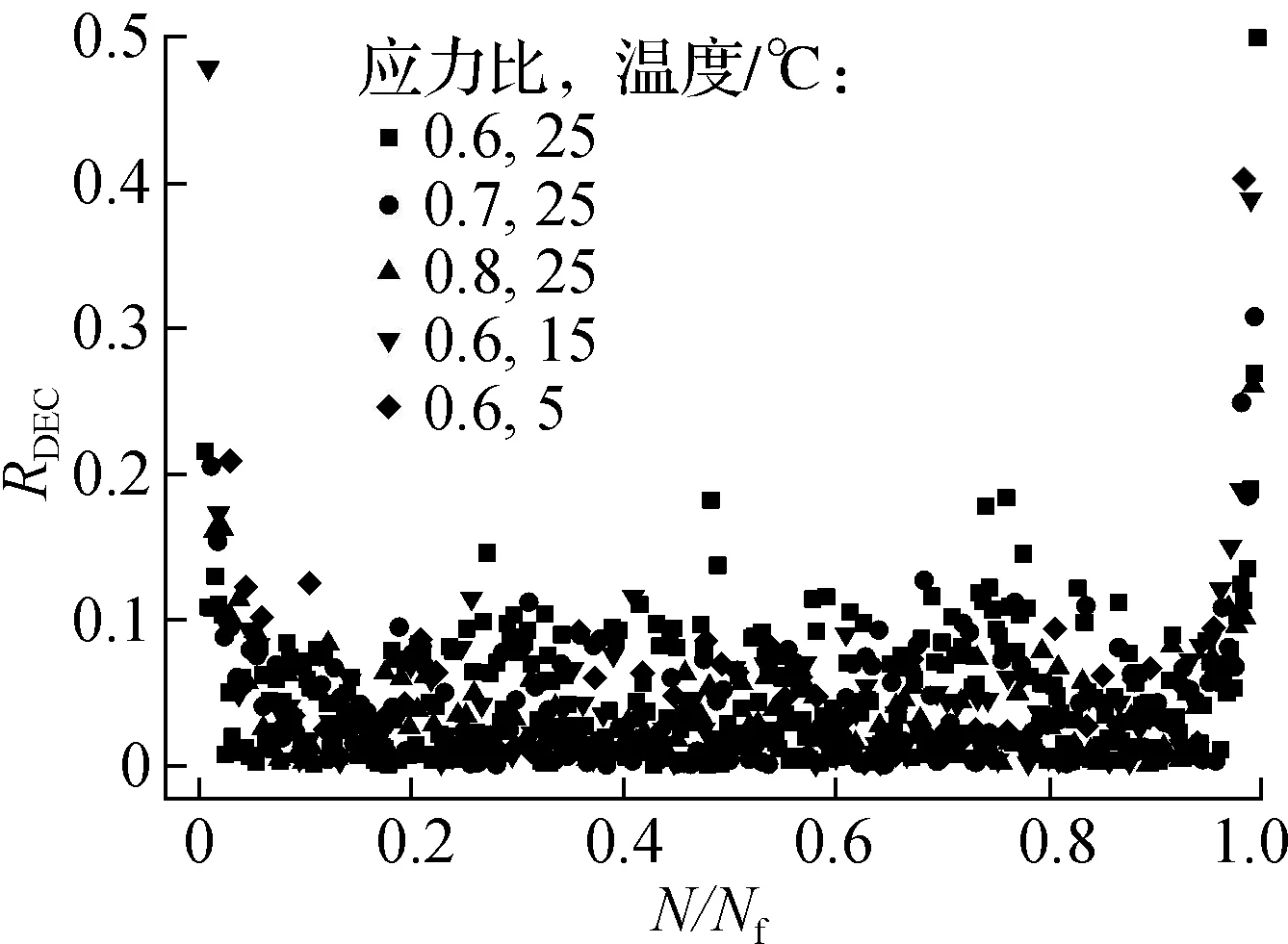
图2 RDEC-N/Nf曲线

基于RDEC演化规律定义的损伤变量计算公式如下：

(2)

式中,DR为采用RDEC定义的损伤变量;RDEC,k为第k次加载的RDEC.

DR-N/Nf曲线如图3所示,损伤虽然局部呈非线性演化,但在整个疲劳加载进程中整体呈线性演化规律,与沥青混合料典型的非线性损伤演化规律不吻合[1,22],表明RDEC参数无法准确地描述材料损伤的非线性演化行为.通过分析式(1)、(2)可知,由于单循环耗散能演化规律呈非单调趋势,且不能反映第N个循环之前的能量耗散历史,导致其定义的RDEC难以直观地识别区分不同条件下的损伤演化行为,无法准确地描述材料损伤的非线性连续演化行为.

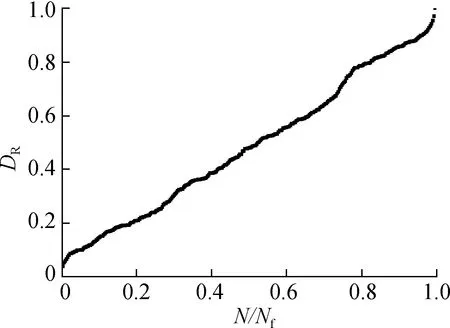
图3 DR-N/Nf曲线

2.2 RCDEC演化规律分析

累积耗散能(cumulative dissipated energy, CDE)呈单调递增趋势,且可以反映第N个循环之前的能量耗散历史,其计算公式如下：

(3)

式中,CDE,N为第N次加载的累积耗散能.

采用CDE能定义新的能量参数RCDEC,RCDEC数值愈大,表示累积耗散变化速率愈快,损伤演化速率愈快.RCDEC计算公式如下：

(4)

式中,RCDEC为累积耗散能相对变化率.

RCDEC-N/Nf曲线如图4所示.通过分析对比图2和图4可知,RCDEC和RDEC均分别在第1和第3阶段呈现出快速减小和增加的演化趋势,与RDEC第2阶段波动幅度较大的离散状态不同,RCDEC在第2阶段呈连续稳定的演化分布状态,表明RCDEC能够较为准确地表征沥青混合料的连续损伤演化状态.当试验条件变化时,RDEC-N/Nf曲线重合程度严重且难以区分,但RCDEC-N/Nf曲线几乎没有重合,表明采用RCDEC能够直观地识别区分不同试验条件下的材料损伤演化行为.基于RCDEC演化规律定义的损伤变量可按下式计算：

(5)

式中,DRC为采用RCDEC定义的损伤变量;RCDEC,k为第k次加载的累积耗散能相对变化率.

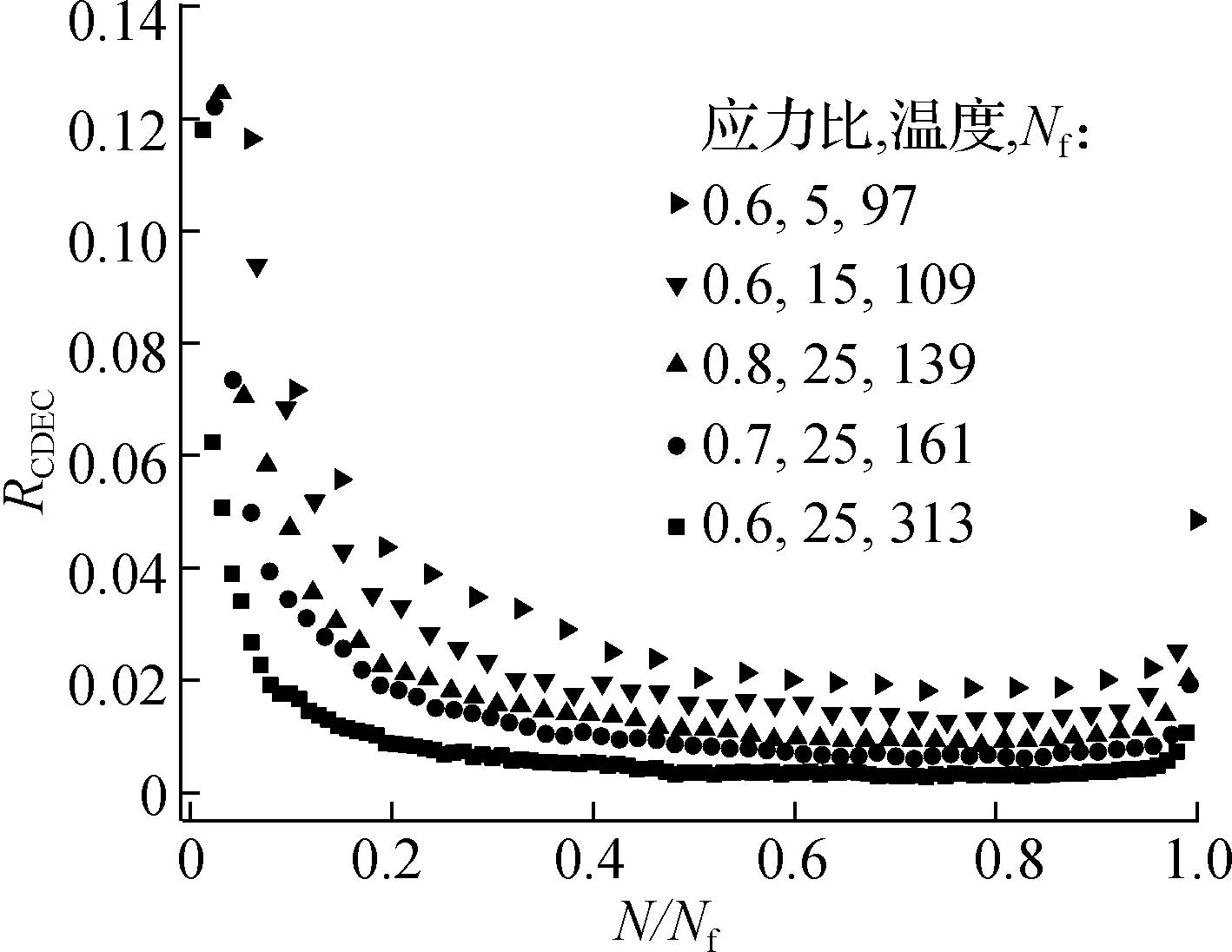
图4 RCDEC-N/Nf曲线

DRC-N/Nf曲线如图5所示.由图可知,材料损伤随着疲劳加载的进行发生非线性演化,表明采用单调递增的累积耗散能定义的RCDEC,充分考虑了沥青混合料的能量耗散历史,能够表征损伤的非线性演化行为.

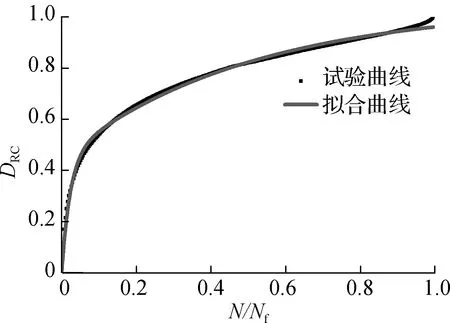
图5 DRC-N/Nf曲线

3 基于RCDEC的疲劳损伤特性

3.1 损伤模型建立

栾利强等[22]提出的ExpAssoc型损伤演化方程如下：

(6)

式中,D为损伤值;αk和βk为模型参数,与温度、应力水平相关;CR=N/Nf.该演化方程能够准确地刻画沥青混合料的非线性疲劳损伤演化规律,故本文基于该演化方程建立损伤模型.

对式(6)积分可得

(7)

式中,C为常数.

由于N=0时D=0,则得到如下损伤模型：

(8)

下面给出损伤累积的推导过程.单循环损伤增量计算公式如下：

ΔDi=DN+1-DN=

(9)

1)N=1时,初始损伤D0为0,则第1个周期对应的损伤增量和损伤值分别为

(10)

D1=D0+ΔD1=

(11)

2)N=2时,第2个周期对应的损伤增量和损伤值分别为

(12)

D2=D1+ΔD2=

(13)

3)N=i时,第i个周期对应的损伤增量和损伤值分别为

(14)

D=Di-1+ΔDi=

(15)

则损伤累积为

(16)

损伤增量曲线如图6所示,单循环损伤增量首先在较短的初始疲劳阶段快速大幅下降,在之后的较长时间内保持缓慢的衰减趋势,并在最后的疲劳破坏阶段骤增.由于不同应力水平的α和β存在差异,即加载次序对损伤累积有影响,故该模型的损伤累积具有非线性特征.损伤曲线拟合结果如图6和表4所示,R2>0.96,表明该模型可以对橡胶沥青混合料的损伤演化进行准确的描述.

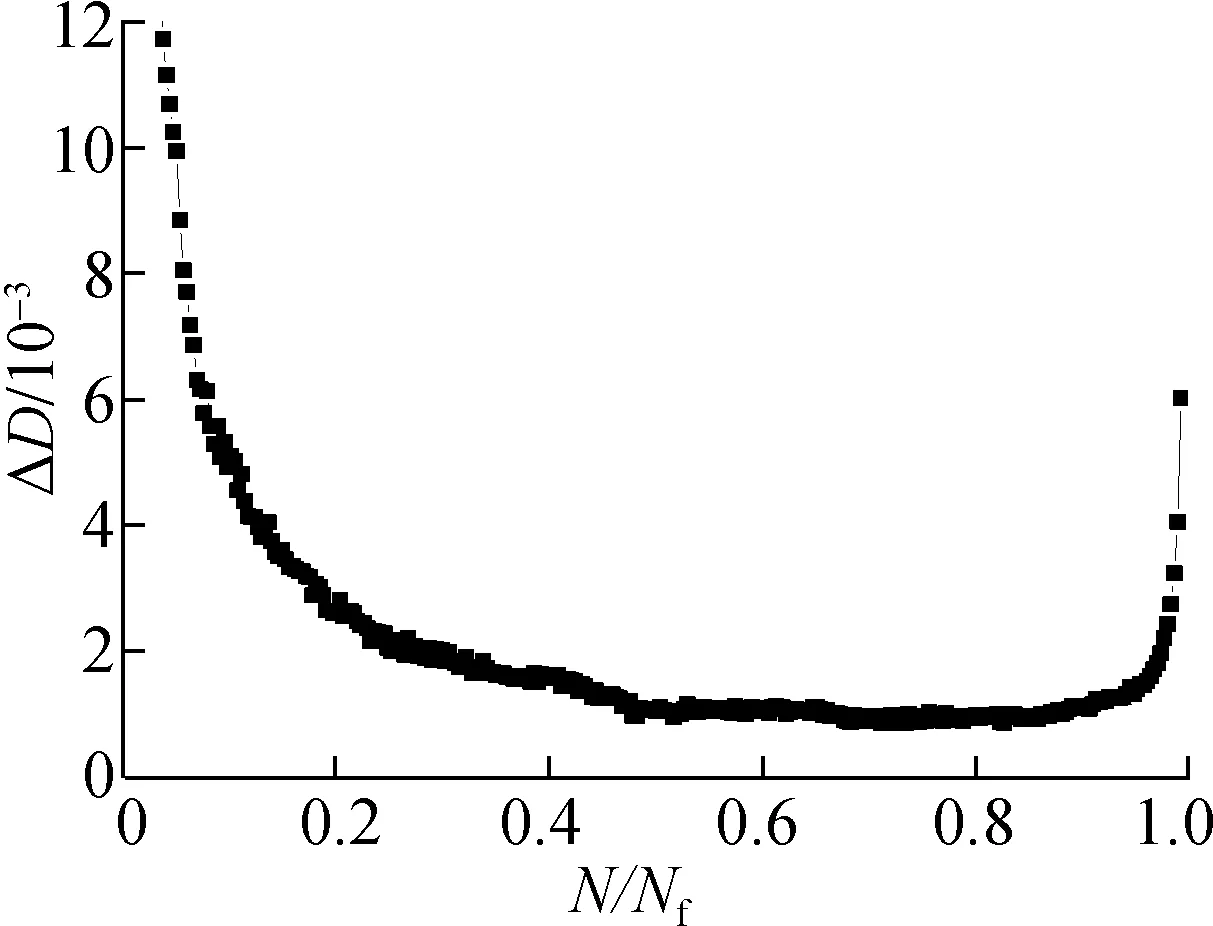
图6 ΔD-N/Nf曲线

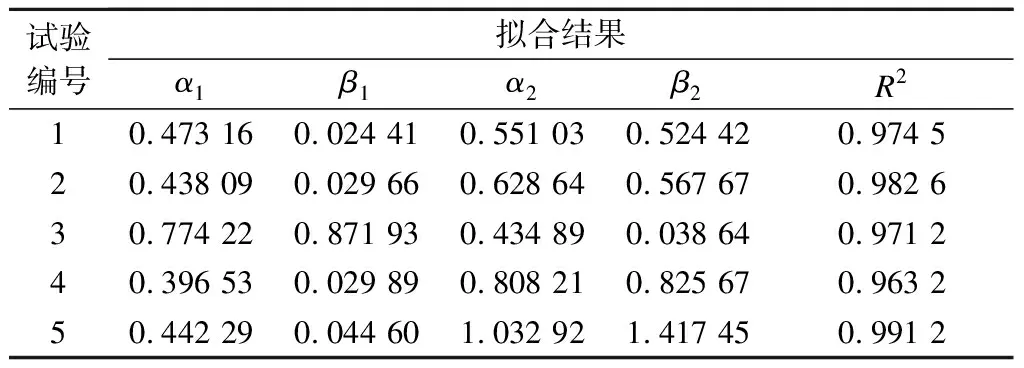
表4 损伤模型结果

3.2 损伤演化分析

橡胶沥青混合料的损伤状态主要由损伤值D、单循环损伤增量ΔD、损伤演化速率Ds反映,D-ΔD-Ds曲线如图7所示.由图可知,Ds和ΔD两者之间线性相关,ΔD和Ds随着D的增大呈相同的三阶段非线性演化趋势.Ds-D-N/Nf曲线如图8所示,由图可知,D在第1阶段快速增加,但Ds逐渐下降,第1阶段比例较小,但D得到较高水平的累积;之后,D缓慢增加,且Ds趋于稳定,第2阶段是整个疲劳过程的主要组成部分;最后,D和Ds均在短时间内骤增,材料结构出现断裂.

图7 D-ΔD-Ds曲线

图8 Ds-D-N/Nf曲线

3.3 疲劳损伤抵抗能力分析

第N次加载的损伤D(N)与第N次加载的损伤演化速率Ds(N)的关系可表示为

(17)

通过分析式(17)可知,剩余疲劳寿命Nfr反映了损伤由初始损伤值Dinit演化至失效阈值对应的疲劳次数,特定条件下的Nfr主要由初始损伤值和Ds两个因素决定[1].预测Nf时,Dinit和Nfr分别为0和Nf,故Nf主要由Ds决定.Nf随Ds的加快而降低,这是因为：随着Ds的加快,沥青混合料整体的疲劳损伤抵抗能力(fatigue damage resistance, FDR)减弱,D越快速地由0非线性地演化至失效阈值,对应的Nf降低,FDR与Nf正相关[6].由图3可知,Nf随着RCDEC的增大而减小,且Nf越接近的2条曲线在空间分布上越接近,故采用RCDEC分析沥青混合料的FDR.损伤演化第3阶段的比例很小,且材料结构已经失稳,在计算 FDR时可以忽略该阶段的RCDEC值.建立的FDR数学模型如下：

式中,RFD为疲劳损伤抵抗能力,等于第1和第2阶段RCDEC的平均值.该公式可用于量化沥青混合料的FDR,统计结果如表5所示,R2>0.96,表明了其可靠性.

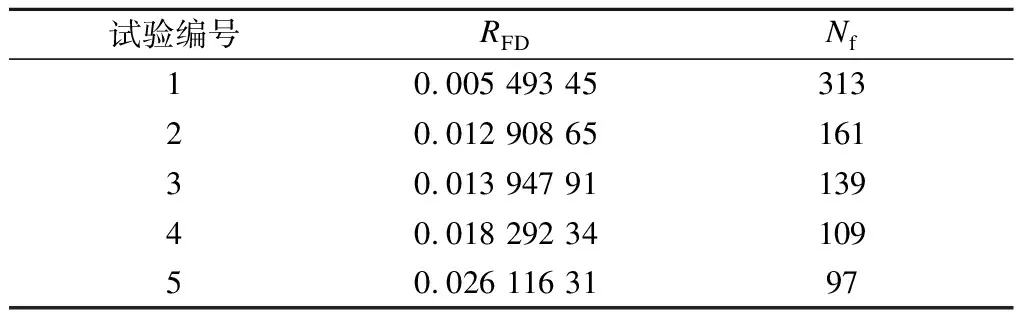
表5 疲劳损伤抵抗能力统计结果

由图3可知,反映FDR的RCDEC分别呈现出快速减小、连续稳定、骤然上升的演化状态,这是因为疲劳荷载作用下材料结构发生重组,较大比例的耗散能在疲劳初始阶段转化为材料损伤.随着材料结构在初始阶段不断发生重组,转化为材料损伤的耗散能比例趋于稳定,该阶段材料具有稳定的FDR.最终,损伤演化速率骤增,材料结构丧失FDR而发生断裂;Nf随着RCDEC的增大而减小,这意味着RCDEC越大的材料其FDR越弱,RCDEC的提高会导致其Ds加快,相应的Nf越小.