壁面展向周期振动的超声速湍流减阻研究
2021-12-23王锁柱刘文伶张立坤
王锁柱,吴 乔,刘文伶,李 强,张立坤
(北京航天长征飞行器研究所,北京,100076)
0 引 言
对于各类飞行器,表面摩擦阻力在总阻力中占有一定的比例,特别是在大气层内长时间高空飞行时摩阻占比较大,提升飞行器性能和节约能源消耗的途径之一是尽量减小表面的摩擦阻力。因此以减阻为目的的转捩和湍流控制因其广阔的应用前景而成为湍流研究的热点。壁面在展向的高频振动是一种有效抑制湍流活性的减阻手段,作为一种主动控制方法,它不需要信息反馈,受到了人们的重视。自20世纪90年代以来,国内外开展了一系列壁面展向振动对壁湍流影响的数值模拟和试验研究。
Jung等[1]首先采用槽道湍流的直接数值模拟(DNS)结果证实了壁面展向振动减阻的有效性,随后Laadhari等[2]采用试验方法进一步证实了该方法的有效性。Choi等[3,4]研究结果表明,壁面展向运动会产生负展向涡,使得流向速度减小并阻碍近壁区域流向涡的拉伸,从而使壁面摩擦阻力显著减小,最大能够达到45%左右的阻力降低。Trujillo等[5]和Bogard等[6]试验研究表明,展向壁面振动可以消除近壁条带结构,从而抑制了上掠和下扫事件的频率,达到减小壁面阻力的效果。
黄伟希等[7]采用DNS研究了壁面展向周期振动的不可压缩槽道湍流,发现湍流受到抑制、壁面摩擦阻力减小,并通过雷诺应力输运方程的分析揭示了压力变形项在湍流抑制中的关键作用,获得的平均壁面减阻率为35%。许春晓等[8]对壁面展向周期运动的槽道湍流进行了大涡模拟,考察了不同亚格子模型对非定常湍流的模拟能力。黄乐萍等[9]同样采用DNS对槽道湍流壁面展向周期振动抑制壁湍流、实现减阻的内在机理进行研究,发现振动引起的涡与条带的倾斜和滑移两种减阻机理交替出现,通过控制参数优化实现的最大壁面减阻率为47.5%。邓飞等[10]在水槽中利用粒子图像测速方法研究壁面展向振动对壁面摩擦阻力及近壁面流场湍流强度的影响,结果表明振动后近壁面的漩涡分布明显较少、速度波动明显减弱,同时减小了脉动速度均方根、消弱了近壁面湍流强度,使近壁面流动趋于层流。
上述研究结果均表明壁面展向周期振动可有效降低壁面摩擦阻力,但这些研究都是针对不可压缩湍流或亚声速可压缩湍流,对于超声速可压缩湍流的研究并不多见。本文针对马赫数为4.5的超声速平板边界层流动问题,采用大涡模拟方法对壁面展向周期振动的超声速平板边界层转捩和湍流进行数值模拟研究,通过对统计定常阶段的分析,研究壁面振动对超声速转捩和湍流的影响规律。
1 物理模型和数值方法
1.1 物理模型
平板边界层流动的计算域和坐标系选取如图1所示。设流体沿平板流动的方向为x,法向为y,展向为z。Lx、Ly和Lz分别为平板沿流向、法向和展向的计算域长度,xin为计算域流向入口位置离平板前缘的距离,即本算例计算域的范围为:xin≤x≤Lx+xin,0≤y≤Ly,0≤z≤Lz,其中y=0表示平板壁面。

图1 平板边界层流动示意Fig.1 Configuration of a Flat-plate Flow
本文采用空间模式对平板边界层的转捩过程和湍流进行大涡模拟,其初始条件包括两部分:一部分是基本的平均流,通过可压缩平板边界层的层流相似性解得到,并设基本流的剖面沿流向不变;另一部分是为了能够使层流发生转捩而在入口引入的扰动,采用了一对等幅值随时空发展的小扰动量[11]。展向采用周期性边界条件,壁面采用等温无滑移边界条件,在流向出口和法向的上边界均为无反射出流条件。
初始的流动和计算参数如表1所示,其中无量纲化所采用的特征量为:参考长度取计算域入口处的边界层位移厚度δd0,参考密度、速度和温度均为自由来流的值。计算网格在展向取均匀分布,沿法向采用双曲拉伸以实现对壁面的加密。
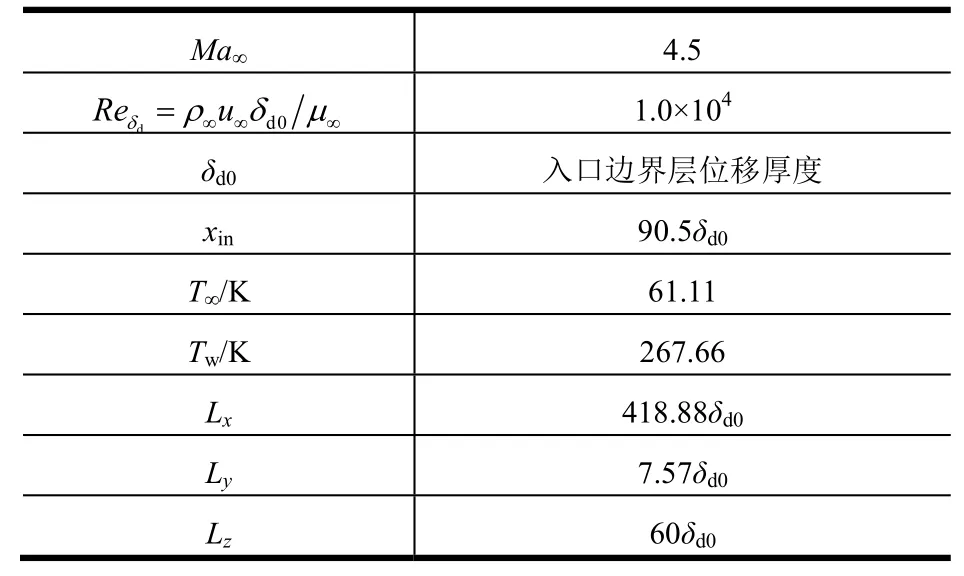
表1 流动和计算参数Tab.1 Flow and Computation Parameters
1.2 大涡模拟方法
本文采用基于Favré过滤的大涡模拟控制方程,为了保证过滤后的能量方程与原始能量方程在形式上一致,便于统一构造计算格式和编制解算器,能量方程采用可解尺度总能形式[12]。亚格子应力项的模化采用已发展的并经槽道湍流模拟验证的动态混合模型[13]:
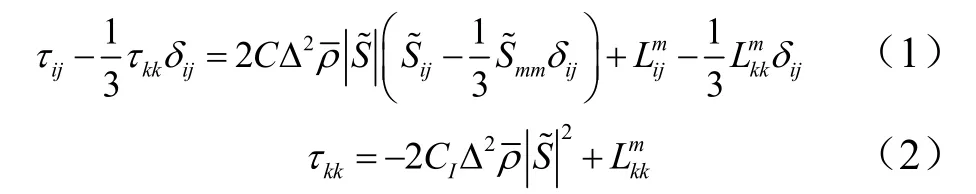
其中模型系数C和CI可基于瞬态流场动态计算得到:
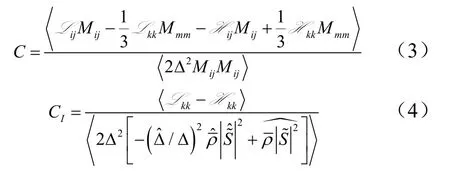
上述公式中具体参数的定义可参考文献[14]。亚格子热通量项采用涡扩散模型:
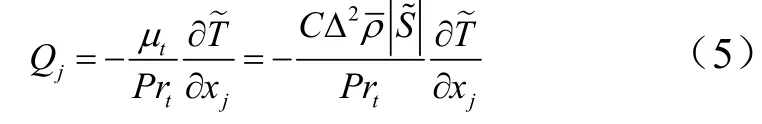
式中Prt为亚格子湍流普朗特数,通常设定为常数。
采用有限差分法对大涡模拟控制方程进行离散求解。对流项经通量分裂后采用五阶迎风型紧致格式[15],粘性项则采用六阶中心型紧致格式[16],时间离散采用满足TVD特性的三阶Runge-Kutta方法。
1.3 壁面振动形式
对于壁面展向振动的形式,几乎所有的相关研究均选择了正弦形式的振动。基于前人的工作,本文研究选用了如下的速度形式:
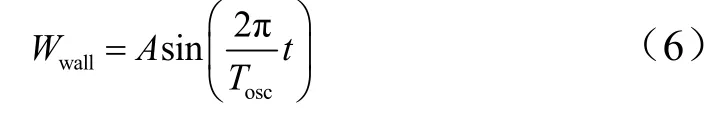
式中A为振动的速度振幅;Tosc为振动的周期;t为时间。在振动过程中壁面温度始终保持不变。为了考察不同振动周期和振幅的影响,选用了5种不同振动参数的算例,具体参数如表2所列。

表2 壁面振动参数Tab.2 Wall Oscillation Parameters
2 结果分析
图2显示了不同算例壁面平均摩擦系数Cf随空间的演化曲线。通过与算例C0的对比可以看出,壁面展向振动对转捩起始位置没有明显影响,但可降低湍流区域的平均摩擦系数,同时导致层流区域的摩擦阻力略有增加。由算例C1、C2和C3的对比可以看出,随着振动周期的增加,湍流区域的减阻效果略有增加;由算例C3、C4和C5的对比可以看出,随着振幅的增加,湍流区域的减阻效果也略有增加。通过与现有文献研究结果的对比可以发现,减阻的总体效果不如不可压缩湍流和亚声速可压缩湍流。
以x=428流向位置处的平均速度和密度加权速度分布为例,如图3所示,可以看到,算例C1~C4的平均速度剖面与C0差别不大;算例C5的结果与C0相比显得更光滑,但所有算例的分布均呈现典型的湍流速度型,说明在此位置上均已进入充分发展湍流阶段。以van Driest变换导出的密度加权速度表示时(图3b),由于壁面摩擦阻力系数的减小添加壁面振动可使对数区的分布曲线上移。
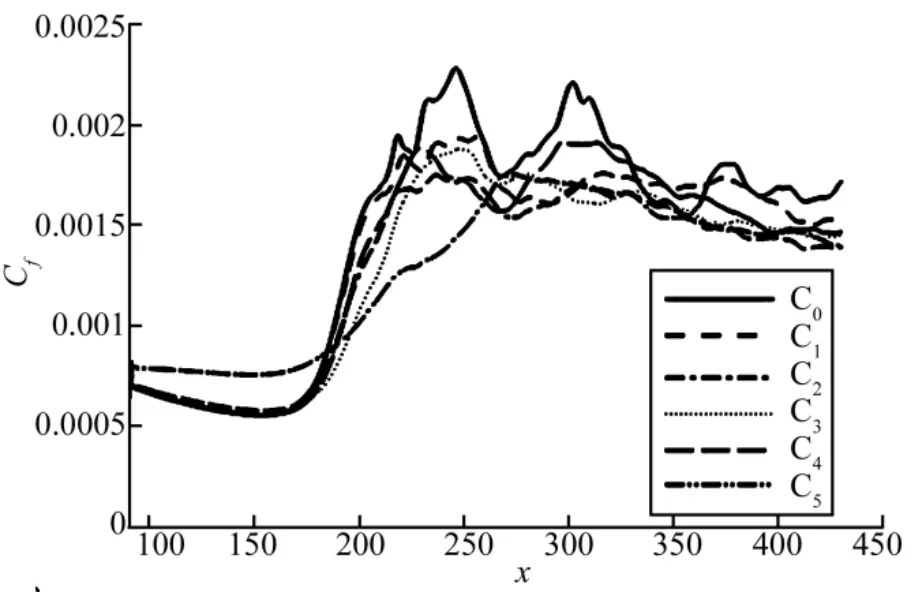
图2 壁面摩擦系数的空间演化曲线Fig.2 Distribution of the Skin Friction Coefficient
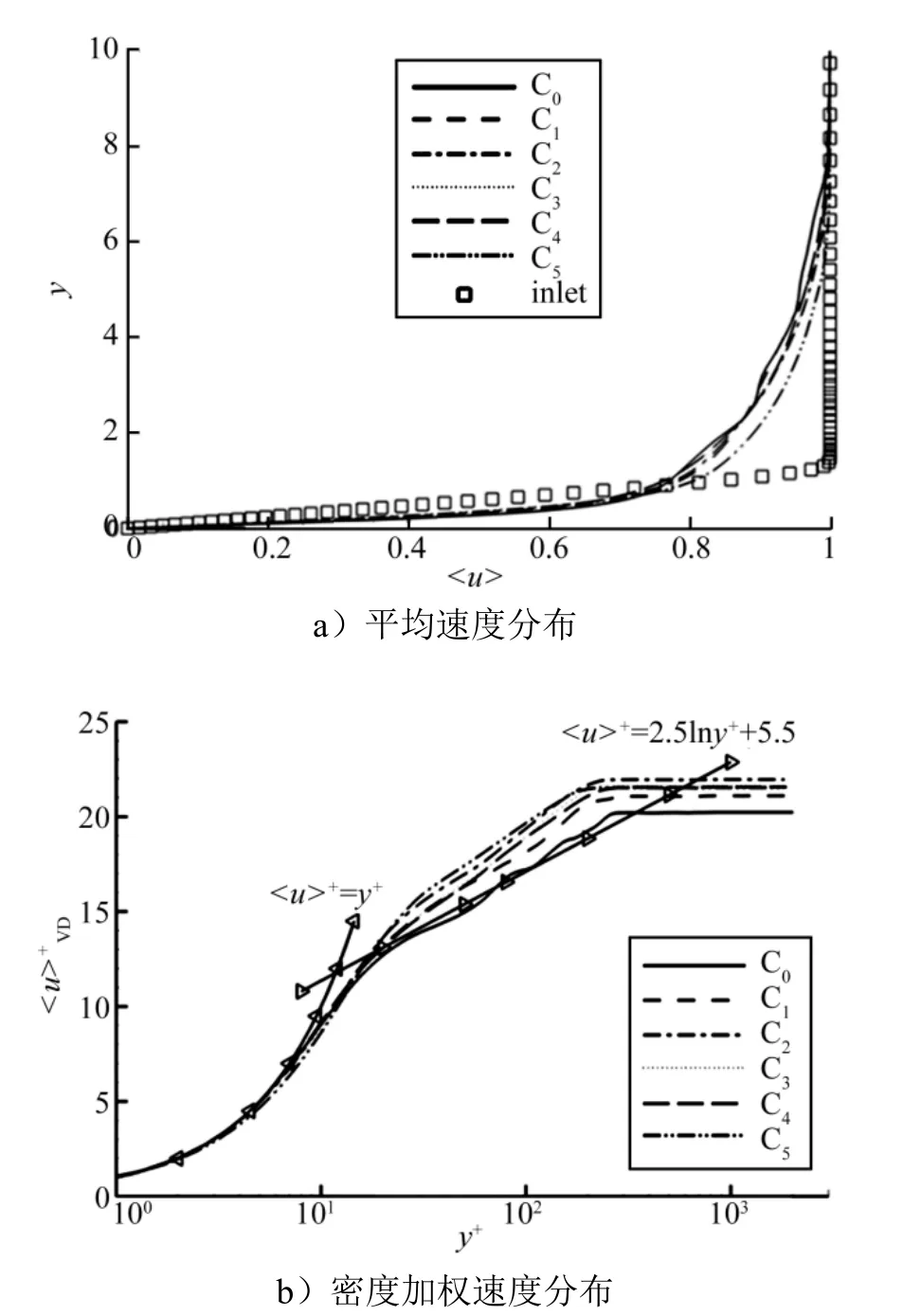
图3x=428流向位置处速度剖面Fig.3 Profiles of the Streamwise Velocity(x=428)
图4给出了x= 428流向位置上的平均温度分布,此时所有算例均进入充分发展湍流阶段,温度分布较为接近,同时从近壁区的放大图可以看出,壁面振动可提高近壁区的温度。图5显示了边界层厚度随流向位置的演化过程。随着振幅和周期的增加,湍流区域的边界层厚度相应减小。
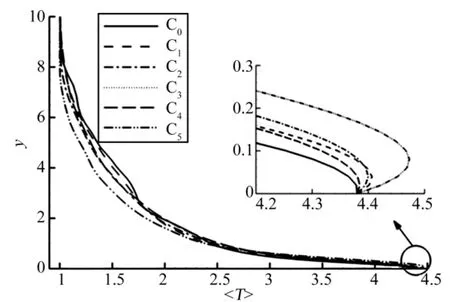
图4x=428流向位置处平均温度剖面Fig.4 Profiles of the Mean Temperature(x=428)

图5 边界层厚度的空间演化曲线Fig.5 Distributions of the Boundary Layer Thickness
图6为x= 428流向位置上湍流马赫数分布,随着壁面振动振幅和周期的增加,分布曲线的峰值以及离开近壁区的分布有所下降,同时峰值出现外移。而近壁区域值的显著增大是由壁面展向振动诱导的展向速度脉动显著增大所致。图7给出了同一流向位置上采用当地摩擦速度无量纲化的流向速度脉动均方根值分布。与湍流马赫数分布相类似,壁面展向振动使边界层内的流向速度脉动均方根值分布整体呈下降趋势,同样峰值也出现外移。通过以上分析可知,壁面展向周期振动能够抑制边界层内湍流脉动的发展。
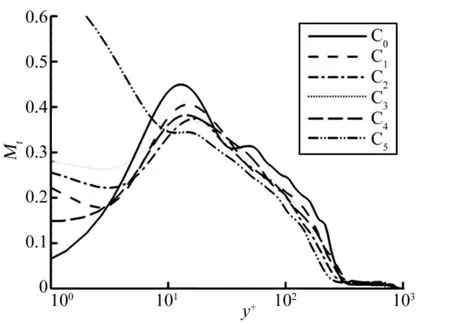
图6x=428流向位置处湍流马赫数分布Fig.6 Profiles of the Turbulent Mach Number(x=428)
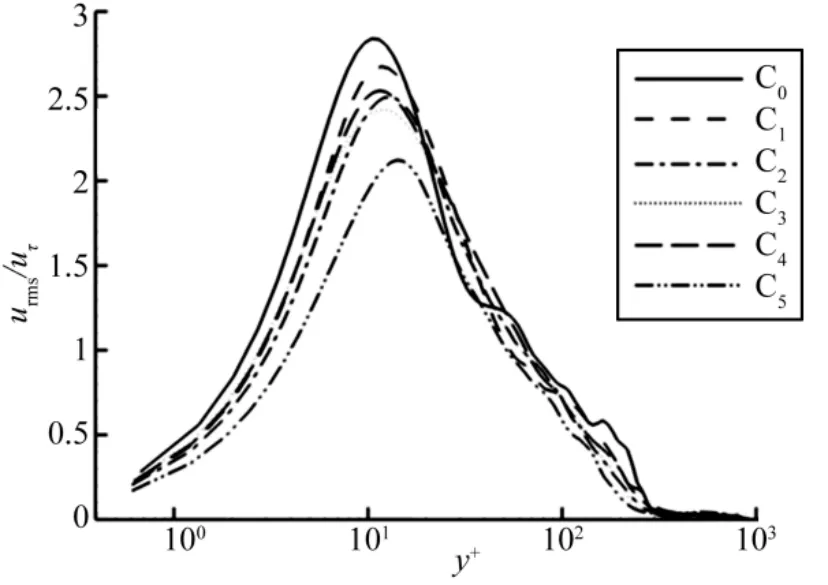
图7x=428流向位置处流向速度脉动均方根分布Fig.7 Profiles of the Rms Streamwise Velocity(x=428)
图8分别显示了算例C4、C3和C5转捩过程中流场涡结构的演化。通过对比可知,随着振动幅值的增加相干结构的生成得到了一定的抑制,相干结构在流场中的密度相应降低,发卡涡和环状涡结构的清晰度也逐步减弱。
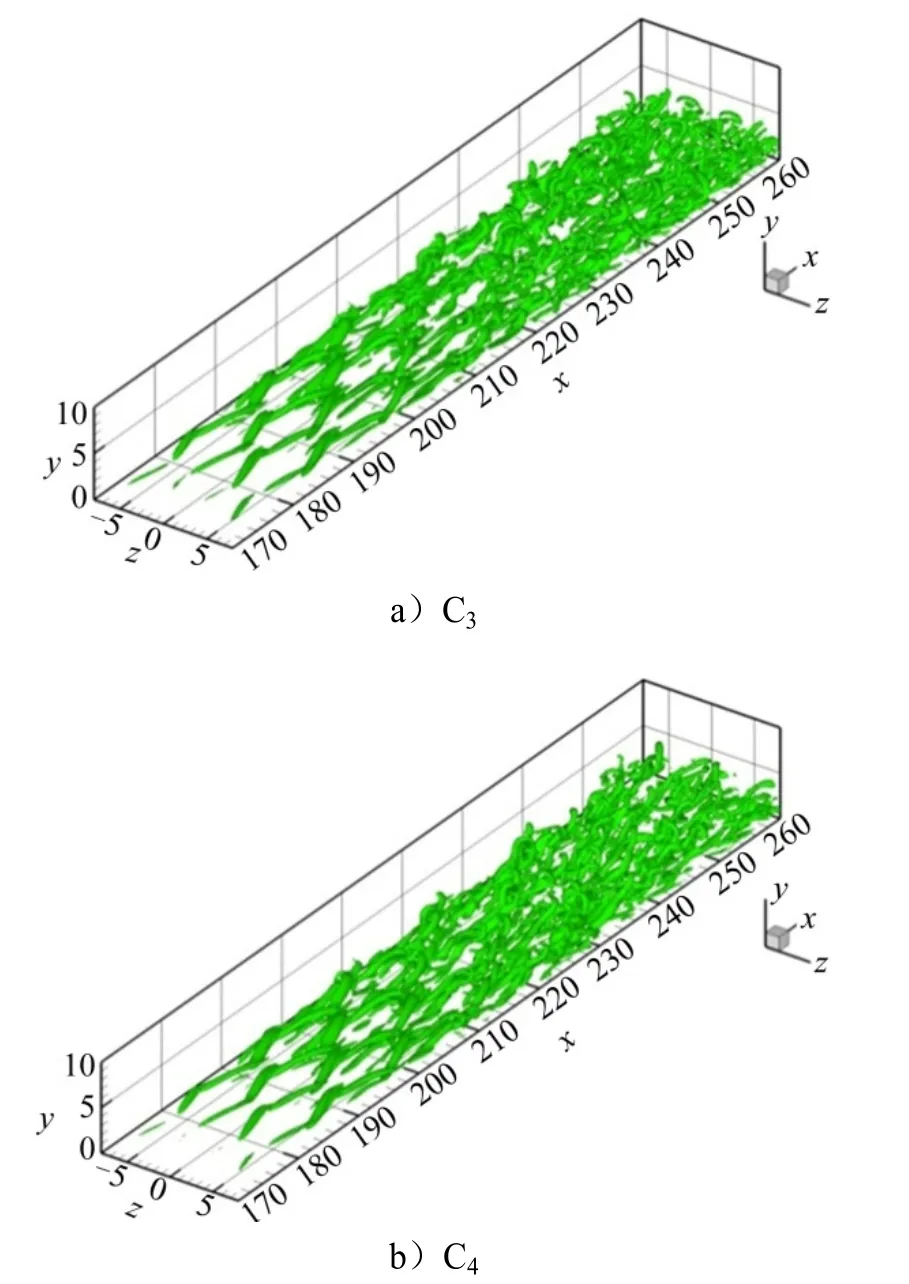
图8 转捩过程中流场涡结构的对比Fig.8 Comparison of the Flowfield Vortex Structure during Transition Process

续图8
3 结束语
本文采用大涡模拟方法对壁面展向周期振动条件下的超声速平板边界层转捩和湍流流动进行了数值模拟研究。通过不同振动幅值和周期结果的对比分析发现,对于超声速平板边界层流动壁面展向周期振动无明显延缓转捩的趋势,但可减小湍流区域的壁面摩擦系数,但效果没有不可压缩湍流和亚声速可压缩湍流明显。此外,展向周期振动对边界层内湍流脉动的发展也具有一定抑制作用,在一定程度上抑制了流场相干结构的生成,削弱了流场相干结构的密度。
