Exploration of magnetic field generation of by direct ionization and coherent resonant excitation∗
2021-12-22ZhiJieYang杨志杰QingYunXu徐清芸YongLinHe何永林XueShenLiu刘学深andJingGuo郭静
Zhi-Jie Yang(杨志杰), Qing-Yun Xu(徐清芸), Yong-Lin He(何永林), Xue-Shen Liu(刘学深), and Jing Guo(郭静)
Institute of Atomic and Molecular Physics,Jilin University,Changchun 130012,China
(Received 8 March 2021;revised manuscript received 11 May 2021;accepted manuscript online 20 May 2021)
Keywords: ultrafast magnetic field generation, electronic ring current, coherent resonant excitation, direct single-photon ionization
1. Introduction
To explore quantum dynamics by using ultrafast laser pulses on its intrinsic time scale is an area of current interest.The rapid development of the techniques of attosecond pulse generation, has become an important tool for investigating electronic dynamics on its natural attosecond time scale and sub-nanometer dimension. And it also promotes the development of some optical imaging technologies,such as Coulomb explosion,[1,2]laser-induced electron diffraction.[3–6]Now the shortest 43-as pulses can be used for new ultrafast optical imaging.[7]Ultrafast negative charge migration illustrates the electron dynamics on attosecond time scale, which is a fundamental quantum process in many biological and chemical reactions.[8,9]This process can be used for selective laser excitation in molecules.[10,11]Besides,coherent superposition of electronic states leads to an electronic ring current inside the molecule,[12,13]which is of latent applied value on molecular magnetism and can be used as a new source of ultrafast magnetic field. Recent experiments demonstrate that people can precisely manipulate the spatial distribution of currents in the semiconductor and subsequently control the ultrafast magnetic field generation.[14]Exploring the time-dependent ultrafast magnetic field that depends on the electronic coherence may provide a direct way to access and control the electronic quantum coherence dynamics in photophysical and photochemical reactions in real time. Optically induced magnetic fields are also used as tools for investigating new phenomena in molecular and material sciences.[15–19]Now a lot of researches have shown that the ultrafast magnetic fields can be efficiently produced in molecules from electronic ring currents.[20,21]Results show that the laser-induced magnetic fields generated by electronic currents are static and can be much larger than those obtained by traditional methods about static field.[22]Therefore,it is of great significance to the development of molecular magnetism. However,most of researches has been focused on linear molecular systems and single electronic state processes.

2. Theoretical method


The circularly polarized laser pulse is used to investigate the electron dynamics in molecules.[20,23,25]The interaction between the electron and the laser pulse isr·E(t)=xEx(t)ˆex+yEy(t)ˆeyunder the length gauge and dipole approximation in the (x,y) plane. The expression of the circularly polarized laser pulse is as follows:

which propagates along thezaxis with polarization direction ˆexand ˆeyin the (x,y) plane. A sin2(πt/nT0) envelopef(t) is adopted, whereT0=2π/ωis the optical cycle (o.c.).This pulse satisfies the total zero area∫E(t)dt=0.[26]The 2D TDSE in Eq. (1) is numerically solved by a second-order split-operator method combined with fast Fourier transform(FFT)technique.[27,28]The time step is fixed at ∆t=0.01 a.u.(1 a.u.=24 as)and the spatial steps are ∆x=∆y=0.25 a.u.(1 a.u.=1a0). The total spatial length is 128 a.u. The cos1/8mask function is used to suppress unphysical effects generating from the reflection of the wave packet from the boundary.And the absorption boundary is set to|x,y|=40 a.u.

Fig. 1. (a) molecule oriented in the (x,y) plane. Si (i=1, 2, and 3)denotes the s orbital of the atomic H on proton i. R is the distance between two protons and the bond angle Θ =60◦. (b)The A′ electronic state of molecule calculated by imaginary-time evolution method. (c)Illustration of the A′ orbital of molecule obtained by Gaussian09.
The quantum expression of the time-dependent electronic current density in the length gauge can be written as[29,30]

wheretr=t −r/cis the retarded time andµ0=4π×107NA−2(6.692×10−4a.u.). For the static-induced magnetic field after the laser pulse, equation (5) reduces to the classical Biot-Savart law.[31]
3. Results and discussion

In Figs. 3(a) and 3(b), we display the density distributions of the electron wave packet around the peak of pulse.From Fig. 3(a) one sees that the electron is localized and the coherent electron wave packet moves counterclockwise among the three protons periodically. The duration of one cycle is aboutT0=1000 as, approximately equal to one cycle of the laser field with 300 nm. Besides, the electron density distribution presents symmetric structures onyaxis at timet=5.25 o.c., 5.75 o.c., and asymmetric structures onyaxis at timet=5.0 o.c.,5.5 o.c.,6.0 o.c. However,from Fig.3(b)one sees that the electron density distribution maintains a symmetric structure,which do not depend on the time.
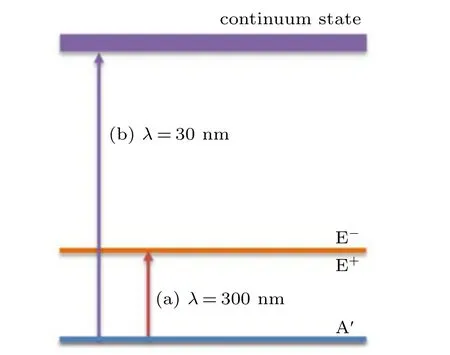
Fig. 2. Illustration of resonance excitation and direct ionization in our scheme: (a)the coherent resonant excitation arises between A′ state and E+state in molecule by λ =300 nm (ω =0.152 a.u.) circularly polarized laser pulses;(b)the direct ionization from the A′ state to the continuum state after one-photon absorption by a circularly polarized laser pulse with wavelength λ =30 nm(ω =1.52 a.u.).
The circularly polarized pulse with the wavelength ofλ=300 nm,leads to the charge migration from A′state to E+state. A coherent resonant excitation between the two electronic states arises after one-photon absorption which leads to a coherent superposition state. The resulting coherent superposition state wave function can be represented as[32]

where ∆E=EE+−EA′is the energy difference between the A′state and E+state.The interference termA(A′,E+)(r,t)is timedependent,which describes the attosecond coherent electronic migration.[33]The oscillation period of the interference term is ∇τ(0)=2π/∆E=T0. Thus, the time-dependent coherent electron density distributions depend on the interference term of the A′state and E+state. At ∆Et=nπ,t=nT0/2,wherenis an integer,the interference term cos(∆Et)=±1 leads to the maximum asymmetric structures of the electron density distributions,whereas at ∆Et=(n+1/2)π,t=(n+1/2)(T0/2)and cos(∆Et)=0,symmetric structures are produced,as shown in Fig.3(a). For the direct single-photon ionization,the electron is ionized from the A′state to the continuum state by absorbing one-photon. Thus, the coherent superposition state does not exist anymore. As a result, the electron density distributions cannot be influenced by the coherent effects,so it present a symmetric structure,which do not depend on the time,as illustrated in Fig.3(b).
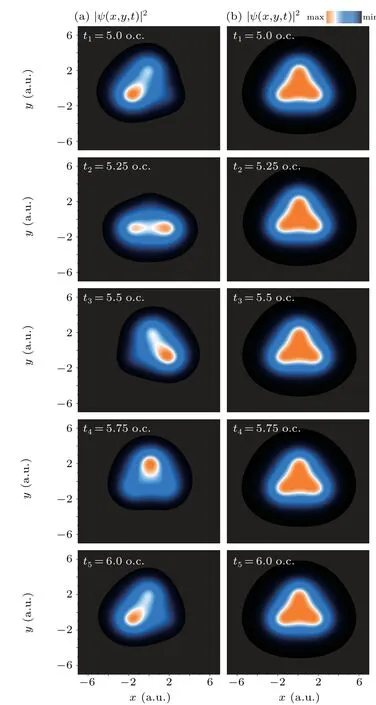
Fig. 3. Density distributions of the electron wave packet p(x,y,t) =|ψ(x,y,t)|2 in the (x,y) plane at different moments ranging from t = 5T0 to 6T0: (a) the coherent resonant excitation and (b) the direct single photon ionization.
Based on the evolution of the electron density distributions, we further investigate the induced electron ring current inside molecules. We show the distributions of the induced electronic current densitiesj(r,t) at various moments in Figs. 4(a)–4(b). The white arrows represent the directions of the electronic currents.In Fig.4(a)for the coherent resonant excitation case,we see that the induced ring electronic current evolves counterclockwise with a period ofT0=1000 as. Besides,the evolution of the electronic current is approximately in phase with the rotation of the coherent electron wave packets. It is shown that the time-dependent electron current produced in charge migration attributed to the periodical evolution of the coherent electron wave packet between the protons.In Fig. 4(b) for the direct single-photon ionization case, we see that the ring current also evolves with a counterclockwise direction. The period isT0=100 as. And the structure of electron current density is similar as that of the electron density distribution in Fig.3(b).

Fig.4. The electronic current distributions for different times ranging from t =5T0 to 6T0. The white arrows label the directions of the electronic currents. (a) The coherent resonant excitation and (b) the direct single-photon ionization.
In order to better observe the variation of electron current with time, we investigate the electronic currents by integratingj(r,t) over the section fromr=0 tor=∞. Since the electronic current is continuous,the probability of the electron currents being measured through any cross sections originated from the center point are equal.[21]The integral equation of Eq.(4)along thexaxis can be written as[34]

wherej(r,t)=jx(r,t)ˆex+jy(r,t)ˆeyand ˆex,yare the unit vector alongxandydirections. As shown in Figs.5(a)and 5(b),the electronic currentsJ(t) oscillate periodically with timetresembling a cosine function and the oscillation period is about one optical cycle. Moreover, the change in intensity of the electronic currents with time is approximated in phase with the amplitude change of the driving pulse. It is shown that the intensity of the electronic currents is sensitive to the amplitude of the driving pulse. In Fig.5(a)we can see that for the coherent resonant excitation case,the intensity of the induced electronic current reaches the maximum value 0.0195 a.u. at 5.0 o.c. Of note is that after the pulse being switched off(t>10 o.c.), the weak electronic current still exist and oscillates with a periodT=0.67T0. According to the coherence of electron wave packets, the coherent electron wave packets still spread spatially after the pulse being switched off and its quick spread results in a shorter oscillation period of induced electronic current, compared with the case of the pulse being switched on. In Fig. 4(b) for the direct single-photon ionization case, we find that the intensity of the induced electronic current also reaches its maximum value 0.0015 a.u. at 5.0 o.c.However, the electronic current will not exist after the pulse being switched off since there is no coherent electron wave packet.
In Figs. 5(a) and 5(b), we label the five momentst1–t5which corresponds to the Figs.4(a)and 4(b)with red crosses.From five moments in Fig.5(a),one can see that the value of the electronic current is positive att2=5.25 o.c.,t3=5.5 o.c.,
whereas it is negative att1= 5.0 o.c.,t4= 5.75 o.c.,t5=6.0 o.c. Att2=5.25 o.c. andt4=5.75 o.c., the intensity is close to 0. From five moments in Fig. 5(b), one can see that the value of the electronic current is positive att1=5.0 o.c.,t4=5.75 o.c.,t5=6.0 o.c.,while it is negative att2=5.25 o.c.,t3= 5.5 o.c. Similar as that in Fig. 5(a), the intensity of the electronic current is also close to 0 att2=5.25 o.c. andt4=5.75 o.c. The direction of electronic current are different in two cases at timet →t+T0/2 as illustrated in Figs. 4(a)and 4(b). The results show that the induced electronic currents oscillate periodically with different phases in two cases and the intensity of the coherent resonant excitation case is approximately one order of magnitude larger than that of direct ionization case. Since the electrons are ionized to the continuum state for the direct single-photon ionization case, the induced electronic current mainly comes from the free electrons in the continuum state,thus leading to a weak electronic current inside the molecules. And the oscillation of the electronic current is affected by coherent electron wave packet for case of the coherent resonant excitation.
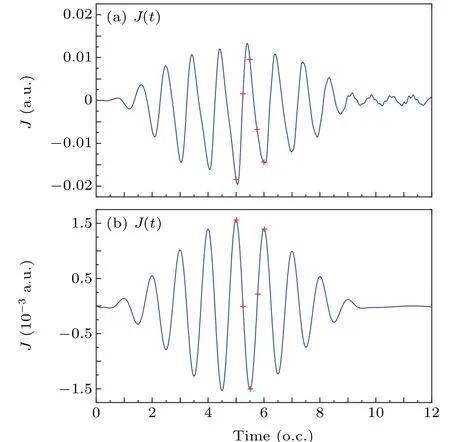
Fig.5.Illustration of the time-dependent electronic currents for two cases(a)the coherent resonant excitation and (b) the direct single-photon ionization,the red crosses label five moments t1=5.0 o.c.,t2=5.25 o.c.,t3=5.5 o.c.,t4=5.75 o.c.,t5=6.0 o.c.respectively.
The induced time-dependent electronic current can generate an internal ultrafast magnetic field in the molecule. In Figs. 6(a) and 6(b), we display the time-dependent magnetic fieldsB(r= 0,t) at the molecular center generated by the electronic currentsj(r,t), which are shown in Figs.5(a)and 5(b). According to classical physics,[35]the direction of generated magnetic fields mainly along thezaxis, perpendicular to the (x,y) plane. The generated magnetic field also has dependence on the molecular orbitals. Figures 6(a) and 6(b)show the generation of magnetic fields with different intensities and phases at every nuclear centers. Due to the spiral effect of the circularly polarized laser pulse,the generated magnetic fields at every nuclear centers are not equivalent. The magnetic fieldB(r=0,t)at the molecular center arises from the electron current, which is determined by the coherent superposition of the wavefunctions of the three protons. It is found that the time-dependent magnetic fields oscillate periodically with a periodT0, which indicate the electron coherence of the currents. As shown in Figs. 6(a) and 6(b), one can see that the oscillating magnetic field still exist after the pulse being switched off for the case of coherent resonant excitation, whereas the magnetic field does not exist anymore after the pulse being switched off for the case of direct singlephoton ionization. The evolution of the magnetic field can be predicted by the induced electronic currents as illustrated in Figs.5(a)and 5(b), confirming the coherence of the electron.The results show that for the coherent resonant excitation the enhanced magnetic fieldB(r=0,t)has the maximum value 0.27 T, whereas for the direct single-photon ionization case the maximum value is 0.015 T.The difference of the magnetic fields about two cases is associated with the electronic currents,and is also dependent on the photoionization process in molecules. Consequently,one can control the magnetic fields by adjusting the laser parameters. And the photoionization process encoded in the electron currents can be reconstructed with spatial and temporal resolutions by generated magnetic fields.

Fig. 6. Illustration of the time-dependent magnetic fields at the molecular center r=0 and the three molecular proton centers, generated by the electronic currents corresponding to those in Figs.5(a)and 5(b)for(a)the coherent resonant excitation and(b)the direct single-photon ionization.
4. Conclusion
We use the triatomic molecule with cyclic geometryas a benchmark system to investigate the induced electronic current and the generation of ultrafast magnetic field. Results from numerical solutions of the molecular TDSE show that the induced electronic currents and the generated magnetic fields depend on the photoionization process of molecules in intense laser fields. We calculated the electronic current and magnetic field in two cases: the coherent resonant excitation and the direct single-photon ionization. The circularly polarized pulses with wavelengthsλ=300 nm andλ=30 nm are adopted respectively. For case of the coherent resonant excitation, with the asymmetric distributions of the coherent superposition as functions oft, the enhanced electron current arises subsequently, leading to the enhanced magnetic field generation. Moreover, the periodical evolution of the coherent electron wave packet leads to the fact that the electronic current oscillates periodically, which can produce oscillating magnetic fields. For the direct single-photon ionization, the electron is ionized from the A′state to the continuum state by absorbing one-photon. So,the coherent superposition state does not exist anymore. Since the induced electronic current mainly comes from the free electrons in the continuum state,it can generate a relative weak magnetic field. The results show that both the electronic current and the magnetic field have different phases in the two cases. Moreover, the intensity of the coherent resonant excitation case is approximately one order of magnitude larger than that of direct ionization case. One can modulate the electronic current and the magnetic field by adjusting the parameters of the driving field. So,exploring the photoionization process in molecules is essential for controlling of the electronic current and the ultrafast magnetic field in molecule. In principle, our work can be used to explore the electronic dynamics in ring-molecules systems,presenting a general scheme which can also suitable for different atoms and molecules,and this scheme has great potential for ultrafast magnetism and electron dynamics.
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Modeling the dynamics of firms’technological impact∗
- Sensitivity to external optical feedback of circular-side hexagonal resonator microcavity laser∗
- Controlling chaos and supressing chimeras in a fractional-order discrete phase-locked loop using impulse control∗
- Proton loss of inner radiation belt during geomagnetic storm of 2018 based on CSES satellite observation∗
- Embedding any desired number of coexisting attractors in memristive system∗
- Thermal and mechanical properties and micro-mechanism of SiO2/epoxy nanodielectrics∗
