Dependence of photoelectron-momentum distribution of H+2 moleculeon orientation angleand laser ellipticity*

Hong-Dan Zhang(张宏丹),Si-QiZhang(张思琪),Lei Ji(纪磊),QiZhen(甄琪),

Jing Guo(郭静)1,†,and Xue-Shen Liu(刘学深)1,‡

1Institute ofAtomic and MolecularPhysics,Jilin University,Changchun 130012,China

2SchoolofPhysicsand Electronic Technology,Liaoning NormalUniversity,Dalian 116029,China(

Received 15 February 2019;revisedmanuscript received 7March 2019;published online22 April2019)

Keywords:H+2 molecule,molecular photoelectron-momentum distribution,attosecond perturbation ioniza

1.Introduction

The rapid development of ultrashort laser pulses offers the possibility for investigating electron dynam ics on its natural attosecond(1 as=10-18s)time scale.[1–5]Attosecond pulses allow us to separate electronic(attosecond time scale)and nuclear(fem tosecond time scale,1 fs=10-15s)effects.Thus,one can study electronic dynam ics regardlessof the interference from nuclear motion.The attosecond pulse can be obtained by superposing some orders from high harmonic generation.[6,7]To date,the shortest single attosecond soft-xray pulse of 43 as has been obtained by Gaumnitz et al.[8]One can thuswatch pure electronic quantum effects through attosecond imaging.[9]

Ultraviolet(UV)laser pulses have been used as a powerfuland eff icient tool for the research on electron dynam ics.The attosecond extreme ultraviolet(XUV)transient absorption spectroscopy has been w idely applied tomany ultrafast dynam ical processes,including themeasurement of valence electrons,[3]thestudy ofautoionizationofatoms,[10]and probing the time-dependentmolecular dipoles.[11]Ithasalso been employed as a probing pulse in the real-time probing of the electron dynam ics of an atom.XUV probing can also be applied to explore the excitation dynam ics during and after the infrared(IR)pump pulse interaction.[12]

The research on the simplest H+2molecule providing an ideal prototype for diatom ic molecules has attracted much attention,and it has been served as a vehicle to understand and explore some basic physical processes such as high harmonic generation,[13–16]the double-slit interference effect,[17,18]the dissociation of H+2molecule,[19,20]and the photoionization[21–23]and photoelectron-momentum distribution(PMD).[24–26]

Thestrong f ield electronem ission from H+2hasbeen studied experimentally.Odenweller et al.[27]found that the observed unexpected time instants and initial velocities for the electron emission are due to a complex electronicmotion inside H+2.Themolecular photoelectron-momentum distribution(MPMD)by bichromatic circularly polarized attosecond UV laser pulse has been theoretically studied,and the MPMDsexhibitaspiralstructure forboth co-rotating and counterrotating schemes.[28]We researched the sensitivity ofMPMD and molecular photoelectron angular distribution(MPAD)of H+2to internuclear distance,laser ellipticity,as well as the wavelength.In addition,laser-induced electron diffraction(LIED)[21]occurred when the wavelength is changed from 35 nm to 5 nm.[29]Guan et al.[30]theoretically investigated themultiphoton ionization of H+2irradiated by ultrashort elliptically polarized laserpulse forchanging centralphoton energies and they found that the conf inementeffectobserved in linearly polarized laser pulse still exists in elliptically polarized laser pulse.The effectof Coulomb potential on MPMD has been investigated by screening the Coulomb potential at different radii based on classical trajectory calculations and it presents a picture of how the trajectories are bent by the Coulomb potential.[31]The research on MPMD is not constrained within H+2.Some studies aimed atmolecular orbital imaging viaMPMD of N2,CO2,and so on.[32]

In this paper,we investigate the MPMD of H+2under elliptically polarized laser pulse.TheMPMDsexhibitdifferent patternsundervaryingorientationanglesand laserellipticities.We use the attosecond perturbation ionization theory and the exactly solvablephotoionizationmodel to quantitatively interpret the variation of MPMDs along with differentorientation anglesand laser ellipticities.The evolutions of electron wave packet(EWP)and MPMD arealso presented to furtherexplain thedistinctpattern ofMPMD for theellipticityε=0when H+2is f ixed along the x-axis.

2.Theoreticalmodel

We considera f ixed nucleiH+2with differentorientations exposed to the elliptically polarized laser pulse with varying ellipticities.The two-dimensional(2D)time-dependent Schr¨odingerequation(TDSE)under the frozen-nucleiapproximation is

The atom ic units(a.u.)are used throughoutunless stated otherw ise.The soft-core Coulomb potential can be expressed as

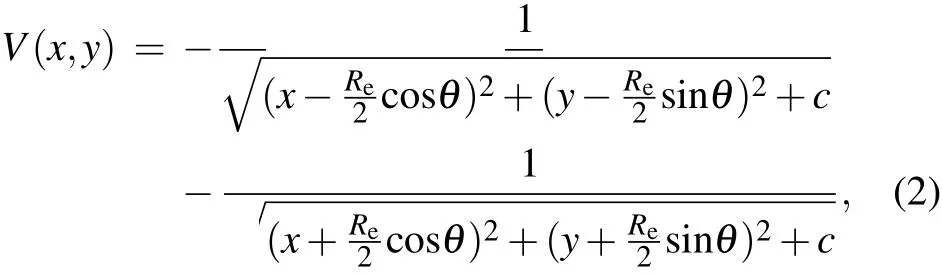
where Re=2 a.u.is the equilibrium internuclear distance,c=0.5 is the soft-core parameter which is chosen to obtain the ionization potential of H+2molecule,θis the orientation angle between themolecular axis and the x-axis,Ex(t)and Ey(t)are the x and y componentsof the laser f ield,and pxand pyare themomentum operators in the x-and y-direction.

This research is based on solving 2D TDSE by the splitting-operator fast-Fourier transform algorithm.[33]The initialwave packet can be constructed by propagating an initial appropriate wavefunction in imaginary time.The spatial coordinates are discretized by the grid points extending from-204.8 a.u.to 204.8 a.u.containing 1024 grid points in both x-and y-directions.During the calculation,thewave packets are multiplied by a cos1/8mask function in each step to suppress the non-physical ref lection at the boundaries.The absorber domain in both x-and y-directions range from 150 a.u.to 204.8 a.u.At the f inal propagation time,the wave packet ismultiplied by amask function M(r)thatsplits the wave packet into ionized part and bounded part.[34]The MPMD can be obtained by Fourier transforming the ionized wave packet.Another four optical cyclesare propagated after theend of the laserpulse to collect the“slow”photoelectrons.TheMPMDsare convergedwith respect to the f inal time.

3.Resultsand discussion

Theelliptically polarized laser f ield in oursimulation is

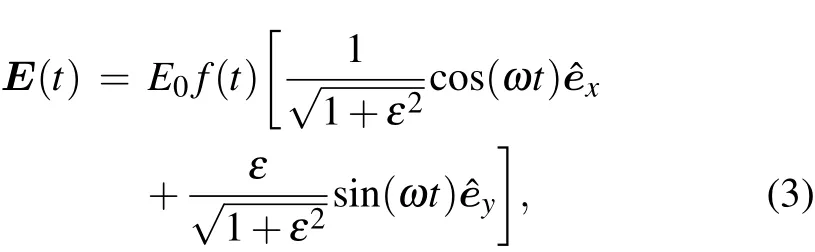
whereω=1.52 a.u.(λ=30 nm)is the laser angular frequency,E0=0.12 a.u.(I0=5×1014W/cm2)is the maximum f ield strength of the laser f ield,εis the ellipticity of the laser f ield,and f(t)=sin(πt/nT)2is the laser envelope;the pulse lasts for 10 optical cycles(n=10).In our calculation,the single-photon process is considered which means that the electron can be ionized by absorbing only one photon(ω＞Ip=1.1 a.u.).

Figure 1 shows the molecular Coulomb potential and MPMD with differentorientation anglesand laserellipticities.Itcan be seen from Figs.1(d)–1(f)and Figs.1(g)–1(i)that the MPMDs withε=0.5 andε=1.0 are all localized mainly in two parts,and the distributions are all perpendicular to the molecular axiswith relative small tilted angles which come from the effect of Coulomb potential and the helicity of the laser f ield.[27,35]Our previous theoretical research(calculated by 30 nm laser pulse)[29]has shown similar distribution pattern with thatunder the experimental result(by 800 nm laser pulse).[27]The classical analysis has also verif ied the effect of Coulomb potentialon the distortion ofMPMD,and the research shows that the tilted anglewould increase as the laser intensity increases.[36]

The orientation effect on MPMD has previously been studied.[37]These authors researched the orientation of H+2molecule relative to the plane of laser polarization within three-dimensional system by the 800 nm few-cycle highintensity near-infrared circularly polarized laser f ield and their resultsshowed asignif icantimpactoforientationon thePMDs due to the anisotropicmolecular potentialand the orientationdependent coupling between the ground state and excited states.In our calculations,we choose the 30 nm attosecond UV laser f ield with varying ellipticity to study the orientation dependenceofH+2molecule in the laserpolarization plane within 2D system.

Our results can be explained well by the attosecond perturbation ionization theory[38,39]and theexactly solvable photoionizationmodelof H+2using theδ-function pulse.[21,23,29]

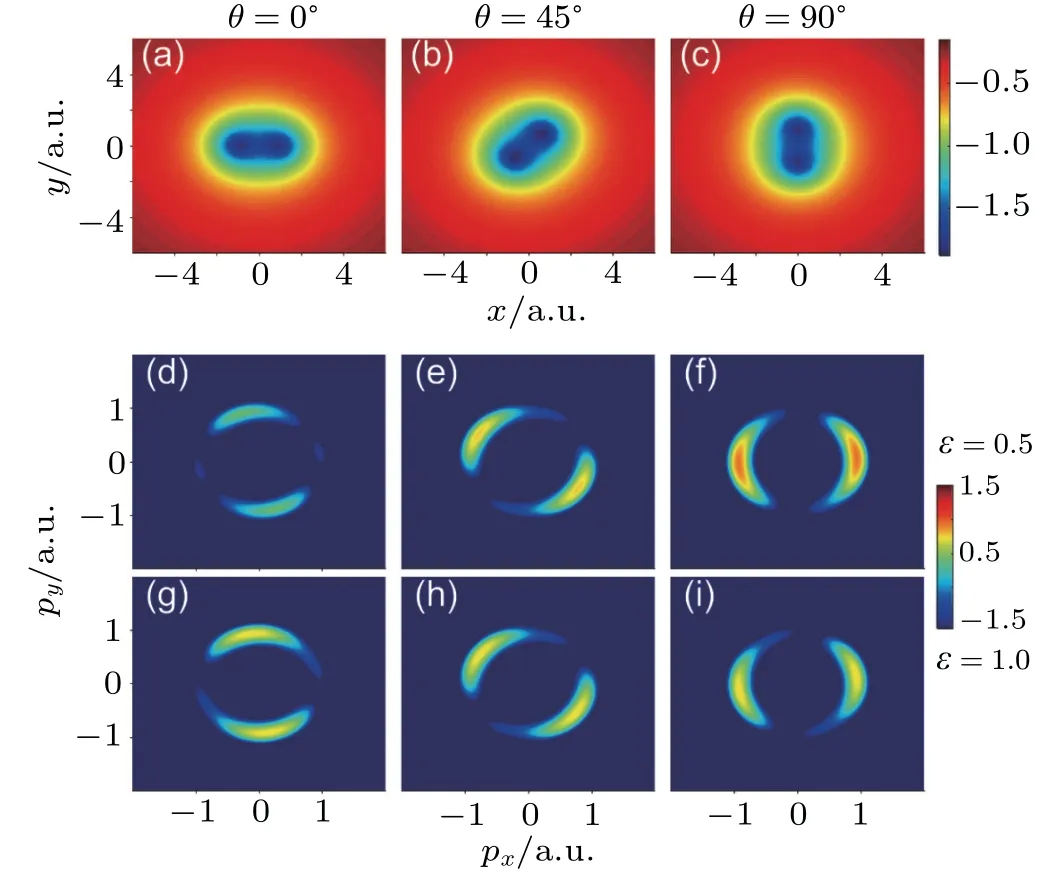
Fig.1.Coulomb potential of H+2 with different orientation anglesθ and MPMD of H+2 with differentθand ellipticitiesε.The f irst column,i.e.,(a),(d),and(g),is for the caseofθ=0°;the second column,i.e.,(b),(e),and(h),is for the case ofθ=45°;the third column,i.e.,(c),(f),and(i),is for the case ofθ=90°.The f irst row(a)–(c)is the Coulomb potentialwith threeorientation angles,and the intensitiesare on a linearscale;the second row(d)–(f)is theMPMDwithε=0.5(elliptically polarized laser f ield),and the third row(g)–(i)is the MPMD withε=1.0(circularly polarized laser f ield),the intensities are on a logarithm ic scale.

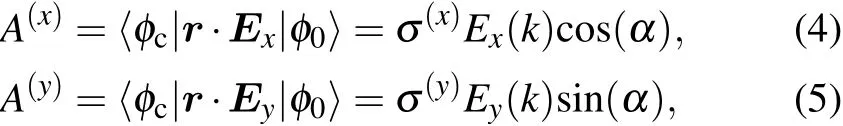
Thesingle ionization amplitude can bew ritten as whereσ(x)=〈φc|x|φ0〉andσ(y)=〈φc|y|φ0〉are the transition matrix elements along the x and y directions,αis the angle between the photoelectron momentum p and the x-axis,|φ0〉and|φc〉are the initial ground state and continuum state,respectively,andandare the pulse frequency shape as a Fourier transform of the pulse along the x and y directions,wheret and Ey0(k)=

∫∞

-∞E0f(t)sin(ωt)eiktd t.The totaldistribution reads

where the interference term is

For H+2with two centers,the corresponding MPMD is the superposition of ionization from the two nuclei.According to the exactly solvable photoionization model of H+2by δ-function pulsewhich has described LIED in ultrafast laser f ields before,[21]the wavefunction inmomentum space right after the pulse is where p and F representthemomentum vectorofelectronand f ield vector,respectively.Thewavefunction in the coordinate space can be obtained by Fourier transforming thewavefunction in themomentum space,which is

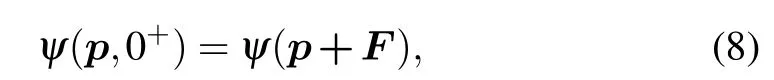
whereψ0(r)is the initial wavefunction in the coordinate space.Then,the transition amplitude can bew ritten as[40]

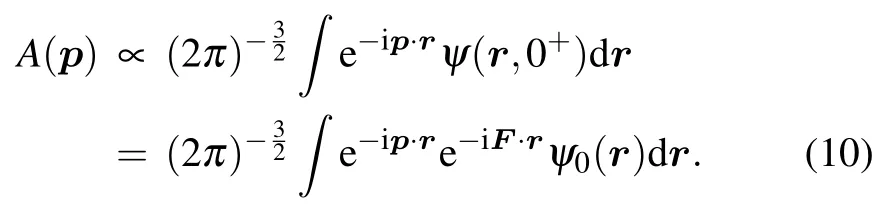
Thewave function of the 1s atomic orbital of H+2isψ1sσg=ψ1s(r-R/2)+ψ1s(r+R/2),which is the linear combinationsof hydrogenic 1sorbital located at±R/2.By taking attosecond perturbation ionization theory into account,the transition amplitude can thusbe rew ritten as

Here,|c(x)|2and|c(y)|2are the ionization probabilities along the x and y directions,respectively.Note that in the current calculations,the pulse f ield F can be ignored since the ponderomotive energies Up≪Ipand F≪p in chosen intensity,which is

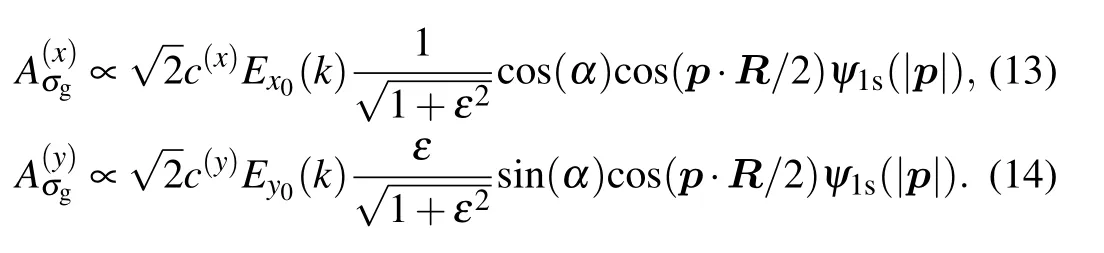
Thus,the interference term can beexpressed as

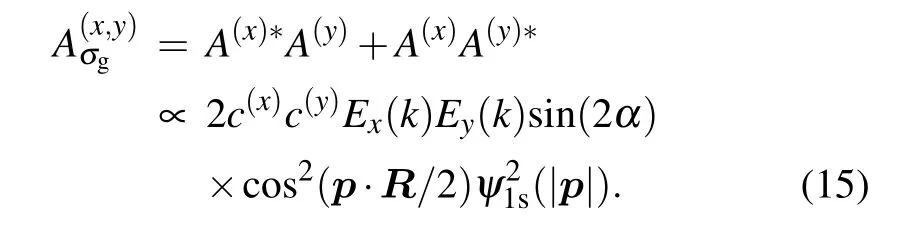
The maximum distribution meets cos2(p·R/2)=cos2(pR cosθpR/2)=1, then θpR=nπ+π/2, n=0,±1,±2,...,withθpRbeing the angle between the photoelectronmomentum p and themolecularaxis,whichmeans thatthemaximum distribution always lies in theperpendicular direction to themolecular axiswhich givesa good theoretical explanation.We have also tested the larger orientation angles up to 180°,and the tendency keeps the same as that in Fig.1.Besides,we have also considered the MPMD under different orientation angles and internuclear distances;the distribution under different conditions shows the same characteristic that is perpendicular to themolecular axis,which is not shown here.

Note that for the orientation angleθ=0°,the intensity ofMPMD underε=1.0(circularly polarized laser f ield)case(Fig.1(g))ismore intense than thatunderε=0.5(elliptically polarized laser f ield)case(Fig.1(d)).And whenθ=90°,the results reverse.

Forθ=0°,themaximum distributionmainly lies in the y direction with a small tilted angle;we focus on themodule squareof transition amplitude along the y direction

The values forε2/(1+ε2)are 0.2 and 0.5 whenε=0.5 and ε=1.0,respectively,which explains themore intense distribution in Fig.1(g)than that in Fig.1(d).

Sim ilarly,forθ=90°,themaximum distributionmainly lies in the x direction,and themodule squareof transition amplitudealong the x direction reads

Whenε=0.5 andε=1.0,1/(1+ε2)valuesare respectively 0.8 and 0.5;thus,wehavean intuitive description for themore intense distribution in Fig.1(f)than that in Fig.1(i).

Figure 2 shows the MPMD of H+2with different orientation angles under linearly polarized laser f ield(ε=0).For linearly polarized laser f ield,the transition amplitude can be w ritten as

Themaximum distribution still lies in the direction perpendicular to themolecular axis as stated above.However,for orientation angleθ=0°,theMPMD showsa distinctpattern with six lobesasdemonstrated in Fig.2(a).

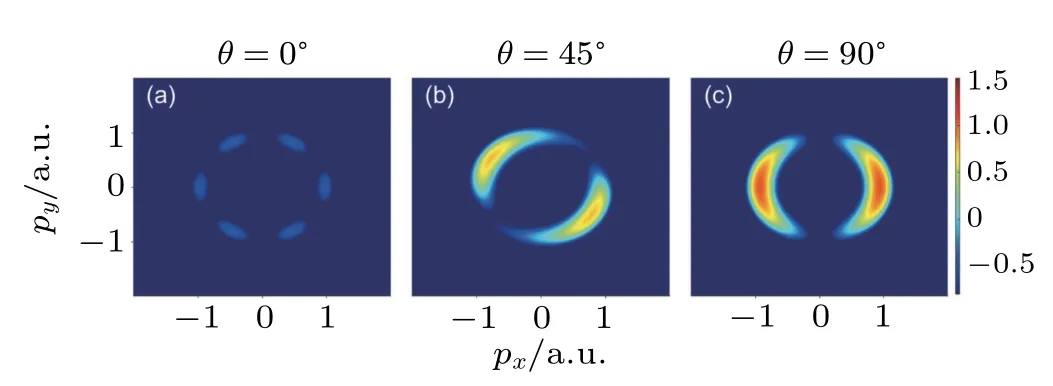
Fig.2.The 2D MPMD of H+2 under linearly polarized laser f ield with orientationangle(a)θ=0°,(b)θ=45°,and(c)θ=90°;the intensities areon a logarithmic scale.

To further understand the mechanism of the distinct MPMD of x-oriented H+2(θ=0),the evolutions of the EWP and MPMD under linearly polarized laser f ield(ε=0)and under an elliptically polarized laser f ield(ε=0.5)are shown in Figs.3 and 4,respectively.

Fig.3.The 2D EWP and MPMD of x-oriented H+2(θ=0)under linearly polarized laser f ield(ε=0)at:(a)and(d)t=2.42 o.c.;(b)and(e)t=3.63 o.c.;(c)and(f)t=4.84 o.c.Here,o.c.denotes the optical cycle;the intensitiesareon a logarithm ic scale.

Fig.4.The 2D EWP and MPMD of x-oriented H+2(θ=0)under an elliptically polarized laser f ield(ε=0.5)at:(a)and(d)t=2.42 o.c.;(b)and(e)t=3.63 o.c.;(c)and(f)t=4.84 o.c.;the intensitiesare on a logarithmic scale.

Theevolutionsof EWPin Figs.3(a)–3(c)show themovementof photoelectron under linearly polarized laser f ield(ε=0).At t=2.42 optical cycle(o.c.),theelectron isnot ionized yet,and the electron ismainly localized around themolecular nuclei;at t=3.63 o.c.,the electron has been ionized in six directions;at t=4.84 o.c.,the EWPhasevolved further in six directions.

Theevolution ofMPMDmakes theprocessof photoelectronmovementmuch clear.In Fig.3(d),theMPMD ismainly localized in the region where the initialMPMD lies because the electron isnot ionized yet.At t=3.63 o.c.(Fig.3(e)),the distribution starts to presentan interference pattern as“multiring”structure,which originates from the coherentsuperposition from EWPs ionized atdifferent timeswith the samemomentum.In Fig.3(f),the MPMD at t=4.84 o.c.presents six lobeswhich is sim ilar to the f inalMPMD andmore interference stripes,and the“multi-ring”structure becomesmuch narrower.As time evolves from t=2.42 o.c.to t=4.84 o.c.,more electrons are ionized and involved in the coherent superposition,resulting in the appearance ofmore interference stripes.

The evolutionsof EWP and MPMD under an elliptically polarized laser f ield(ε=0.5)at the same time are shown in Fig.4 for clear comparison.The EWP at t=2.42 o.c.in Fig.4(a)has the similar distribution as that in Fig.3(a)which isnotionized yet.At t=3.63 o.c.,theEWPin Fig.4(b)shows that the electron starts to ionizemainly along the y direction.In Fig.4(c),at t=4.84 o.c.,the EWPevolvesalong the y directionmuch further.

TheMPMDsat t=2.42 o.c.(Fig.4(d))and t=3.63 o.c.(Fig.4(e))under an elliptically polarized laser f ield present sim ilardistribution as thatin Figs.3(d)and 3(e)under linearly polarized laser f ield.However,the MPMD at t=4.84 o.c.presents the main distribution along the y direction which has presented the appearance of f inal MPMD as shown in Fig.1(d).Besides,theMPMD in Fig.4(f)also shows fruitful interference stripes sim ilar to that in Fig.3(f),which is due to the coherent superposition of EWP ionized at different times with the samemomentum.Thus,it can be seen from Figs.3 and 4 that the f inalMPMD can be inf luenced by theellipticity of the laser f ield.

4.Conclusions

In summary,we study the MPMD of H+2with different orientation angles in an elliptically polarized laser f ield by numerically solving the 2D TDSE under the frozen-nuclei approximation.Our numerical results show the dependence of MPMD on orientation angleand laserellipticity.Theattosecond perturbation ionization theory and the exactly solvable photoionization model are employed to explain the results.The evolutions of both EWP and MPMD withθ=0°under linearly and elliptically polarized laser pulsesare presented to interpret the distinct f inal MPMD pattern withθ=0°under linearly polarized laser pulse.