Optical solitons supported by finite waveguide lattices with diffusive nonlocal nonlinearity∗

Changming Huang(黄长明) Hanying Deng(邓寒英) Liangwei Dong(董亮伟) Ce Shang(尚策)

Bo Zhao(赵波)1, Qiangbo Suo(索强波)1, and Xiaofang Zhou(周小芳)1

1Department of Electronic Information and Physics,Changzhi University,Changzhi 046011,China

2School of Photoelectric Engineering,Guangdong Polytechnic Normal University,Guangzhou 510665,China

3Department of Physics,Shaanxi University of Science&Technology,Xi’an 710021,China

4King Abdullah University of Science and Technology(KAUST),Physical Science and Engineering Division(PSE),Thuwal 23955-6900,Saudi Arabia

Keywords: optical solitons,diffusive nonlocal nonlinearity,linear stability analysis

1. Introduction

Spatial localization of light beams in optical structures has attracted considerable attention during the last two decades. Multiple studies have been devoted to the existence and stability of nonlinear waves in different nonlinear media.[1–8]Nonlocal nonlinear media,including thermal nonlinear media,[9–12]liquid crystals,[13–15]and photorefractive crystals[16,17]can also be used for trapping optical beams.

An important branch of this topic is to study the effect of asymmetric nonlocal diffusion nonlinearity on the formation and stability of optical solitons. In homogeneous optical structures, the propagation dynamics of cnoidal waves[18]and coupled soliton pairs[19]have been studied. Localized surface waves and their specific features at the interface between the linear dielectric and photorefractive medium with drift and diffusion nonlinearity have been studied.[20,21]The oscillatory behavior of spatial solitons in a gradient refractive index waveguide with nonlocal nonlinearity has been reported.[22]In periodic or semi-infinite periodic optical lattices, soliton self-bending,[3]gap solitons,[23]surface lattice solitons,[24–26]spectral tunneling of walking spatial solitons,[27]fundamental defect mode,[28]fundamental and higher-order solitons,[29]controllable soliton propagation,[30]and solitary wave formation[31]have been addressed. In addition,a mechanism for stable spatial soliton formation based on the competition between strongly asymmetric nonlocal nonlinearity and spatially localized gain superimposed on a wide pedestal with linear losses has been presented.[32]The photorefractive media and physical parameters relating to optical solitons have been reported.[24,26,27,32,33]To summarize, the stable asymmetric solitons are an active research topic. However,to the best of our knowledge,the nonlinear dynamics of optical solitons in finite waveguide lattices with diffusive nonlocal nonlinearity has never been explored.

In this article,we study the existence and stability of optical solitons in three types of finite waveguide lattices with asymmetrical nonlocal nonlinearity. It is relevant to stress that our model is substantially different from those obtained in periodic[23]and semi-infinite[24]optical lattice, where gap solitons with oscillating decaying tails inside the multiple lattice channels were investigated. In contrast to solitons reported in Refs. [23,24], we find that fundamental and multipeaked solitons are power thresholdless. Two opposite soliton self-bending signals do not affect the existence and stability of these solitons due to the symmetrical distribution of the waveguide lattices. Moreover, we also study in detail the properties of two-peaked and three-peaked twisted solitons supported by their corresponding characteristic waveguide lattices.

2. Mathematical model

We consider light propagation along thezaxis in an unbiased photorefractive crystal with finite waveguide lattices and intrinsic diffusion nonlinearity. The dynamics of the beam can be described by the nonlinear Schr¨odinger equation for the dimensionless amplitude of the light fieldψ(x,z)[24]

where the transversexand longitudinalzcoordinates are scaled to the beam widthx0and diffraction lengthk0x20,respectively, andk0=2π/λ0.ψ=k0n0(x0KBTre/2eId)1/2Ais the field amplitude of the light beam,wheren0is the refractive index,KBis Boltzmann constant,Tis the absolute temperature,reis the electro-optic coefficient,eis the electron charge,andIdis the dark irradiance of the crystal.S=2e/k20x0n20KBTreis the saturation parameter.gxdescribes the magnitude of the nonlocal diffusion component of the nonlinear response.Whengx=+1,light beam tends to self-bend towardx →+∞,while whengx=−1, light beam tends to self-bend towardx →−∞. The functionV(x) (V(x) =p[1+cos(Ωx)] forx1≤x ≤x2, andV(x)≡0 otherwise)describes the profile of the finite waveguide lattices,where the parameterspandΩare the lattice depth and lattice frequency,respectively. Following the dimensionless coordinates and variables,we know thatx0is an arbitrary spatial width and the beam power density has been scaled with respect to the dark irradiance of the crystalId,and Eq.(1)can be derived from the Kukhtarev model.[34,35]

The stationary soliton solutions that can be supported by Eq. (1) are of the formψ(x,z)=w(x)exp(iβz), wherew(x)is a real function describing the amplitude profiles andβis the real propagation constant of solitons. After substituting the solution into Eq. (1), we arrive at a system of differential equations for the soliton amplitude as follows:

To elucidate the stability properties of solitons, following the standard procedure, we search for perturbed solutions of Eq. (1) in the form ofψ(x,z) = [w(x)+u(x,z)+iv(x,z)]exp(iβz), where the perturbation componentsuandvcan grow upon the propagation with a complex growth rateλ=λr+iλi. Inserting this expression into Eq.(1)and dropping the higher-order terms inuandv, a linear eigenvalue problem can be obtained as follows:

3. Numerical results and discussion

Firstly,we address the properties of fundamental solitons supported by an isolated waveguide lattice, that is, N = 1,x1=−π/2, andx2=+π/2. Typical profiles of asymmetric fundamental solitons are shown in Fig.1(a). We find that with a decrease in the propagation constant, the amplitude of the soliton increases gradually. The curves of soliton powerU(β)are indicated in Fig. 1(b). In this study, two different lattice depths are considered, that is,p=1.5 andp=3.0. Obviously, the existence region of solitons depends on the lattice depth (considering that forβ →0, the soliton power is extremely large and the soliton is unstable. Here,we only show the results ofU<100). With an increase inp, the existence domain of the soliton gradually widens[also see Figs.1(c)and 1(d)]. Importantly,we find that the fundamental soliton has no threshold power in such an isolated waveguide lattice, which is in sharp contrast with the results in Ref. [24], where the surface lattice soliton could only be found above a threshold power.

Fig.1.(a)Profiles of solitons at β =2.1(blue line)and β =4.0(red line).(b)Power U,(c)central coordinate xc,and(d)effective width weff versus propagation constant β for p=3.0 and p=1.5 at gx=1.In(b)–(d),the black,red,and cyan segments represent stable, weakly unstable, and unstable solution branches,respectively.

The profile distribution of fundamental solitons is closely related to the nonlocal nonlinearity of materials. We found that,with an increase in the soliton power,the off-center position[Fig.1(c)]and the effective width[Fig.1(d)]of the soliton gradually increases. It should be pointed out that the position corresponding to the half width of a single waveguide lattice is±π/4, and when the power of the solitons isU6.17 forp=1.5 andU15.66 forp=3.0, the central coordinate isxc>π/4. In other words, with a further increase in power,most of the profile of fundamental solitons is distributed outside the waveguide lattice and only a small part is confined in the single waveguide lattice. This characteristic indicates that solitons are unstable when the soliton power exceeds a certain value.

The stability of fundamental solitons is one of the important problems. We performed a comprehensive linear stability analysis by solving Eqs.(3)and(4). The results show that: (i)Fundamental solitons in the region near the upper cutoff values are completely stable,and the solitons in the middle region oscillate weakly and are unstable. In these two cases,the power of the fundamental solitons is small or moderate. When the power of the solitons exceeds a certain value,the soliton propagates for a short distance and collapses rapidly. (ii)The stability characteristics of the fundamental solitons can be qualitatively explained by the properties of the central coordinate and the effective width of solitons.When the center coordinate of the soliton’s profile deviates far from the center coordinate of the waveguide lattice (the effective width is large, or the power is large), the fundamental soliton is unstable. (iii)The larger the lattice depth, the wider the corresponding regions of stable existence, such asβ ∈[1.4,1.9189] atp=1.5 andβ ∈[2.92,4.052]atp=3.0.

Fig. 2. Profiles of (a) two-peaked (b) and three-peaked solitons at β =3.5.V is enhanced by 0.5 to distinguish from w. (c) Power U of the fundamental,two-peaked,and three-peaked solitons in different waveguide lattices.(d)Rear part of the perturbation growth rate λr for fundamental,two-peaked,and three-peaked solitons. In all cases,gx=+1 and p=3.0.

In addition, two-peaked and three-peaked solitons are also considered in their corresponding characteristic waveguide lattices [Figs. 2(a) and 2(b)]. The peaks of multi-peak solitons with the same phase are localized in each waveguide,which can be regarded as a combination of two or three fundamental solitons. Moreover, the fundamental, two-peaked,and three-peaked solitons share the same upper cutoff value at a fixed lattice depth [Fig. 2(c)]. Linear stability analysis reveals that with the increase in the peak number of multi-peak solitons, the stable region of the solitons gradually shrinks[Fig.2(d)].

Fig. 3. (a) The power U versus propagation constant β for gx =1 (black line) and gx =−1 (purple line). (b) Enlarged view near the upper cutoff value in(a). (c)The central coordinate xc of the out-of-phase solitons versus β for two different gx. (d) Profiles of two soliton solutions for gx =1 and gx =−1 at β =4.39. To distinguish from w,V is enhanced by 0.1. (e)–(f)Real part of perturbation growth rate λr versus different propagation constant β at gx=+1. In all cases, p=3.0.

We further study the properties of the two-peaked twisted solitons supported by double waveguide lattices with two opposite nonlocal signs ofgx. In such a lattice, N =2,x1=−π/2, andx2=+3π/2, and we mainly study the existence of optical solitons featuring the main peak in the left waveguide lattice. Whengx>0, the central coordinatexcof the asymmetric soliton profile should be greater than 0. Whengx<0,xcshould fall in the regionx<0. Due to the characteristics of two opposite nonlocal nonlinear signals and the asymmetric distribution of the waveguide lattice atx=0,notably differences exist in the soliton-existence regions for both cases[Fig.3(a)]. Whengx=−1,similar to that of the single waveguide lattice, the two-peaked twisted soliton family has no power threshold, whereas whengx=+1, the soliton family has a power threshold and is constrained to a narrow power range[Figs.3(a)and 3(b)]. Forgx=+1,we should point out that (i) when the power of the soliton increases, this asymmetrical nonlocal nonlinear term of Eq.(1)also increase. The main peak of the soliton localized in the left waveguide lattice is dragged into the right waveguide lattice. This new soliton family is not considered in our paper. (ii)Whenβapproaches the upper cutoff value, the power of the soliton is small, and the reflection of the right waveguide lattice counteracts the diffusion of the light beam.

Compared withgx=+1, the off-center position of the solitons forgx=−1 is far away from the right waveguide lattice [Fig. 3(c)]. Asymmetrical nonlocal nonlinearity leads to unequal peak amplitudes of the two-peaked twisted soliton families supported by double waveguide lattices localized in two lattice channels. As seen in Fig. 3, the soliton family withgx=−1 is less affected by the right waveguide lattice than the soliton family withgx=+1. The soliton localization inside the right waveguide lattice is shallower than that forgx=+1 [Fig. 3(d)]. Forgx=−1, the stability of twopeaked twisted solitons is similar to the piecewise distribution of fundamental solitons in a single waveguide lattice. Forgx=+1, stable two-peaked twisted solitons exist in a large middle region of their existence domain. Whenβapproaches the upper cutoff value(in an extremely narrow region, where dU/dβ>0), two-peaked twisted solitons exhibit exponential instability. Whenβis near the lower cutoff region, the two-peaked twisted soliton is characterized by weak oscillation instability,whereλr≪λi. The instability growth rates of out-of-phase solitons forgx=+1 are plotted in Figs.3(e)and 3(f),respectively.

We also study the existence and stability of twisted solitons supported by three waveguide lattices. Here, the fixed parameters in such a lattice are N = 3,x1=−3π/2, andx2=+3π/2.When the main peak of the soliton is localized in the leftmost lattice channel, the existence region and the stability of the soliton for both signs ofgxare similar to the characteristics of a soliton in a double-waveguide lattice. A new soliton family(named three-peaked twisted solitons)has been explored. That is, the main peak of which is localized in the middle waveguide lattice channel. Owing to the symmetrical distribution of the three waveguide lattices,the opposite signs ofgxonly change the self-bending direction of three-peaked twisted solitons but do not affect the existence and stability of solitons. We only discuss the case ofgx=+1.

Representative profiles of three-peaked twisted solitons are shown in Figs.4(a)–4(c). The twisted solitons with moderate power levels have different amplitude peaks in the three lattice channels [Fig. 4(a)]. When the propagation constant of the three-peaked twisted soliton approaches the lower cutoff value,the amplitude difference in the left and right lattice channels is more prominent in the deeper lattice [Figs. 4(b)and 4(c)].In contrast to the power curve of two-peaked twisted solitons supported by double waveguide lattices forgx=+1,the power curve of three-peaked twisted solitons is characterized as a non-threshold at a large lattice depth [Fig. 4(d)].Comparing the lattice depthp=1.5 andp=3.0,the existence domain of the three-peaked twisted soliton gradually increases with the increase in lattice depth. For these two cases, the effective width of the three-peaked twisted soliton decreases with the decrease in the propagation constant, except for a narrow region near the upper cutoff[Fig.4(e)]. Linear stability analysis reveals that a very narrow unstable domain exists(1.8414≤β ≤1.8439)near the upper cutoff region atp=1.5,while the unstable domain(2.87≤β<3.15)atp=3.0 is near the lower cutoff region[Fig.4(f)].

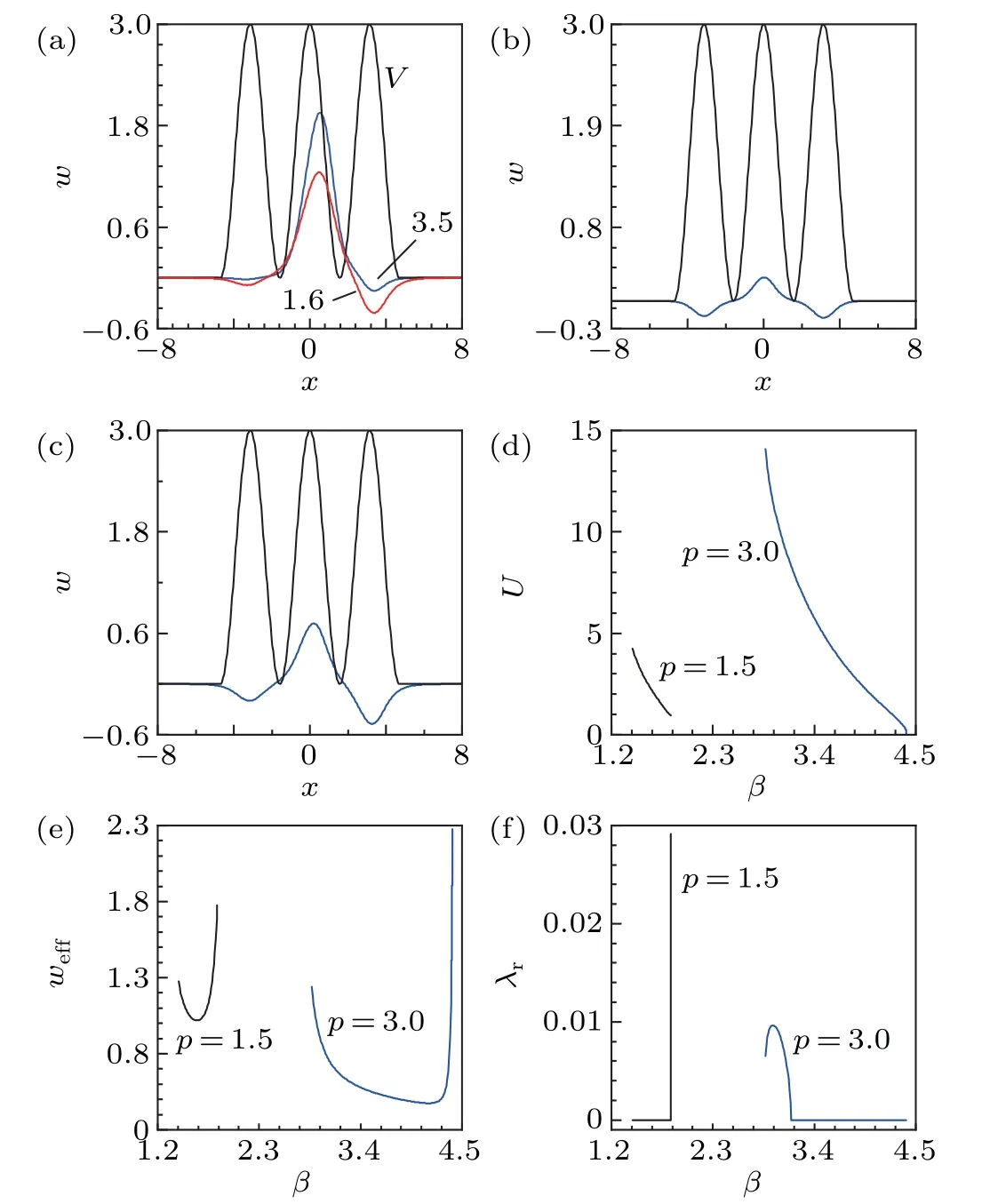
Fig.4. Profiles of three-peaked twisted solitons at(a)β =3.5, p=3.0,and β =1.6, p=1.5,(b)β =4.396, p=3.0,and(c)β =1.843, p=1.5. V in(a)–(c)is enhanced by 0.5 to distinguish from w. (d)Power U,(e)effective width weff,and(f)real part of perturbation growth rate λr versus propagation constant β for two different lattice depths p. In all cases,gx=+1.

To further verify the stability of the optical solitons supported by three types of waveguide lattices, we simulated the evolution of the stationary solutions in the framework of Eq. (1) by using the standard fourth-order Runge–Kutta integration scheme. The input conditions areq(x,z= 0) =w(x)[1+ερ(x)],whereρ(x)describes a random function with values ranging from−1 to +1. We setε= 0.05 in our simulation. Typical stable examples of fundamental, twopeaked twisted, and three-peaked twisted solitons are shown in Figs. 5(a), 5(d), and 5(g). All the real parts ofλfor these solitons are equal to zero. We can find that the profiles|w|of these solitons are maintained during propagation. The fundamental solitons with moderate power and the two-peaked twisted solitons near the lower cutoff region are characterized by a weakly oscillating unstable propagation [Figs. 5(b) and 5(e)]. It can also be seen in detail that the moduli of their field distributions fluctuate with the propagation distancez.The typical linear-stability spectrum of the linearization operator for a two-peaked twisted soliton atp=3.0 andβ=3.0 is plotted in Fig. 5(f). When the fundamental soliton has a higher power, the shape of the soliton collapses rapidly owing to its large off-center position and diffusive nonlinearity[Fig.5(c)]. When the propagation constantsβare very close to the upper cutoff region (where dU/dβ>0, see theU(β)curves of the two-peaked twisted solitons in the double waveguide lattices withp=3.0 and three-peaked twisted solitons in the three waveguide lattices withp=1.5), the peak value of the soliton increases rapidly with increasing propagation distance [Fig. 5(h)]. An example of the linear-stability spectra of solitons localized in this narrow region is depicted in Fig.5(i)]. Therefore,the results of the linear stability analysis and the propagation evolutions of the above optical solitons are in good agreement. In addition,we mention that the nonlocal contribution to the nonlinear response also results in self-bent light beam propagation in such finite waveguide lattices (see Refs.[3,23,24,36]for similar phenomena).

Fig. 5. Stable (a), (d), (g), unstable (b), (h), and weakly oscillating unstable (c), (e) propagation examples of solitons. (a) β =3.8, (b) β =0.7,(c)β =2.1, (d)β =3.7, (e)β =3.0, (g)β =1.6, and(h)β =1.843. N=1 in(a)–(c), N=2 in(d)–(f), and N=3 in(g)–(i). The initial state was perturbed by adding 5% amplitude initial perturbations. The linear stability spectra of (f) a two-peaked twisted soliton at β =3.0 and (i) a three-peaked twisted soliton at β =1.843. p=3.0 in(a)–(f),and p=1.5 in(g)–(i). In all cases,gx=+1.

4. Conclusion

In conclusion,we have reported that three families of optical solitons can exist in finite waveguide lattices imprinted in photorefractive media with asymmetrical diffusion nonlinearity. The properties of fundamental, multi-peaked, and multipeaked twisted solitons in their corresponding characteristic waveguide lattices have been discussed. We found that power thresholdless asymmetric fundamental solitons can exist in an isolated waveguide lattice. With an increase in its power, the degree of asymmetry and the effective width of the fundamental solitons gradually increase. Fundamental and multi-peak solitons share the same upper cutoff value at a fixed lattice depth. In addition, we found that the fundamental and multipeaked solitons are completely stable only near the upper cutoff region. With an increase in the peak number of multi-peak solitons,the stable region of the solitons gradually shrinks. A two-peaked twisted soliton is characterized by its main peak localized in the left waveguide lattice. When solitons tend to self-bend toward the right waveguide lattice, stable twopeaked twisted solitons exist in a larger region in the middle of their existence domain, and weakly oscillating and exponentially unstable solitons can be found near the lower and upper cutoff regions. The existence of the power threshold for the three-peaked twisted soliton depends on the depth of the waveguide lattice. Linear stability analysis corroborated by direct evolution simulations revealed that the stability region of three-peaked twisted solitons is in the lower(upper)cutoff region for a shallow(deep)lattice depth.