Elastic electron scattering with formamide-(H2O)n complexes(n=1,2): Influence of microsolvation on the π∗and σ∗resonances∗

Kedong Wang(王克栋), Yan Wang(王言), Jie Liu(刘洁),Yiwen Wang(王怡文), and Haoxing Zhang(张浩兴)

School of Physics,Henan Normal University,Xinxiang 453007,China

Keywords: electron scattering,elastic cross section,hydrogen-bonding,shape resonance

1. Introduction

Low-energy electrons (LEEs), formed in secondary processes that accompany high-energy light-matter interactions,are the key players in radiation damage of biomolecules, including DNA[1]and proteins.[2]These electrons can be temporarily trapped to form transient negative ion(TNI)species,which further undergo electronic and structural transformation leading to fragmentation, a process called dissociative electron attachment (DEA). LEE-induced damage to DNA was first experimentally demonstrated by Sanche and co-workers who showed that LEE irradiation results in single-and doublestrand breaks in DNA.[3]Since then, many experimental and theoretical works[1,4–9]have been devoted to the LEE-induced fragmentation of biomolecules to obtain a comprehensive picture of the damage mechanism. In the DEA process, bothπ∗[10]andσ∗[11]shape resonances play an important role. It is worth noting that any effect that can change the position in energy and the lifetime of these resonances may also affect all the processes related to those states,as DEA.

Many electron scattering experiments and calculations consider biologically relevant molecules in the gas phase and the influence of the environment is neglected in the collision.However, biological radiation damage occurs in a condensed environment where all molecules with a biological function are surround by other molecules,mainly water.Clusters can be proposed as systems that bridge the complexity gap between the gas phase and condensed phase.

From an experimental point of view, there are a series of the DEA measurements in molecular clusters.[12–16]The experimental study on microhydrated biomolecules including pyrimidine[12]and uracil/thymine[13]show quenching of some of the DEA channels, but this is ascribed by the authors to nuclei-related caging effects rather than changes to resonance spectrum and characteristics. EA mass spectra for uracil, 5-fluorouracil, and 5-bromouracil with different degrees of hydration were reported[14]and energy transfer between these three molecules and the solvent was investigated. Koˇciˇseket al.[15]reported experimental fragmentation patterns for DEA to microhydrated 2-deoxycytidine 5-monophosphate. They observed glycosidic C–N and sugar-phosphate P–O bond dissociations as the primary and secondary fragmentation channels, respectively. A recent experiment for nimorazole made by Meißneret al.[16]demonstrated that DEA represents only a minor reaction channel which is further suppressed upon hydration.

Theoretically, the cross sections for dehydrogenation from uracil/thymine have been calculated.[17]Subsequently,the results of this work were presented by Sieradzkaet al.[18,19]They investigated the effect of microsolvation on theπ∗shape resonances of pyridine and thymine using theR-matrix method and discussed the additive effect of water molecules hydrogen-bonding to isolate molecules. Bettega and co-workers investigated CH2O–H2O[20]and singly and doubly hydrated formic acid[21]and phenol[22]using the Schwinger multichannel method. They showed thatπ∗shape resonances can be either stabilized or destabilized,depending on the role played by water molecules in the H-bonds. Recently, Fabrikant[23]reviewed the suppression and enhancement effects in DEA in a cluster environment.

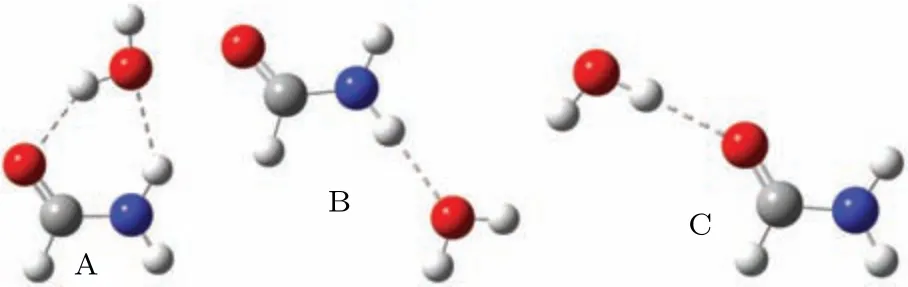
Fig.1. Three structures of formamide–H2O complexes named as A to C.

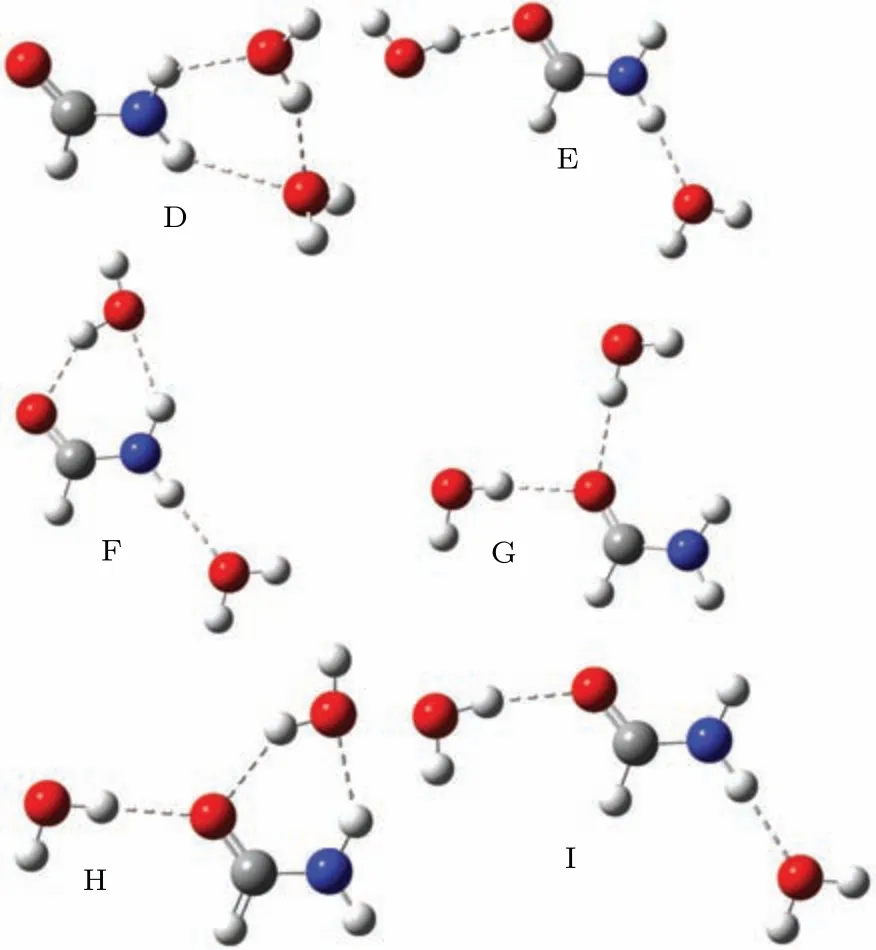
Fig.2. Six structures of formamide-(H2O)2 complexes named as D to I.

In this paper we extend the investigation to a single formamide and water complex. Formamide, HCONH2, is the smallest molecule that contains the peptide linkage. Resonant spectra[24–26]for the isolated formamide have been reported with the experimental methodologies, and theoretical calculations including the molecular complex optical potential approach,[26]single-center expansion,[27]Schwinger multichannel method,[28]andR-matrix method.[29]The results show that there is aπ∗shape resonance in the energy region from 2.1 eV to 3.8 eV, and aσ∗resonance at around 15 eV. This system involves an indirect DEA process, where the electron is captured into theπ∗resonance, which crosses theσ∗anion potential curve,leading to the C–N bond breakage. To investigate the influence of microsolvation in theπ∗andσ∗resonances of formamide, we consider one and two surrounding water molecules. We discuss what causes the stabilization or destabilization of theπ∗andσ∗resonances of solutes in terms of the net charge in the solute. The elastic scattering calculations reported here are carried out with the UK molecularR-matrix code.[30,31]The cross sections are obtained in the static-exchange (SE) approximation for energies ranging from 0.01 to 8 eV. We also perform additional electronic structure calculations to interpret our results. The calculations are performed at the equilibrium geometry. The initial geometries of the cluster are extracted from a liquid phase model which has been described in Ref.[32]. According to their results, the formamide molecule bound with the water molecules together by hydrogen bonds in the sites of O and H of the amino-group. Considering that the isolated formamide molecule belongs toCspoint group,we subsequently reoptimized the clusters in the same point group at B3LYP/6-311++G∗∗level. Three structures obtained in this work are shown in Fig.1.for formamide–H2O complexes,labeled from A to C, and six formamide-(H2O)2structures are shown in Fig.2,labeled from D to I.

2. Theoretical method

TheR-matrix method has been described in detail elsewhere[33]and here we only outline its key features. The method is based on the division of space into an internal region containing all theN-electron target charge cloud and an external scattering region. In the inner region the discretized continuum(N+1)-electron wave function is written using the CI expression

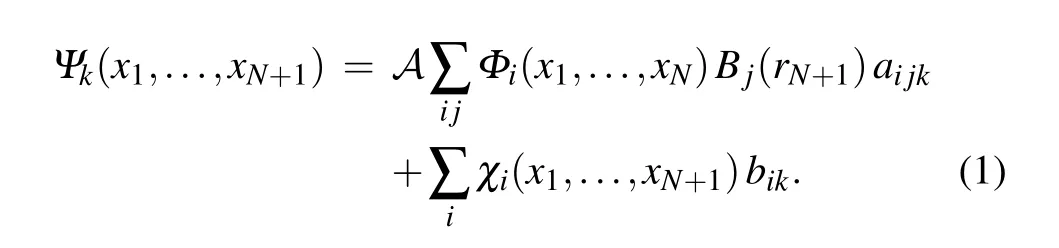
Here theΦidenotes the channel functions constructed from theN-electron target states, andAis an antisymmetrization operator,whilexNis the spatial and spin coordinate of theNth electron,represents theith state of theN-electron target,Bj(r)represent the continuum orbitals. Coefficientsaijkandbikare variational parameters determined as a result of the matrix diagonalization. The second summation in Eq. (1) involvesL2configurations where all electrons are placed in orbitals associated with the target. Such configurations are essential in even the simplest model which does not include any target relaxation, the SE approximation, to allow for orthogonalization between the continuum orbitals and those belonging to the target. In the more sophisticated modelsL2configurations are also essential for introducing the effects of target polarization.Given that both shape and Feshbach resonances are localized in the region of the target then it is clear that the resonance parameters will also be sensitive to these configurations which are included in the calculation.

In the outer region, a long-range multipole expansion is used to represent the electron-target interaction. TheR-matrix is built at the boundary between the inner and outer regions,using the inner region information, and the one particle multichannel problem is solved by propagating theR-matrix outwards up to a radius (here is 100a0) large enough so that an asymptotic expansion for the radial wave functions can be matched to known analytical solutions. In such a way,the Kmatrix and S-matrix and thus resonance parameters and cross sections can be determined.

Scattering calculations were carried out in the SE approximations. In the former,only one target wavefunction(for the ground state of the molecule),represented at the Hartree–Fock(HF)level,is included in expansion(1). TheL2functions take a simple form in the following way:

Since it is not possible to quantify how much polarization theL2functions describe,there is no simple way to determine the optimal number of virtual orbitals(VOs).

The HF self-consistent field(SCF)wave function with the cc-pVDZ basis set is used in the scattering calculation. Our calculated ground-state energy and dipole moment of the clusters and isolated formamide are collected in Table 1. The dipole moment of 1.57 a.u. was obtained for formamide,which is in good agreement with the available experimental value 1.46 a.u.[34]No experimental values of the dipole moment for these clusters are available. For the scattering calculation,R-matrix radius is taken as 15a0,wherea0is the Bohr radius,and continuum orbitals up togpartial wave(l=4)are represented by Gaussians centered at the molecule center of gravity.[35]

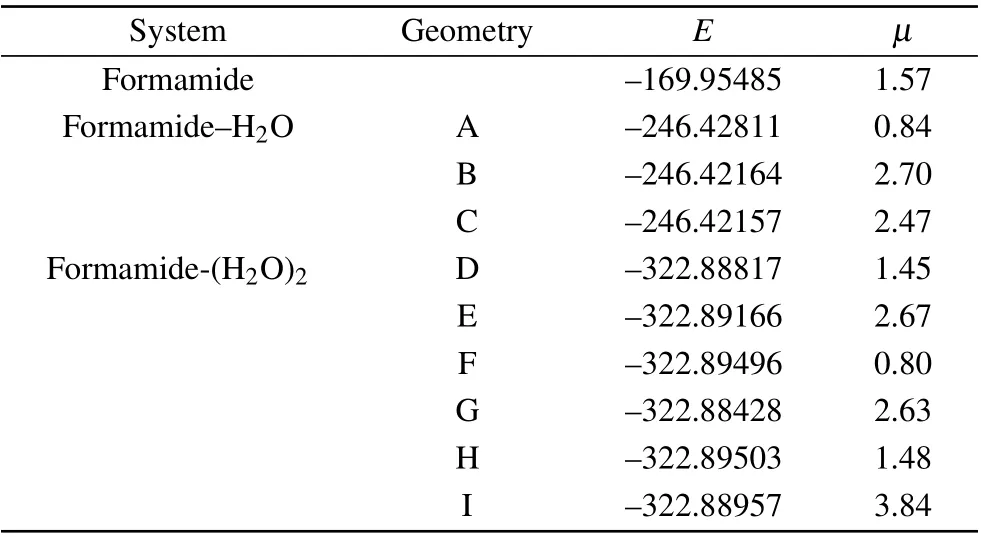
Table 1. Ground state energies (E)in Hartree and dipole moment(µ)in a.u. for formamide and formamide–(H2O)n complexes(n=1,2).

We have also calculated the elastic integral cross section(ECS)for the isolated formamide. In order to check the convergence,we tested the result with three different calculations including 20, 30 and 40 VOs for the formamide molecule in the SE approximation. All these three results predictπ∗anion states located at the same position about 4.64 eV with a very similar width of 1.78 eV, which is in agreement with the previous study[28,29]in the SE approximation. The result with 40 VOs predicts twoσ∗resonances in the energy region between 15.0 and 20.0 eV,and noσ∗resonance is detected in the result with 20 VOs. Oneσ∗resonance is detected in the 30 VOs result, which agrees with the available SEP results[26,27]that there is aσ∗resonance located at about 15.0 eV. Then we choose a total of 30 VOs included in the SE calculation for all systems. Such a result illustrates that,as the energy of the scattering electron increases,modeling of the correlation between it and the molecule becomes more difficult. Hence we present the scattering results in the energy region of 0.01–8 eV and do not study the high-lyingσ∗resonance in the scattering results.

Fig. 3. Elastic integral cross section for electron scattering from formamide,formamide–H2O complex A,and formamide-(H2O)2 complex I with different partial waves l ≤4 and l ≤6 at the SE approximation.

All the complexes considered here have a permanent electric dipole moment.The long range character of the dipole potential requires the use of the standard Born closure to include higher partial wavel>4 and to improve the cross sections.However,this potential only affects the background scattering and does not change the location of the resonances. Since our main interest here is the description of shape resonances of the complexes, we choose to present only the ECSs without including the Born correction. However,the contributions from the high partial wave could become important with increasing the size of the cluster. Thus,we compare the results using partial wavesl ≤4 andl ≤6 for the isolated formamide,one formamide–H2O complex (here is A), and one formamide–(H2O)2complex (here is I). The UKRmol+suite[36]is used to perform the scattering calculations with the partial wavesl ≤6. The calculated ECSs are shown in Fig. 3. As is expected, the inclusion of the more dipole potential in the calculations increases the cross sections. However, this has no effect on the position of resonances as shown in Fig. 3, and then partial wavesl ≤4 are used to describe the potential in the presentR-matrix method.

3. Results and discussion

Figure 4 presents the ECSs andA′′symmetry decomposition for the isolated formamide and three formamide–H2O complexes A to C in the SE approximation, where the signatures of theπ∗resonance are clear in all systems. As shown in Fig. 1, the water molecule plays the role of proton acceptor for complex B, while it acts as proton donor for complex C. The calculated resonant position for complex B is located at 5.34 eV,with a 0.70 eV above the resonance of the isolated formamide molecule.However,for complex C the peak moves to a lower energy in comparison to theπ∗resonance of formamide, located at 4.21 eV. This corresponds to a downshift of 0.62 eV in comparison with the SE result of the isolated formamide molecule. A slight downshift 0.16 eV is found for complex A. In this complex, there are two hydrogen bondings: the water not only acts as a proton donor(OH···O=C)but also as the proton acceptor (O···HO). The length of hydrogen bonding in the former (1.917 ˚A) is shorter than that in the latter(2.053 ˚A).Therefore,such a result illustrates that water behaves more strongly as a proton donor than a proton acceptor for complex A.This explains the stabilization of theπ∗resonance. These results show that water acting as proton donor stabilizes the resonance. However,when it acts the proton acceptor, the resonance destabilizes and shifts to higher energy. The results confirm the conclusions obtained by Freitas,Bettga and collaborators[20–22]using the Schwinger multichannel method and by Sieradzka and Gorfinkiel[18,19]using theR-matrix method.

The SE approximation usually gives the shape resonances of the higher energy since it does not include attractive target polarization effects. Nonetheless it is the most appropriate to investigate changes to the resonances due to hydration with theR-matrix approach.The SEP approximation cannot be performed in a converged manner, although it includes polarization effects. Since it is not possible to quantify how much polarization is being described by a specific calculation, we are unable to ensure that the same amount of polarization is included in different calculations. If the experimental data are available, usually one use experimental positions of the low-lying resonances as the way to determine the best set ofL2configurations.[18]Since no prior data are available for the resonances of microhydrated formamide or similar targets,we are unable to adopt this approach in this case. Then it is not possible to confidently obtain quantitative energy shifts from a comparison of the resonance positions from the SEP calculation.

Fig.4. Elastic integral cross section and the A′′ symmetry decomposition for electron scattering from formamide and formamide–H2O complexes at the SE approximation.

In Fig. 5 we show the ICSs of six formamide–(H2O)2complexes D to I in the SE approximation, in comparison with the isolated formamide molecule.The contributions from theA′′symmetry to the ICSs of formamide and formamide–(H2O)2complexes are also shown in the picture. There is one structure at around 5.62 eV in the ICS for complex D. This resonant peak shows a shift of 0.98 eV to higher energy compared to the SE result of the formamide molecule. The same behavior is seen for complex F, in which theπ∗shape resonance at around 5.03 eV and 0.39 eV higher than the isolated formamide molecule. The slight shifts to higher energy of 0.10 eV and 0.20 eV are found for complex I and complex E, respectively. However, for complexes G and H, the peaks lie at 3.21 eV and 3.77 eV, and correspond to a down shift of 1.43 eV and 0.87 eV, respectively. As shown in Fig. 2, in complex D both water molecules act as the proton acceptor,

where for G, they act as the proton donor. We observed the expected behavior in the resonances:destabilization for D and stabilization for G.Let us look at the structures for complexes F, H, and I in the picture. It is found that F corresponds to A plus B,H corresponds to A plus C,and I corresponds to B plus C.For theπ∗shape resonances in complexes F,H and I,we found that the effect of water on the formamide resonance is approximately additive,theπ∗resonances for complexes F and I are destabilized,and for the complex H is stabilized.The similar additive effect of water molecules hydrogen-bonding to thymine was discussed by Sieradzka and Gorfinkiel.[19]

Fig. 5. Elastic integral cross section and the A′′ symmetry decomposition for electron scattering from formamide and formamide–(H2O)2 complexes at the SE approximation.

As mentioned above, the positions ofπ∗resonances for three formamide–H2O complexes vary from 4.21 eV to 5.34 eV and for six formamide–(H2O)2complexes vary from 3.21 eV to 5.62 eV at the SE approximation. The maximum differences among them are 1.13 eV for formamide–H2O complexes and 2.41 eV for formamide–(H2O)2complexes. This means that conformation plays an important role in the determination of the resonances. This result is in agreement with the findings reported recently by da Mata and coworkers[37]for the case of formaldehyde dimers through the use of molecular complex optical potential(MCOP)approach.Sieradzka and Gorfinkiel[18]discussed the indirect effect on the resonance positions. This effect is due to the changes to molecular geometry resulting from binding with water. It should be noted that our results here equated to the total effect in their results.[18]

Both position and width are important parameters for a resonance. The microhydration environment leads to the shift in the position of theπ∗anion state through the H-bonding,and it may also affect the width of the anion state. Here we fit the resulting eigenphase sums to a Breit–Wigner profile[38]to obtain the position and width of the resonance. Except for the position of the obtained resonances discussed above,their widths are also listed in Table 2. For formamide–H2O complexes,we obtained the widths 1.44 eV,1.98 eV and 1.51 eV for A, B and C, respectively. When compared to the isolated formamide molecule, the calculated widths ofπ∗resonance are reduced by 0.34 eV for A and 0.27 eV for C, increased by 0.20 eV for B.For formamide–(H2O)2complexes,the surround water lowers the widths ofπ∗resonances to 0.15 eV(for E),0.19 eV(for F),0.80 eV(for G),0.73 eV(for H),and 0.15 eV(for I).Theπ∗resonance for D shows almost the same width as the isolated formamide molecule. Our results show the surround water molecules have a substantial influence on the width ofπ∗resonance. The width of the resonance is related to the lifetime of the anion state and plays a key role in the DEA process. The narrower the width is, the higher the survival probability of the anion state is, and the larger DEA cross sections are. Our results indicate that the process of electron-induced bond breaking in the formamide molecule can be strongly influenced by surround water molecules and are worthy of further investigation.

To interpret what causes the stabilization/destabilization of the resonance of the solute in the complexes, we have carried out additional bound state calculations. The results including the scaled virtual orbital energy (SVOE) and the net charge in the solute are presented in Table 2. First, we optimized the geometry at the second-order Møller–Plesset perturbation theory(MP2)using the 6-31G(d)basis set,and used this geometry and the same basis set to compute the molecular orbitals and their energies at the HF level. We are interested in the lowest unoccupieda′′molecule orbital for the isolated formamide and complexes A to I. These lowest unoccupieda′′molecule orbitals are most concentrated along the C=O bond, and are responsible for theπ∗shape resonances. The plots of these orbitals for formamide, A and D are shown in Fig. 6. LUMO+5 for formamide is aσ∗(a′)molecule orbital and has the same shape as the resonantσ∗orbital shown by Goumanset al.[27]The very similar orbitals are LUMO+7 for formamide–H2O complexes,and LUMO+9 for formamide-(H2O)2complexes. All thesea′orbitals are concentrated along the C–N bond,and could be a pathway to the breakage of the C–N bond. The plots of these orbitals for formamide,A and D are also shown in Fig.6. It is noted that we do not show the correspondingπ∗andσ∗resonant MOs for all the complexes because they have almost the same shape. Table 2 shows the SVOE values obtained by using an empirical scaling formula.[39,40]Our SVOE value of 2.09 eV for the lowest unoccupieda′′molecule orbital for formamide is in good agreement with the experimental value of 2.05 eV.[24]However, the value of 10.68 eV for the LUMO+5 for formamide is much lower with respect to theσ∗resonance positions of 14.9 eV computed by Goumanset al.[27]and 15 eV calculated by Homemet al.[26]For complexes B,D,E,F and I,the SVOE values are higher than the isolated formamide. However, for complexes A,C,G and H,the SVOE values are smaller than the isolated formamide. Since the SVOE values for the lowest unoccupieda′′molecule orbital are related to theπ∗shape resonance and these for the relevanta′molecule orbital are related to theσ∗shape resonance,such results indicate that theπ∗andσ∗shape resonances in complexes B, D, E, F and I should destabilize and for complexes A,C,G and H these two shape resonances should stabilize.

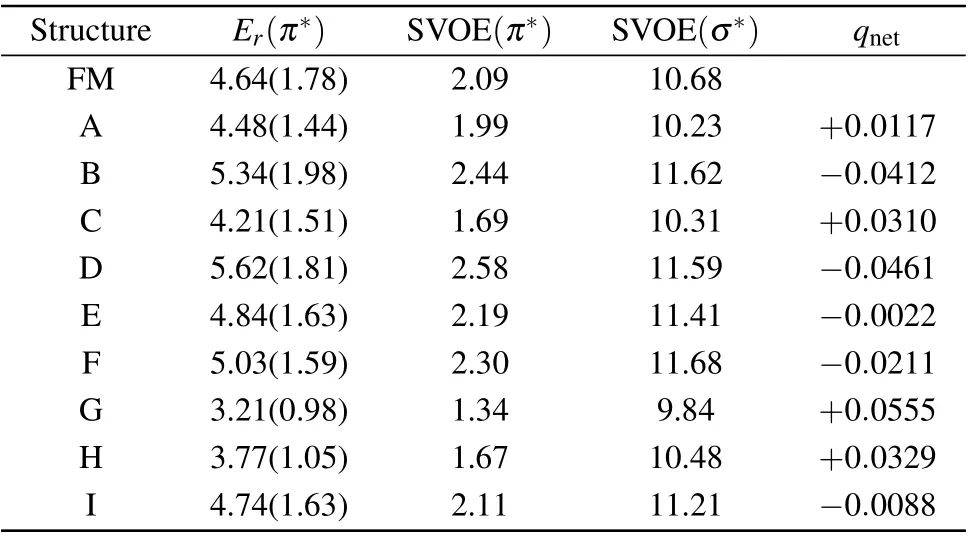
Table 2. Scaled virtual orbital energy (SVOE in eV), the net charge(qnet), and the position (Er in eV) and width (in parenthesis in eV) of the resonance in the SE approximation.

Fig. 6. The left column shows the lowest unoccupied (LU) a′′ (π∗)molecule orbital (MO) for formamide (FM), complex A, and complex D. The right column shows LUMO+5 for FM, LUMO+7 for complex A,and LUMO+9 for complexe D.

In the following, we would look at the net charge of the solute considering the complexes with one and two water molecules. We performed the Mulliken population analysis with the 6-31G(d)basis set at B3LYP/6-311++G∗∗optimized geometry, and the net charge of each an atom of the solute was summed. The obtained net charges for all the complexes are shown in Table 2. The results show that the net charge in the solute of complexes B,D,E,F and I is negative,while the net charge in the solute of complexes A, C, G, and H is positive. The resonant orbital in the complexes is mostly localized on the solute, as shown in Fig. 6. As a result, the incoming electron feels a more attractive electrostatic potential for a positive net charge solute,leading to the stabilization of the resonance for four complexes A, C, G and H, where the water plays mainly the role of proton donor. In the contrary,a negative net charge of the solute represents a less attractive electrostatic potential,which would lead to the destabilization of the resonance, as in the case of complexes B, D, E, F and I.Here the electrostatic effects due to the net charge are investigated, and good agreement with our scattering calculation results is found.

Martinet al.[10]investigated the low-energy electron inducing single-strand breaks (SSBs) in DNA, and pointed out the polarization due to the environment may contribute to the stabilization of the resonances and negatively charged sites can lead to the destabilization of the resonances. The final result is determined by the interplay between the polarization effects and electrostatic effects. As shown in Figs. 1 and 2, for four complexes A,C,G and H the water molecules are mainly proton donors in the H-bonding,which is responsible for the positive net charge of the solute. In these cases, both the polarization (due to the surrounding water molecules) and the net charge in the solute may contribute to the stabilization of theπ∗andσ∗resonances.The water molecules play a role of proton acceptor for complexes B and D.However,for complexes E,F and I,one water plays as proton donor and the other water plays as proton acceptor. The final outcome gives a net of negative charge of the solute by the interplay. For these complexes B,D,E,F and I the polarization indicates stabilization while the net charge leads to the destabilization of the resonance. The final answer about stabilization/destabilization of the resonance can be judged from the cross sections obtained in the scattering calculations,as shown in Figs.4 and 5.

4. Conclusion

We have presented elastic cross sections for three structures of formamide–H2O complexes and six structures of formamide-(H2O)2complexes. The scattering calculations have been performed in the SE approximation with the UK molecularR-matrix code for energies up to 8 eV. Our results show theπ∗resonance of the formamide molecule stabilizes when surrounding waters act as the proton donor, and destabilizes when surrounding waters molecules act as the proton acceptor. For the case of one water, if the water is not only the proton donor,but also the proton acceptor,it destabilizes.For the case of two water molecules,when one water molecule is the proton donor and the other one is the proton acceptor,it destabilizes.The current calculations for formamide–H2O and formamide-(H2O)2complexes show that the effect of water is approximately additive. In addition, how the microhydration environment affects the width ofπ∗shape resonances is also investigated. We find that the surround water molecules can strongly affect the lifetime of the resonance and the related DEA process.

The lowest unoccupieda′′molecule orbitals of the complexes are localized on the solute and show the sameπ∗character of the LUMO of the isolated formamide molecule.LUMO+5 for formamide, LUMO+7 for formamide–H2O complexes and LUMO+9 for formamide-(H2O)2complexes have the same shape and are the resonantσ∗orbitals. We have explored the effect from the net charge of the solute that may affect theπ∗andσ∗shape resonances. Both polarization and positive net charges can contribute to the stabilization of the anion state. A negative net charge may cause destabilization of theπ∗orσ∗resonance. The change from gas to the condensed-phase and the effects induced by the microsolvation in electron-molecule calculations are important steps in understanding how the environment may affect processes in DNA driven by electron collisions and anion states. The present results, although carried out for a simple molecule,represent a clear invitation for additional studies aiming at resonant dissociation of wet biological molecules by low-energy electrons.