Quantum reflection of a Bose–Einstein condensate with a dark soliton from a step potential∗

Dong-Mei Wang(王冬梅), Jian-Chong Xing(邢健崇), Rong Du(杜荣),

Bo Xiong(熊波)2,†, and Tao Yang(杨涛)1,3,4,‡

1Shaanxi Key Laboratory for Theoretical Physics Frontiers,Institute of Modern Physics,Northwest University,Xi’an 710127,China

2School of Science,Wuhan University of Technology,Wuhan 430070,China

3School of Physics,Northwest University,Xi’an 710127,China

4Peng Huanwu Center for Fundamental Theory,Xi’an 710127,China

Keywords: Bose–Einstein condensate,dark soliton,quantum reflection

1. Introduction

Quantum reflection is a classically counterintuitive phenomenon whereby particles are reflected from potential barriers or wells without reaching a classical turning point.[1,2]Such a phenomenon has been observed in various systems,such as atomic mirror,[3–5]nanoporous media,[6,7]rough surfaces,[8]and Si,BK7 glass surface.[9]Recent developments are extended to cold atomic systems in which quantum reflections of ultra-cold atoms appear on the potential of solid surfaces[10,11]as well as on the various structures, such as graphene,[12]semiconductor superstructures and thin films.[13]Since significant reflection occurs under the conditionφ(k)=(1/k2)dk/dxs∼dλ/dxs≫1,[9]where the local wave number,k= 2π/λ, depends on the de Broglie wave lengthλ,andxsis the normal distance from the atom to the surface,the system of ultracold and quantum degenerate atomic gases with large de Broglie wave lengths is an excellent platform for experiments to study quantum reflection at normal incidence with large flexibility on the control of the atomic motion.

Solitons are self-reinforcing wavepackets, which maintain their shapes when propagating over long distances, and emerge from collisions unaltered.[14,15]The existence of such localized wavepackets indicates nontrivial effects from nonlinear interactions, and they have been observed in different systems, including water waves,[16]plasmas,[17,18]and nonlinear optics.[19,20]Theoretically, solitons in nonlinear media were described numerically[21]and analytically[22]half a century ago, and have been confirmed in different fields such as oceanography, biology, and fiber optics. Afterwards, the atomic solitons were also investigated in various platforms,such as optical systems,[23]magnetic films,[24]and waveguide arrays.[25]Recently,solitons in ultracold atomic systems,e.g., Bose–Einstein condensates, have attracted much attention. Especially,such solitons can theoretically be interpreted well by the well-known Gross–Pitaevskii(GP)equation.[26,27]Experimentally, a matter-wave dark soliton with a phase difference ofπcan be generated readily by appropriate phase imprinting,[28,29]density engineering,[30]sweeping a dipole potential through the condensate,[31,32]as a consequence of quantum shock, and from the local minima of interference fringes.[33,34]

In recent years,a great deal of experimental and theoretical work has been involved with the quantum reflection of condensates. Conventionally,the incident velocity of the condensate has a significant effect on the reflection process,and when the velocity of the condensate is low,an abnormal reflectivity has been observed experimentally.[6,11]The probable explanation attributes it to interatomic interactions,which may lead to nonlinear excitations that slow down the center-of-mass motion of the matter wave and result in disruptions.[10,35,36]Due to the surprising robustness of bright matter-wave solitons,its collision and associated regions of chaotic dynamics have been addressed.[37,38]Also, the quantum reflection of such bright solitons has been discussed intensively.[15,39]Moreover, the dynamics of moving bright solitons in a polarized BEC with spin-orbit coupling has been studied, showing that the speed of a soliton dominates its structure.[40]Both stationary bright solitons and moving bright solitons can be found in a spinorbit-coupled condensate.[41]In contrast to bright solitons,reflection of a dark matter-wave soliton has not yet been well investigated, particularly in its structure. Some theoretical works have addressed the role of the nonlinear excitations,such as dark solitons and vortices, in the quantum reflection of the condensate interacting with a solid surface or a gaussian potential.[42–44]For matter-wave dark solitons in boxlike traps,dissipative reflections occur with soft boundaries.[45]A recent work also shows that the orientation of a two-dimensional(2D) dark soliton can significantly affect the reflection probability of the condensate from a sharp potential barrier due to the rotational symmetry broken.[44]However, the essential factors for such influence have not been clarified. Moreover,influence of a 2D dark soliton,especially its configuration,on the quantum reflection subject to a potential well has not yet been investigated. Correspondingly, differences between the reflections of a BEC with a dark soliton from a potential well and a potential barrier are still unclear. In this paper, we investigate the dynamical behavior of a 2D disk-shaped Bose–Einstein condensate containing a dark soliton separately reflected from square potential wells and potential barriers. We try to find the influence of the orientation angle of a dark soliton,the structure of the potential and the width of the potential variation on the quantum reflection probability.We further use dynamical images of the density profiles of the condensates to reflect the physical mechanism through numerical simulations. The underlying mechanism of the quantum reflection is discussed intensively.

2. Method and simulation scheme

We consider a23Na BEC containingNatoms, which are initially trapped by a harmonic trapping potential of the formVh(x,y,z)=m(ω2x x2+ω2y y2+ω2z z2)/2. Here we choose the trap frequencies to beω=ωx=ωy=2π×10 Hz andωz=2π×100 Hz so that the trap frequency in thezdirection is much larger than those in thexandydirections. One can verify that the chemical potential in the radial directions is much smaller than the confining oscillator energy in the axial direction. Hence, the system can be treated as a diskshaped 2D condensate. The dynamics of such a system at zero temperature are well described by the 2D time-dependent GP equation

We consider two different potential profiles: potential I [Fig. 1(a)] is a potential barrier of widthd; potential II[Fig.1(b)]is a potential well of widthd. The abrupt change of the potentials chosen here fulfills readily the quantum reflection condition and makes the reflection of solitons prominent.Thus it enables us to identify the key physical processes occurring when the BEC experiences reflection, and to sharpen the understanding needed for experimental studies to explain BECs with solitons reflected from more complex semiconductor surface potentials or nanostructure potentials. The center of mass of the condensate is initially placed at the position(∆x,0)away from the center of the harmonic trap. In this research,we always consider the normal incident of condensates towards the energy potential surface. Due to the variation of the trap potential, the condensate cloud is driven to move towards the potential barrier or the potential well,which allows us to study the reflection process of the condensate containing a dark soliton. Figures 1(c) and 1(d) show a typical density distribution and the corresponding phase distribution of the initial state of a condensate containing a dark soliton with the orientation angleθ=π/4,respectively. When the solitons are initially imprinted in the condensate,we can freely adjust the angle between the dark solitons and the positivex-axis.

Fig.1.A schematic view of the systems.A condensate cloud containing a dark soliton interacting with a potential barrier(a)and a potential well(b) for the initial center-of-mass displacement in the x direction being∆x. (c) and (d) The top view of the initial density distribution and the corresponding phase distribution of a condensate with the orientation angle of the dark soliton being θ =π/4.

To explore the role of a dark soliton in the quantum reflection of a BEC from potential energy surfaces,it is required that the lifetime of the dark soliton should be larger than the timescale of the reflection process. Since the dark soliton in 2D BECs is generally unstable, it will eventually decay into vortices due to the snake instability. This indicates that the complete quantum reflection should appear before the distortion of the dark soliton. Previous work showed that for some specific parameters the lifetime of the dark soliton either located in the middle of a 2D condensate is larger than the timescale of the reflection process.[44]We also note that the stability of a 2D dark soliton in trapped BECs is still an interesting topic.

3. Results and discussion

Here,we further study quantum reflection of BECs originally containing a dark soliton from an abrupt change of the potential in space, and specifically concentrate on the role of the initial configuration of the dark soliton and the width of the potential variation in such a reflection process. To demonstrate explicitly our findings, we define the time dependent number of atoms on the left hand side of the step function(x ∈[−L/2,0])in the form of

whereLis the size of the system in our calculations. We employRsto denote the reflection probability(asymptotic value ofNl(t))after the condensate cloud has been completely separated from the surface of the potential barrier or well. When the height of the potential barrier or the depth of the potential well,|V0|, is large enough, the condensate cloud undergoes the elastic reflection withRsclose to 1,which is similar to its classical counterpart. For systems without interatomic interactions,the reflection probability depends only on the incident velocity (the displacement∆xof the condensate in thexdirection in our systems). However,for interacting systems,the momenta of thexandydirections can transform mutually during the reflection process,which will in turn affect the dynamics of the system. However, as we only consider the normal incident clouds, there is no initial potential energy in theydirection.

Previous work showed that when a BEC with a dark soliton is reflected from a potential barrier, its asymptotic reflection probabilityRsis highly sensitive to the initial orientation angleθof the soliton.[44]Here we further consider the behavior of such a BEC reflected from a potential well. We find thatRsis still sensitive toθfor potential wells. However,the variation ofRsshows abundant modes with respect to different widths of the potential well. In Fig. 2(a), we show three typical examples of theRs–θcurves for differentd. It is found that the relation betweenRsandθcan be written as

withR0,Rseandλbeing adjustable parameters. Ford=4.2x0as denoted by the red solid curve with squares,the fitting parameters areR0= 0.42,Rse= 0.04 andλ= 2.25, respectively. Ford=4.7x0, the fitting parameters areR0=0.38,Rse=−0.12 andλ=1.61, respectively. This case is similar to theRs–θcurve of the reflection from a potential barrier as shown in Fig.2(b), which can be well fitted by employingλ=2 with∆x=7.05x0,R0=0.935 andRse=0.045. Ford=12.7x0,Rsnearly does not change withθas denoted by the purple solid line with diamonds in Fig.2(a). We note that for both potential wells and potential barriers,θ=π/2, i.e.,the dark soliton parallel to the surface where the reflection occurs is a special configuration. For potential barriers,Rsalways takes the minimum for any value ofdatθ=π/2,while for potential wells,Rsmay take the minimum or maximum according to different values ofd. In Fig. 2(c), we give typical density distributions of the condensate with aθ=π/4 dark soliton (see Fig. 1(c)) during the reflection. For a potential well, the orientations of the dark soliton in the confined part within the potential well(α1)and in the transmitted part of the condensate(α2)with respect to the orientation of the reflected dark soliton may be different from that of the incident cloud(2θ). However, for a potential barrier, the orientations of the dark soliton in the transmitted cloud and the incident cloud are always 2θ.We note that for potential wells,Rsecan be positive and negative,while it is always positive for potential barriers.

In Fig.3, we show the influence of the width of the step potentials in the quantum reflection probability of the condensate cloud containing a dark soliton. We find that when the width of the potential well is less than the length of the soliton(or the condensate),i.e.,d<11.34x0,the reflection probabilityRsis sensitive todas well as the initial orientation of the dark solitonθ. For different initial orientations,Rsdisplays a regular oscillation with an envelope of exponential decay towards a stable value,Rs⋍0.37,whendis larger than 11.34x0as shown in Fig.3(a). It indicates that the reflection probability is immune against the dark soliton configuration when the width of the potential well is larger than the size of the condensate cloud. We note that for a condensate cloud without a dark soliton,the damped oscillation of the reflection probability with respect to increasing width of the potential well has nearly the same period as that of the case with aθ=0 dark soliton (red line with circles in Fig. 3(a)) except for a larger amplitude.is smaller than the decay length, the dynamics of the system are dominated by the decay process, and the effect of soliton structure is strongly depressed. However,fordlarger than the decay length,the orientation angle of the dark soliton becomes significant resulting in different asymptotic values. This analysis coincides with our numerical results shown in Fig.3(b).

Fig. 2. The reflection probabilities as a function the orientation angle of the dark soliton and the typical Density profiles of the system during the reflection process. (a) The curves of the asymptotic reflection probability (Rs) of a condensate reflected from the potential well with respect to the orientation angle of the dark soliton θ. The red solid line with squares, the black solid line with circles and the purple solid line with diamonds are for the width of the potential well being d=4.2x0,d=4.7x0,d=12.7x0,respectively. The blue dashed line and the green dotted line are the corresponding fitting curves calculated by Eq. (4),respectively. (b)The red solid line with squares is the Rs(θ)curve of a condensate reflected from the potential barrier with d=5.64x0,and the black dotted line is the corresponding fitting curve calculated by Eq.(4).(c)The density distribution of the condensate reflected from the surface of the potential well with d=4.2x0 at t =1.68t0,and from the surface of the potential barrier with d =5.66x0 at t =1.68t0. The angles indicated by the white arrows show the directions of the dark solitons in different parts of the condensate cloud. In upper figures, the parameters used for the potential wells are V0=−180E0 and ∆x=7.05x0,and those used for the potential barriers are V0=40E0 and ∆x=7.05x0.

Fig. 3. The reflection probability Rs(θ) and the difference δRs between Rs(π/2) and Rs(0) versus the width d of the potential change. (a)The Rs curved with respect to d for the orientation angles of the dark solitons are 0 (red solid line with circles), π/4 (black solid line with squares),and π/2(blue solid line with triangles),with ∆x=7.47x0 and V0=−180E0. (b)The Rs curved with respect to d for the orientation angles of the dark solitons are 0(red solid line with circles),π/4(black solid line with squares),and π/2(blue solid line with triangles),with∆x =7.05x0 and V0 =40E0. (c) and (d) The red solid lines with squares are the corresponding δRs curves with respect to d of (a) and (b),respectively. The black dotted lines are the corresponding fitting curves.

To see the influence of the orientation of the dark soliton on the reflection probabilities more clearly, we calculate the quantityδRs=Rs(θ=π/2)−Rs(θ=0) for potential wells and potential barriers as shown in Figs.3(c)and 3(d),respectively. TheδRs–dcurve performs a damped oscillation for the potential well(see Fig.3(c)),which is similar to theRs–dcurves in Fig.3(a). This variation can be fitted by the functionδRs=−0.74exp(−0.32d/x0)sin(3.42d/x0−9.38) (the dotted curve in Fig.3(c)). For a potential barrier,δRsdecays exponentially to a nonzero constant with increasingd. It can be fitted well by the functionδRs=0.09exp(−1.67d/x0)−0.09.Compared to the potential barrier,the reflection from a potential well will be much more sensitive to the orientation of the dark soliton if the width of the potential well is smaller than the size of the condensate, where the amplitude of variation can reach up to 25% with respect to the total reflection. As shown in Fig. 3(d), the reflection from a potential barrier is less sensitive toθ,where the amplitude of variation increases exponentially withd, and is less than 9% with respect to the total reflection.

For the reflection of BECs from potential barriers as shown in Fig. 5, no self-interference occurs within the barrier region, which is completely different from the cases of potential wells. With increasingd, Fig. 5 shows the reflection process of the condensate with different orientations for the same potential barrier. When the soliton orientation is parallel to the barrier surface (Fig. 5(Ia)), the soliton structure tends to prevent the return of the reflected wave by barriers due to its self-reinforcement and thus reduces the reflection probability. Forθ=0, the reflection of the condensate can be regarded approximately as the reflection of two symmetric small condensates,and the influence of the dark soliton is trivial. The reflection behavior of the condensate with aθ=0 dark soliton is identical to that of the condensate without a soliton(see Fig.2 in Ref.[45]). Therefore,when a BEC containing a dark soliton is reflected from a potential barrier, the reflection probability forθ=π/2 is smaller than that forθ=0(see Fig.2(c)). Compared to the potential well reflection,the ability of a dark soliton passing through a potential barrier is much weaker. The soliton structure in the transmitted condensate cloud is not obvious or complete as shown in Figs.4(Ic)and 4(IIc).

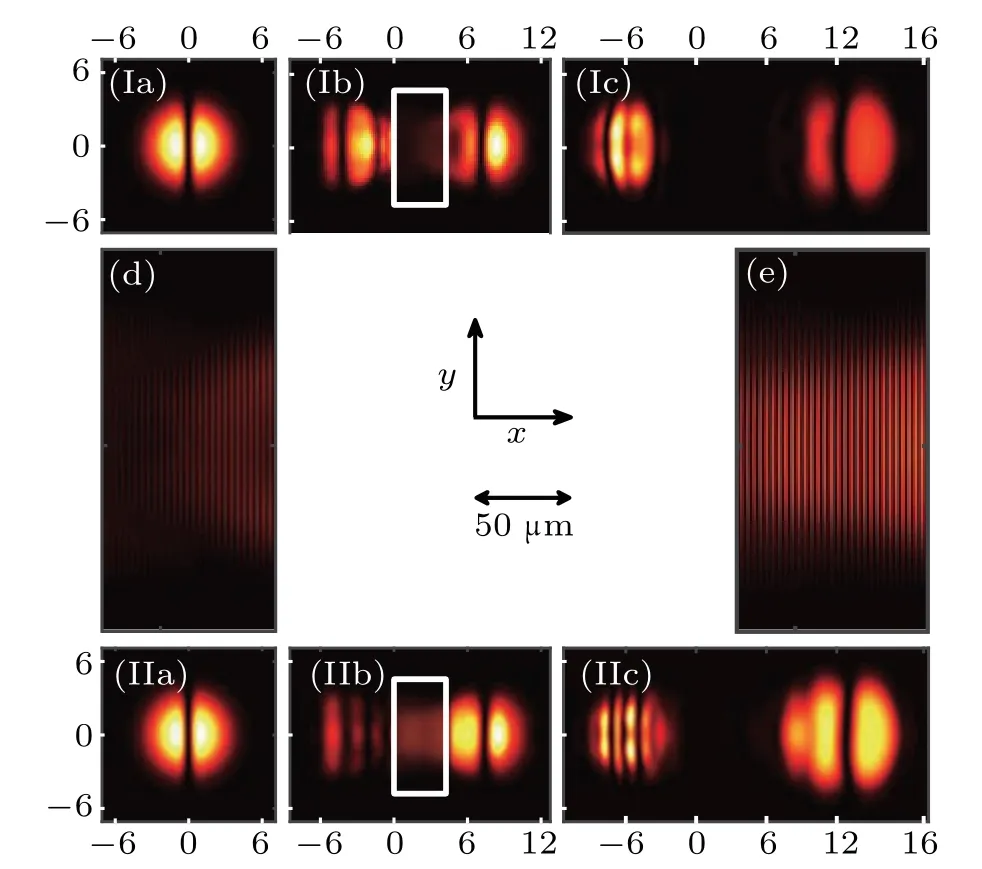
Fig. 4. The typical density profiles of the condensate containing a θ =π/2 dark soliton reflected from the potential wells with two different widths. Line I:the reflection for d=4.2x0. The density distribution of the condensate at t=0(Ia),t=2.16t0 (Ib)and t=2.88t0 (Ic). Line II:the reflection for d=4.7x0,with the corresponding times as the same as those in line I.The depth of the potential well is V0 =−180E0. (d)and(e)Enlarged figures of region surrounded by the withe rectangles in(Ib)and(IIb),respectively.

Fig. 5. The typical density profiles of the condensate containing a dark soliton with different orientation angles reflected from a potential barrier. Line I:the density distribution of the condensate containing a dark soliton with θ =π/2 at t =0(Ia),t =2.40t0 (Ib)and t =3.68t0(Ic). Line II:the density distribution of the condensate containing a dark soliton with θ =0,with the corresponding times as the same as those in Line I.The width and the height of the potential barrier are d=1.41x0 and V0=20E0,respectively.

Moreover, we explore the effects of the expansion motion on the quantum reflection of the system. To clearly isolate the effects,we only consider the potential drop with infinite width. The ground-state BECs are created under different traps:ω=4ω0,6ω0,and 8ω0. The expansion-dominated motion is triggered by changing the trap frequencies rapidly from their original values toω=ω0att=0. Meanwhile,we suddenly displace the harmonic trap by a distance 2.83x0. Thus the condensate expands rapidly when it is accelerated towards the potential drop. In Fig. 6, we show the reflection probabilities of the expansion-dominated BECs,Rs, with respect to different orientation angleθ. We can seen clearly that the shapes of the curves are similar to that of the finite potential well withd=4.7x0in Fig. 2(b) and that of the barrier potential in Fig.2(c). Hereθ=π/2 is still a special configuration with the lowest reflection probability. We find that these curves can also be well described by Eq. (4). However, the curves are much shallow,and the variations ofRswith respect toθare only up to 0.05. We note that the significant difference between the systems with expansion and without expansion is that the sensitivity of the reflection probability to the soliton orientation at infinite width of the well. When the expansion is included,Rsis still sensitive toθat infinite width of the well for the reflections in the potential well systems. This is quite similar to reflections of systems for potential barriers(see Fig.3(b)). Since the expansion results in the acceleration of center-of-mass of the condensate cloud towards the potential drop, the reflection probability reduces accordingly. As shown in Fig.6,Rsfor larger initial trap frequency is smaller than those for smaller ones, due to the fact that the larger the initial trap frequency is,the higher the expansion speed is.

Fig.6. The reflection probability of the condensates dominated by expansion motions from a infinite wide potential drop as a function of the orientation of the dark soliton. The red solid line with squares,black line with circles and green line with diamonds are for systems with initial trap frequencies 4ω0,6ω0 and 8ω0,respectively. The depth of the potential well and the initial displacement of the condensate are V0=−180E0 and ∆x=2.83x0,respectively.The dotted line(R0=0.44,Rse=−0.018 and λ =2.07),dashed line(R0=0.41,Rse=−0.020 and λ =2.24)and dash-dotted line(R0=0.38,Rse=−0.022 and λ =2.28)are the fitting curves calculated by Eq.(4).

4. Conclusion

Acknowledgment

We thank Xue Yang and Wen-Kai Bai for helpful discussions.