基于自组织模糊神经网络的大功率LED 调光模型*
2021-12-22李纪宾饶欢乐王晨钱依凡洪哲扬
李纪宾,饶欢乐,王晨,钱依凡,洪哲扬
(杭州电子科技大学 自动化学院,浙江 杭州 310018)
0 引言
相较于传统光源,大功率LED 具有高光效和灵活可控等优势,在提供交互式或动态照明方面颇具潜力,如建筑照明[1]、太阳光模拟器[2]等。这类光源通常要求光度输出宽范围动态可调,并且快速达到预定的精度要求。尽管LED 自身开关特性可达兆赫兹,但由于系统散热存在时滞、时变不确定特性,使得光度输出规律难以预测。构建可分析、可计算和执行的调光模型对实现更加精细化的调光控制具有重要意义。
经典光电热[3]理论表明LED 结温、光通量、电流存在多参数耦合关系。而后,Tao[4]等人通过机理分析,构建动态光电热模型,用于计算光通量输出随系统温升的衰减变化。文献[5]~[6]考虑环境温度的热因素影响,构建不同操作功率下的线性扰动模型,设计了温度前馈补偿器,以保证光度的恒定输出。文献[7]建立了基于状态空间表达的线性预测模型,便于移植到低成本控制器中去。文献[8]采用多项式插值方法辨识不同驱动电流下的传递函数的零极点增益,构建了线性参数时变模型,但该方法需预先设置整个工作范围的操作条件,计算量较大。尽管LED 物理机制明确,但多数模型[3-6]基于等效阻容网络分析,部分物理量(如结温)并不易于测量,且模型采用离线设计,在长时运行或环境变化较大的条件下将存在失配问题。
自组织模糊神经网络是具有可变结构和参数的非线性逼近器,通过学习规则来刻画非线性模态。聚类技术[9-11]是一种无监督学习的规则提取方法,能够避免人为设定规则的主观性。文献[12]采用误差分级学习机制实现规则生长,文献[13]则基于邻域完备性优化网络结构,文献[14]提出的自组织模糊网络引入了最优脑外科方法修剪冗余规则。这些方法虽能够保证一定的学习精度,但复杂生长和修剪策略降低了学习效率,使网络难以理解和表达。综合上述文献的启发,本文提出一种结合密度聚类、误差和误差率分析的规则生成策略,使模型在精度和复杂度方面得到权衡,并应用于大功率LED调光模型的设计中。
1 系统描述
1.1 LED 光电热分析
LED 是功率型器件,其伏安特性具有类似二极管的负温度特性,通常由如下Shokely 方程描述:

其中,I0是反向饱和电流,Tj是结温,kB是玻尔兹曼常数,q 是电荷,n 是理想因 子,T0是标称温 度,kv为描述LED 在不同结温下的电热漂移系数。
注入LED 的电功率等于发出的热功率和光功率之和:
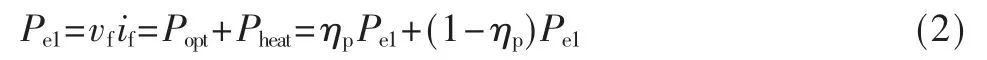
其中,ηp为电光转换效率。由文献[7]有:
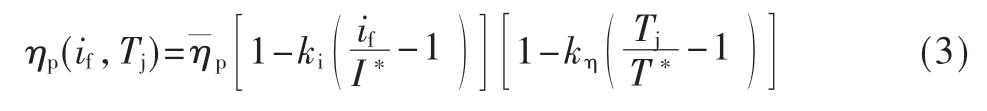
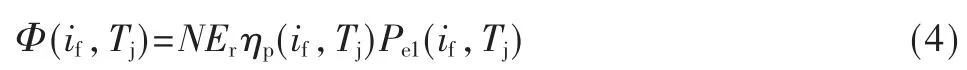
1.2 传热方程
大功率LED 模块通常有单颗或多颗LED 集成在散热器上,其结构和热传递等效阻容网络如图1 所示。其中,Tj、Tc、Ts、Th、Ta分别表示结温、封装外壳温度、导 热体温度、热沉温度和环境温度。在实际工作中,由于热沉热阻远小于空气热阻,使得“LED 结温→散热器→环境”为主要传热路径。
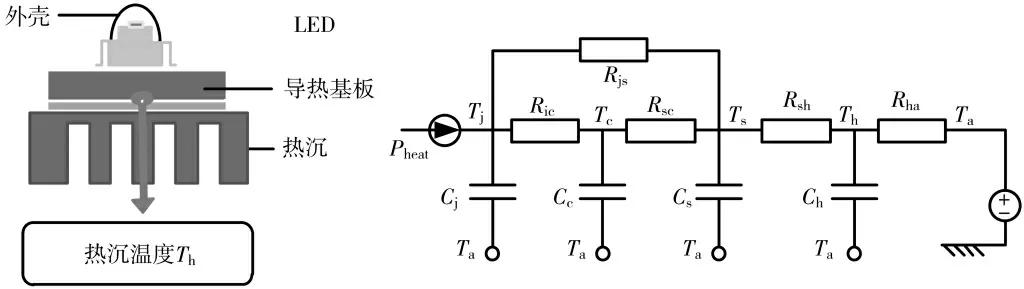
图1 LED 模块结构及其等效传热网络
系统各部分传热方程为:
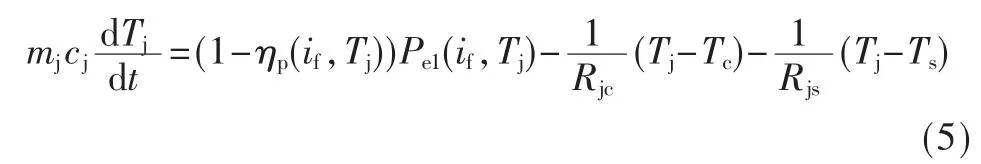

其中,m为等效质量,c为等效热容。符号R,C=mc 分别表示相应部分的热阻和热容。由于二极管和其外壳的热容远小于散热器热容,当采样间隔较小时,其温度变化可忽略。令式(5)、式(6)左边为0,代入式(8)有:
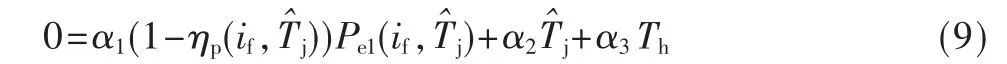
其中,α1、α2、α3为相应的常数项。利用式(9)求解出正 解。结合式(4),得到系统输出总光通量为:

本文将模型(4)~(10)转化为差分形式,作为建模方法数值验证的参考模型,用于产生训练和测试数据。
2 自组织模糊神经网络
2.1 模糊神经网络
基于TSK 型的模糊神经网络结构如图2 所示。
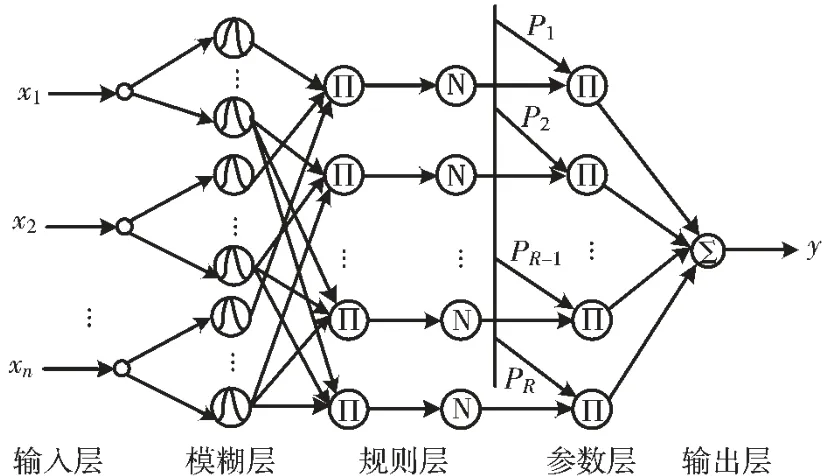
图2 T-S 型模糊神经网络的结构图
第1 层(输入层):将输入变量x 进行归一化处理得到X=[X1,X2,…,Xn]T。
第2 层(模糊层):将输入模糊映射到模糊集上,并采用如下Cauchy 型函数[11]计算隶属度:
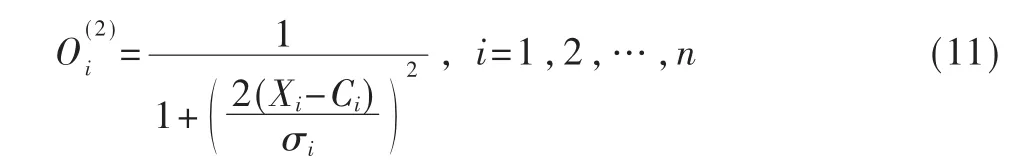
第3 层(规则层):对应if 部分,其节点个数等于规则数R,第l 条规则的点火强度:
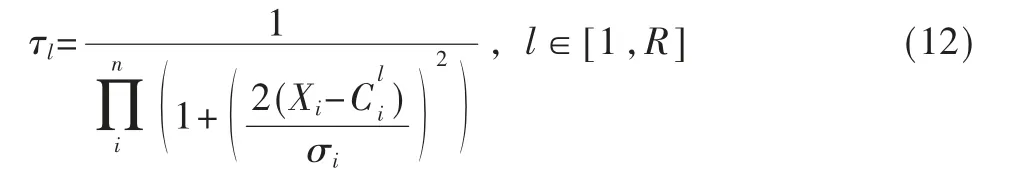
输出为各规则贡献度λl:

第4 层(参数层):对应then 部分多个线性多项式:
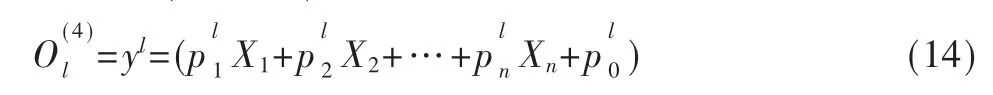
第5 层(输出层):经线性加权得到网络输出:

2.2 结构自组织
2.2.1 规则修正准则
传统方法会导致规则频繁生成和修剪。为提高网络收敛效率,本文引入密度聚类方法来确定规则中心,并用于规则的修正。
设z(k)=(x(k)T,y(k)T)为k 时刻系统输入-输出数据,维数为n和m。当新数据散度值S(z(k))大于或小于所有聚类中心散度值,且位于某一中心领域范围δi=0.5σi,表明该点概括性更强,该点将替代旧规则中心为新规则中心:
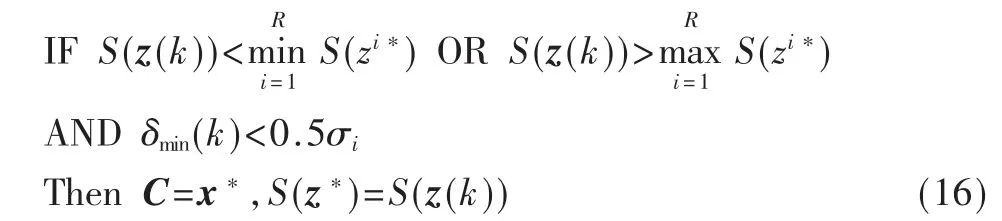
其中,S(z(k))、S(z*)分别表示样本点和聚类中心的散度值,其计算方法可由文献[11]确定。
2.2.2 规则生成准则
定义1(系统误差[15])对于观测数据z(k),期望输出为yr,各规则辨识误差||ei||=||yr-yi||。若||ei||>ke,则考虑生成一条规则:

其中,emin为期望精度,emax为最大输出误差,t为学习时间。
定义2(可容纳边界) 对于观测数据z(k),计算其与规则中心的最小距离:
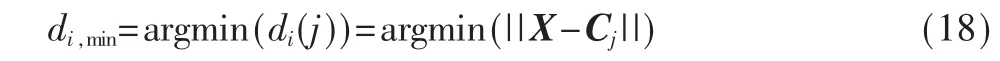
若di,min大于可容纳边界kd,考虑增加一条新规则。
定义3(泛化因子)
第五天清早,我噙着泪水,告别了我的毛毛。走了好远,我回头望,远方那座青山渐渐模糊,山顶那棵黄桷树也只能望见一点儿影子了。这是一块伤心地,我来去匆匆走过一遭,除了把亲生的骨肉撂在这儿,其他么事都冇留下。转身离去,把忧伤撇在身后,我晕晕乎乎地往前走。两天后,我来到了蕲州对岸的长江边儿。坐在江堤上,望着茫茫大江,我的头里边好像也是一片迷茫。我这大老远跑出来是为么事?现在我是要回河浦吗……见到大梁,他会埋怨我吧?我也实在是太对不起他了,狼剩儿冇找到,又把怀的毛毛给丢了,我还有脸再见他吗……江涛声声,江风阵阵,堤脚的防波林,树叶迎风招摇,像一大片绿色的冥幡……
文献[16]泛化因子GF 用于检验模型的泛化能力:

若GF<kGF(kGF为预先设定值),表明现有规则不足,模型泛化性能较差,需考虑增加规则。在本文中,当满足定义1~定义3 中的判断条件时,则生成一条新规则。相应地,网络规则层节点数都会适当增加:

2.3 参数学习
为提高模型抗噪能力,采用带遗忘因子的加权递推最小二乘法(WRLS)对线性参数π 进行估计:
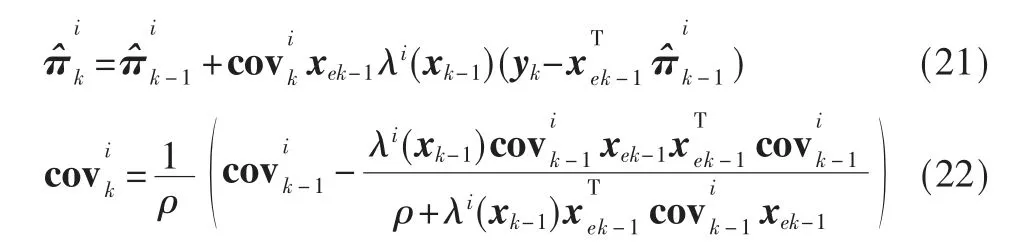
2.4 算法流程
(1)初始化网络参数。
(2)根据输入x(k+1)及规则,输出预测值y(k+1)。
(3)获取新观测数据z(k+1),计算其散度值。
(4)更新现有规则中心散度值。
(5)判断是否满足式(16)前提,若满足,执行后转至步骤(6);否则,判断是否满足式(20)前提,满足则执行。
(6)调整神经元参数σ 及后件参数π。
在各采样时刻,循环执行步骤(2)~步骤(6)实现在线建模。
3 实验与分析
3.1 非线性系统辨识
为验证本方法有效性,考虑如下非线性动态系统:
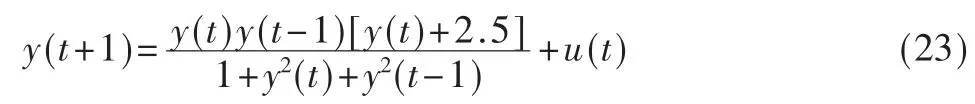
给定输入信号u(t)=sin(2πt/25),初始状态y(0)=0,y(1)=0。由式(23)产生1 000 个样本,前800 个样本用于训练t=1,2,…,800,后200 个样本用以测试其泛化性能t=801,802,…,1 000。网络参数设置如下:ρ=0.95,Ω=800,δ=1.0,emin=0.03,emax=0.5,εmin=0.25,εmax=0.75,kerr=0.001 5,kGF=0.99。
训练结果如图3、图4 所示,表1 给出了与现有模糊网络建模方法的对比,所有算法均采用同样的训练集和测试集。
由图3、图4 可以看出,经过不断的增进式学习,最终生成5 条规则,且测试误差在[-0.001 5,0.001 5]范围内,说明模型具有一定的泛化能力。由表1 可知,相较于仅依据密度聚类eTS 模型、ANFIS 网络以及DFNN 模型,网络结构更加紧凑;尽管模型精度和泛化能力方面稍逊色于GDFNN,但其计算速度更快。因此,本文所提出的模型具有较优的综合性能。

表1 与其他方法的比较

图3 规则生长及RMSE 变化曲线

图4 测试样本拟合曲线及其预测误差
3.2 大功率LED 调光模型
本文采用大功率LED 暖白(CREE family Xlamp Xp-G)作为实验对象,参考模型来自于模型(4)~(8),模型中的热阻、热容等其他参数可由文献[7]及相应的数据手册确定。网络输入为热沉温度Tr、环境温度Ta以及驱动电流If,输出为下一时刻输出光通量预测值。
首先,将模型(4)~(10)转化为差分形式,采样时间设置为1 s,初始热沉温度与室温25 ℃一致,并施加±0.2 ℃的随机干扰噪声。驱动电流以阶跃形式由0.1 A 调至1.2 A,间隔0.3 A,持续100 s;再从1.2 A 下降至0.1 A,间隔0.3 A;模拟LED 由暗至亮再至暗的过程,共产生900 个数据作为训练集。
为检验模型泛化能力,将热沉温度初态值设置为最后一组训练集的温度值,且将室温改变为在26±0.2 ℃区间内。将原阶跃电流信号变更为从0.1 A 到1.2 A,1.2 A 到0.1 A 连续变化的斜坡信号,并将采样间隔缩短为50 s,共计400 个数据用于测试。初始参数设置如下:ρ=0.95,Ω=800,δ=1.0,emin=0.15,emax=0.75,εmin=0.25,εmax=0.75,kerr=0.001 5,kGF=0.99。
图5、图6为在线建模的仿真结果,由图5(a)可以看出,当LED 操作电流在大范围内变化时,不管是训练样本还是测试样本,所建立模型均能准确预测随热沉温度变化引起的光通量变化。由图5(b)可知,仅在操作点变化时会出现较大预测误差,但因引入误差学习机制,模型能够及时修改或生成规则以消除误差。表2 给出一些模型评价指标,其中光通量预测最大误差不超过3%;表3 给出了与其他网络的广泛比较。结果表明,本模型结构紧凑,泛化能力强,能够依据工况变化自适应调整,正确反映光度的动态变化。
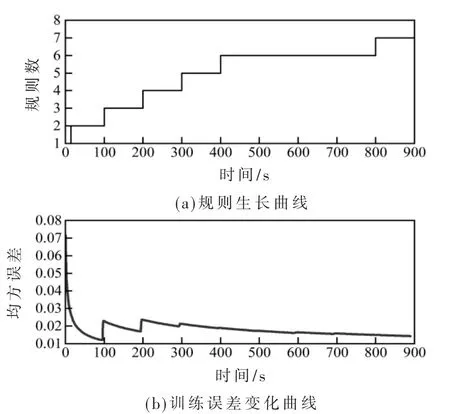
图5 规则生长及RMSE 变化曲线
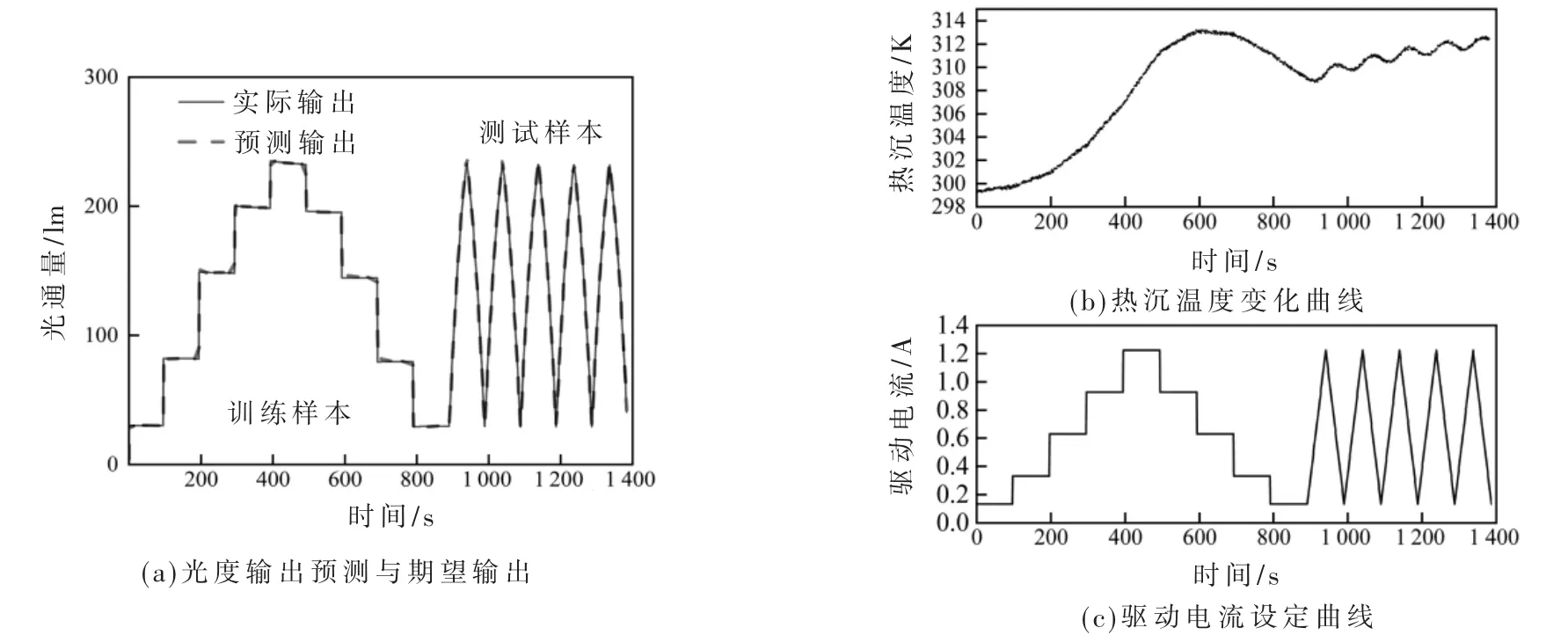
图6 大功率LED 输出光的在线辨识结果

表2 模型的性能指标
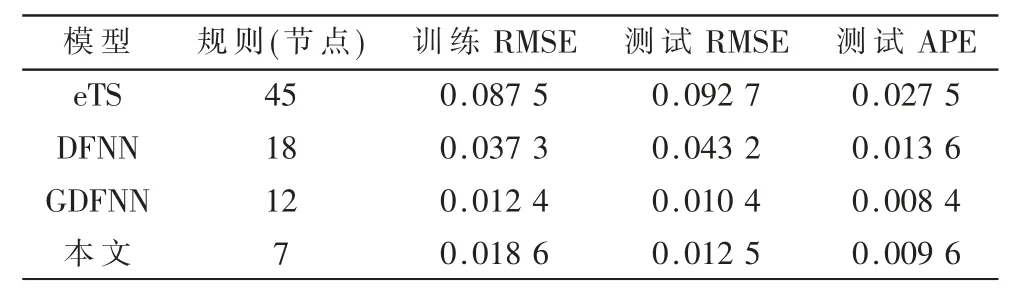
表3 与其他典型方法的比较
4 结论
本文设计了基于模糊神经网络的大功率LED 调光模型。该模型能够准确预测随温度变化的系统的光通量输出,且具有结构紧凑、计算开销小等特点,便于移植入低成本控制器。此外,本文提出算法可进一步拓展,如引入色度、光谱函数等,为实现更优的调光控制提供可计算、可分析和可执行的模型基础。
