遮板型开孔式正方体人工鱼礁流场特性数值研究

2021-12-22李雪艳贾世祥

水资源与水工程学报 2021年5期

王旭，李雪艳，岳峻，贾世祥，战超，王庆

(鲁东大学土木工程学院，山东烟台 264010 )

1 研究背景

随着海洋水产资源的过度开发，海洋荒漠化程度明显加重[1]。海洋牧场人工鱼礁作为改善海洋荒漠化的一种方式受到专家学者的关注[2]。山东省莱州湾明波海洋牧场是国家级海洋牧场，海域内营养盐和饵料充足，适宜海洋渔类生长。近年来，该海洋牧场的经营模式转型升级，除养殖鱼类外还增加了海参等底栖生物。在该背景下，针对明波海洋牧场的现状，亟需开展人工礁体对底栖生物生态恢复效果影响的研究。

目前，国外学者主要探究人工鱼礁与生态效应之间的关系[3-5]。国内学者多采用数值模拟试验[6-11]与物理模型试验[12-17]两种方法来研究人工鱼礁水动力特性。数值模拟试验以其直观、高效的特点在国内得到了广泛的应用。庞运禧等[18]对透空率相同的多种不同结构型式的人工鱼礁进行了数值模拟研究，结果表明迎流角度为90°的礁体有更好的流场分布特征；黄远东等[19-21]对三棱柱型、多孔方型等不同型式人工鱼礁进行了数值模拟研究，同时还探究了开口比对礁体流场分布特征的影响，得到了开口比为0.1和0.2时有较好流场效应的结论。邓济通等[22]通过数值计算探究了布设间距对三棱柱型礁体流场分布特征的影响。总体上，学者们运用数值模拟方法研究人工鱼礁水动力特性的成果较多，也得到了普遍的认可。

基于此，本文在实地调查山东省莱州湾明波海洋牧场的无遮板正方体人工鱼礁基础上，结合海洋牧场实际需求和刺参喜阴的特性[23]，提出了遮板型开孔式正方体人工鱼礁型式，运用数值模拟的方法模拟了不同工况下的流场分布特征，比较了有无遮板及开口比对礁体周围流场特性的影响，以期为人工鱼礁的结构型式设计提供新的思路和参考。

2 鱼礁结构与计算区域

本文共研究了4种开孔式正方体人工鱼礁结构，分别为明波海洋牧场现有的无遮板开孔式正方体人工鱼礁(图1(a))和设计与优化后的3种不同开口比的遮板型开孔式正方体人工鱼礁(图1(b))，同一开孔式正方体人工鱼礁分别在6个面上开有相同尺寸的方孔(图2)，4种开孔式正方体人工鱼礁6个面上的方孔边长为a，正方体人工鱼礁边长为b，遮板向外延伸长度为c，遮板厚度为d，遮板距离礁体底部高度为e，遮板边长为f，鱼礁结构具体设计尺寸如表1所示。

表1 人工鱼礁结构设计尺寸

郑延璇等[24]研究表明，当外部流域长度为9倍鱼礁长度(鱼礁前部长度为3倍，鱼礁本身占1倍，鱼礁后部长度为5倍)、外部流域宽度为6倍鱼礁宽度(鱼礁左侧宽度为2.5倍，鱼礁本身占1倍，鱼礁右侧宽度为2.5倍)、外部流域高度为5倍鱼礁高度(鱼礁本身占1倍，鱼礁上方高度为4倍)时，礁体流场分布特征可以较为精确地呈现。由于本文所研究的4种正方体鱼礁礁体尺寸均为3 m×3 m×3 m(长×宽×高，b=3 m)，因此选取的模拟流场计算域尺寸均为9倍的鱼礁底面长度、6倍的鱼礁底面宽度、5倍的鱼礁礁体高度，即长27 m、宽18 m、高15 m，如图3所示。

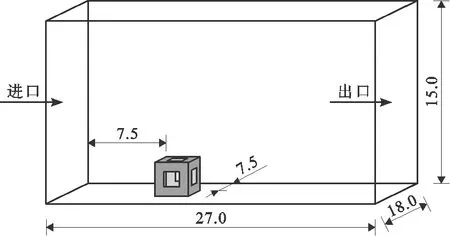
图3 流场模拟计算域示意图(单位：m)

3 数值模型

3.1 控制方程与数值算法

本文中，人工礁体绕流可视为不可压缩流体，其控制方程为连续性方程和不可压缩流体的N-S方程(Navier-Stokes equations)：

(1)

(2)

湍流模型采用RNG(renormalization group)k-ε模型，方程如下：

(3)

(4)

(5)

(6)

式中：Sij为应力张量的平均率，Pa；η为无量纲参数。该两个参数分别由公式(7)～(8)确定。

(7)

η=Sk/ε

(8)

RNGk-ε湍流模型方程中的其他各相关常数取值为：Cμ=0.084 5，Cε1= 1.42，Cε2=1.68，σk=1.393，σε=1.393，η0=4.38，β=0.012。

在压力与流速耦合关系较强的流动中，因SIMPLE迭代收敛速度较慢，故本文基于Fluent平台采用能够克服该缺点的SIMPLEC(SIMPLE-consistent)算法进行压力的修正迭代。计算的最大迭代步数为1 400步。

3.2 计算网格与边界条件

本文采用四面体非结构化网格进行计算的剖分，计算区域网格划分如图4所示，其中最大面网格尺寸为0.25 m。无遮板正方体人工鱼礁的网格数量为991 842个，流域节点数为185 943个；开口比为0.11的遮板型正方体人工鱼礁的网格数为1 158 208个，流域节点数为215 667个；开口比为0.20的遮板型正方体人工鱼礁的网格数为1 161 057个，流域节点数为216 182个；开口比为0.36的遮板型正方体人工鱼礁的网格数为985 697个，流域节点数为183 528个。

图4 流场计算区域网格划分示意图

礁体外部流场区域采用流速入口边界条件，来流设置为均匀流，湍流参数由相应的计算公式给出后续人工输入，来流流速大小共设定为5种，分别为0.2、0.4、0.6、0.8、1.0 m/s；外部流场区域为压力出口边界条件，设置压力恒定且其他参数的压力梯度为0；外部流场区域顶部及两边的壁面采用对称边界条件；外部流场区域底部及数值模型设置为无滑移边界条件。

4 结果与分析

4.1 遮板对绕流的影响

在来流流速为0.2 m/s、礁体开口比为0.36的条件下模拟遮板型开孔式和无遮板开孔式正方体两种不同结构人工鱼礁周围及内部流场，比较分析遮板对绕流流场的影响。

图5为两种不同结构人工鱼礁礁体中心平面上的流速矢量分布正视图。由图5可见，迎流面的水流在接近两种不同结构的礁体时均会产生升高效应而凝聚出上升流，遮板型和无遮板开孔式正方体人工鱼礁的上升流最大高度分别为礁高的1.83倍和1.82倍；上升流致使礁体顶部形成两部分涡流，一部分与礁体顶部开口连接，另一部分在礁体右上部分，且右上部分涡流均向下延伸；遮板型和无遮板开口式正方体人工鱼礁顶部涡流的最大高度距离礁体顶部均为礁高的0.32倍，对于礁体右上位置涡流向下延伸部分，两种结构的人工鱼礁向下延伸高度均为礁高的0.20倍。由图5还可看出，当水流绕过礁体后，两种礁体均在背水面后端产生尾迹流，同时水流减速形成背涡区。其中遮板型开孔式正方体人工鱼礁背涡区形成两股小涡流，整个背涡区长度为礁长的2.11倍，高度为礁高的0.63倍；无遮板开孔式人工鱼礁背涡区形成一股大涡流，整个背涡区长度为礁长的2.12倍，高度为礁高的0.63倍。

图5 两种不同结构人工鱼礁礁体中心平面流速矢量分布正视图

图6为两种不同结构人工鱼礁礁体中心平面上的流速矢量分布俯视图。由图6可见，迎流面水流在接近两种结构礁体时流速会明显减小，同时在礁体两侧和中部开口处各形成流速较大的3股水流；在礁体迎流面两侧产生面积相当的缓流区，中部开口的水流在礁体内部以较高流速流向背涡区；遮板型开孔式与无遮板开孔式正方体人工鱼礁背涡区的最大宽度分别为1.64倍和1.67倍礁体宽度。由此说明，遮板的有无对开孔式人工鱼礁的上升流和背涡流区域面积的大小几乎没有影响。

图6 两种不同结构人工鱼礁礁体中心平面流速矢量分布俯视图

图7为两种不同结构人工鱼礁遮板与礁体底面中间位置所在高度的流速矢量分布俯视图。由图7可见，有无遮板礁体水流均在贴近迎流面时流速减小，同时水流分离在礁体两侧形成绕流，但水流在贴近无遮板开孔式正方体人工鱼礁的迎流面时减速不明显，在其周围产生的缓流区域无明显涡旋，水流在贴近遮板型开孔式正方体人工鱼礁礁体迎流面时减速明显，并在正面迎流处形成小范围涡旋区，经过礁体迎流面两侧绕流时流速明显增大，流速增大的水流在遮板下的礁体之间形成流速明显减小的涡旋，涡旋范围覆盖遮板以下的整个礁体侧面，在礁体背面遮板下也有流速较小的缓流区域。两种不同结构的开孔式正方体人工鱼礁涡动缓流区相关尺寸如表2所示。

图7 两种不同结构人工鱼礁遮板与礁体底面中间位置所在高度的流速矢量分布俯视图

表2 两种不同结构人工鱼礁涡动缓流区相关尺寸

4.2 开口比对绕流的影响

在礁体开口比分别为0.11和0.20、来流流速分别为0.2、0.4、0.6、0.8、1.0 m/s的条件下模拟遮板型开孔式正方体人工鱼礁周围及内部流场，比较分析开口比对绕流流场的影响。

图8为遮板型开孔式正方体人工鱼礁在上述2种开口比和5种来流流速下礁体中心平面上的流速矢量分布正视图。

由图8可见，两种开口比的遮板型开孔式正方体人工鱼礁礁体均在顶部开口与底部开口处形成涡旋，中部进、出水口之间水流流速较大，其流通量与开口的大小成正相关；迎流面的水流在接近两种开口比的礁体时均会产生升高效应而凝聚出上升流，通过分析礁体竖直方向流速矢量分布可知，同一开口比礁体的上升流高度、背涡区长度几乎不随来流流速大小的改变而改变，因此以来流流速0.2 m/s为例，对两种开口比礁体上升流高度进行对比，开口比为0.11和0.20的遮板型开孔式正方体人工鱼礁上升流最大高度分别为礁高的2.18倍和1.92倍。两种开口比的遮板型开孔式正方体人工鱼礁顶部涡流在不同流速下的最大高度距离礁体顶部的距离如表3所示。根据表3可计算出，开口比为0.11和0.20的遮板型开孔式正方体人工鱼礁在不同来流流速下，顶部涡流最高位置距离礁体顶部的平均高度分别为礁高的0.37倍和0.34倍。对于礁体右上位置涡流向下延伸部分，5种流速下开口比为0.11的遮板型开孔式正方体人工鱼礁向下延伸高度均为0.33倍的礁高，开口比为0.20的遮板型开孔式正方体人工鱼礁向下延伸高度均为0.28倍的礁高。

表3 不同流速下两种开口比的遮板型开孔式正方体人工鱼礁顶部涡流最大高度

两种开口比的遮板型开孔式正方体人工鱼礁在5种流速下均在背涡区产生明显的涡旋流态(图8)。以来流流速0.2 m/s为例，开口比为0.11的礁体背涡区长度为2.61倍的礁长，高度为0.79倍的礁高；开口比为0.20的礁体背涡区长度为2.34倍的礁长，高度为0.71倍的礁高。

图8 不同开口比和来流流速下遮板型开孔式正方体人工鱼礁礁体中心平面上的流速矢量分布正视图

前文中的模拟结果已表明，礁体背涡区最大宽度几乎不随来流流速的改变而改变，因此以来流流速0.2 m/s为例，比较开口比分别为0.11和0.20的遮板型开孔式正方体人工鱼礁礁体中心平面上的流速矢量分布，如图9所示。由图9可看出，礁体的开口比越小，则中间水流通量对背涡流区域的面积影响越小。开口比为0.11和0.20的遮板型开孔式正方体人工鱼礁背涡流区域的最大宽度分别为礁宽的2.03倍和1.87倍。

图9 两种开口比的遮板型开孔式正方体人工鱼礁礁体中心平面流速矢量分布俯视图

为探究开口比对遮板以下湍流区域的影响，图10给出了两种开口比的遮板型开孔式正方体人工鱼礁遮板与礁体底面中间位置所在高度的流速矢量分布俯视图，由于遮板以下缓流区域几乎不受来流流速的影响，故图10仍为来流流速0.2 m/s的流速矢量分布图。由图10可看出，两种开口比礁体的迎流面、背流面在遮板以下区域均为流速较小的缓流区，在两侧也均有较大范围的缓流区且形成涡流，不同开口比对礁体遮板以下缓流区域面积影响较小。两种开口比的遮板型开孔式正方体人工鱼礁礁体缓流区相关尺寸如表4所示。