新型网箱浮架系统水动力分析及系泊方式研究*

2021-12-22梁家铭

中国海洋大学学报（自然科学版） 2021年2期

梁家铭, 庞亮, 董胜

(中国海洋大学工程学院，山东青岛 266100)

随着中国人口的增长，海产品需求量日益增多，近海海洋环境污染严重，目前海洋养殖业有向深海发展的趋势，因而网箱将受到更为恶劣海况环境的考验。近年来，网箱的破坏率不断增加，渔民的生命安全和财产安全受到巨大的威胁，为了提高网箱的安全可靠度，加强网箱水动力特性的研究具有重要意义。

一个完整的网箱应该由浮架系统、网衣系统、系泊系统组成，浮架系统是深海网箱重要组成部分，主要为网箱提供浮力，为网衣系统维持有效的养殖体积。浮架系统漂浮于海面上，不仅需要抵抗波浪力的作用，还要承受复杂海流和强风的作用，研究浮架系统在复杂海况下的水动力特性，是提高整个网箱系统的安全性及可靠性的重要途径。完整水动力特性的分析还要包括系泊系统的研究，系泊系统是在复杂环境载荷作用力下提供回复力以保持系泊浮体稳定的系泊方式。许多国内外学者对网箱做了大量研究，早期Slaattelid[1]对一种重力式网箱的浮架结构在不同海况条件下应力特性和锚绳受力特性进行了试验研究。李玉成[2]等将网箱浮架系统简化为一直杆结构，运用数值模拟与物模实验结合的方式得到不同波浪条件下水动力系数，为浮架系统的模拟奠定了基础。基于之前学者们的研究，郑艳娜[3]等对简化后的重力式双排圆形浮架系统在波浪条件下的水动力特性进行了数值分析和物理模型试验，得到了良好的结果。黄六一[4]通过水槽模型试验对方形网箱浮架在波浪下的应力分布，锚泊受力及网箱在水流下容积损失做了定性分析。黄六一[5]对HDPE圆形双浮管网箱水动力特性进行了系统分析并进行了海上实测。孙满昌[6]对方形单体网箱的单锚绳和双锚绳系泊方式安全性进行了计算和讨论，得出了理想条件下双锚绳的最佳布置夹角为22.5°。

目前，70%正在使用的深水网箱为HDPE双浮管圆形网箱(见图1(b))结构[5]，众多学者们对网箱的研究多为圆形网箱结构，虽然它从结构上来说能更好的抵抗外力，但是也有众多局限。方形网箱(见图1(a))在海域中更容易布置组合，有利于合理利用养殖海域，而且作业船更容易停靠及作业，给生产者带来极大方便。本文设计了一种新型方形网箱，利用SESAM进行了频域水动力计算以及系泊条件下时域内耦合分析。现有研究多为规则波下的水动力特性分析，这并不能满足实际海况的特点。本文对新型网箱在不规则波浪条件下进行了风、浪、流共同作用下的耦合分析，对在工作海况和极端海况下的运动响应进行计算研究；与传统的圆形网箱进行了分析对比，得到两种不同形状网箱的运动响应特点；对4种系泊方式进行了计算对比，得到其各自的系泊特性，对实际工程中系泊方式的选择有一定参考意义。

图1 传统网箱结构图Fig.1 Traditional net cage structure diagram

1 网箱模型简介及相关理论

1.1 模型设计

打破了传统网箱的双排浮管结构形式，采用长方形结构形式，为了保证安全性，满足养殖需求和提高工作的方便性，将养殖区域分为3个区域。网箱长36 m，宽24 m，用于工作与堆放养殖工具的边框宽1.1 m。网箱浮架系统结构由平板组成的长方体连接而成，不仅为网箱提供浮力，也用于人行走和放置养殖设备，与传统浮管式的网箱相比，工作区域更加平整，有利于养殖工作的展开。为了满足安全性及强度要求，中间加设圆柱形钢管，由连接装置与四周的板连为一个整体(见图2)。

网箱浮架系统采用玻璃钢材料构建而成，与传统材料相比，玻璃钢具有材料轻、质量高、耐腐蚀、工艺性强等优势，网箱具体参数见表1。

1.2 莫里森公式

网箱的浮架系统尺寸相对于入射波的波长相对较小，即D/L小于0.2，D为网箱浮架直径，L为波长，属于小尺度结构物，采用Morison方程计算浮架结构的波浪力。在波浪和水流的作用下，Morison方程由与流体速度的平方成正比的拖曳力项和与加速度成正比的惯性力项两部分组成，公式可写成：

(1)

式中：ρ为流体密度；CD和CM分别为拖曳力系数和惯性力系数；a和U分别为水质点加速度和浮架结构微元运动加速度矢量；u和U分别为水质点速度和浮架结构微元速度矢量；V0为浮架结构微元排水体积；A为浮架结构微元垂直于流向的投影面积。

图2 新型网箱模型结构图Fig.2 The structure diagram of the new net cage model

表 1 网箱基本参数Table 1 Net cage basic parameters

1.3 运动方程

以重心G为原点的坐标系，浮体的运动方程可表示为：

(2)

本文时域耦合分析中考虑系泊力和环境荷载等非线性因素的影响，采用间接时域法即先求出频域水动力参数，通过FFT傅里叶变化将计算结果从频域转化为时域，采用的运动方程如下所示：

Ffk(t)+Fw+Fc+Fm(t)+Fsd(t)。

(3)

式中：C为浮体的静水恢复力系数阵；x(t)为浮体6自由度位移；Fsd(t)为二阶波浪漂移力；K(t-τ)系统的延迟函数矩阵；其他字母含义与公式(2)相同。

2 水动力分析

2.1 计算流程简介

DNV船级社的SESAM软件是水动力分析领域认可的有限元分析软件，其显著特点是功能模块化，首先在HydroD进行频域内的水动力分析，得到水动力参数以及网箱浮架系统在自由漂浮运动状态下规则波中的运动响应，可由响应幅值算子RAO(response amplitude operator)表示，然后以频域内分析得到的水动力参数为基础，导入DeepC中进行时域耦合分析，得到6自由度下响应以及锚绳受力等时域计算结果。

2.2 环境条件

频域分析时，海水密度为1 02 5 kg/m3，工作水深32 m，选定规则波周期1～30 s，前10 步长为0.5 s，后20 s步长为1 s。入射角由0°～360°，间隔15°。

频域分析中网箱浮架系统所受的环境载荷等一些非线性因素进行了线性化的处理，未考虑时间累计效应，因此频域内的分析预报只能大体上预估浮体运动响应，应进一步进行时域分析获得更加符合实际情况的结果。

时域分析中模型添加了系泊系统，所用锚链质量为37.9 kg/m，破断荷载为6.8×104kN。在不规则波下计算浮体的运动响应，波浪谱采用在工程设计中广泛应用的P-M谱。本文分工作海况和极端海况分别进行了计算，根据中国沿海长期分布资料[7]取得两海况的波高、水流、速度等详细数据见表2。

2.3 工作海况计算结果

时域分析时，本文所有的风、浪、流以最不利的方式入射，即风、浪、流按同一方向入射，由于模型为对称结构，入射角选取了0°、45°、90°，工作海况的时域分析的部分结果(见图3)。

表2 时域分析环境参数Table 2 Time domain analysis of environmental parameters

图3 工作海况下时间历程计算结果Fig.3 Result of the device in time-domain under normal sea condition

为了满足生产作业的要求，系泊浮体的纵荡、横荡、艏摇需要限制在水深的10%以内[8]，本文的新型浮架系统在工作海况下的纵荡、横荡和艏摇的最大值分别为2.11 m、0.91 m和0.2°，均小于3.2(水深32 m)，满足生产作业要求，因此新型浮架系统在工作海况下能安全工作。

2.4 与传统浮架模型对比

目前广泛使用的深水网箱大部分为双浮管圆形网箱，为了更加全面了解新型网箱结构的水动力特性，以及方形网箱与圆形网箱的水动力特性的差异，本文建立了相同养殖面积，相同材料下的圆形网箱浮架结构进行了对比分析，两模型具体参数见表3。

时域分析中两模型的系泊系统相同，锚绳长度、材料、倾角相同(见图4)。

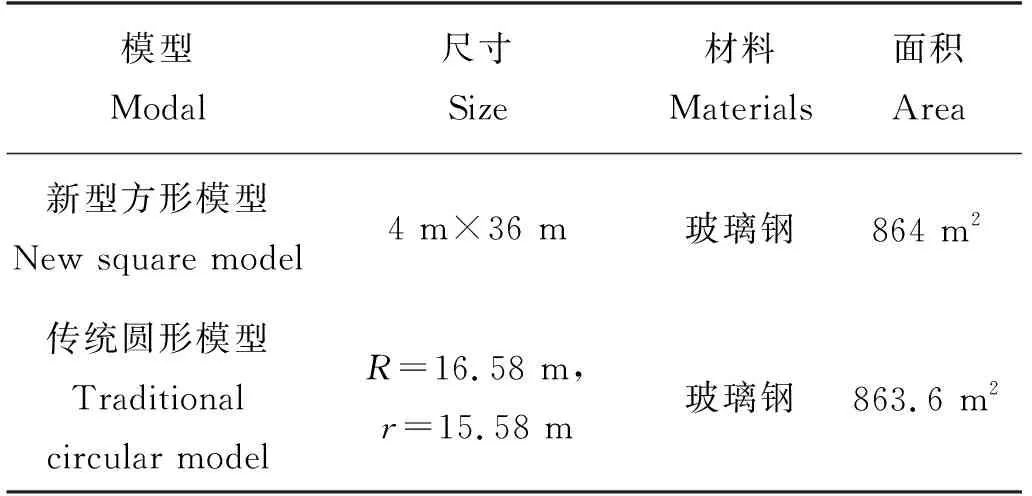
表 3 两模型参数Table 3 Parameters of two modal

图4 时域分析模型图Fig.4 Time domain analysis model

对两种模型进行了频域内水动力计算，得到了不同波浪入射角下6自由度下的运动响应RAO，不同波浪入射角下部分自由度的运动响应RAO对比见图5。分析两模型的结果可知，方形网箱浮架系统在不同自由度下的响应值与圆形网箱浮架系统相比，有不同程度的增大，这说明圆形网箱比方型网箱更加稳定，圆形结构在抵抗波浪力方面更有优势，此结论与赵云鹏[9]的研究结论类似，也说明了本文计算的合理性与准确性。

由于波与波得相互作用产生的非线性影响，不规则波中波浪力包含高频和低频分量，极端海况下产生的巨大波浪力中的高频分量也增大，会对结构物产生高频波浪载荷以及高频运动。观察图5可发现，网箱浮架系统对高频波浪力比较敏感，在高频波浪区产生多个波峰，因此网箱设计应注意避免在极端海况下使网箱发生高频共振响应，也称Ringing现象，从而使结构发生破坏。

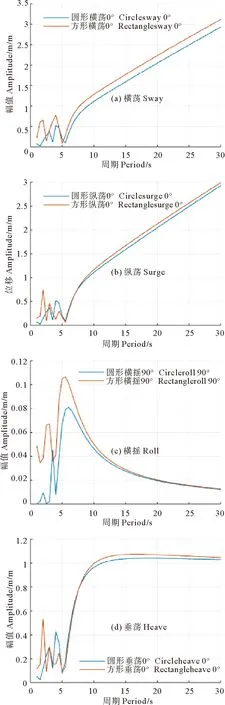
图5 两模型RAO对比图Fig.5 Comparison of RAO between the two models

为了得到更符合实际的计算结果，以及研究在极端海况下的水动力特性，将两模型在极端海况下进行了时域耦合分析，考虑最不利的运动状态，风浪流三因素的入射角相同，由于模型为对称结构，入射角选取了0°、45°、90°，将时域分析中6自由度下的极大值进行了对比(见图6)。

图6 时域运动响应极值对比图Fig.6 Time domain motion response extremum comparison

由图可知，方形网箱比圆形网箱垂荡响应要大50%，波浪力是影响垂荡运动的主要因素，而艏摇运动却要比圆形网箱要小，这是由于两网箱形状不同而造成的差异，方型网箱在艏摇运动下承受的阻力更大；对于横荡、纵荡、横摇、纵摇运动，两网箱的运动响应规律性并不明显，对于0°和90°方向入射，由于方型网箱的长宽不同，其宽度比圆形网箱直径小，而长度比圆形网箱直径大，造成受力面积的差异，因而造成在某些入射角度下，方形网箱比圆形网箱具有更小的运动响应。

时域结果仅比较最大值有一定局限性，为了更好的了解其运动及受力特点，取入射角为45°时两模型部分自由度时域运动对比图以及最大受力锚绳受力情况对比图(见图7)。对于纵荡运动，圆形网箱运动响应明显比方形网箱小；对于横摇运动和最大锚绳受力情况，方形网箱比圆形网箱运动响应略大，差距并不明显。圆形和方形锚绳最大张力值分别为3.3×106和3.5×106N，小于锚绳破断荷载，满足安全性。

图7 时域运动响应对比图Fig.7 Time domain motion response comparison

3 系泊方式的对比

3.1 系泊方式简介

目前海洋工程中常用的系泊方式多为对称系泊，具体分为八字型、交叉型、人字型、平行型，具体结构形式见图8。不同布链方式的优劣，一直是不同风格设计工程师争论的热点，本文对这4种系泊方式进行了极端海况下的时域分析，分析其各自系泊特性。

3.2 计算结果对比

为得到更加全面的结果，入射角分0°、45°、90°入射，其6自由度下的时域分析极值见表4。

由数据可知，不同的入射方向下，运动响应变化很大，说明研究不同系泊系统特性应该综合分析所有入射角下的运动响应。为了更直观的了解每种系泊方式特性，对上表数据进行了统计处理，将表4中4种系泊方式在每个自由度下3个入射角下的最大值取绝对值后相加求取均值，得到的柱状统计图(见图9)。

图8 系泊方式Fig.8 Mooring pattern

分析图9可知“人字型”系泊具有较小的垂荡运动响应，但是有非常大的纵摇运动响应以及相对较大的艏摇运动响应，主要是因为“人字型”系泊在网箱模型上只有两个系泊点，加上模型形状以及长宽尺度的差异，易产生比较大的纵摇和艏摇响应；“平行型”系泊具有较小的纵荡和纵摇运动响应，但有比较大的横荡运动响应，产生此结果的原因是由于平行系泊四根锚绳都是延纵荡方向布置的，从而导致Y方向运动偏小，而X方向运动偏大；“交叉型”系泊的纵摇运动响应较大，说明此系泊方式提供的纵摇恢复力与其他系泊方式相比较小；“交叉型”系泊有非常小的艏摇运动响应，陈徐均[10]基于线性化假设理论推导了交叉型系泊艏摇的回复力矩阵表达式，得到“交叉型”布链方式对于艏摇有很好的控制作用，本文的计算结果进一步验证其结论的正确性；“八字型”系泊方式具有比较均衡的运动响应，属于综合性能较好的系泊方式。