基于DSC模型的黄河入海流路稳定评价指标体系及其应用*

王开荣，毕乃双，杜小康，凡姚申，谢卫明，于守兵

(1. 黄河水利科学研究院水利部黄河泥沙重点实验室，河南 郑州 450003；2. 中国海洋大学海洋地球科学学院，山东 青岛 266100； 3. 华东师范大学河口海岸国家重点实验室，上海 200062)

黄河以水少沙多而著称，历史上输沙量高达10.8亿t/a，就泥沙量而言是世界第二大河，而含沙量位居全球第一[1]。高含沙水体进入地势平缓的下游河道发生快速淤积，形成典型的地上悬河[2-3]，导致河道不稳定性加剧，尤其是入海流路，仅1855年以来就发生了10余次大规模改道[4-5](见图1)，对中国经济社会发展造成显著影响[6]。研究表明：“淤积、延伸、摆动、改道”是黄河入海流路在一定水沙条件下的自然规律[7-9]，从某种意义上而言，黄河入海流路的摆动改道是绝对的，而稳定则是相对的。黄河入海流路的稳定是相对于流路改道而言的，亦即其流路失稳的表现形式是以三角洲摆动顶点(宁海或渔洼)为起始位置的流路大尺度迁徙，而非单一流路范围内的局部出汊摆动和口门迁移。在自然状况下，流路改道的机制与流路出汊机制并无差别，差别在于出汊点位置和影响范围的不同，若出汊点位置在三角洲摆动顶点附近，则视之为改道，若出汊点位置在摆动顶点以下且距离口门较近，则可视之为出汊。

入海流路的稳定问题一直是黄河河口综合治理研究和实践进程中的热点、难点和焦点问题，目前黄河入海流路的稳定与以往自然演变条件下的稳定有所不同，是受制于人工约束指标下的稳定，亦即西河口(二)(以下简称西河口)站(位置见图1)在10 000 m3/s流量时，其水位达到12 m即视为流路失去稳定而进入改道程序(以下简称失稳)[10]。换言之，以往流路的“摆动”和“改道”绝大多数是自然发生的，并没有相应的控制标准，而在20世纪50年代以后，流路的“摆动”、“改道”乃至“出汊”则越来越受到人类实践活动的约束和干预影响。水位变化既是黄河河口演变变化的主要表征指标，也是黄河入海流路实施有计划改道的唯一依据，然而，由于河口水位变化的驱动因子复杂繁多，且其变化十分剧烈，故单纯依靠水位变化的特征值大小将难以科学和客观评判流路所处的稳定状态，基于此，就十分有必要在辨识黄河入海流路失稳驱动因子的基础上，构建基于黄河入海流路客观实际的稳定评价指标体系，以期能够为未来黄河入海流路的规划安排和综合治理提供决策依据。

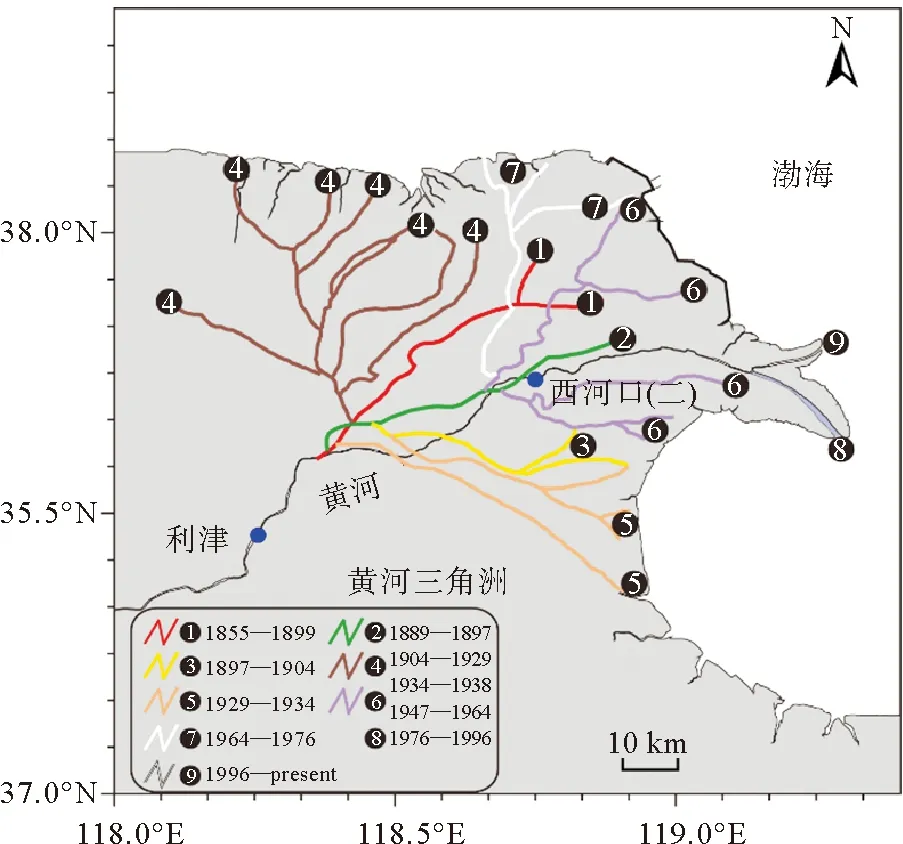
(改绘自文献[5]。Modified from reference[5].)图1 黄河入海流路概况及其改道历史

1 黄河入海流路失稳的驱动因子

已如前述：在自然状况下，流路改道机制与流路的出汊机制并无本质上的差别，因此，籍助于对历次典型出汊过程的分析，就可以从中辨识流路改道(失稳)的驱动主控因子。

纵观20世纪60、70年代黄河入海流路发生的历次自然出汊过程可以发现[11-12]，其出汊的发生一般会有如下四个方面的情形，一是河口沙嘴凸出加剧；二是尾闾流路弯曲加剧阻力增大；三是河槽萎缩，自然悬河加重；四是遭遇漫滩洪水或风暴潮过程；其中，前三个情形均是河床边界条件的变化，其为出汊的发生提供了必要的外部条件，而第四种情形亦即水流动力因素则无疑是出汊发生的主控因子，当然，在某些特定的边界条件下，即使没有漫滩洪水或风暴潮过程发生，河口尾闾河段亦有可能发生出汊，这显然又与水流的顶冲作用方向有关，如1960年8月在四号桩上游1 km处发生的出汊、1963年7月在岔5断面以下发生的出汊即是如此。

显然，入海流路的出汊乃至改道是水流动力与河床边界条件相互约束和综合作用的结果。由于黄河入海流路的尾端高程等同于平均海平面高程，因此，其水流动力作用的强弱可以用河流水位的高低亦即其势能大小来予以表征；同时，水流流向的不同，包括“横、斜河”现象的发生也是衡量水流动力作用的重要因素之一，其代表了水流动力的作用方向，并在一定程度上决定了出汊点或改道点的位置。据此可以明确黄河入海流路失稳的驱动因子及其失稳机制(见表1)。

表1 黄河入海流路失稳驱动因子及其失稳机制

由表1可进一步得出如下认识：(1)基于河口流路不同的区段，其失稳驱动力的来源和驱动因子的体现方式并不一致；其中，径流潮汐段与单纯的径流段相比，其驱动因子的种类和体现方式更多；(2)失稳驱动因子的影响作用和性质也存在较大差异，径流潮汐段的驱动因子只会对该区段的出汊摆动产生影响，而对径流段的改道并无显见的直接影响；(3)不管是径流段还是径流潮汐段，其水位和流向都是其最为重要的两个失稳驱动因子。然而就水流流向而言，在堤防设施日益完善的径流河段，其河势已逐步归顺，发生水流顶冲堤防而导致决口的现象是不现实和难以想象的；而在无堤防保护约束的部分径流潮汐段，因流向变化发生小尺度的出汊和摆动则是被允许的，因此，由这个角度出发，在入海流路失稳的两大重要驱动因子中，水位因子要比流向因子更为关键，这也是选择“西河口站水位在流量10 000 m3/s时达到12 m”作为现行流路改道标准的主要原因所在。

2 判别指标体系构建的理论依据

黄河入海流路稳定判别指标体系的构建必须基于其明确的失稳机制，尽管影响流路稳定的关键驱动因子是以水位高低为表征指标的水流势能，但并不意味着否认河口来沙量巨大、水沙关系不协调是造成入海流路难以长期稳定的症结所在。水位是入海流路演变过程中的主要特征指标，而真正导致水位发生变化的根源在于水沙条件、河道及海岸地貌(边界)条件、海洋动力条件等三者之间的综合作用。基于此，本文建立了以影响因子—泥沙运动—地貌变化—稳定约束边界—失稳驱动力—流路稳定状态为信息链的黄河入海流路失稳驱动力响应模型(见图2)。该系统模型较清晰地反映了流路失稳的过程与机制，可作为构建入海流路稳定评价指标体系的主要支撑链条和理论依据。

基于黄河入海流路失稳驱动力响应模型，可以明确得知：(1)目前，黄河入海流路的稳定可有两条主线路径，其一是基于自然冲决出汊(撕裂)型的稳定，其二是基于人工改道标准型的稳定；(2)现状清水沟流路清7断面以下约70余km的流路尾闾河段属于无堤防工程控制和约束的河段，在遭遇漫滩洪水、发生风暴潮或冰坝壅塞河道并导致水位剧增的情况下，或在发生水流、潮浪冲击自然堤身时，在自然堤相对薄弱的区域则极有可能发生出汊摆动，但这并不影响实践意义上的流路稳定性；(3)入海流路的稳定状态亦即其水位状态是多种影响驱动因子综合作用的结果，其中，水沙因子起主导作用，这种主导作用不仅体现在数量方面，还体现在其水沙组合、过程、动力、流态方面。之所以如此，不仅在于水沙因子是决定河口演变基本特性、塑造河口流路地形地貌包括河床形态、沙嘴形态及流路长度的首要因素，同时也是短时期内影响河口河段水位变化的最直接因素。

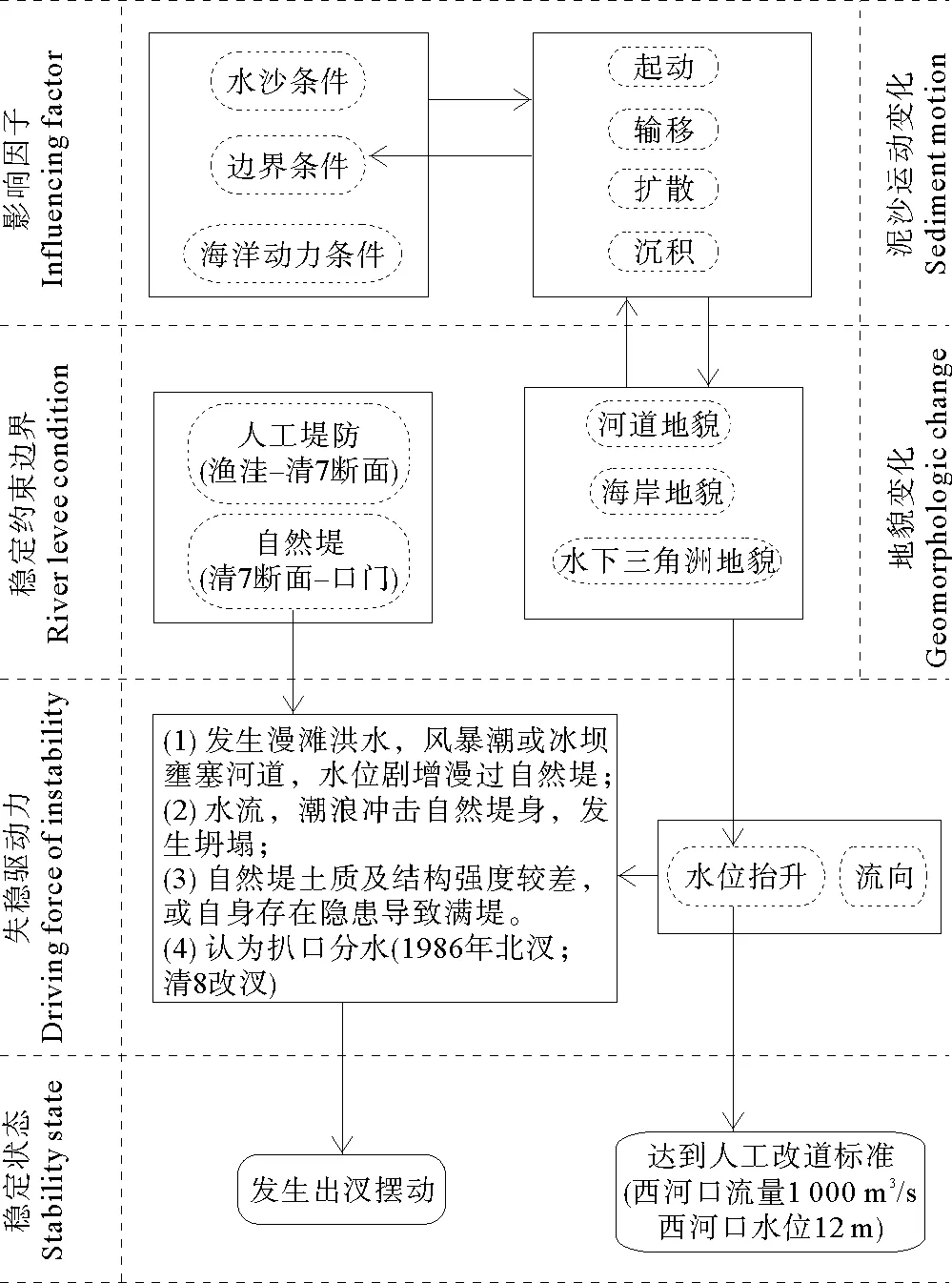
图2 黄河入海流路失稳驱动力响应模型

3 指标体系的描述框架模型和组成因子

3.1描述框架模型

构建黄河入海流路稳定判别指标体系需选择合理的框架模型对其进行描述。目前，PSR模型(Pressure-State-Response，压力—状态—响应模型)因能较好地反映自然与社会之间的因果关系而得到广泛应用[13-14]。随后又陆续出现了SPR模型(State-Pressure-Response, 状态-压力-响应模型)[15]、DSR模型 (DrivingForce-State-Response, 驱动力-状态-响应模型)[16-18]、DSIR模型(DrivingForce-State-Impact-Response, 驱动力-状态-影响-响应模型)[19]、DPSIR模型(DrivingForce-Pressure-State-Impact-Response, 驱动力-压力-状态-影响-响应模型)[20]、DPSRC模型(DrivingForce-Pressure-State-Response-Control,驱动力-压力-状态-响应-控制模型)[21-22]等基于PSR模型的改进模型。考虑黄河入海流路的改道标准以及人工干预对河口演变的影响，本文提出了一种新的PSR改进模型，即DSC模型(DrivingForce-State-Control, 驱动力-状态-控制模型)对其黄河河口稳定判别指标体系进行全面描述(见表2)。

表2 入海流路稳定判别指标体系的构成因子

上表所列内容是根据黄河河口流路演变的基本规律并集成了历年来黄河河口演变与综合治理研究的相关文献而得出的[23-25]，共涉及15个要素、83个具体指标，基本包含了对河口流路稳定产生直接影响或间接影响的相关因子。其中，目标层(A)以流路稳定性综合值为目标，用以判断和衡量流路的稳定状态；准则层(B)包括判别指标体系的驱动力、状态、控制3个方面；要素层(C) 包含了对流路稳定性判别有影响的各类指标类型；指标层(D)则包含了对流路稳定性判别有影响的各类具体指标，并以单值指标为主。

3.2 判别指标体系组成因子的筛选优化及分析

上述初设的指标因子中，可能存在定义有交叉、指标表征内容重复、数量过多等问题，为便于河口流路稳定性的相关计算和状态判别，就需要对指标体系中的指标因子进行筛选、调整、集成和优化，具体步骤如下：(1) 从对水位影响的相关和显著程度加以筛选，摒弃对西河口站水位变化影响作用相对微弱的相关要素，如“海洋动力条件”、“拦门沙特征”等；(2) 选择对水位变化具有控制性和潜在长期性影响的驱动因子；(3) 尽可能用最少量的指标因子去反映事关流路稳定的所有状态信息；(4) 采用的指标因子能够获得相对翔实、准确的数据信息，且容易进行量化操作。据此可得到5个相对独立的对流路稳定具有重大或控制性影响的指标因子(见表3)。

表3 拟定的入海流路稳定判别指标体系的构成因子

表3中设置了“海平面上升”指标，主要基于如下考虑：在黄河三角洲地区，其海平面的变化可同时包括绝对海平面变化和地面沉降，二者的量级相当，甚至地面沉降的影响更加突出[31-32]，而且地面沉降会导致海平面的相对上升以及海水入侵和风暴潮灾害加剧，同时亦会对河口河段的水位乃至流路的稳定产生影响。不过，在10 000 m3/s流量时西河口水位达到12 m的改道标准是基于当地堤防设防标准和河槽行洪能力的关系而制定的，只是一个相对值的概念，从某种意义上而言，在堤防和河槽共同发生沉降的情况下，这一改道标准并未发生变化。此与海平面的绝对上升所导致的堤防设防标准降低有着本质区别。鉴于此，为偏于安全起见，在表3所拟定的海平面变化要素中，并未考虑地面沉降因素，而仅考虑海平面上升因素。

表3中还设置和保留了 “水位波动值”这一指标，设置和保留该指标的主要缘由和依据如下：从宏观的角度而言，黄河河口河段的水位变化将主要受制于入海流路河长的变化[33]，但在一定时期内，同一河长下、同一流量级的水位并非只有一个稳定的唯一特征值与之相对应，而是表现为一个波动区间。因此，“水位波动值”可视为除流路河长以外，其它“短时性、局部性、间歇性”驱动因子对水位变化的影响结果。利用1965—2002年的实测资料，可以点绘西河口在不同年份的3 000 m3/s流量级年平均水位H与其以下河长Lws间的相关关系(见图3)。由图3可以明显看出：在3 000 m3/s流量级条件下，随着河长增加，其水位变化的总趋势是上升的，但对应于同一河长值，却总存在约为0.76 m的波动变化范围，如果将其区分为上升和下降波动幅度，则各为0.38 m，考虑到入海流路稳定判别指标体系的构建主要用于判断水位上升对流路稳定的影响，因此，选择其“上升波动幅度”作为指标体系的构成因子。当然，在入海流路的同一河床断面，不同的流量大小会有不同的水位波动值与之相对应，之所以将3 000 m3/s作为流量级对其水位波动值加以评价，其原因有二：一是在进入河口河段的洪峰过程中，3 000 m3/s流量出现的频次最高，而发生大于3 000 m3/s流量洪峰过程的几率相对较低；二是在传统的黄河水文分析计算中，3 000 m3/s的水位已被广泛采用，且更容易从实测资料中获取准确数值。

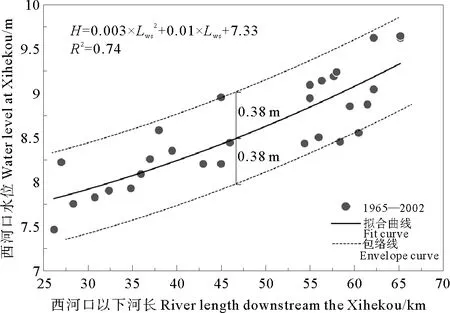
图3 西河口水位站3 000 m3/s流量时的水位与河长关系(1965—2002)

4 判别指标体系的构建及应用

基于对黄河入海流路稳定判别指标体系主控因子的判别和拟定，其指标体系的构建将主要围绕累计来沙量、海平面上升速率、摆动顶点以下的流路长度、水位波动值、河口和段堤防(改道)标准等五个指标因子进行。按照目标特征值的不同，流路稳定判别指标体系可分为基本判别指标体系和综合判别指标体系两种，其中，基本判别指标体系主要表征在10 000 m3/s流量时西河口的水位高低，而综合判别指标体系则主要用于明确流路所处的稳定程度，如下所述：

4.1 基本判别指标体系的构建

已如前述，黄河河口河段的水位升高变化趋势将主要受制于流路的河长变化(见图3)；同时，流路河长的长短又与累计来沙量的多寡密切相关(见图4)。图4中西河口以下河长系利用历年相关航片或卫星遥感解译资料，通过量取西河口站至口门平均高潮线的主流线长度而得到的。

图4 黄河累计输沙量与西河口以下河长关系

在河口堤防设防标准一定的情况下，黄河入海流路的稳定性将主要取决于西河口的年水位升高速率。设定西河口起算年份10 000 m3/s流量时的水位为H0，则当下述公式(1)成立时，则可视为入海流路处于失稳状态，而应实施人工改道。

(1)

式中：ΔHi为第i(i=1……n)年份西河口水位10 000 m3/s的水位升高速率；n为流路的行河年数。

根据图3、4所揭示的相关关系，可以构建如公式(2)、(3)所示的判别黄河入海流路稳定性的基本指标体系；即当第i年10 000 m3/s级流量水位Hi越接近于12 m时，其流路失稳和需要实施人工改道的可能性就越大。其中，得出公式(3)的主要依据有二：一是表3所拟定的入海流路稳定判别指标体系的构成因子内容，二是图3所显示的水位变化与河长变化响应关系的公式表达式。

(2)

Hi=ΔH+HC+HU+C2=K1Lws2+
K2Lws+HC+HU+C2。

(3)

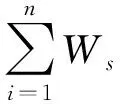
综合上述分析，可构建如图5所示的入海流路稳定基本判别指标体系的构成关系。图中，海平面的上升(Hu)以及流路延伸所导致的水位升高(ΔH)，均意味着河流侵蚀基准面的相应抬高，并通过溯源淤积的形式影响西河口水位；在相对短时期内，这种溯源影响的强度自下而上是逐步衰减的，但在宏观范畴和大尺度时间范围内，这种影响将会波及整个冲积性河流河段，并且表现为近似“平行抬高”的性质[38]。

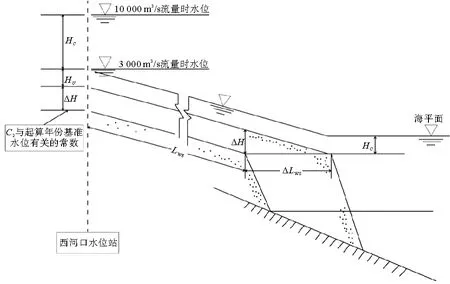
图5 流路稳定基本判别指标体系的构成关系

4.2 综合判别指标体系的构建和评价方法

上述基本判别指标体系可以直观地反映当前距离流路失稳(亦即流路改道)时的10 000 m3/s西河口水位差值，但不能综合评判当前流路所处的稳定状态；基于此，考虑基本判别指标体系所蕴含的主要指标及其相互关系，以水位、河长和累积来沙量三个核心指标建立综合判别指标体系。

(4)

如果所有比较的结果都是准确的，则应该恒有：

αji=αiκ*ακj=αik/αjκi,j,κ=1，2，3。

(5)

这时，称判断矩阵A具有一致性，否则不具有一致性。

在解决实际问题时，由于客观事物的复杂性和人们占有资料的不完全性，对事物的认识难免带有主观片面性和模糊性。由此构造的判断矩阵要完全满足一致性要求是困难的，经常会带有某种偏差，如果偏差太大，则影响决策结果，为了保证决策结果的可靠性，必需把判断矩阵的偏差限制在一定范围内，为此需要进行一致性检验和偏差修正处理。通过重新构造判断矩阵，采用偏差最大项修改法，可以重新得到该判断矩阵的排序权向量W=(w1，w2，w3)T=(0.746，0.167，0.087)T，随机一致性比率(CR)等于0.007 5，小于0.01，满足判断矩阵的一致性要求。

在流路稳定综合判别指标体系中，仅仅得出其不同指标的权重是远远不够的，因为不同指标间的特性、单位与数量级等存在显著差异，无法进行直接比较和综合计算，因此需要对原有的指标值进行标准化计算，使每个变量都处于相对均匀化的数值范围内。

鉴于在黄河河口研究及实践过程中，其水位、河长和累积来沙量都有其相对明确的临界阈值存在，因此上述指标的标准化可以采用相对比值的方法进行计算处理，即：

(6)

式中：X0是评价基准年份实际发生的数值；Xi是评价年份当年实际发生的数值；XC是该指标的临界阈值。

基于指标权重及数据标准化过程，就可以对标准化数据进行综合评价分析。定义黄河入海流路的稳定性状态为Φ，则：

(7)

式中:Wi是对流路稳定影响的权重值；Ai是不同指标标准化后的数值。显然，当某一指标的标准化值等于1时，即预示着单纯从该指标的角度而言，流路已达到改道标准而进入失稳状态。

4.3 现状黄河入海流路稳定状态评价

4.3.1 评价基准年份及基准数值 目前行河的尾闾汊河系1996年7月开始使用的清8汊河，因此，评价基准年份原则上选取1996年。由于1996年系清8改汊的初期阶段，其河道冲淤及其水位、流路河长变化剧烈，而且幅度较大，因此，若将1996年的相关特征值作为流路稳定的评价基准年份数值，那么对流路稳定状态进行判别的准确性和客观性将会受到较大的影响；鉴于此，本次稳定性评价基准数值的选取做如下处理：初始累积来沙量采用1996年8月～1998年10月利津水文站累积来沙量，经计算为7.38亿t；初始河长采用1996年7月改汊以来至1998年的平均河长，采用53 km；至于初始水位，从构建的综合指标体系所表达的内涵而言，其水位应该是指受河长控制影响下的水位，而从1996年以来的河口水位持续冲刷下降的变化特征来看，其受小浪底水库拦沙和调水调沙运用的影响更为明显，受河长影响控制的作用并不显著，因此，为保证该指标所表达涵义的前后一致性，故初始水位可暂时依据初始河长53 km(1996—1998年)采用公式(3)进行计算，在不考虑海平面上升及地面沉降等因素的情况下，可得出西河口站3 000 m3/s的初始水位为8.69 m。同时选取3 000与10 000 m3/s水位差值为1.33 m，该值系依据曼宁公式并利用1998年10月西河口水位站附近河道地形资料以及相应的糙率系数进行演算而得出的；最终得到清8汊河10 000 m3/s的初始水位为10.02 m。

4.3.2 失稳阈值 失稳阈值主要包括改道标准水位阈值、河长阈值和利津站容许的累计来沙量阈值。其中，改道标准水位阈值是十分明确的，即西河口站10 000 m3/s水位达到12 m；对于河长阈值和累计来沙量阈值，以1996年为始算年份，并预期清8汊河流路在2018年的基础上尚可继续行河20余年以上，则1996—2038年海平面上升幅度约为0.15 m；同时，考虑到在达到改道标准时尾闾比降趋缓、滩地糙率增大等因素，故3 000与10 000 m3/s水位差值应比现状有所增大，选取1.5 m，据此利用公式(2)、(3)，可演算得到河长阈值和累计来沙量阈值分别为85.3 km、120.8亿t。

4.3.3 现状10 000 m3/s水位估算 选用2018年作为现状年份，利用基本判别指标体系可以对现状条件下的流路稳定状态亦即10 000 m3/s水位状态作出如下估算：1996年6月～2018年10月，利津站实测ΣWs值为36.44亿t，利用公式(2)得出的流路河长为62.4 km；将此河长代入公式(3)，并取Hc值1.33 m、Hu值0.08 m，则可得到现状条件下的西河口站10 000 m3/s水位为10.52 m，距离12 m标准尚有1.48 m的上涨空间。

4.3.4 流路稳定阶段划分 为更加科学界定和判别流路所处的稳定状态，可依据Φ值大小将流路的稳定状态进一步划分为三个不同的阶段，即“稳定”、“相对稳定”和“失稳”阶段(见图6)。其中，“相对稳定”的概念是基于河口河段水位所具有的波动特性而提出的(见图3)，其所表征的涵义是：在一特定时期内，尽管在发生10 000 m3/s流量时西河口水位低于12 m改道标准，但由于其水位波动上升特性的存在，此时刻水位就有可能触及到12 m改道标准而进入“相对稳定”阶段。进入“相对稳定”阶段的评价指标Φm可用下述方法予以确定。

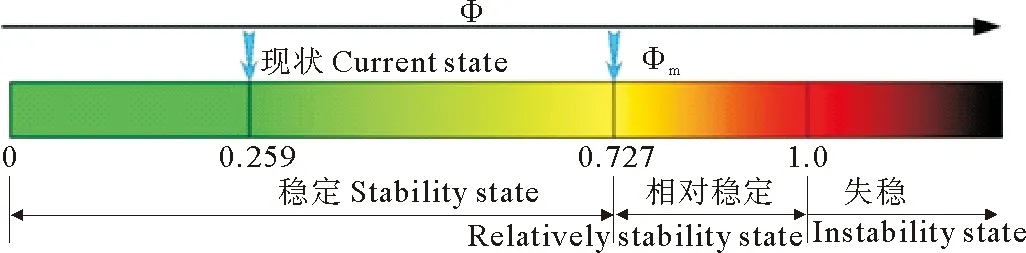
图6 流路稳定阶段划分示意图

拟定10 000 m3/s的水位波动值与3 000 m3/s的水位波动值相同，均为0.38 m，并考虑已有的相关入海流路使用年限研究成果[39-40]，取40年海平面累计上升幅度0.15 m，则可以得出当入海流路进入相对稳定状态时，其相应的10 000 m3/s流量时的西河口水位为11.47 m(12 m-0.38 m-0.15 m=11.47 m)。需要说明的是，水位波动幅度有随流量增大而呈现逐步衰减的趋势，因此，将10 000 m3/s的水位波动值选取为3 000 m3/s的水位波动值是偏于安全的。

单纯依据水位的高低来判断流路是否进入“相对稳定”阶段还不够全面，还需“对等”考虑另外两个指标即河长和累计来沙量的大小来加以综合判别。拟定进入相对稳定状态时的3 000与10 000 m3/s水位差值为1.50 m，利用公式(2)、(3)进行演算，可以得到：当西河口10 000 m3/s的水位在达到“相对稳定”阶段的11.47 m时，其河长和累计来沙量的特征值分别为76.2 km和87.2亿t。据此，即可得到Φm为0.727，见公式(8)。

(8)

4.3.5 现行清8汊河流路稳性状态评价 利用公式(6)可分别得出现状条件下的水位、河长及累计来沙量标准化数值，即，水位：A1=0.251；河长：A2=0.297；累计来沙量：A3=0.256。将上述计算得出的标准化数值及其相应的权重即W1=0.746、W2=0.167、W3=0.087分别代入公式(8)，可得到目前清8汊河流路的稳定状态值为0.259，见公式(9)。这说明：目前的清8汊河流路稳定状态良好(见图5)。

(9)

综合上述相关成果，可得到如下黄河入海流路稳定判别指标体系成果表(见表4)。

5 结语

本文基于对黄河入海流路典型出汊过程的分析，围绕黄河入海流路的失稳主控因子进行了辨识；并以黄河入海流路失稳驱动力响应模型作为理论依据，以DSC模型作为描述框架模型，通过对15个要素、83个具体指标因子的筛选、调整和优化，分别构建了具有不同稳定目标特征值的基本判别指标体系和综合判别指标体系。利用两种判别指标体系对现状黄河入海流路的稳定状态进行了计算判断，结果表明：现状西河口水位站在10 000 m3/s流量时水位为10.52 m，距离12 m改道标准尚有1.48 m的上涨空间，其流路综合稳定状态评价值为0.259，流路稳定状态良好。

按照已有的规划研究成果，现行清水沟流路最终可有三种不同的行河路径，分别是清8汊河路径、北汊河路径和1996年前的原河道路径。上述对流路稳定状态的判别评价是基于现行清水沟流路清8汊河路径的现状所得出的结果；至于其它两种行河路径，尚需根据当时的水沙情势和流路演变特征，依据上述指标体系和评价方法进行稳定状态的判别评价。需要指出的是：清水沟流路的行河年限是上述三条路径行河年限的综合，换言之，只有三种路径情况下的10 000 m3/s水位均达到12 m时，其清水沟流路才算从整体上达到失稳改道的临界状态。

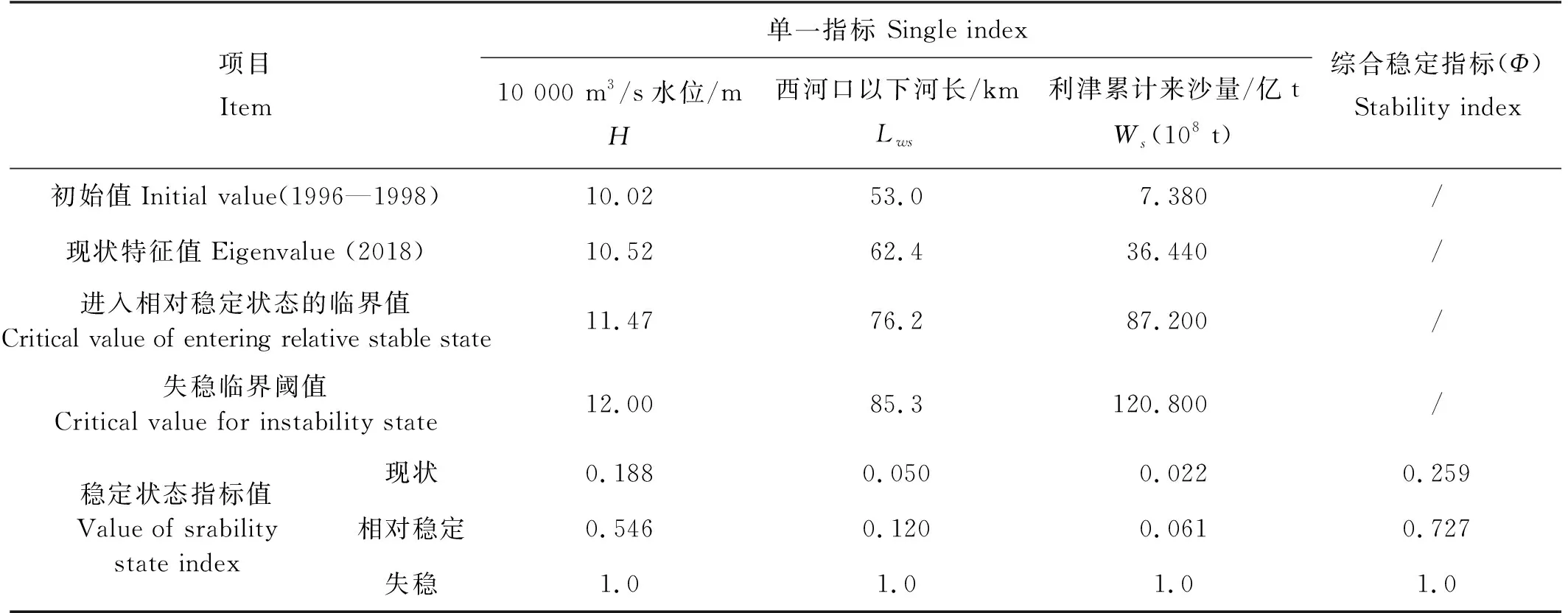
表4 黄河入海流路(清8汊河)稳定判别指标体系成果表

黄河入海流路失稳驱动因子及其稳定判别指标体系的提出，可以对入海流路的稳定状态作出客观判断。然而，该指标体系只是基于人工改道的水位标准而提出的，而对于黄河河口其它类型的稳定诸如河口河道冲淤稳定、口门沙嘴形态稳定、海岸线演化与平衡稳定等还未统筹考虑，此也会给全面和系统评判入海流路的稳定状态带来局限性，亟待进一步开展深化研究。