科技创新、环境规制与海洋渔业全要素生产率

曹 俐，张 晨

(上海海洋大学经济管理学院，上海 201306)

近年来，我国海洋渔业地位不断提高，其产量也不断地增加。2018年，我国海水养殖和海洋捕捞业总产量高达4 768.03×104t，占全国水产品总产量(6 457.66×104t)74%，全社会渔业经济总产值相比1998年增长了近16倍[1]，成为推动渔业经济飞速发展的引擎。然而，我国海洋渔业发展方式仍然粗放，设施装备条件较差，海洋渔业技术创新能力不强，加之近海捕捞过度，环境污染加剧，严重制约海洋渔业可持续发展。沿海地区作为中国渔业经济发展的引擎，其生态环境保护和经济可持续发展至关重要，未来如果不改变传统的养殖和捕捞模式，我国由渔业大国向渔业强国的转变将困难重重。2017年，原农业部颁布《全国渔业发展第十三个五年规划》，强调渔业要遵循“创新、协调、绿色、开放、共享”的发展理念[2]；2019年2月，我国政府还为环境保护划重点，提出坚持生态优先，实现经济与环境保护协调发展[3]；2020年9月，习总书记在第七十五届联合国大会一般性辩论上表示，中国将提高国家自主贡献力度，采取更加有力的政策和措施，二氧化碳的碳排放力争于2030年前达到峰值，努力争取到2060年前实现“碳中和”，即 “3060双碳目标”。 海洋渔业响应海洋产业绿色发展号召，以更小的能源消耗实现更大的经济效益，同时将更多的技术用于环境治理，以促进海洋经济的可持续发展。

“全要素生产率”(Total factor productivity)是指为了符合人类需求而使用生态资源的效率，可以理解为产出与投入的比值。其中，“产出”是指一个企业、产业或一个经济体生产的产品或提供的产品服务价值，即 GDP；“投入”是指一个企业、产业或经济体消耗的资源能源以及由此造成的环境负荷[4]。海洋渔业全要素生产率(Marine fishery total factor productivity，MFTFP)是将全要素生产率的概念运用于海洋渔业，客观来说是在满足人类自身需求的基础上，注重其生产过程中的资源投入及其能源消耗的排放情况，简而言之是转变传统的生产模式，倡导“绿色、优质、节能”的理念。目前，国内外在工业、农业领域对于全要素生产率的研究比较多，对海洋渔业全要素生产率的研究相对较少。海洋渔业全要素生产率受技术进步、科技创新、环境规制等因素影响。其中，技术进步、科技创新(Technical innovation，TI)是影响企业、产业或者区域全要素生产率的关键因素，王樱洁[5]、Moutinho V等[6]选取包括技术进步在内的5个指标，即渔业发展水平、产业结构、对外开放度、能源消耗和技术进步，探究其对渔业全要素生产率的影响，结果显示技术进步和产业结构对渔业全要素生产率的影响最大，能源消耗降低了渔业全要素生产率。环境规制(Environmental regulation，RE)对于全要素生产率的影响效果在时间、强度以及空间方面存在一定的差异性。而技术进步、环境规制与全要素生产率之间也存在相互影响的特征，尤其是环境规制与科技创新之间的相互影响更为复杂。刘阳[7]运用方向距离函数超效率模型和动态面板回归模型检验分析了环境规制、技术创新和渔业全要素生产率各变量之间的关系，得出环境政策可以通过企业的技术创新来提高渔业全要素生产率，即“弱”波特假说成立，但环境规制对科技创新的影响是负向的。

纵观现有文献，对于海洋渔业全要素生产率的驱动机制或者影响机理的研究尚存在不足，更鲜有在空间视角上探究环境规制、科技创新与海洋渔业全要素生产率内在的关系。本文基于面板向量自回归(Panel vector autoregressive,PVAR)模型，实证分析了环境规制、科技创新与海洋渔业全要素生产率三者的关系，旨在：一是测算以渔业经济总产值和渔业碳汇为期望产出指标、以渔业碳排放为非期望产出指标的我国沿海地区海洋渔业全要素生产率；二是运用PVAR模型厘清环境规制、科技创新与海洋渔业全要素生产率之间的关系，为进一步通过环境治理机制推进技术进步、提升沿海地区海洋渔业全要素生产率作政策借鉴。

1 研究方法与数据来源

1.1 PVAR模型

1980年，Sims C A[8]第一次提出向量自回归(VAR)模型，该模型没有任何约束条件，采用滞后项分析内生变量之间的关系。但其涉及的估计参数较多，因而对于小样本数据的测量，精度低且很难达到要求的时间序列长度。为了克服这一缺陷，Holtz-Eakin D 等[9]提出PVAR模型，该模型基于面板数据，综合考虑了个体固定效应和时间效应，通过单位根检验、格兰因果检验、脉冲响应函数、方差分解等方式对数据进行分析，其模型表达式如(1)所示。

(1)

其中，Yi，t表示三维列向量(MFTFP、RE、TI)，即海洋渔业全要素生产率、环境规制、科技创新，i和t分别表示沿海省份和时间；X0和Xj分别为常数项和滞后内生变量的估计参数；p为模型的滞后阶数；σi表示截距项，是沿海11省(市)的个体固定效应；θi，t代表时间固定效应；ε为随机扰动项。

1.2 熵值法

熵值法[10]是一种用于观测指标离散程度的方法，如果一个指标的离散程度越大，表明其对综合评价的影响就越大。本文运用熵值法对各个指标权重进行计算。计算步骤如下：

1)选取n个省份，m个指标，则为第i个省份的第j个指标的数值，原始矩阵Xij(i=1，2……，n；j=1，2，……，m)，即：

(2)

2)指标标准化处理。由于每个指标单位和正负向的不同，无法直接进行计算和比较，因此，需先进行标准化处理，之后再进行权重计算。当指标为正向指标时，其标准化公式为：

(3)

当指标为负向指标时，其标准化公式为：

(4)

当指标为适中型指标时，其标准化公式为：

(5)

其中，di为确定的标准值。

3)为了消除负值，有些指标的值经过标准化后可能会变小或为负值。为了统一和方便计算，对标准化值进行平移处理，从而消除上述情况。

(6)

其中，H为指标平移的幅度，一般取1。

4)利用比重法对数据进行无量纲化：

(7)

5)计算第j个指标的熵值：

(8)

6)第j个指标的差异系数：

gj=1-ej

(9)

其中，j=1，2，……p。

7)第j个指标的权重：

(10)

其中，j=1，2，……p。

8)综合得分为标准化的数据与权重的乘积：

(11)

1.3 超效率DEA-SBM模型

DEA是一种基于投入产出指标对相同类型可比较的单位进行有效性分析的一种方法，它主要包括BBC、CCR、SBM及超效率四种。其中，在分析BBC、CCR、SBM这三者的结果时，如果多个效率决策单元的值同时与1相等，那么就不能分辨这些决策单元效率的高低，而超效率模型能较好地解决上述难题，因此本文选择使用Andersen P 等[11]在1993年提出的超效率DEA-SBM模型，该模型的核心就是当有效决策单元(DMU)的超效率值大于1时，可以对有效DMU进行区分，因此，当DMU效率值大于或等于1时，结论值越大，表明其效率就越高。相应的模型公式如(12)、(13)：

(12)

(13)

本文采用超效率DEA-SBM模型来估算海洋渔业全要素生产率值，在计算过程中，有渔业投入要素，也有产出要素，其中产出要素中包含好的产出(期望产出)和坏的产出(非期望产出)，期望产出越大，非期望产出越小，表明海洋渔业全要素生产率值就越好。故采用非期望产出的超效率DEA-SBM模型来估算沿海各省(市)的海洋渔业全要素生产率。

1.4 指标构建与数据来源

本文遵循数据可行性和科学性原则，根据环境规制与科技创新概念，结合李娇娇[12]和杜军等[13]的研究结果，将环境规制的二级指标设置为环境污染治理投资总额(亿元)、排污费征收额(万元)，将科技创新的二级指标设置为海洋科技专利总发明数(件)、海洋科技课题论著数(篇)、海洋科技类课题成果数(项)，运用熵值法将二级指标综合合并，计算得出环境规制和科技创新指标。

环境规制：环境规制是以保护环境为目的的对各种环境污染行为的规制，分为命令控制型和市场激励型，前者主要是以政府干预的形式实现减排目标，这种政府干预包括事前、事中和事后，其中事中的环境规制成本较高、控制者难以度量、效果不好，事后的环境规制受收费限制，管理面窄，因此本文选取事前的环境污染治理投资总额来度量环境规制，从源头控制排放；后者主要包括排污收费或征税制度、排污权交易制度等，通过企业自身生产方式的转变来降低排放，其中排污收费制度在我国实施时间较长，发展稳定且效果好。因此，本文选取排污征收额(污染处罚)作为环境规制的另一二级指标。

科技创新：科技创新即不同行业用于科技创新和技术开发方面的具体活动，从海洋渔业全要素生产率角度来说，一个行业科技水平越高，其资源利用率就越高，污染排放率也就越低，进一步提高海洋渔业全要素生产率。而海洋渔业全要素生产率的提高则依靠于海洋渔业的科研投入，高水平的科研团队及科技设备对于海洋经济的发展有着重要的影响，故选取海洋科技专利总发明数(件)、海洋科技课题论著数(篇)和海洋科技类课题成果数(项)3个指标作为科技创新的二级指标。

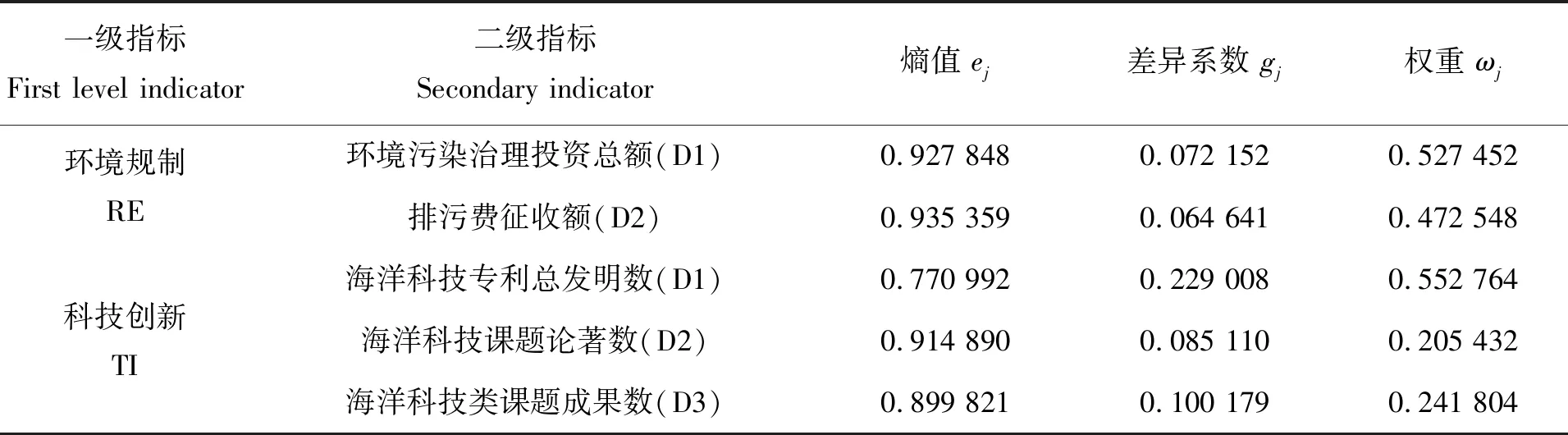
表1 环境规制和科技创新相关指标选择

注：以上所有的环境和科技数据均来自于2003—2018年《中国环境年鉴》《中国环境统计年鉴》及《中国海洋统计年鉴》。由于2019年个别数据存在缺失，因此，本文环境规制和科技创新数据仅至2018年。

Notes：All the environmental and technological data above were from “China Environmental Yearbook”，“China Environmental Statistical Yearbook” and “China Marine Statistical Yearbook” from 2003 to 2018.Due to some missing data in 2019，the data of environmental regulation and technological innovation in this paper only went to 2018.

海洋渔业全要素生产率：渔业总体上可以分为淡水渔业和海洋渔业，本文以海洋渔业为研究对象，研究区域为我国沿海地区，所以本文研究的渔业全要素生产率是海洋渔业全要素生产率。

根据现代西方经济学的观点，劳动力、土地、资本和企业家能力均为生产要素中的一部分，但企业家能力(经费投入)难以衡量，因此，本文选取海洋渔业从业人员数(劳动力)、养殖面积和鱼苗数(土地)、机动渔船总功率和水产技术推广业务经费(资本)作为投入指标。在产出指标方面，以海洋渔业经济总产值和海洋渔业碳汇为期望产出指标，以海洋渔业碳排放为非期望产出指标。由于捕捞业CO2排放占渔业碳排放总量的 70%以上，养殖业是海洋的主要碳汇来源，因此本文借鉴邵桂兰等[14]计算碳排放和碳汇的方法，计算得出所需的期望和非期望产出指标。

本文所采用的数据均源于《中国渔业统计年鉴》(2003—2019)及沿海 11 个省(区)统计年鉴。考虑到本文海洋渔业产出指标包含价格因素，且易受通货膨胀的影响，以实际价格计算不能进行纵向比较，故以 2003 年的渔业 GDP 价格指数为基期，对 2003—2018 年渔业总产值进行平减，得出每年实际数。

2 科技创新、环境规制与海洋渔业全要素生产率的实证研究

本文将沿海11省(市)划分为黄渤海地区(辽、京、津、冀、鲁)、长三角地区(沪、苏、浙)、珠三角地区(闽、粤、桂)，采用PVAR模型，运用软件Stata 15.0从单位根检验、最优滞后阶数、协整检验、GMM估计、格兰杰因果检验、脉冲响应及方差分解7个方面对环境规制(RE)、科技创新(TI)、海洋渔业全要素生产率(MFTFP)进行相关性分析。

2.1 单位根检验

单位根检验的目的是为了避免因不平稳数据产生的伪回归现象，使用最多的检验方法是时间序列单位根检验(ADF)和面板数据单位根检验(LLC)，但ADF检验不适用于面板数据，因此，本文选用LLC检验方法。若检验出来的P值≤0.05，即存在95%的置信度拒绝原假设，则时间序列趋于稳定，表2为LLC检验的结果。

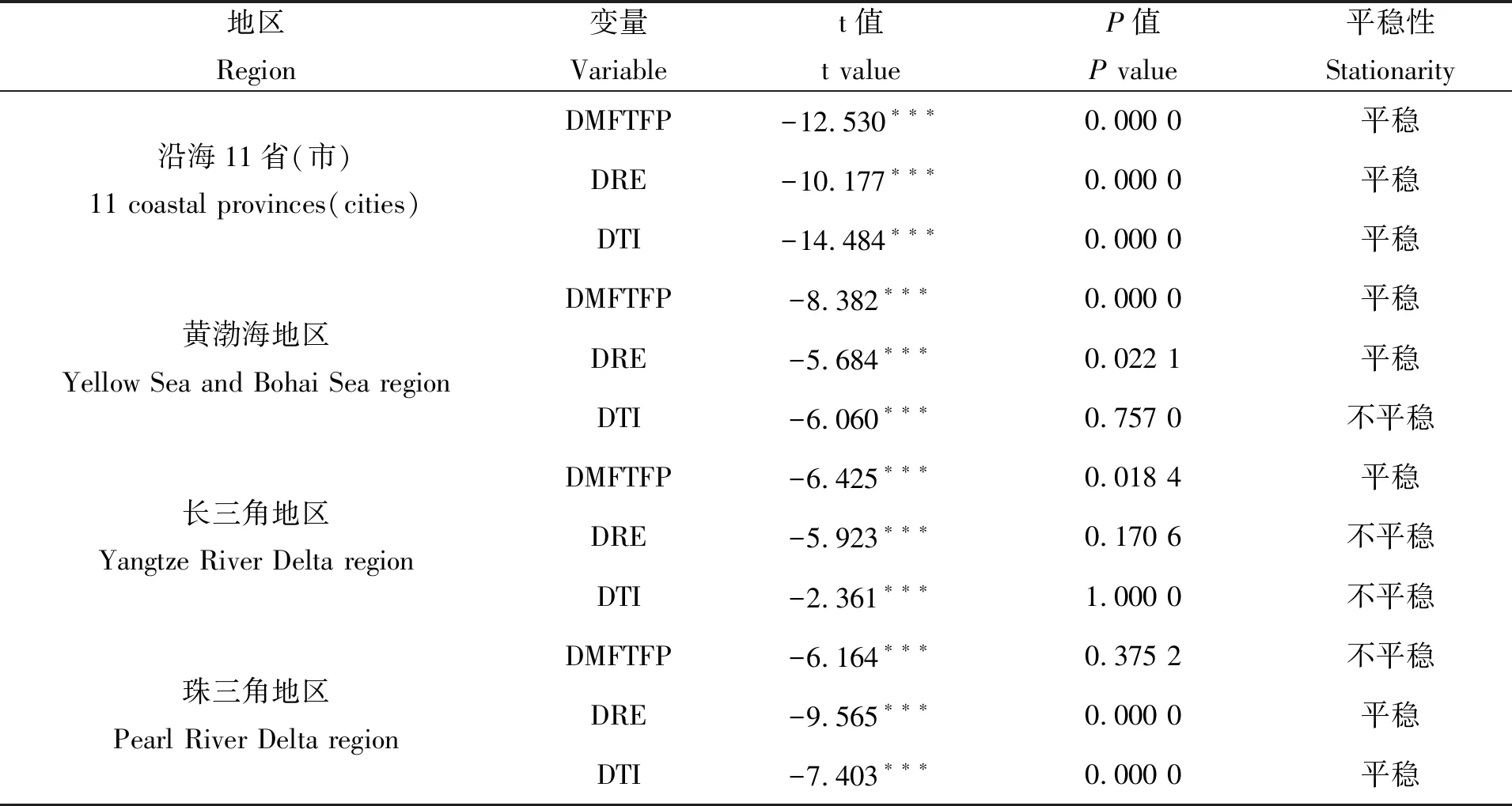
表2 沿海11省(市)及黄渤海、长三角、珠三角地区面板数据单位根检验

注：***、**、*分别代表t值在1%、5%和10%置信水平下显著。变量中字母D表示数据的差分，以下同此。

Note：***，**，and*represented that the t value was significant difference at the 1%，5%，and 10% confidence levels，respectively.The letter D in the variable represented the difference of the data，the same as below.

就整个沿海地区而言，海洋渔业全要素生产率、环境规制和科技创新的t值均表现为1%置信水平下拒绝原假设，说明数据稳定。反观P值，除黄渤海地区DTI、长三角地区DRE和DTI及珠三角DMFTFP的P值均大于0.05外，其他数据均小于等于0.05，说明拒绝原假设的概率为95%以上，数据均为平稳序列。

2.2 最优滞后阶数与协整检验

在对整个沿海地区的面板数据进行平稳性检验之后，还需进一步确定构建PVAR模型中的滞后期。为了确保结果客观准确，一般在选择最优滞后阶数时多采用贝叶斯信息(BIC)、赤池信息(AIC)、准似然独立(QIC)三个准则进行分析，哪个信息准则最小，其就是最优滞后阶数。由表3可知，除长三角地区PVAR模型的滞后阶数为2阶外，其他地区PVAR模型滞后阶数均为3阶，但无论沿海11省(市)还是黄渤海地区、长三角地区、珠三角地区，其PVAR模型的最优滞后阶数均为1阶。

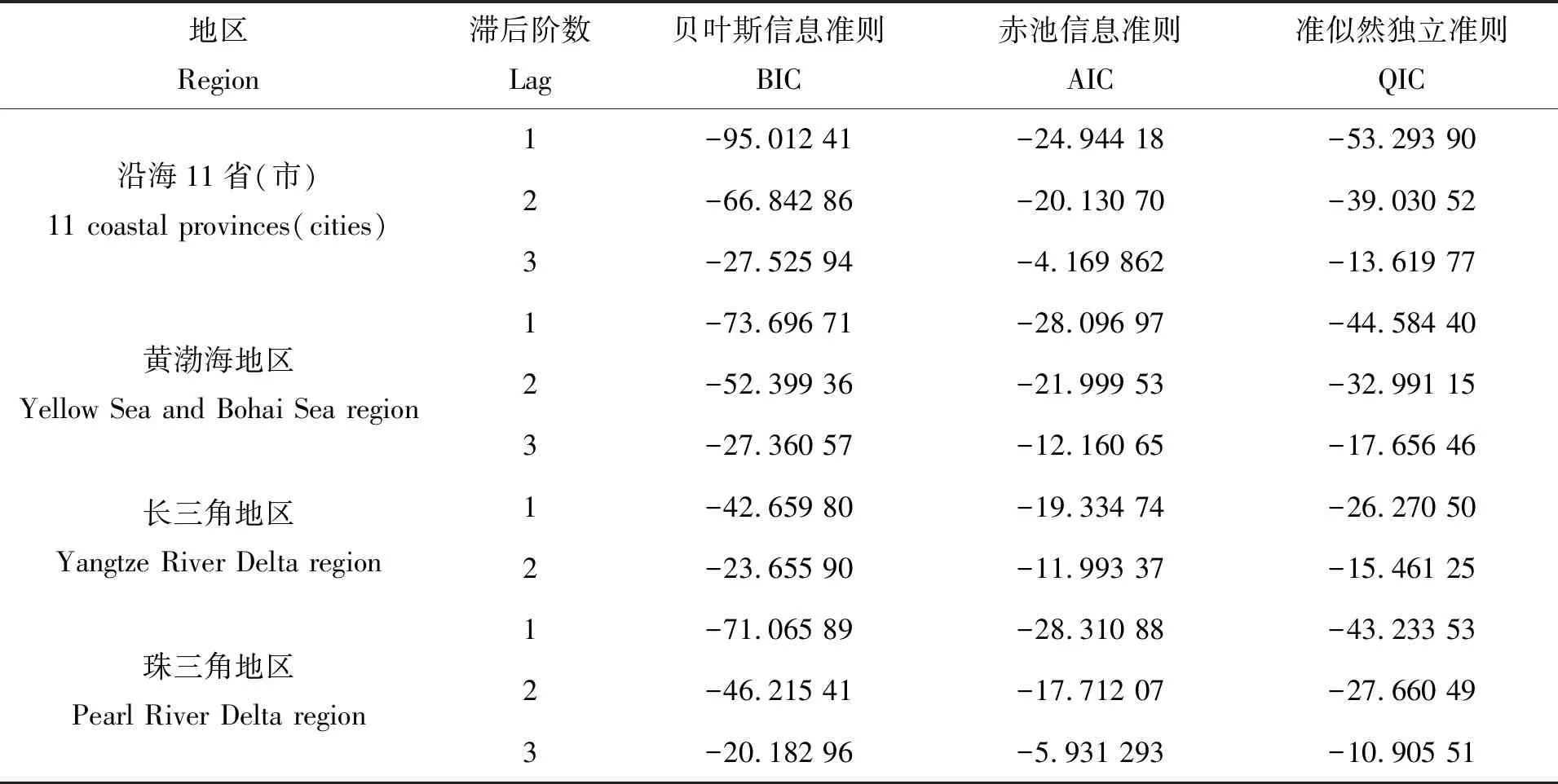
表3 PVAR模型滞后检验

根据最优滞后阶数1阶的检验结果，通过数据进一步分析变量之间是否存在长期均衡关系，结果如表4所示。

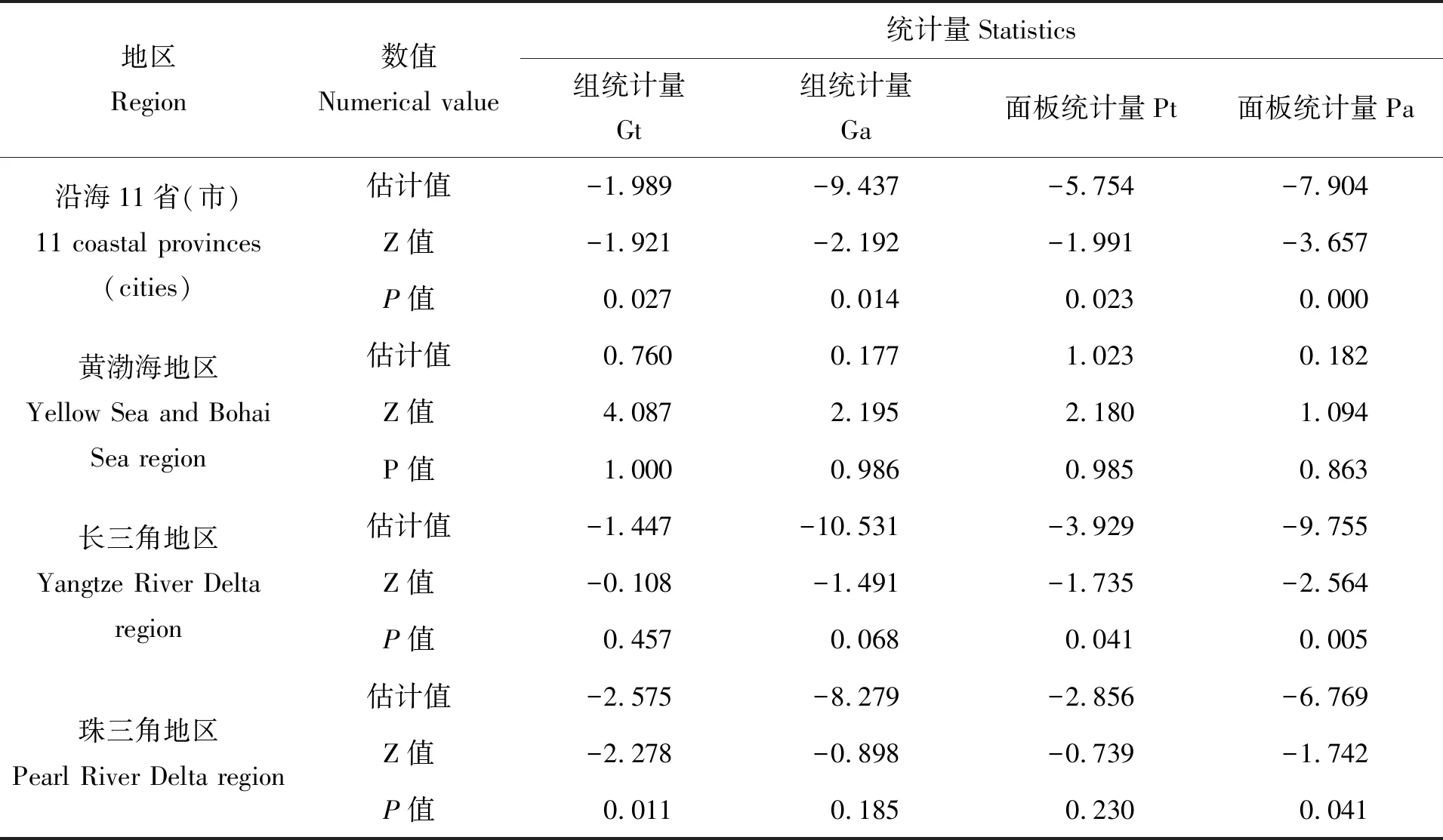
表4 环境规制、科技创新与海洋渔业全要素生产率协整关系检验

注：Gt、Ga、Pt、Pa四个统计量的原假设均为不存在协整关系。

Note：The null hypothesis of the four statistics of Gt，Ga，Pt and Pa were no cointegration relationship.

表4检验结果显示，黄渤海、长三角和珠三角地区各统计变量的P>0.05，拒绝原假设，表明各变量之间存在协整关系，而沿海11省(市)区反之，P<0.05，未拒绝原假设，说明变量之间不存在协整关系。综合黄渤海、长三角和珠三角地区的数据来看，环境规制、科技创新和海洋渔业全要素生产率之间存在协整关系。

2.3 PVAR模型的参数估计

相比传统的计量经济学估计法(如普通最小二乘法)，GMM估计有两个优点：1)它允许随机误差项有异方差和序列相关性；2)准确的参数估计量可以在不知道随机误差分部信息的情况下被得到，结果更为客观。其次，为了避免个体固体效应引起的参数偏差，在模型估计中通常会利用Helmet变换对个体固定效应予以消除，以此来提高模型估计的精度，但由于数据的局限性，本文不采用Helmet对面板数据进行变换，而是对数据直接进行参数估计，估算结果见表5。

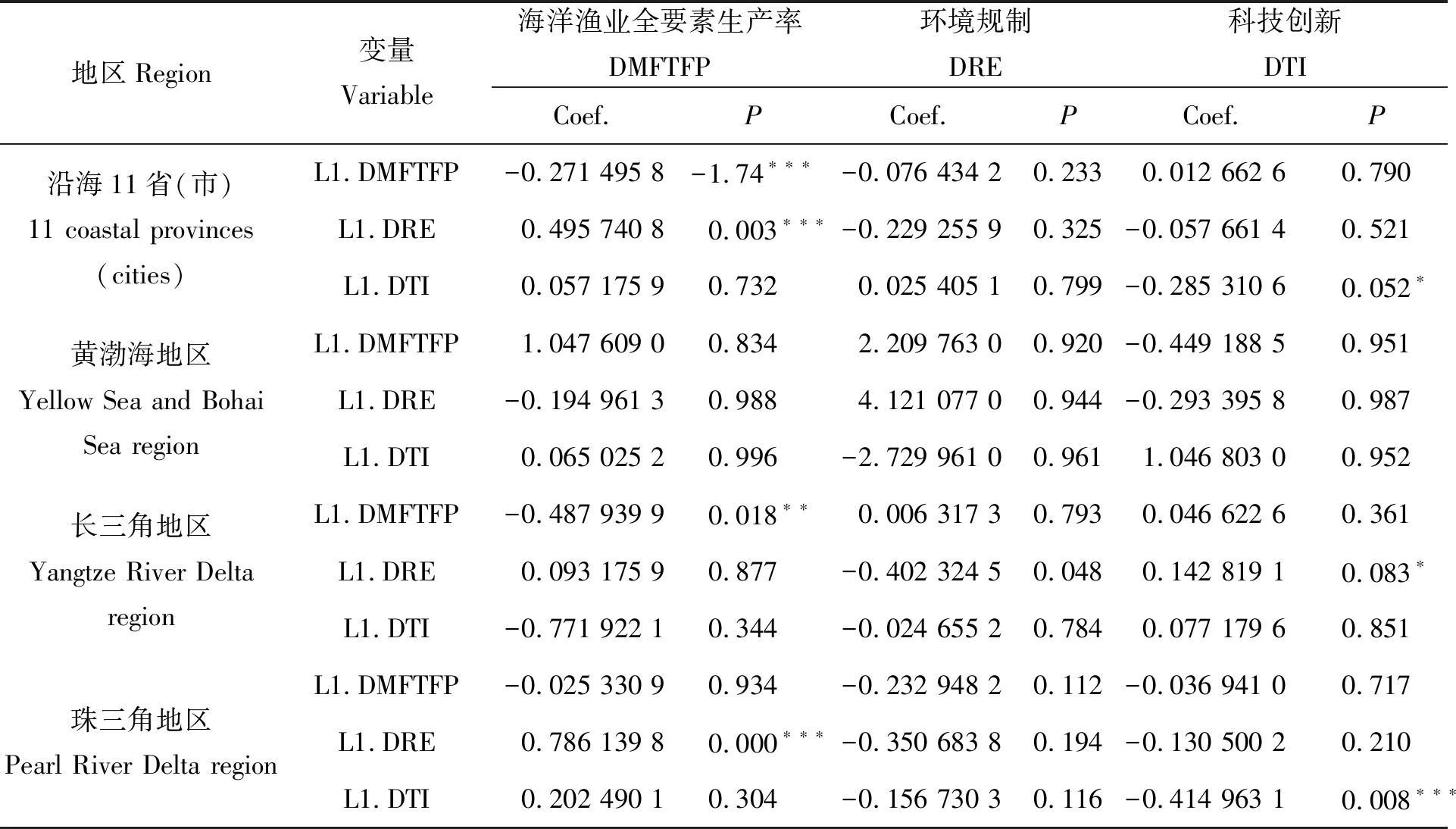
表5 PVAR模型参数估计结果

注：Coef.为GMM估计的系数，***、**、*分别代表在1%、5%、10%置信水平下显著。

Notes：Coef.was the coefficient estimated by GMM.***，**，*represented significant difference at the confidence level of 1%，5% and 10%，respectively.

由表5可知，当海洋渔业全要素生产率作为解释变量时，除黄渤海地区外，沿海11省(市)、长三角地区、珠三角地区的海洋渔业全要素生产率对其自身具有负向作用，且沿海11省(市)和长三角地区表现最为显著，即P值均在1%和5%的置信水平下显著，进一步表明海洋渔业全要素生产率对其自身具有很强的负向作用；而从环境规制角度来说，环境规制对海洋渔业全要素生产率的影响呈现正负交替影响，说明二者之间具有较强的敏感性且环境规制对海洋渔业全要素生产率的影响在短时间内不易表现出来；从科技创新角度来说，科技创新对海洋渔业全要素生产率具有正向的驱动作用，且系数值均小于0，表明在短期内，科技创新对海洋渔业全要素生产率的推动作用不明显。

由表中4个地区的数据可知，海洋渔业全要素生产率对环境规制的作用表现为正负交替，作用力较强，但这种作用力在短时间内难以显现出来；其次，虽然黄渤海地区的环境规制对其自身具有正向作用，但整体上环境规制还是对其自身具有负向作用，只是负向作用表现不明显，说明环境规制对其自身的负向作用不显著；最后除沿海11省(市)科技创新对环境规制具有正向作用外，科技创新整体上对环境规制具有抑制作用，简言之就是科技创新在近期内不利于环境规制发挥作用。

当科技创新作为解释变量时，整体上，海洋渔业全要素生产率对科技创新的作用表现为正向、负向波动，也表明海洋渔业全要素生产率具有潜在优势，而沿海11省(市)、长三角地区呈现不显著的正向作用；环境规制对科技创新的作用是负向驱动，尤其珠三角地区这种负作用时间更长，即环境规制的完善不能加快技术革新，不利于科技创新的发展；就科技创新本身而言，沿海11省(市)、珠三角地区的科技创新对其自身具有负向作用，且二者的负向作用比较显著，而其他两个地区则反之，黄渤海地区的科技创新表现出较强的正向驱动。

探究上述关系表现的原因：一方面与科技成果的转化周期有关系；另一方面，环境治理需要区域之间的协调治理，当前环境跨界合作治理机制的不完善是制约因素之一。

2.4 格兰杰因果检验

稳定性检验仅是PVAR模型估算的第一步，要想进一步研究变量之间的因果关系，还需对变量进行格兰杰因果检验。而所谓的格兰杰因果检验就是有两个变量X和Y，在包含两者过去信息的条件下，对变量Y的预测效果要优于仅用过去Y的信息来预测未来Y的信息效果，即X有助于解释Y的变化，表明X是引致B的格兰杰原因。由表6可得，沿海11省(市)和珠三角地区在以海洋渔业全要素生产率为被解释变量、环境规制为解释变量时，其卡方统计量分别为8.620、13.827，对应的P值为0.003和0.000，故可认为环境规制是海洋渔业全要素生产率的格兰杰原因。类似地，两地区科技创新的卡方统计量为0.118、1.056，P值为0.732、0.304，故可认为科技创新不是海洋渔业全要素生产率的格兰杰原因。但如果变量环境规制和科技创新联合系数显著，则拒绝原假设，即“环境规制、科技创新是海洋渔业全要素生产率的格兰杰单向原因”。黄渤海和长三角地区的格兰杰因果不显著，表明该地区的环境规制和科技创新对海洋渔业全要素生产率提高的促进作用较弱。在以环境规制、科技创新为被解释变量时，对应的P值也都大于0.05，说明变量之间不显著，不存在格兰杰因果关系，但值得注意的是长三角地区的环境规制对科技创新的促进作用在10%的置信区间下显著，表明环境规制对科技创新具有潜在的促进作用。

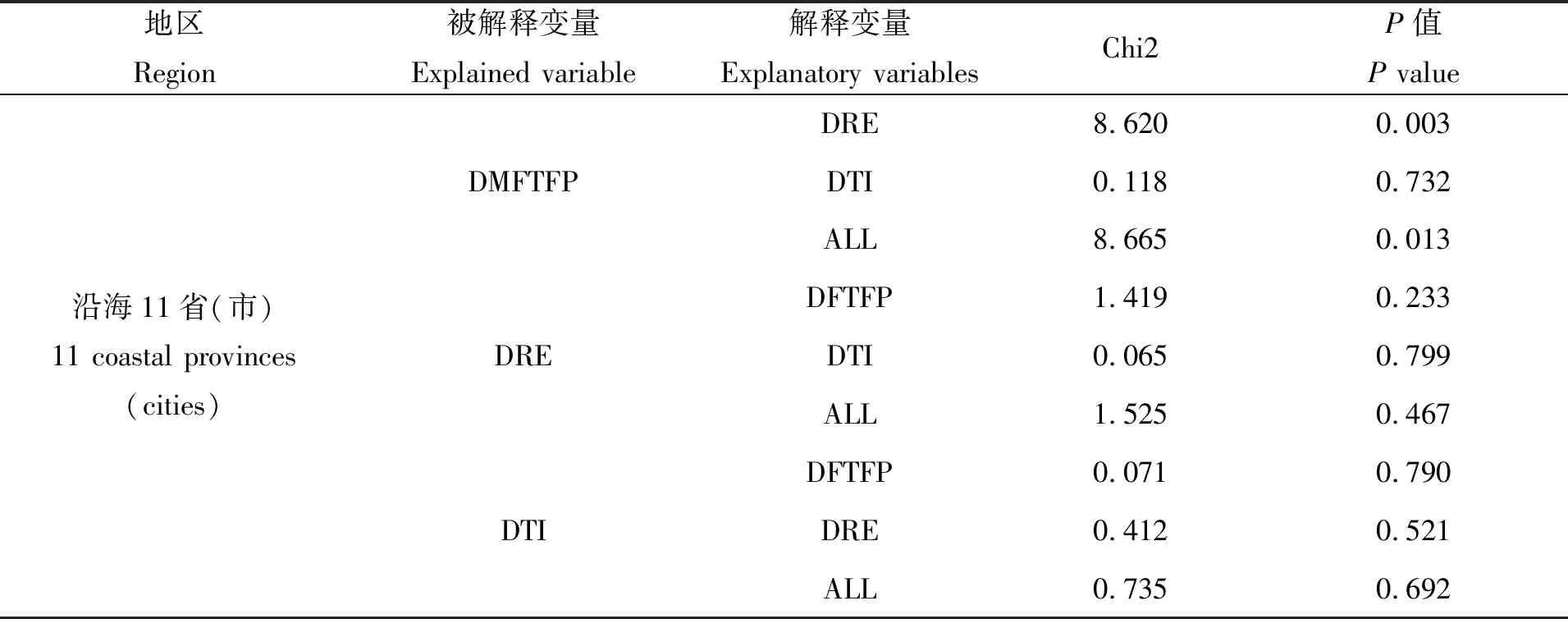
表6 格兰杰因果检验结果

续表6

2.5 脉冲响应函数分析

脉冲响应函数(Impulse response function，IRF)是指对某一内生变量施加一个单位脉冲而另一个变量的变化程度，有时也可理解为某个内生变量发生变化时，其对整个模型的影响程度。本文经过200次蒙特卡罗实验，得到沿海11省(市)、黄渤海地区、长三角地区和珠三角地区的脉冲响应函数图。其中每幅图的纵坐标代表变量受到的冲击，横坐标代表冲击时间。而每幅图的第一列都代表当科技创新受到一个标准差大小的冲击时，科技创新、环境规制和海洋渔业全要素生产率做出的反应；第二列表示当环境规制受到一个标准差大小的冲击时，科技创新、环境规制和海洋渔业全要素生产率做出的反应；第三列表示当海洋渔业全要素生产率受到一个标准差大小的冲击时，科技创新、环境规制和海洋渔业全要素生产率做出的反应。从图1至图4可知，全部变量的脉冲响应函数经过10期后，值都趋于0，呈收敛趋势，说明本文采用的PVAR模型是稳健的。

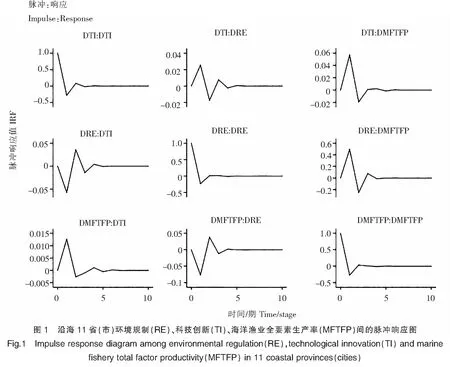
1)沿海11省(市)脉冲响应函数分析

如图1所示，当科技创新受到一个正向单位冲击时(第一列)，科技创新自身、海洋渔业全要素生产率大体呈正向驱动，环境规制呈波动状态，但整体上表现出正向影响，说明科技创新能够推动自身的发展及海洋渔业全要素生产率的提高，但对环境规制的发展在短期内很难推动。当环境规制受到一个正向单位冲击时(第二列)，环境规制、海洋渔业全要素生产率整体表现出正向影响，且从第4期开始都趋于稳定，说明环境规制对其自身和海洋渔业全要素生产率具有很强的促进作用，科技创新则反之。当海洋渔业全要素生产率受到一个正向单位冲击时(第三列)，除海洋渔业全要素生产率自身呈正向驱动外，科技创新和环境规制的波动趋势一致，且正向影响居多，表明海洋渔业全要素生产率在短期内可以促进科技创新和环境规制的发展。

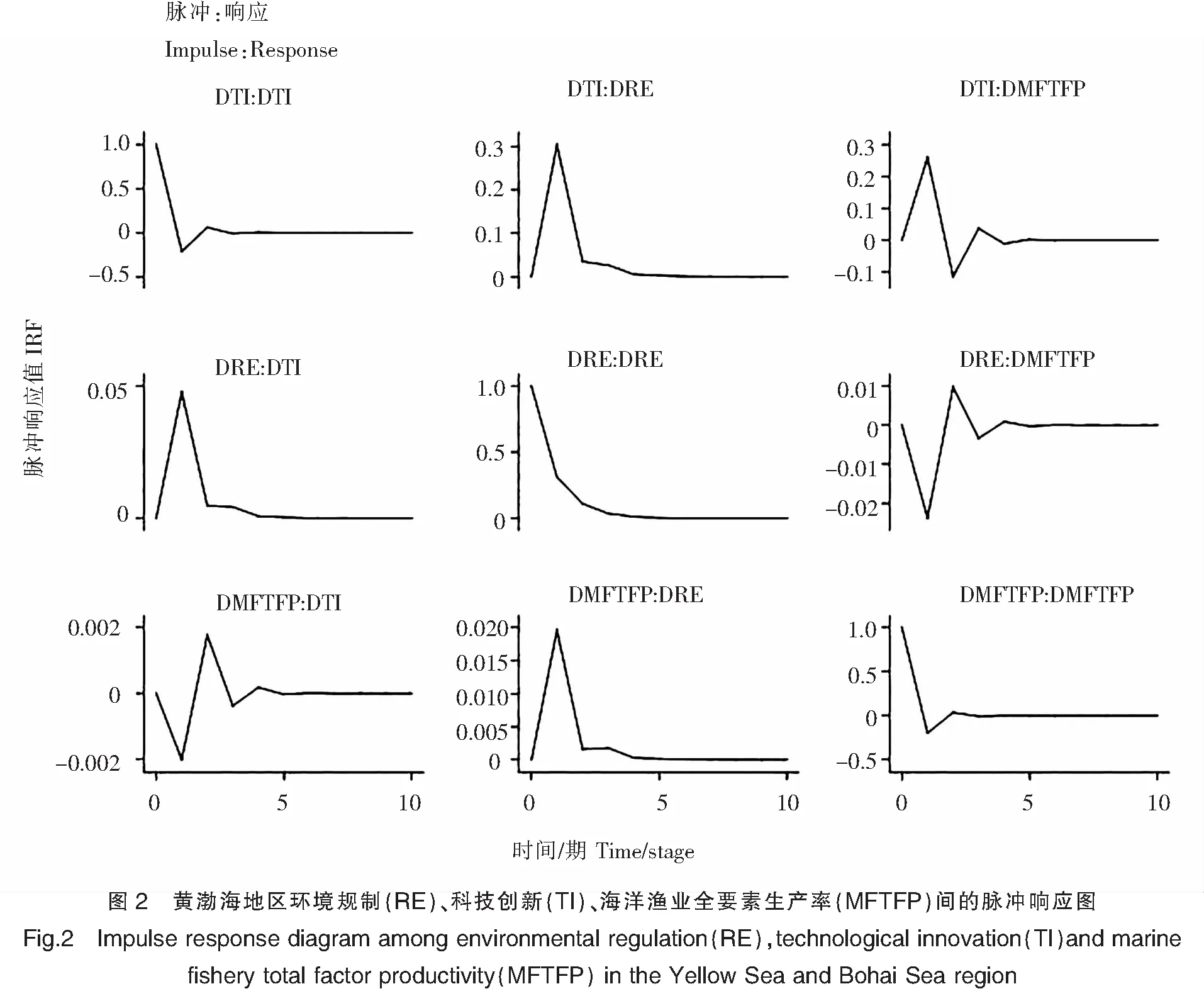
2)黄渤海地区脉冲响应函数分析

由图2可知，当科技创新受到一个正向单位冲击时，科技创新、环境规制、海洋渔业全要素生产率整体均呈正向上升，且从第3期开始趋于稳定，表明科技创新可以持续推动自身、环境规制和海洋渔业全要素生产率的发展；当环境规制受到一个正向单位冲击时，自身和其他两个变量呈现作用与第一列完全一致，且科技创新和海洋渔业全要素生产率在第2期时就达到正向顶峰，由此可知，环境规制对科技创新和海洋渔业全要素生产率具有很强的促进作用，对其自身的促进作用从开始的强逐渐变弱、最后趋于稳定；当海洋渔业全要素生产率受到一个正向单位冲击时，科技创新前两期呈正向影响，随后3～4期呈负向驱动，表明海洋渔业全要素生产率在短期内可以促进科技创新，但后期驱动作用不稳定，环境规制则与科技创新趋势相反，说明海洋渔业全要素生产率在短期内对环境规制具有弱化作用，海洋渔业全要素生产率整体呈正向影响。

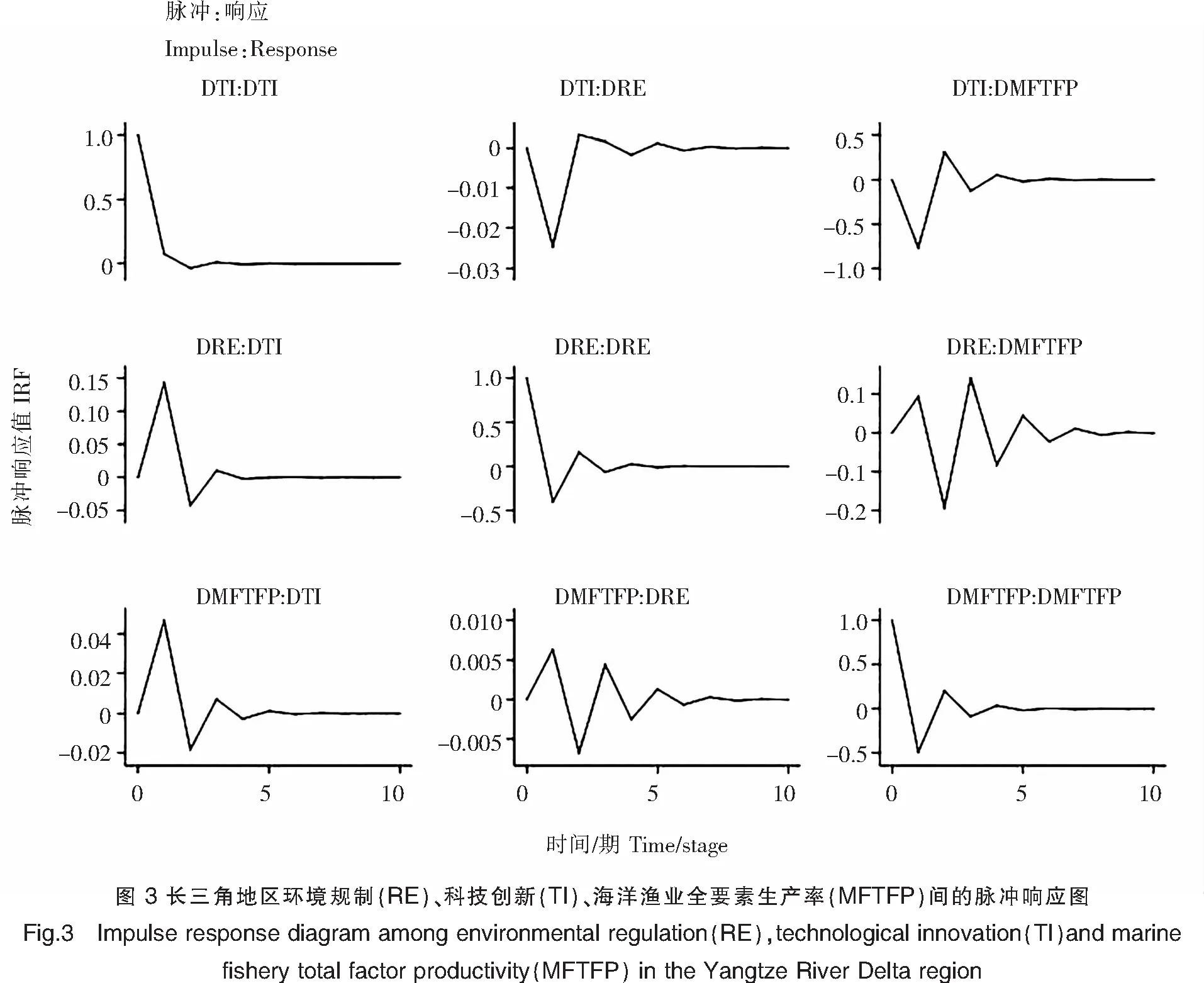
3)长三角地区脉冲响应函数分析

图3呈现了长三角地区环境规制、科技创新、海洋渔业全要素生产率三个变量之间的相互作用结果。首先第一列，当科技创新受到一个正向单位冲击时，科技创新自身的反应均呈正向影响，而环境规制和海洋渔业全要素生产率波动趋势一致，正向影响和负向影响交错分布，且正向影响居多，因此认为科技创新能够促进自身、环境规制和海洋渔业全要素生产率的提高；其次第二列，当环境规制受到一个正向单位冲击时，环境规制自身和科技创新均表现出比较大的负向反应，即环境规制不能推动自身和科技创新的发展，而海洋渔业全要素生产率表现为正负波动，且正向居多、纵坐标的正向值均在0.005水平下，表明环境规制对海洋渔业全要素生产率的提高具有很强的推动作用；最后第三列，当海洋渔业全要素生产率受到一个正向单位冲击时，科技创新和渔业全要素生产率的波动趋势一致，从第2期开始表现为正向影响，而环境规制时正时负，波动幅度较大，且在第8～9期之后才趋于稳定。

4)珠三角地区脉冲响应函数分析

由图4可知，对科技创新施加一个单位脉冲，其自身呈正向作用，环境规划和海洋渔业全要素生产率的响应趋势一致，且在第2期的时候正向作用最大化，第5期开始二者趋于平稳，说明科技创新在短期内对其自身、环境规制和海洋渔业全要素生产率具有负向影响，但这种影响只持续到第2期；对环境规制施加一个单位脉冲，科技创新、环境规制和海洋渔业全要素生产率从最开始的负向转为第3期的正向，最后波动幅度之间缩小，表明环境规制能够促进科技创新、海洋渔业全要素生产率及其自身的发展；当海洋渔业全要素生产率受到一个正向单位冲击时，虽然三个变量的反应大致相同，但环境规制和海洋渔业全要素生产率大多是正向驱动，而科技创新波动浮动较大，前期表现为负向驱动，且在第2期达到负向顶峰。

2.6 方差分解

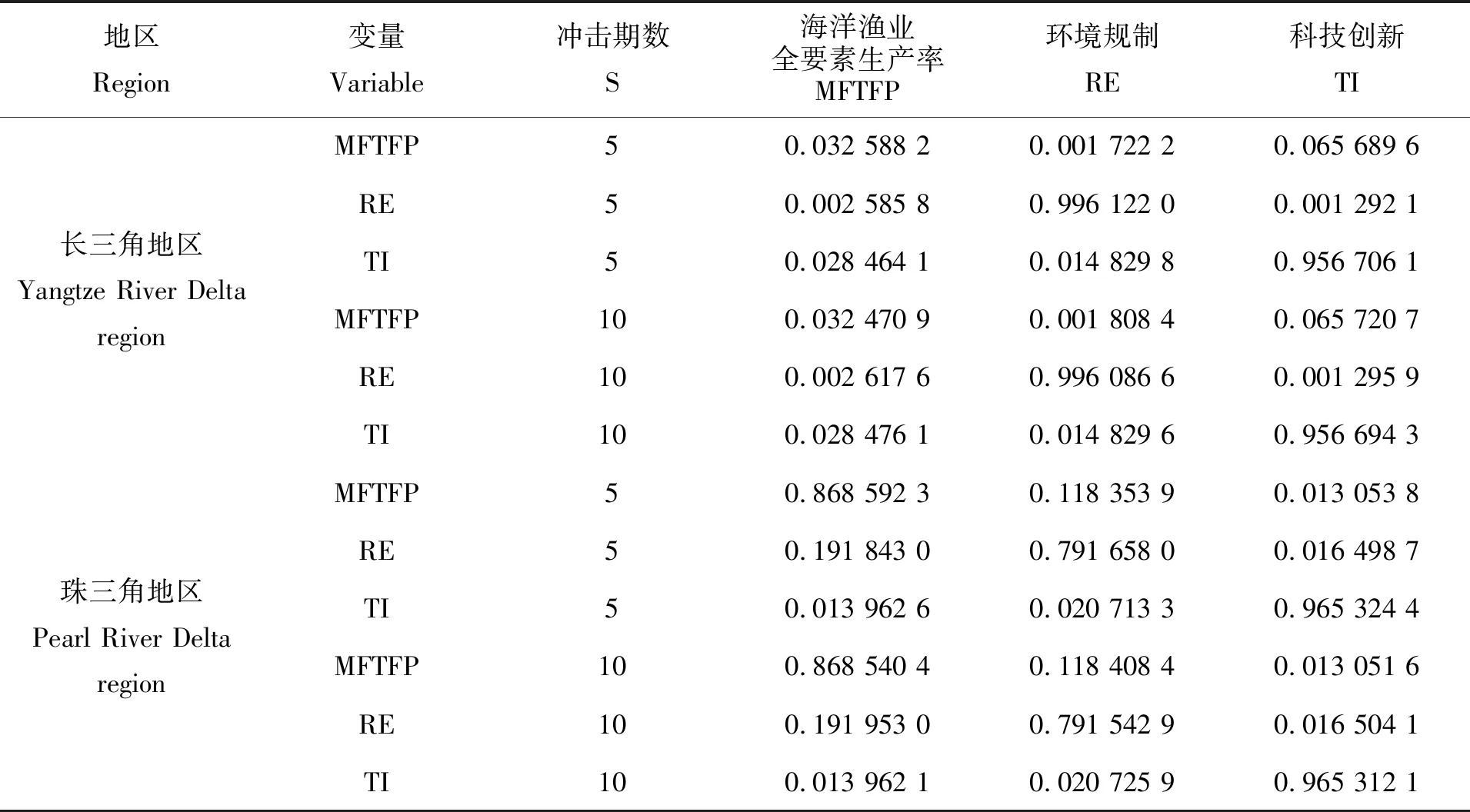
方差分解与脉冲响应基本类似，唯一的不同就是在分析每个内生变量对自身影响的基础上，方差分解分析了各内生变量的不同变动情况对整个模型影响的重要程度。表7分别展现了沿海11省(市)、黄渤海地区、长三角地区和珠三角地区PVAR模型的第5期和第10期方差分解结果，表中海洋渔业全要素生产率、环境规制、科技创新的数据结果分别代表其对第二列变量的预测方差贡献度。

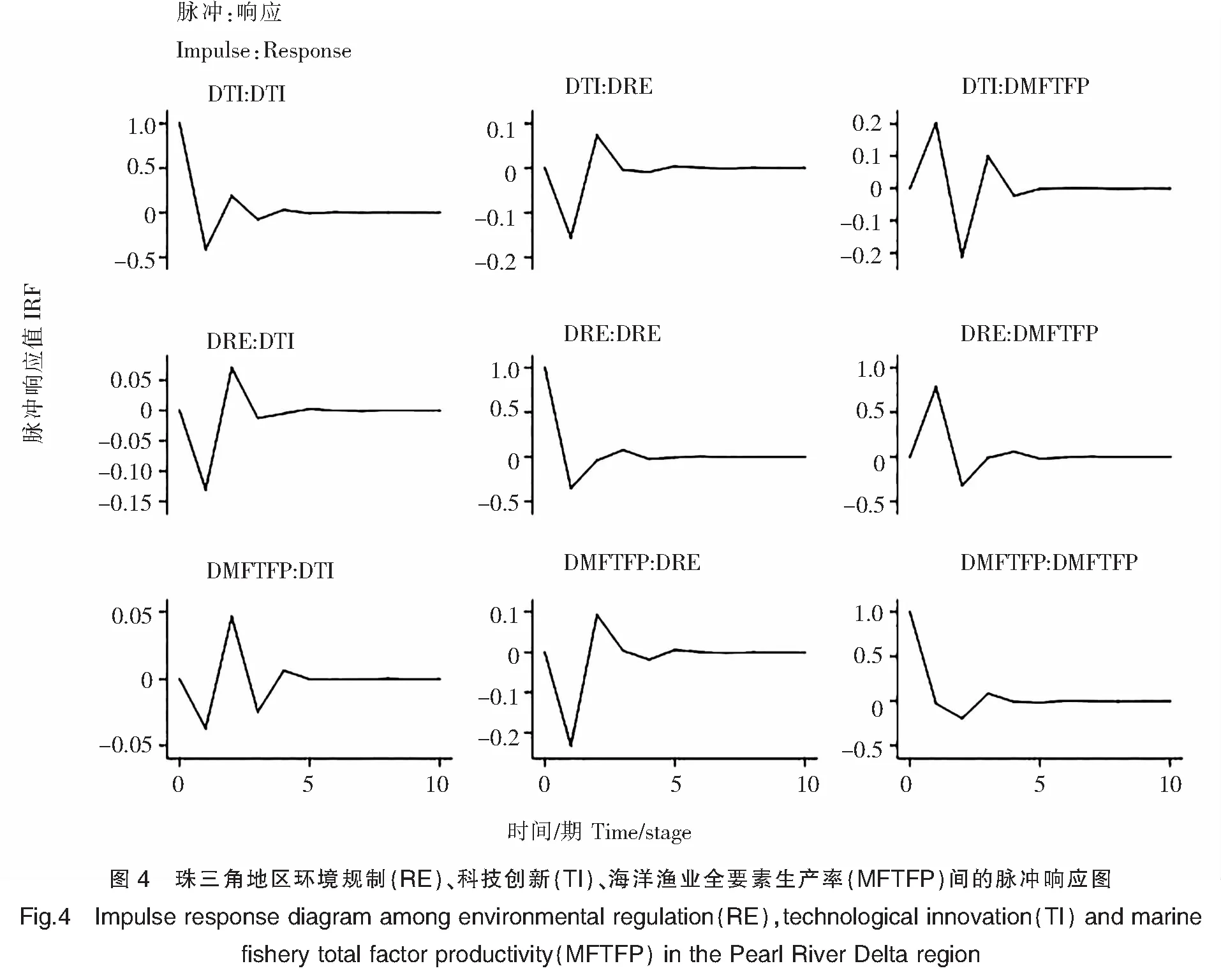
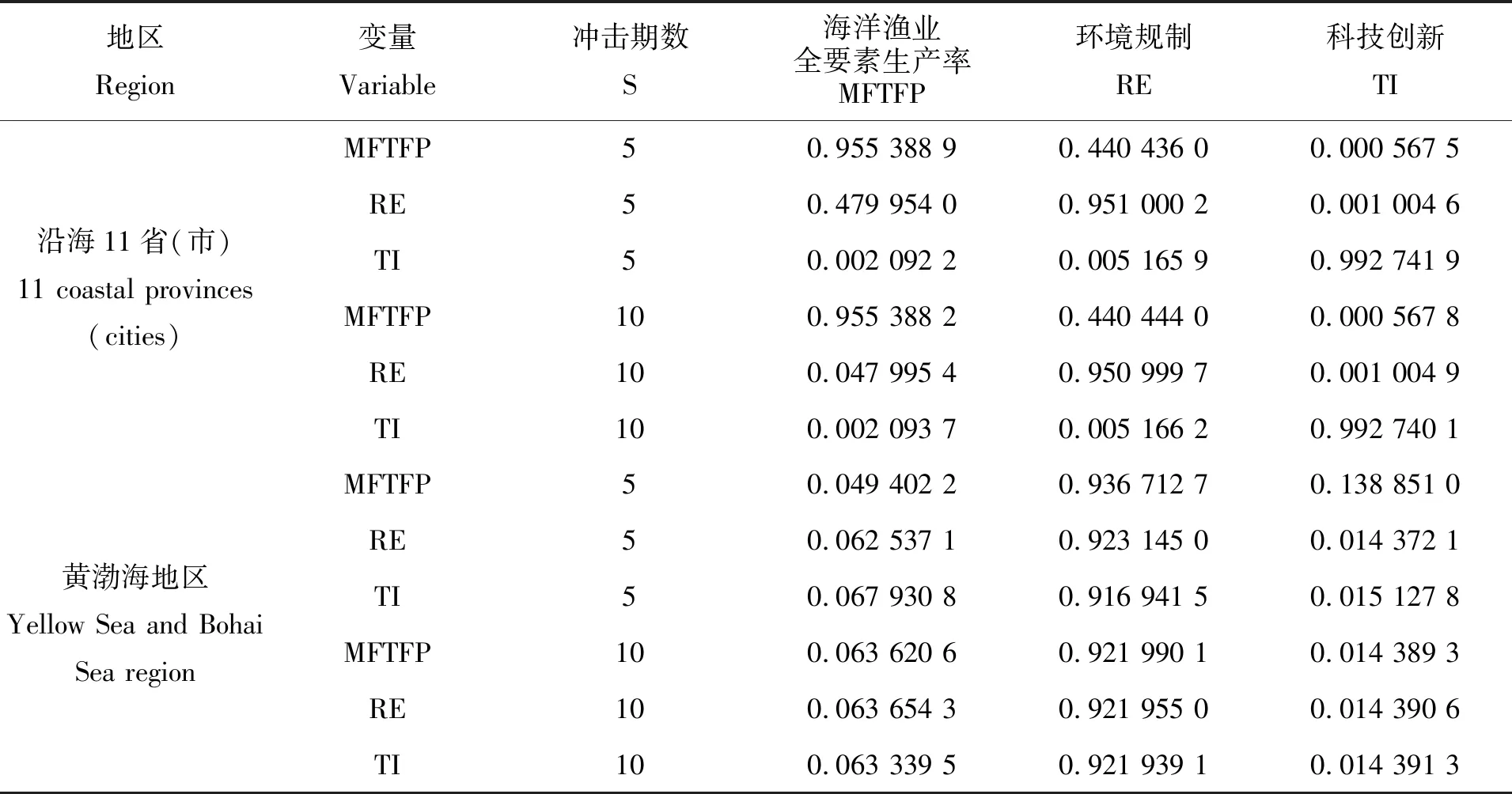
表7 PVAR模型的方差分解结果

续表7

注：表中的“S”代表方差分解中的预测期。

Note：S in the table represented the prediction period in variance decomposition.

由表7可知，1)沿海11省(市)、黄渤海地区、长三角地区和珠三角地区第5期和第10期的方差分解结果大体相同，说明内生变量对其他变量的贡献度从第5期开始趋向稳定，且持续时间长；2)在海洋渔业全要素生产率的贡献程度变动中，沿海11省(市)和珠三角相似，均对自身和环境规制的影响更大，这表明这两个地区的海洋渔业全要素生产率对其自身具有很强的依赖性，而且海洋渔业全要素生产率对环境规制的贡献度大于其对科技创新的贡献度，就黄渤海和长三角来说，黄渤海地区环境规制和科技创新的提高、长三角地区的海洋渔业全要素生产率和科技创新的提高都是由于海洋渔业全要素生产率的作用，且对科技创新的贡献度都是最大；3)在环境规制的贡献程度变动中，四个地区的环境规制对自身的贡献度最大，且都在70%～90%之间，有些甚至超过了90%，这表明沿海11省(市)、黄渤海地区、长三角地区和珠三角地区环境规制程度的大小更依赖于自身的作用，而对海洋渔业全要素生产率的贡献度排名第二，说明环境规制程度促进了海洋渔业全要素生产率的提高；4)在科技创新的贡献程度变动中，与海洋渔业全要素生产率和环境规制的贡献度相同，都对自身具有很大的贡献，环境规制居后，海洋渔业全要素生产率次之；5)从地区来看，沿海11省(市)、黄渤海地区、珠三角地区环境规制对海洋渔业全要素生产率的贡献度均大于科技创新对海洋渔业全要素生产率的贡献度，而长三角地区反之，主要是因为长三角作为我国高经济水平地区，海港贸易发达，较易引进先进的技术，从而创新水平相对较高。

3 结论

整体上，环境规制和科技创新促进海洋渔业全要素生产率的提高，但海洋渔业全要素生产率受环境规制和科技创新的影响存在着明显的区域差异，沿海11省(市)、黄渤海地区、珠三角地区环境规制对海洋渔业全要素生产率的贡献度均大于科技创新对海洋渔业全要素生产率的贡献度，而长三角反之。这表明当前我国在环境规制和科技创新方面的发展存在区域不平衡现象，且长三角地区科技水平明显高于珠三角和黄渤海地区。同样地，海洋渔业全要素生产率对环境规制和科技创新的作用也因不同地区的实际情况而不同，表现出的影响也不同，对于整个沿海地区，海洋渔业全要素生产率在短期内可以推动二者的发展，珠三角地区则反之；海洋渔业全要素生产率对二者的正向影响不显著，但存在一定的潜伏期，在黄渤海和长三角地区，海洋渔业全要素生产率促进科技创新的发展，短期内对环境没有推动作用。再具体到环境规制和科技创新二者，不论是格兰杰因果还是GMM估计、脉冲响应，对“环境规制对科技创新是促进还是抑制？”“科技创新对环境规制是促进还是抑制？”这类问题都很难作出判断，由此可认为环境规制与科技创新的相互作用不对等。

根据PVAR模型的实证结果，环境规制和科技创新对海洋渔业全要素生产率的发展均有促进作用，因此需要通过相关举措来加强环境规制、革新技术，进而推动海洋渔业绿色可持续发展。对于环境规制来说，针对沿海不同省市环境规章作适当补充和调整，加强对渔业环境的监管力度，严格控制排放，做到“源头治理”。如由“长三角地区环境规制对海洋渔业全要素生产率的贡献大于科技创新对生态效率的贡献”可建议，通过规范长三角地区相关环境保护标准，划分环境污染程度，并对污染海洋环境的个人和企业实施相应的处罚，而且严重的将追究刑事责任，以实现环境的优化。再者，鼓励当地政府出台有关保护渔业的政策措施，成立专门的渔业环境监督管理局，借助媒体平台向大众普及渔业环保知识，间接提高公民的环保意识。对于科技创新，珠三角、黄渤海两大地区应首先学习借鉴长三角渔业发展的技术，加强地区间的技术联动；其次完善科技创新机制，不仅要提高福利待遇，引进科技人才，还需培养多元化、专业性强的渔业技术人才，实现高校、企业和科研团队的三重联动，进而推进科技成果的转换；最后要实施科研奖励机制，对在促进渔业发展方面有重大贡献的人、团队要予以奖励和表彰，鼓励渔业科技研究，以上二者综合均衡发展，共同引领渔业绿色健康可持续发展。