新疆工作效果预测评价分析——以新疆旅游业为例

闫海波, 殷生杰

(新疆财经大学 统计与数据科学学院，新疆 乌鲁木齐 830013)

0 引 言

当前，新疆呈现出大局稳定、形势可控、趋势向好的态势，以社会稳定和长治久安为总目标的治疆方略已取得了显著成效。“十三五”时期，新疆提出将旅游业打造成战略支柱产业和稳疆富民产业，随着旅游兴疆战略的不断推进，旅游业呈现出“井喷式”增长，截至2019年，新疆旅游业全年接待旅游人数突破2.1亿人次，增长率超过40%。灰色模型一经提出就被广泛应用于经济、管理、农业、医学、社会发展等各个领域，该模型主要针对具有小样本、贫信息特征,以及富有不确定性的研究对象，经过对这些数据的生成和开发,发现其中有价值的信息,并对系统的运行和演化规律作出准确有效的描述。在新疆旅游业发展研究中，吴科峰[1]、孙盼盼等[2]、李啸虎等[3]分别从行业现状、波动周期和发展趋势方面展开相关研究。在灰色模型运用方面，邱亚利[4]、刘红梅等[5]对不同地区旅游景点的游客数及客源进行了预测分析，严胡勇[6]、朱登远等[7]指出灰色模型在小样本数据中短期预测上优于其他模型。各个领域中灰色模型均表现出较好的拟合效果和预测精度，为解决实际问题提供了可靠模型；但鲜少有人运用灰色模型从政策实施效果评价角度分析量化政策施行是否达到了预期成效。综上所述，新的发展常态需要新的评价体系，以旅游业为切入点对新疆工作的实施效果进行评价就颇具研究意义。文中以接待游客总数为研究对象，运用传统灰色GM(1,1)模型和优化灰色GM(1,1)模型进行建模,研究新疆工作的实施效果，并量化分析新疆工作的实行对新疆旅游业及经济发展的影响。

1 研究方法

目前，研究GM(1,1)模型的主要目标是拓宽适用范围、提高预测精度和构建一个数学性质良好的模型[8-9]。实际上，在建模过程中，变量越多的模型，预测精度往往越高。如果把序列累加阶数、模型初始值和背景值都看作变量，优化的变量越多，得到的模型精度越高。近年来，许多学者都从改变灰色模型基本结构的角度出发，尝试提高模型的预测精度[10-13]；仅有少数学者从生成系数的背景值优化出发，对模型的参数估计进行改进[14-19]。不管是修正模型结构，还是优化模型背景值都可以在一定程度上提高模型精度；但预测误差主要来自于对模型背景值的近似。文中尝试运用传统灰色GM(1,1)模型和生成系数为不等权常数的GM(1,1)模型对旅游数据进行建模。

1.1 传统灰色GM(1,1)模型

首先建立基本的灰色预测模型GM(1,1)

(1)

式中:x(1)——一次累加生成数列;

t——时间;

a,u——待估参数，分别称为发展灰数以及内生控制灰数。

在此需要建立一次累加生成数列。设原始数列为

x(0)(t)={x(0)(1),x(0)(2),…,x(0)(n)},

(2)

按照如下方式进行一次累加，能够得到生成数列(n为样本空间)

(3)

以最小二乘法求其参数a,u。设

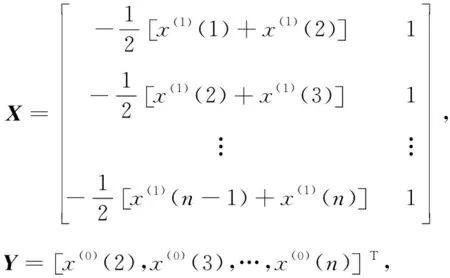
(4)

参数识别a,u,

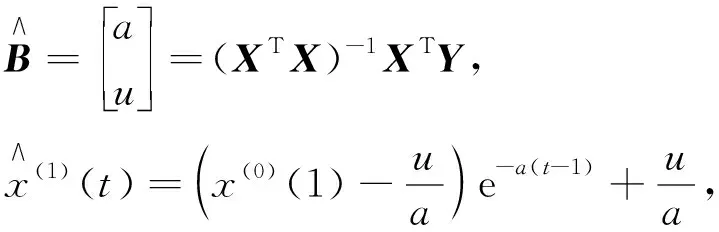
(5)

进而由

(6)

得原始序列的预测值。

1.2 生成系数为不等权常数的GM(1,1)模型

首先建立基本的灰色预测模型GM(1，1)(见式(1))，在此需要建立一次累加生成数列,设原始数列为式(2)，按照式(3)进行一次累加，能够得到生成数列(n为样本空间)，以最小二乘法求其参数a,u。设

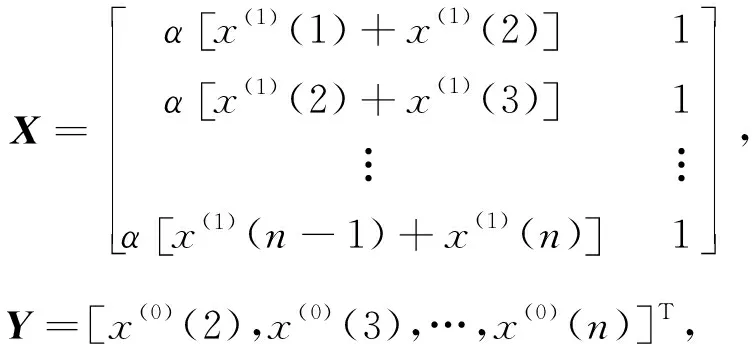
(7)

参数识别a,u(见式(5)),进而由式(6)得原始序列的预测值。

为提高模拟和预测精度，对α可在[0,1]上均匀地选取100个值，选择使

达到最小值的α。

1.3 检验预测值

为判断灰色预测模型的可行性，采用残差检验和级比偏差值检验对模型预测精度进行分级。

1.3.1 残差检验

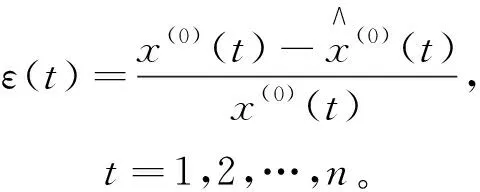
(8)

1.3.2 级比偏差值检验

(9)

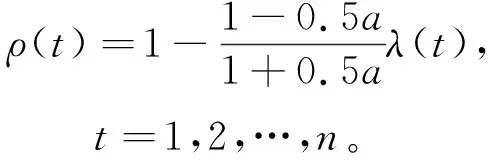
(10)

1.4 评价体系

1.4.1 预测精度等级划分

根据以往经验将模型预测精度划分为高(|ε(t)|,|ρ(t)|∈(0,0.1))、一般(|ε(t)|,|ρ(t)|∈(0.1,0.2))和低(|ε(t)|,|ρ(t)|∈(0.2,∞))三个等级。

1.4.2 预测预报

检验合格后，选择拟合效果较好的模型对接下来几年的数据做出预测，

…

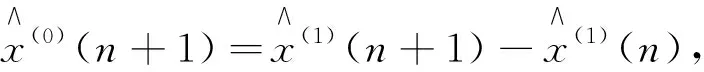
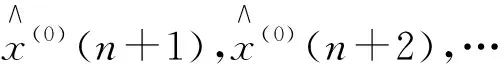
1.4.3 政策实施效果评价

在对政策实施效果进行评价时，根据预测精度等级划分表引入政策评价体系，将政策实施效果分为：一般(|ε(t)|,|ρ(t)|∈(0,0.1))，良(|ε(t)|,|ρ(t)|∈(0.1,0.2))，优(|ε(t)|,|ρ(t)|∈(0.2,∞))三个等级，而预测值和真实值之间的绝对残差则是政策实施效果的具体表现。因此，对新疆工作措施效果的评价则不仅仅拘泥于简单的等级划分，而是以具体数字的形式量化得出，这将会对相关政府机构的后续工作有重要的指导意义。

2 数据说明

新疆GDP和接待游客总数之间都有相同的增长趋势,如图1所示。

图1 新疆GDP和接待游客总数趋势图

2000-2019年，除2009年及2014年由于特殊原因下降较为明显以外，其它年份均呈现出上升趋势。综上所述，以旅游业为切入点研究新疆工作总目标有一定的现实意义。

由于灰色预测模型需要假设所有影响因素都是随机的，经过对数据的进一步分析不难看出，新疆GDP和接待游客总数在2009年出现了违背其总体发展趋势的数值，众所周知,2009年数据出现骤减有其特殊原因。首先，为排除这一因素的干扰，需着眼于2010-2019年数据，其次，灰色模型在短期预测具有较好的预测效果，2010年到“十三五”计划提出之际已有6 a；采用这样的数据集符合文中研究目的。所以，文中选取的数据为新疆2010-2019年接待游客总数(万人次)，见表1。

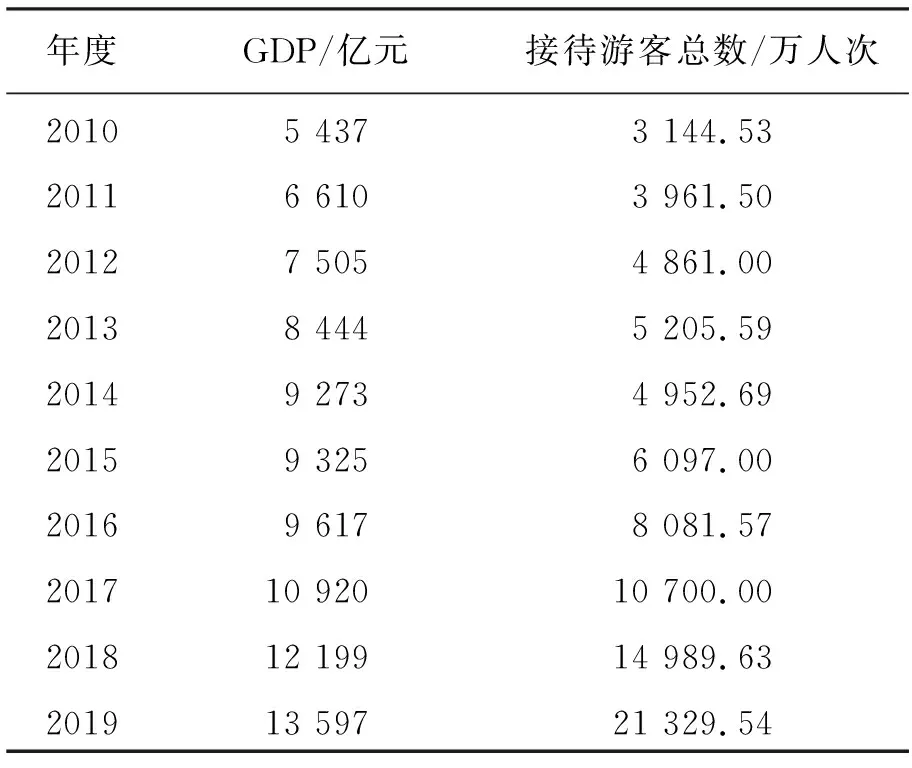
表1 新疆2010-2019年旅游数据

3 实证结果分析

文中以2010-2015年接待游客总数为样本内数据，建立传统灰色GM(1,1)模型和生成系数为不等权常数的优化灰色GM(1,1)模型进行拟合，选择通过各项检验且拟合效果最优的模型对2016-2019年数据做出预测，最终以达到对政策实施效果进行评价及量化分析的目的。

对接待游客总数建立传统灰色GM(1,1)模型，即背景值函数为

x(1)(t)=0.5x(1)(t-1)+0.5x(1)(t),

计算得出其参数估计值：a=-0.086 7,u=3 731.988 9。

时间响应方程为

46 207.4e0.086 7(t-1)-43 062.8。

由式(8)计算出预测值的相对残差，由式(10)计算得出级比偏差，相关结果见表2。

表2 接待游客总数灰色预测结果

根据上文MAPE公式计算MAPE=5.74%。

对接待游客总数建立生成系数为不等权常数GM(1,1)模型，即背景值函数为

x(1)(t)=αx(1)(t-1)+(1-α)x(1)(t),

其中，α在0到1以0.01为步长中选取，计算平均绝对百分误差MAPE，并绘制平均绝对百分误差随α变化曲线，如图2所示。

当α=0.25时，MAPE达到最小值,MAPE=5.29%。

计算得出其参数估计值：a=-0.088 1,u=3 821.060 7。

时间响应方程为

46 511.0e0.088 1(t-1)-43 377.0。

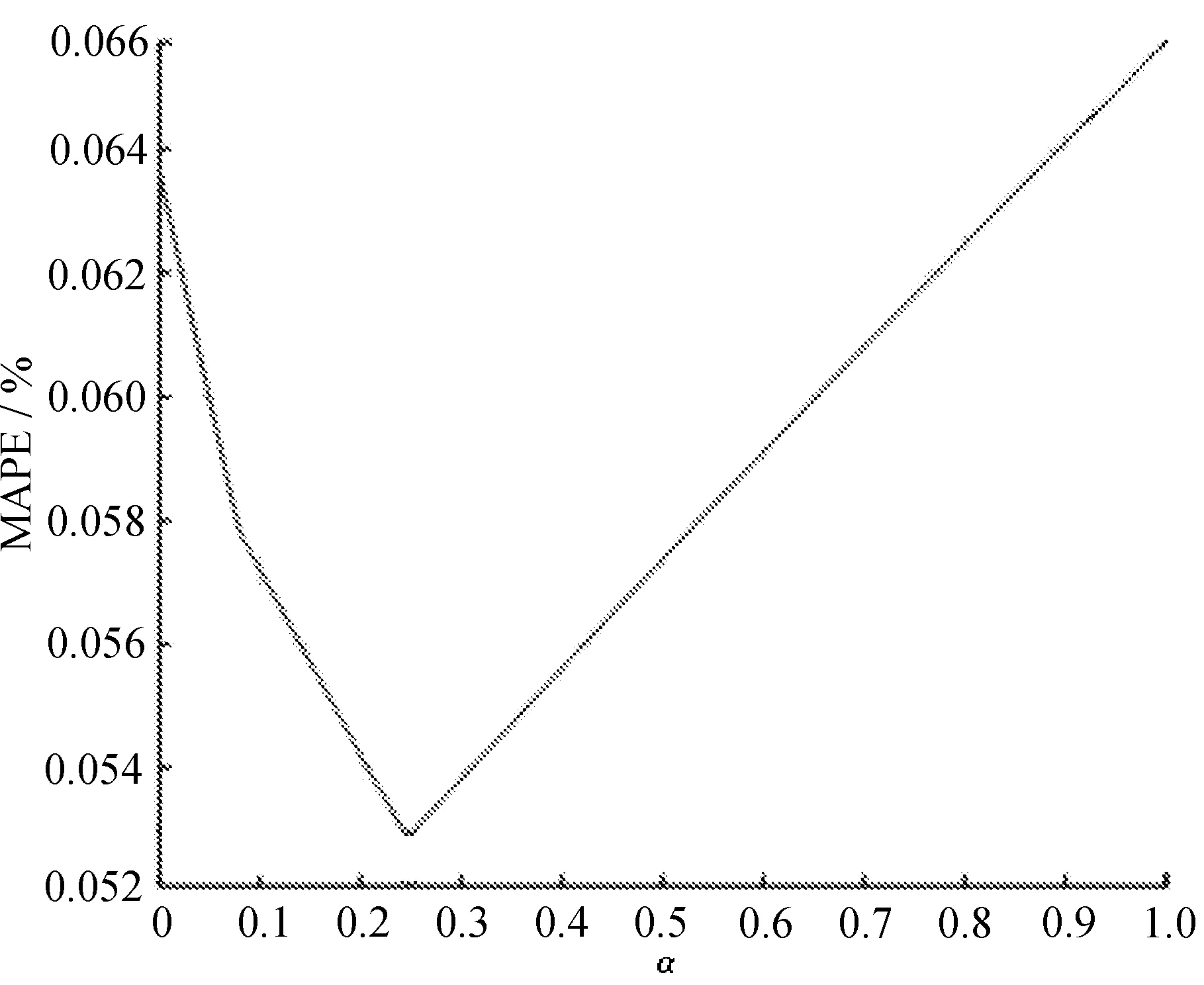
图2 平均绝对百分误差随α变化曲线

根据表2可以得出，在接待游客总数的预测结果中,各年度相对残差均小于0.11，级比偏差均小于0.15，预测精度等级均达到一般或高等级，结果非常理想。对比分析两个模型的MAPE值可以得出，生成系数为不等权常数的优化灰色GM(1,1)模型的平均绝对百分误差较小，即拟合结果优于传统GM(1,1)模型。现将该模型用于对2016-2019年接待游客总数进行合理外推,并对预测结果做相应的检验，详见表3。

表3 2016-2019年接待游客总数灰色预测结果及政策实施效果

根据生成系数为不等权常数灰色GM(1,1)模型对2016-2019年接待游客总数的预测结果看，各年相对残差均大于0.25，政策实施效果均为优；级比偏差也均大于0.18，政策实施效果均为良及以上。综合上述两个指标，新疆工作总目标措施实施效果良好。2016-2019年实际数据与预测值之间的差距分别为1 629.74、3 663.80、7 316.66和1 2961.95，也就是说,新疆工作总目标各项措施实施带来的红利逐年递增。接待游客总数实际值与预测模型之间的关系如图3所示。

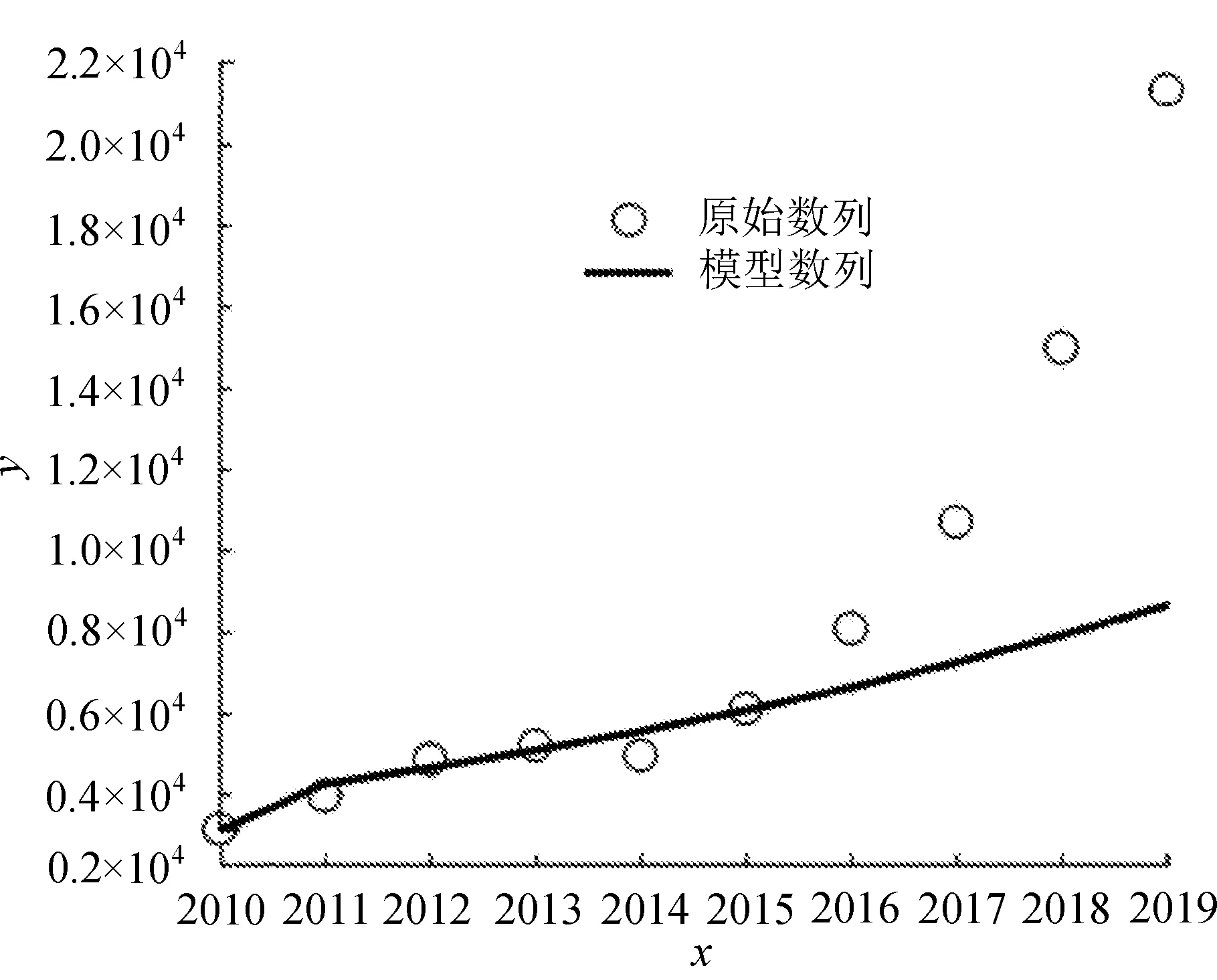
图3 接待游客总数实际值与预测模型之间的关系

2010-2015年，除了2014年其他数据均在模型预测值附近，但这也符合2014年特殊情况对该年的严重影响；2016-2019年的预测数据同实际数据之间存在明显差距，也就是说,自2014年第二次中央新疆工作座谈会和自治区第十二届人大四次会议以来，新疆工作成效非常显著，党中央稳疆建疆的措施在各级相关部门的努力奋斗和积极参与下起到了越来越好的效果。

4 结 语

首先以新疆旅游业发展为切入点,对2010-2015年新疆旅游接待游客总数统计数据构建传统灰色GM(1,1)模型和生成系数为不等权常数灰色GM(1,1)模型,深入研究新疆工作的实施效果。在预测精度方面，传统灰色GM(1,1)模型和生成系数为不等权常数灰色GM(1,1)模型的拟合精度均达到建模要求，且生成系数为不等权常数灰色GM(1,1)模型的平均绝对百分误差优于传统GM(1,1)模型。然后利用生成系数为不等权常数灰色GM(1,1)模型对2016-2019年接待游客总数进行预测，最后通过相对误差值和级比偏差值对新疆工作的实施效果进行评价，并利用预测数据与真实值之间的差异，量化新疆工作的具体成效。结果表明，新疆工作实施效果优良，旅游业所呈现出的“井喷式”发展表明新疆近年来社会稳定、治安良好，以社会稳定和长治久安为核心的新疆工作成效显著。