基于模型平均方法的糖尿病病人生存时间预测研究

程云飞，王淑影，张亚男

(长春工业大学 数学与统计学院，吉林 长春 130012)

0 引 言

糖尿病是一种常见的内分泌代谢性疾病，国际糖尿病联盟在Diabetes Atlas上预测糖尿病患者数量将持续升高。糖尿病在中国是高发疾病，常伴有家族遗传史，长期血糖控制不良将导致多种急性、慢性疾病并发，使人体抵抗力变差，危及患者生命。由于无法根治，糖尿病的病症只有及早发现、及早治疗才能降低出现并发症的隐患。因此，构建糖尿病病人的生存时间预测模型，对提高糖尿病病人的生存质量有着重要意义。

在实际研究中，针对某一领域的一个问题，通常可以建立多个模型，如何在所有可能的模型中选择适合的模型是统计学界研究的核心问题之一。模型选择的目标是从模型集合中选出估计或预测误差较小的模型，如Akaike Information Criterion (AIC)、Bayes Information Criterion (BIC)、Focused Information Criterion (FIC)等。模型选择方法在一定程度上解决了选择较“优”模型的问题，然而模型选择过程中总是存在着不确定性，因此无法避免选择很“差”模型的风险。对于模型选择过程中存在的缺点，学者们进行了大量研究，近些年来，模型平均方法作为解决模型选择不确定性的重要方法受到了广泛关注。与模型选择方法相比，模型平均方法的估计及预测并不依靠于单个模型，而是基于整个候选模型。Bates J等[1]将模型组合用于对航空需求的预测，研究肯定了组合预测的优势。目前，按照权重形式的不同，模型平均方法可以分为两大类，分别为贝叶斯模型平均和频率模型平均。最初的模型平均方法可以追溯到由Buckland S T等[2]提出的基于AIC和BIC两种信息准则的Smoothed-AIC(S-AIC)和Smoothed-BIC(S-BIC)方法，它们也是最简便、常用的方法。对于小样本量的研究，Hua Liang[3]提出的OPT权重选择方法具有良好的表现。张新雨等[4]介绍了几种常用的模型平均方法，并将它们应用于中国粮食产量预测，且取得了较好的预测效果。朱容等[5]将模型平均方法应用于部分函数线性模型，并对肉类和玉米样本的近红外反射光谱数据集进行分析，结果表明,模型平均方法要比模型选择方法的预测效果更好。

综合以上国内外文献可以发现，模型平均方法提高了估计及预测的稳健性，为选择模型提供了一种保障机制，降低了选择很“差”模型的风险性[6]。在一定情况下，相较于模型选择方法，模型平均方法在解决模型不确定和研究医学方面预测问题上具有一定优势。因此，文中将模型平均方法应用于糖尿病病人的生存时间预测上。

1 基于模型平均方法的估计

文中考虑如下线性模型

(1)

式中：Yi——因变量;

Xi——p维必选协变量向量;

Zi——q维可选协变量向量;

β——p维回归参数;

γ——q维回归参数;

εi——随机误差项。

因此,模型中的待估参数为θ=(β′,γ′)′。

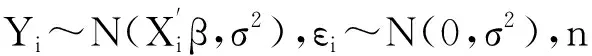
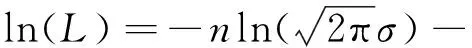
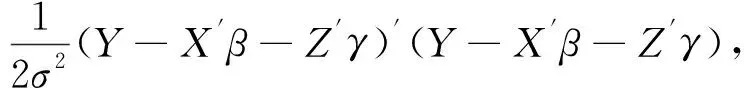
(2)

对其求极大值，参数的最大似然估计为

在医学研究中，影响疾病预后生存时间的协变量往往有多个，将不同的协变量组合就能得到不同的模型，但在不同的模型里如何选择出最优模型是我们关注的重点。权衡模型复杂度与优良性的标准，简称AIC；贝叶斯信息准则，简称BIC。两者都是基于模型的信息量来遴选最优模型，这两种最常用的信息准则定义为

HIC=-2logl+F,

(3)

式中：HIC——表示AIC或者BIC；

l——模型的极大似然函数；

F——惩罚项。

当F=2g时，式(3)为AIC表达式，当F=glog(n)时，式(3)为BIC表达式，其中g为未知参数个数，n为样本个数。

通常情况下，多元回归模型通过拟合因变量与多个协变量估计模型中的参数，单一模型选择的过程中总是存在着不确定性，选择的模型过于复杂或是过于简单都会使得估计或者预测的方差偏大[7]。因此统计学家提出模型平均的思想。Buckland S T等[2]介绍了S-AIC和S-BIC两种基于信息准则的组合权重方法，则组合权重为

(4)

式中：k——第k个模型；

K——模型集合中模型的数量；

HIC——表示AIC或BIC；

ωk——第k个模型所对应的权重。

假定X中有m1个必选协变量，Z中有m2个可选择的协变量，因此模型集合中有N=2m2个子模型可供选择。在实际研究中，某些模型不符合实际可以事先排除，所以至多考虑N≤2m2个子模型。首先假定OPT方法的权重形式，

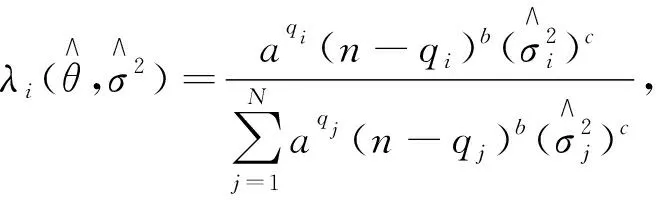
(5)

M=In-X(X′X)-1X′，

因此，全模型下σ2的最小二乘估计为

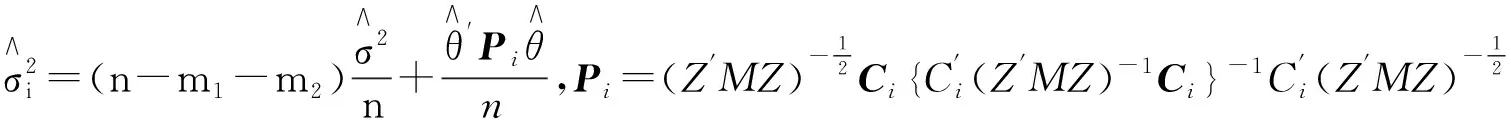
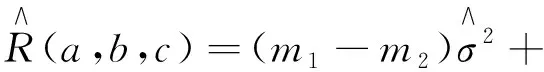
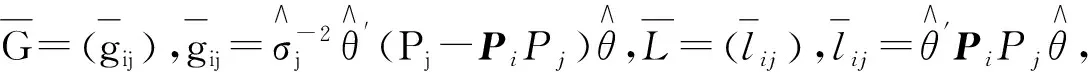
将所有候选模型的估计与上述模型平均方法计算的权重平均起来，可得到Yi均值的组合估计

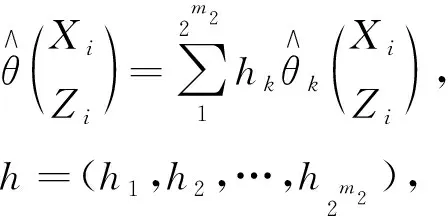
(6)

式中：k——第k个模型；

hk——上述模型平均方法估计的各候选模型估计权重。

2 实证分析

文中选取的数据为1971-1988年对128位糖尿病人随访研究的临床数据，数据来源于Ovid数据库。所选的协变量有X1(患者被诊断出糖尿病时的年龄)、Z1(身体质量指标(BMI))、Z2(心电图读数(ECG))、Z3(舒张压与收缩压之差(DBF-SBF))、Y(自基准检查起的生存时间)。文中将2种模型选择方法AIC、BIC，3种模型平均方法S-AIC、S-BIC、OPT应用到糖尿病数据集上。为了便于分析，对数据做标准化处理。根据以往糖尿病预后因素所做的研究，患者确诊糖尿病时的年龄对自基准检查起的生存时间有着显著影响，故选定X1为必选协变量，其他3个协变量Z1、Z2和Z3为可选协变量，因此模型集合中有N=23=8个备选模型。例如，第1个模型只有必选协变量为Y=β1X1+ε，第2个模型包含可选协变量为Y=β1X1+γ1Z1+ε，以此类推，第8个模型包含必选协变量和所有可选协变量，即全模型为Y=β1X1+γ1Z1+γ2Z2+γ3Z3+ε，根据不同的加权方法将全部模型预测值加权平均，得到最后的预测结果。文中目的是根据试验研究中的协变量数据预测糖尿病病人自基准检查起的生存时间。

结合实例分析比较以上5种方法的预测效果，将糖尿病病人数据分为训练集与测试集，将训练集的样本量设置为n1=90、100、110、120，测试集样本量n-n1，样本量为n=128，使用任意训练集样本进行回归，得到未知参数估计，然后对测试集样本进行预测，这个过程重复c=1 000，则最后得到的均方预测误差(MSPE)为

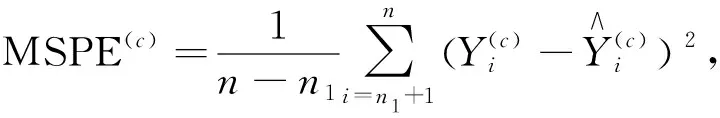
(7)

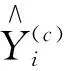
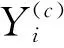
计算5种方法MSPE的均值与中位数，结果见表1。

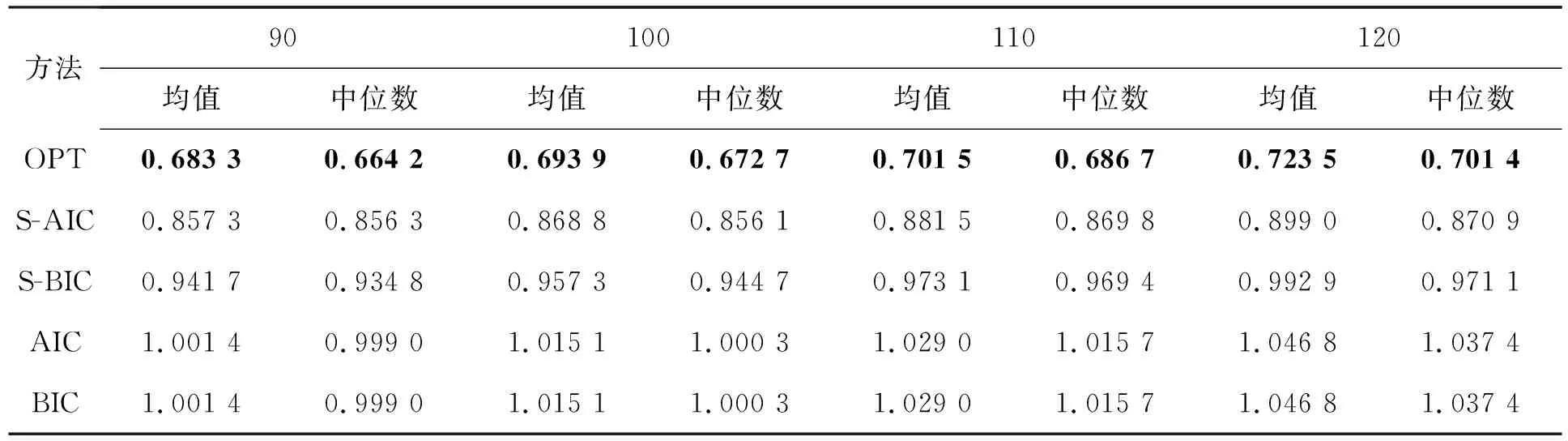
表1 糖尿病病人生存时间的均方预测误差

由表1可以得出，OPT模型平均方法得出预测值的MSPE均值与中位数比其他4种方法要小，说明OPT模型方法均方预测误差较小，预测精度要优于其他4种方法；S-AIC和S-BIC方法MSPE的均值与中位数都要比AIC和BIC方法要小，说明在糖尿病病人生存时间预测研究中，模型平均方法比模型选择方法的预测精度更高。此外，两种模型选择方法的预测结果很接近，而S-AIC要略优于S-BIC方法。

3 结 语

对1971-1988年128位糖尿病病人随访研究的临床数据运用模型平均方法与模型选择方法进行了病人生存时间的预测。通过对比5种方法的MSPE均值与中位数发现，OPT方法的预测精度更高，S-AIC和S-BIC方法要优于AIC和BIC方法。综合比较，在对糖尿病病人的生存时间进行预测时，模型平均方法要优于模型选择方法。

根据文中研究结果可以发现，模型平均方法在糖尿病病人生存时间的预测中取得了较好的效果，因此可以把模型平均方法运用到更多数据类型或模型中，如文中研究的是线性模型，在后期研究中可以将模型平均方法进一步扩展到部分线性模型中。