基于Sin-K2DPCA的三维人脸识别*
2021-12-22福州大学至诚学院吴林
福州大学至诚学院 吴林
针对三维人脸多表情、多姿态变化同时存在,人脸的非刚性部分存在变形且人脸点云数据不同程度缺失的问题,把“角度”的理念引入非线性区间,本文提出基于Sin-K2DPCA三维人脸识别。这样就可以在多数据融合的基础上相互的取长补短,取得更好的识别结果。该研究探索性地将三维点云人脸数据应用于Sin-K2DPCA,并进行识别结果的对比与分析。
0 引言
随着人工智能的高速发展,人脸识别技术广泛应用于众多领域。虽然二维人脸识别技术已经非常成熟,但受光线、年龄、表情、姿态等因素的影响较大。而三维人脸数据具有更好的鲁棒性,更高的防伪性,因此三维人脸识别技术慢慢应用到越来越多的场景中。人脸识别是计算机模式识别中的一个重要领域,其中人脸识别中的特征提取至今仍然是一个重要的课题。本研究提出的人脸识别新算法,将有效提高三维人脸识别的准确度,并降低计算复杂度。
1 国内外研究动态
20世纪90年代初由Turk和Pentland[1]提出了主成分分析(PCA),基本思想是将图像经过K-L变换后由高维向量转换为低维向量,并形成低维线性向量空间,人脸投影到这个低维空间所得到的投影作为识别的特征矢量,所有子空间的正交基就是特征脸。主成分分析(PCA)的不足之处是由于数据量过于庞大且训练样本又相对过少,所以很难精确地评估它的协方差矩阵。为解决这个缺点,杨健[2]等人提出了二维主成分分析(2DPCA)。与传统的PCA不同,2DPCA使用的是二维矩阵,而不是一维向量。也就是说,图像矩阵不需要事先转变成一维向量,与PCA的协方差矩阵相比,使用2DPCA图像的协方差矩阵要小一些。由于PCA算法是一种线性映射方法,它忽略了数据之间高于二阶的统计信息,这在一定程度上影响了识别效果。针对PCA算法的这个缺陷,Scholkopf[3]等人将核方法应用于特征抽取中,提出了核主成分分析(KPCA)。KPCA是线性PCA的非线性扩展算法,它采用非线性的方法抽取主成分,即KPCA是通过映射函数把原始向量映射到高维空间F,然后在F中进行PCA。KPCA对PCA进行了非线性改进,但仍要将人脸图片转换成向量。为解决这一不足,Nat等人[4]提出了非线性的2DPCA(K2DPCA)。K2DPCA还存在以下两个缺点:第一个缺点是当出现异常值时,K2DPCA的鲁棒性仍不够好;第二个缺点是当人脸数据较多时,K2DPCA的核函数数量会成倍增多,这样就增加了计算复杂度和存储空间。为进一步解决这些缺点,Zhou等人[5]提出了基于角度的非线性2DPCA(Sin-K2DPCA)。
使用深度学习的三维点云分类网络在2017年开始出现,Qi等人[6]提出了PointNet深度网络用来达成三维点云数据的切分和分组,解决了点云无序性的问题。虽然创造性地直接将三维点云作为输入的网络,其分类网络取出点云数据的全局特征完成三维点云分组,但是仍存在局部特征丢失的问题;所以,Qi等人[7]又对PointNet网络进行改进,提出了PointNet++的深度网络。在PointNet+分组网络结构中,通过抽样、分类、PointNet三层结构实现从局部特征到全局特征的抽样,使得分类准确度极大提升。2019年,Cai等人[8]在PointNet++网络的基础上结合PointSIFT网络提出了空间聚合网络方法,用多方向卷积的方法采样三维点云空间结构特征,虽然点云分割精度提高了,但是点云分类准确度却比PointNet++分类网络还低。
2 基于Sin-K2DPCA的三维人脸识别
二维人脸识别采用的是二维图片,但是人脸却是三维的,因此采用三维人脸数据进行识别会更加准确。针对三维人脸多姿态、多表情变化共同存在,人脸点云数据会有不同程度缺失,提出了一种分层特征化PointNet++网络[9-10]。其次再把“角度”的理念引入到非线性区域,采用核方法提出了Sin-K2DPCA,并基于F范数度量,把采样数据经非线性运算映射到高维空间后再将重构误差极小化。该研究探索性地将三维点云人脸数据应用于Sin-K2DPCA,并进行识别结果的分析与对比,然后提出一种新的人脸识别算法。
(1)使用了Bagging的随机森林(Random Forest,RF)将初始深度图形中进行脸部区域切割,然后将切割后的脸部初始深度图形转化为点云人脸数据库,再对人脸三维点云进行下取样、翻转和归一化。将归一化后的点云坐标与脸部对应点进行联接,将其作为PointNet++网络的输入。
(2)如图1所示,本研究通过对PointNet网络的MLP添加一个正反馈连接,从而达到对网络结构改进的目的。PointNet++网络可以将不同层次的特征进行多数据融合,实现了不同层次特征的有效利用。在没有增加训练时间的情形下,能够更加有效的传递特征,并使网络训练的计算量降低。
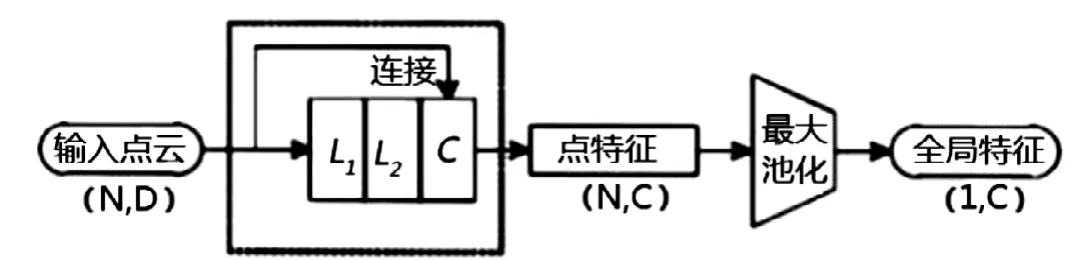
图1 PointNet++网络结构Fig.1 PointNet++network structure
(3)将拼接后的低维特征坐标数据,应用于Sin-K2DPCA进行Matalab仿真,验证利用拼接特征进行识别时特征比对时间是否快于已有人脸识别算法,在CASIA数据集中的平均识别率是否高于已有人脸识别算法。
3 实验结果及分析
3.1 算法识别率比较与分析
因为识别率主要受训练采样数与特征维数的影响。本研究分别使用1~9幅CASIA数据进行仿真训练,并搜索识别率最高时的特征维数。先将初始三维点云转换成人脸五官低维坐标,再将不同层次的特征进行组合,最后进行Matalab仿真,如图2所示为实验结果。实验证实二维主成分分析、Sin-K2DPCA识别率高于主成分分析,在每类9幅训练图像的情况下识别率分别达到91.9%和94.6%,而主成分分析在此条件下识别率仅为86%。训练图像越多识别率越高,尤其在小样本的情况下,Sin-K2DPCA的识别率达到71.2%的准确率,比之主成分分析的45%有显著的提高。
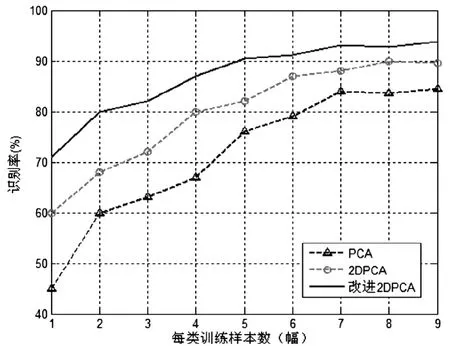
图2 不同训练样本数识别率比较Fig.2 Comparison of recognition rate of different training samples
3.2 算法实时性比较与分析
训练的计算复杂度也是衡量一个算法好快的关键因素,因此本研究对算法的识别时间进行分析。训练的计算复杂度主要集中在类特征生成和散度矩阵特征向量的生成,主成分分析法求特征值时使用SVD定理,将求解矩阵问题转化为空间问题。而Sin-K2DPCA直接对图像进行处理,把大空间分割成许多小空间,这样极大程度地提高了运算速度。此外主成分分析法特征生成耗时最长,所以在大样本的时候实时性较差。
识别时间由特征生成时间与特征比对时间组成。从表1里可以看出,Sin-K2DPCA结合了主成分分析和非线性的二维主成分分析的优点,其特征生成速度接近二维主成分分析,特征比对时间接近主成分分析,从而识别用时最少,实用性最好。Sin-2DPCA搜索时间仅需5.89秒,完全满足人脸识别的实时性需求。
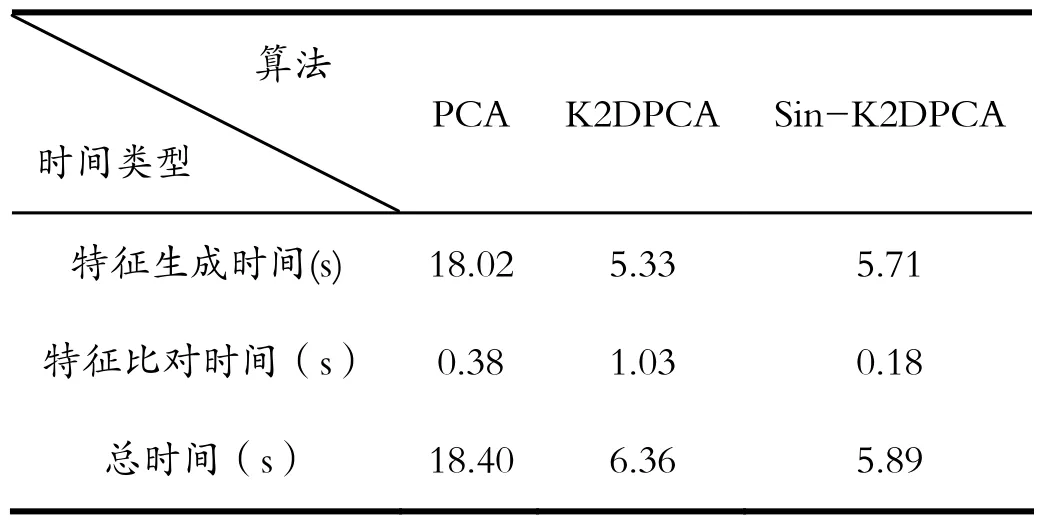
表1 三种算法识别时间比较Tab.1 Comparison of recognition time of three algorithms
4 结语
本文针对人脸表情、姿态同时存在时,人脸非刚性区域存在形变且三维点云数据缺失的问题,提出了一种基于Sin-K2DPCA的三维人脸识别,(1)通过点云模拟脸部的五官信息,捕捉脸部的复杂结构,将三维点云转换成脸部五官低维坐标;(2)通过改进的PointNet++网络将不同层次的特征进行多数据融合,提高特征的提取能力;(3)再应用Sin-K2DPCA进行Matalab仿真。通过仿真实验表明:本文提出的算法,降低了计算复杂度,对二维训练集孤立点的鲁棒性优于K2DPCA,对于三维数据集Sin-K2DPCA克服了由于计算量大K2DPCA不能实现的问题。不仅提高了三维人脸识别的准确率,同时识别时间也明显缩短。
