大问题厘清知识逻辑 大环节推进数学思考

胡佳丹 莫延安

【摘 要】以往人教版数学三年级下册第六单元《年、月、日》的教学，无论是教材的设计，还是名师的课堂展示，都只注重教师的主导作用，学生作为学习主人这一地位没有得到更好的体显。因此本文采用“课前学生提出问题——课中梳理问题、解决问题——再次提出问题，巩固知识”这样大问题、大板块、大环节设计的教学实践尝试，有效地提高了学生提出问题、解决问题的能力，帮助学生厘清了知识点之间的逻辑关系，促进了学生的数学思维发展。

【关键词】问题提出 大问题解决 数学思考

《年、月、日》是人教版数学三年级下册第六单元的教学内容，知识点碎而多，传统的教学往往是让学生通过观察和梳理年历表，得出大、小月及二月的规律，再引导学生计算一年有几天。这样的教学非常零散，学生每一步都要按教师的指令操作，不能激发学生的学习兴趣，更不能帮助学生积累学习活动的经验、激发他们的潜能。我们设想用大环节、大问题、大板块的理念设计本节课的教学，任务一根据年历表提出数学问题，任务二以“一年有几天”这个大问题的解决来梳理知识点，任务三根据信息再次提出问题，在解决问题的过程中巩固有关年、月、日的知识。

教学任务一：观察年历，提出数学问题

（出示2014—2021年的年历表）

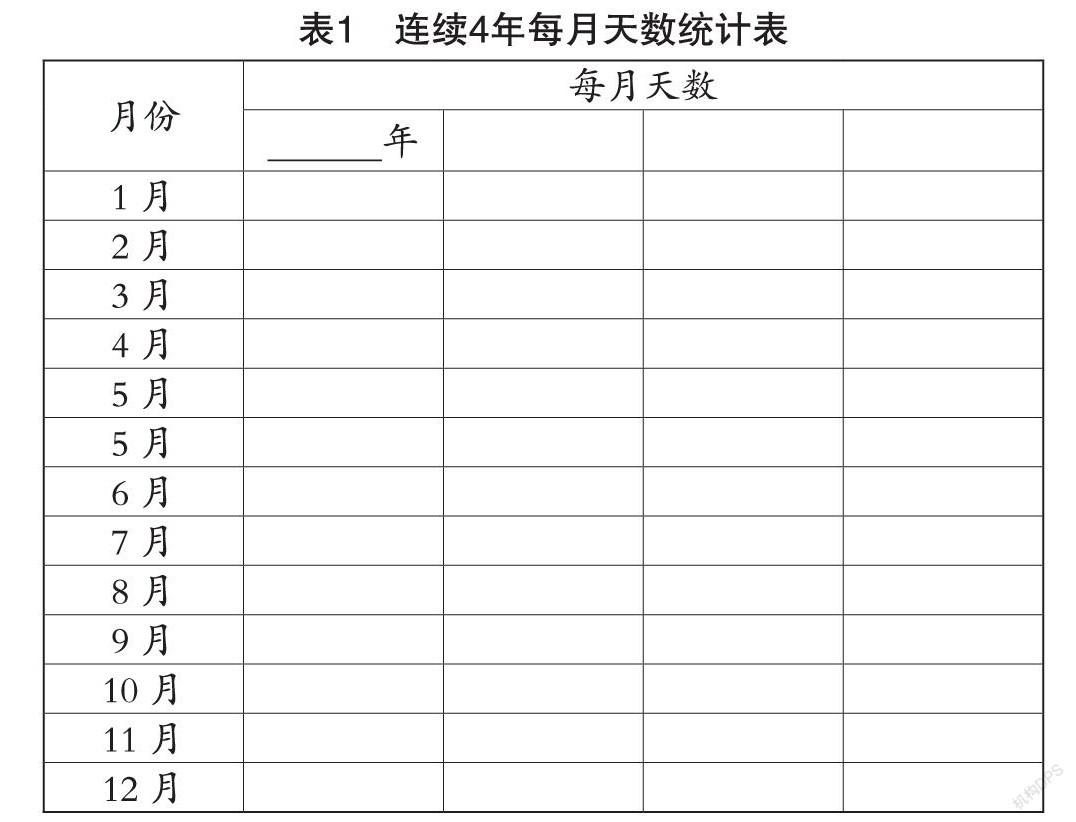
1.观察年历表，选择连续的4个年份，完成下面的统计表。（见表1）

2.根据年历表和统计表，你能提出哪些数学问

题：

3. 梳理问题，分类整理。

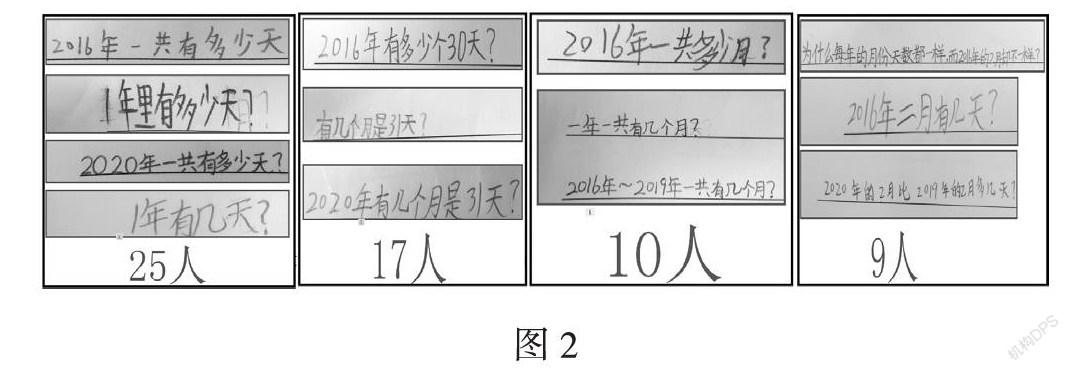
本次课前下发提问表35份，经统计和整理，发现学生提的有效问题主要分为三类。

第一类：跟年、月、日基础知识有关的，是本节课要解决的主要问题，也是问题提出人数较多的。

问题1：关于一年有多少天？（25人）

问题2：关于一年有几个月是31天的？有几个月是30天的？（17人）

问题3：关于一年有几个月？（10人）

问题4：与2月相关的问题，如2016年的2月有几天？为什么每年的其他月份天数都一样，但是2月不一样？（9人）

第二类：多以为什么的形式出现的问题，是学生的疑问，且难以解答。例如：为什么每个月的天数不一样？为什么要发明“年”？为什么一年有12个月？这些问题，是知识背后的原因，涉及天文学以及历史传说，可在课中以视频播放、呈现学习资料的形式进行拓展学习。

第三类：主要是涉及计算经过的天数问题，如图1。

因为这些问题是例3的内容，所以本节课不呈现。

【设计意图】三年級学生已经学过的时间单位有时、分、秒，同时年与日的知识在生活中也有所接触，但是他们对年、月、日的具体知识的了解是比较粗浅的。所以，本课以问题提出的形式展开教学，以期将学生头脑中模棱两可的知识和概念转化为清晰的知识体系。

教学任务二：解决数学问题

（一） 复习旧知，导入新课

今天这节课，我们就来学习年、月、日有关的知识。（出示课题：年、月、日）

（二）自主探究，解决问题

1.以“一年有几天”为核心问题，引领梳理年、月、日的知识点。

（1）下面，我们一起来解决同学们刚才提出的几个问题（PPT展示学生的问题，如图2），从提问人数最多的这个问题开始—— 一年有多少天？

生1：2020年的天数=31+29+31+30+31+30+31+31+30+31+30+31=366（天）。

师：从上面的算式中你还发现了什么？

生2：一年有12个月。

师：是的，这种方法还解决了我们提出的第三个问题，也就是一年有12个月。

生3：31×7+30×4+29=366（天）。

引发学生思考：31×7表示什么意思？这7个月分别是哪几个？30×4表示什么意思？这4个月分别是哪几个？

根据学生的反馈，板书：

①有31天的月份是：1、3、5、7、8、10、12，共7个月。

②有30天的月份是：4、6、9、11，共4个月。

师追问：除了2020年，其他年份也是如此吗？学生结合课前统计表，观察年历表。

观察发现：每年都是有7个月31天，分别是1、3、5、7、8、10、12月;有4个月是30天，分别是4、6、9、11月。每个月31天的叫大月，每个月30天的叫小月。

【设计意图】数学知识是严密的，所以不能仅以2020年为例，就推断出大小月，必须建立在多年份的年历观察的基础上，这样学生才会从实际的观察中主动地发现这些共同的特征并主动地认可大小月的知识。

师：你有什么好方法来记住哪几个月是大月，哪几个月是小月吗？（拳头记忆法，歌诀记忆法）

（2）继续提问：29是几月的天数？（2月）

追问：为什么可以用“31×7+30×4+29”来计算？其他年份也可以这样来计算吗？

学生利用年历表，观察历年2月份的天数，共同完成2月份天数统计表，发现每4年中有一个2月是29天，其他三年的2月是28天。

师：看来2月确实很特殊，所以我们把它叫做特殊月。2月是28天的年份，一年有365天;2月是29天的年份，一年有366天。我们把一年是365天的年份叫平年，一年是366天的年份叫闰年。

（3）引导学生提问：学到这里，你有什么问题？（平年和闰年是怎么来的？）

视频介绍平闰年的由来，简述四年一闰，百年不闰，四百年又闰的规律。

（4）同学们，我们在解决这个问题的过程中，用到了哪些知识？再回过头来看看问题，你有什么发现？

引导学生发现：解决了一年有几天这个问题，其实也就是把刚才提出的这些问题都解决了。所以，数学知识是互相联系的整体，数学问题也是环环相扣的，这就是数学的魅力。

【设计意图】年、月、日的知识如果是按常规的逻辑：从一年有12个月，7个大月，4个小月，2月有28天或29天一步一步开展教学，并最终计算一年有几天来进行大小月的巩固，其实学生是被动地在接受知识并运用知识进行计算。本课反其道而行之，目的在于用一个问题引发学生思考，引领学生完成年、月、日知识体系的构建，在解决一年有几天的问题的过程中，学生通过观察、归纳、对比，寻找所需解决问题的条件，从而解决其他小问题的过程，并在这个过程中，发现数学知识的联系性。

2.以“为什么”为拓展问题，激发学生探究知识成因的兴趣。

（1）自主阅读小资料，解决：

（2）观看视频，了解：

【设计意图】年、月、日知识背后的原因，是学生感兴趣的点，通过课外知识的补充，能激发学生的探索兴趣，扩大学生的知识面，也能让学生在学习知识的过程中，知其然并知其所以然。

教学任务三：知识巩固，在练习中再一次提出问题并解决问题

1.根据情境，提出年、月、日有关的数学问题。

某班组织同学们连续跳绳打卡，为期两个月。小洪同学的妈妈为他准备了60页的打卡记录本，每天一页进行记录。

经过一段时间坚持小洪同学看着日历本说，“太好了今天是26日了，到月底就完成咯！

生1：小洪还有几天就能完成任务？

生2：小洪一共要跳几天绳？

生3：打卡记录本一共要几页？

生4：60页的打卡记录本够用吗？

经过师生讨论，生2和生3是同一个问题，可以合并成一个。而要解决“小洪还有几天就能完成任务”必须先解决“小洪一共要跳几天绳”，因此，确定解决问题的顺序为：①一共要跳几天绳？②60页的打卡记录本够用吗？③还有几天就能完成任务？

2.自主思考，解决问题一：一共要跳几天绳？

（1）学生自主探究。

（2）交流汇报，分析讨论。

在分析讨论中进一步归纳发现：连续2个月可能是2个大月、1个大月和1个小月、闰年2月和大月、平年2月和大月这四种情况，不可能出现连续2个小月的情况。完善结果为：

情况一：（大）月和（大）月，算式： 31+31=62（天） 。

情况二：（大）月和（小）月，算式： 31+30=61（天）。

情况三：（大）月和（闰年2）月，算式： 31+29=60（天）。

情况四：（大）月和（平年2）月，算式： 31+28=59（天）。

3.根据问题一的情况，口答问题二：60页的打卡记录本不一定够。

4.小组合作解决问题三：还有几天就能完成任务？

生1：大月：26、（27）、（28）、（29）、（30）、（31），還要5天。

生2：小月：26、（27）、（28）、（29）、（30），还要4天。

生3：闰年2月：26、（27）、（28）、（29），还要3天。

生4：平年2月：26、（27）、（28），还要2天。

【设计意图】设计这一任务的目的在于让学生能将所学的年、月、日知识运用到实际生活情境中，培养学生根据情境提出问题、解决问题的能力。另一方面，打开学生思路，让学生感受到，因为大小月的不同，所产生的答案也会不同。最后，在这些问题的解决中，回顾年、月、日的知识，并发现一些特点。

教学反思

（一）大板块、大问题、大环节的设计

本节课的设计以两次问题提出展开教学，只设计了三个环节、三个教学任务。考虑到本节课知识点多、碎，把问题提出环节放在课前作为预习作业，以“一年有几天”这个学生提出人数最多的问题展开教学，这个大问题演绎出一系列的小问题，从加法算式“31+29+31+30+

31+30+31+31+30+31+30+31”中可以得到一年有12个月，从“31×7+30×4+29”中得到大月、小月、2月的概念与规律。这一反向设计，不仅因为这个核心问题涵盖了全课所有知识点，学生提出的其他三个关于年、月、日知识的问题都在解决这个问题的过程中得到解决，而且利于学生从更高的维度构建年、月、日知识体系，也让学生体会到复杂问题是由简单问题组成的，逐个解决简单问题就有可能最终解决复杂问题。

（二）统计表起到“脚手架”的作用

课前先观察年历表，完成连续4年的月份天数统计表，然后提出问题。这里连续4年的月份天数统计表起到了“脚手架”的作用，在其他班级试教时，直接让学生观察年历表后提出问题，由于学生观察不深入、体验不具体，很多学生提出的问题没有涉及数学本质，提出了很多非数学问题，如：“为什么每个月里都有一个数被横线划出来？”“2020年10月14日为什么被圈起来？”有了统计表，学生在填写的过程中会进行简单的观察、分析、思考，提出的问题更有针对性。

（三）以再次提出问题的形式设计练习，富有挑战

本节课的练习设计，没有使用常规练习那种出示具体月份判断大、小月的形式，而是只设计了一道题目，请学生根据信息提出问题，以问题为任务驱动，激发学生学习兴趣。把年、月、日所涉及的知识点有机整合在学生熟悉的跳绳、打卡等场景里，既符合学生的生活实际与心智发展水平，又具有逻辑结构性，使学生在解决具体的生活问题的过程中，学会应用、消化、内化知识。从教学效果来看也相当好，学生提出了三个问题，在解决问题的过程中发现，答案是开放的，涵盖了本节课所有的知识点，要解决问题需要综合本节课所有的知识点来考量，富有挑战性。学生在提出问题、解决问题过程中经历各种峰回路转，发现了一年里有可能有2个连续的大月，但不可能有2个连续的小月，更发现了跨年的12月和1月是连续的大月，进一步完善了年、月、日的知识结构。

（四）课外资料的多维补充

“心中有数学，更要心中有学生。”在学生提出的问题中有很多“为什么每个月的天数不一样”“为什么2月份的天数特别少”“一年为什么有12个月？不是10个月”等学生感兴趣的问题，我们以“阅读资料、视频”等形式呈现，有助于将《年、月、日》单元的内容呈现得更为饱满，教学做到知识与趣味相结合，基础与拓展相连接。