基于气候突变年的太阳辐射模型统计时长选取方法
2021-12-21贾晓宇
于 瑛,贾晓宇,陈 笑
(西安建筑科技大学 机电工程学院,西安 710055)
在全球变暖和环境污染的背景下,太阳能作为清洁可再生能源中的重要组成部分,越来越受到人们广泛关注[1]. 太阳辐射数据在建筑、工业、农业等领域的研究中有着深远的意义,但由于经费、设备维护困难等方面的原因,只有少量台站能够测量太阳辐射. 在我国有气象台站2500多个,辐射台站仅有98个,其中记录散射辐射数据的台站17个,数量远少于气象台站. 太阳辐射观测数据远远不能满足需求,辐射数据的缺乏成为制约太阳能应用的主要因素之一[2]. 因此,利用易于测量的气象参数估算太阳辐射,成为补充太阳辐射数据的重要方法之一.
国内外学者提出了许多利用气象参数来估算太阳辐射的方法,主要包括:基于太阳辐射与气象参数之间的关系开发出的不同类型的经验模型[3],人工智能模型[2,4],自适应神经模糊推理系统(ANFIS)[5]以及基于卫星的衍生模型[6]. 文献调研发现,不论使用哪种模型,国内外学者在建立太阳辐射模型时都采用了不同的建模时长. 例如Li等[7]用1994年-2004年的数据,分析了8种模型的误差,Wu等[8]用1994年-2005年的数据,对多种模型进行了比较,Janjai等[9]用柬埔寨三颗卫星1995-2008年的数据,估算了柬埔寨地区的太阳辐射,Chen等[10]用1976年-2000年数据建立了支持向量机(SVM)的模型,估算东北地区的太阳辐射量. 建模时长从小于5年[11]、5年到10年[7,12]、10年到20年[8-9,13],大于20年[10,14]不等,但选择建模时长的原因及建模时长对于模型估算误差的影响在前期的文献中并没有明确讨论.
从统计学角度,在气象要素与太阳辐射关系相对稳定的情况下,往往较长的统计时长意味着可以得到可靠的模型参数. 然而研究表明,全球近50年来日照时数、降水、温度等气候要素发生了变化,且不同地区的变化时间以及程度各不相同,地面太阳总辐射也出现了从减少到增加的变化过程[15]. 如果建模统计时段使用了过多的历史数据则会削弱这种变化的影响,使模型不能很好地表征当前气象参数与太阳辐射之间的关系,所以选取统计时长时有必要考虑气候变化带来的影响.
鉴于此,本文提出一种借助气候突变年选取太阳辐射模型统计时长的方法. 将气候突变年作为选取太阳辐射模型建模时长的时间节点,选取不同建模时长来建立太阳辐射估算模型,通过比较模型误差判断该方法的可行性. 本文主要完成如下工作:1)选择与太阳辐射相关性较强的日照时数、温度、相对湿度表征气候变化,采用Mann-Kendal突变检验法对90个台站温度和相对湿度进行突变检验,采用累积距平法对日照时数进行突变检验;2)利用变差系数法分别计算3个气象要素的权重,进而确定各台站气候突变年;3)以气候突变年作为选取建模统计时长的时间节点,分别建立日总辐射模型和散射辐射模型,比较选取不同统计时长时模型误差,证明借助气候突变年选取太阳辐射模型统计时长方法的可行性.
1 数据获取及质量控制
本文选取日总辐射数据记录超过25年的90个台站和日散射辐射数据记录超过25年的12个台站作为研究对象. 本文所用数据来自“中国地面气候资料日值数据集”和“中国辐射日值数据集”,上述数据集获取时间截止2017年12月31日.
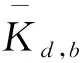
2 气候突变年的确定
气候突变是指气候从一种稳定状态跳跃式地转变到另一稳定状态的现象[17]. 温度、湿度、降水、大气压等气象要素常被用来表征气候突变. 白晶等[18]对年平均气温和降水进行突变检验来表征气候变化,洛桑卓玛等[19]对西藏地区降水量进行突变检验来表征气候变化,赵芳芳[20]对气温、降水量和日照时数进行突变检验来表征气候变化. 太阳辐射与气象要素之间有着密切联系,在众多气象要素中,日照时数、温度、相对湿度与太阳辐射相关性较强[21],所以本文选择这3个气象要素进行突变检验来表征气候变化,进而判断气候突变年.
气象要素突变检验的方法有很多,常用的有Mann-Kendall(M-K)法,滑动t检验法[17],Yamamoto法,累积距平法[22]等. 由于气象要素变化特征不同,所以不同气象要素采用的突变检验方法也不相同. M-K检验法作为一种非参数检验方法,假定了随机变量的分布,不需要样本遵从一定分布,不受少数异常值干扰[17],在温度与湿度的突变检验中有很强的适用性,所以本文采用M-K法对温度、相对湿度进行突变检验. 累积距平法在日照时数突变检测中广泛应用且结果较好,故本文采用该方法对日照时数进行突变检验. 考虑到3个气象要素突变检验结果年份会出现不一致,所以采用变差系数法[22]进一步计算各个气象要素对气候突变的影响权重,将权重最大的气象要素所对应的突变年确定为气候突变年.
我国地域辽阔,各区域气候环境各不相同,本文选取分布在我国东北部、西部、北部、南部的4个代表台站为例说明气候突变年的确定方法. 台站具体信息见表1.
2.1 气象要素突变检验
2.1.1 温度
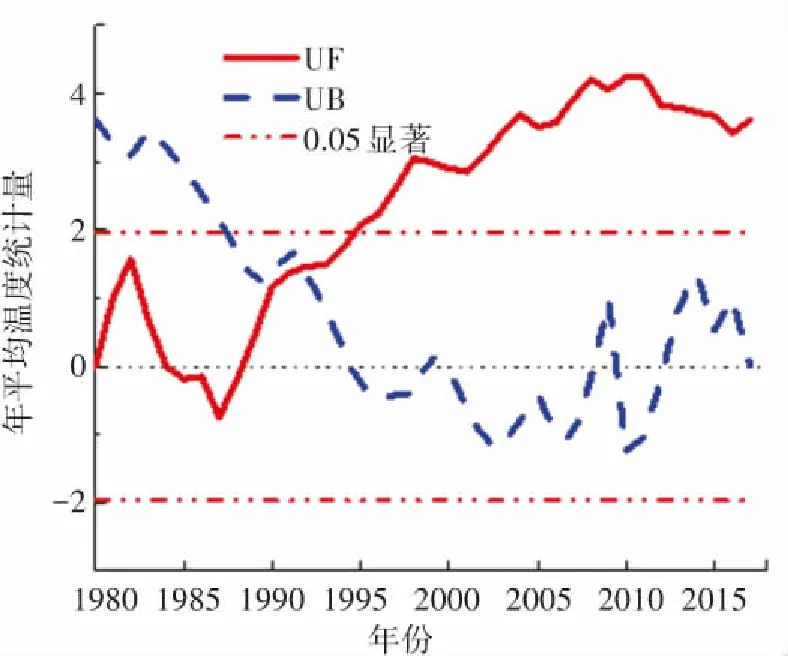
温度是一种表示空气冷热程度的物理量, 它是气候变化的重要指标. 本文对4个代表台站年平均温度进行M-K突变检验. 图1为4个台站年平均温度M-K突变检验图(其中UF代表正向时间序列统计值,UB代表逆向时间序列统计值),由图1(a)中可知UF曲线在1987年出现一个波谷后持续上升,可见在此期间哈尔滨年平均温度总体呈上升趋势. UF曲线在1980年~1993年并未超过+1.96信度线,说明平均温度缓慢上升,1993年后UF超过+1.96信度线,表明1993年后年平均温度明显升高. 图1(a)中UB曲线和UF曲线在0.05置信区间中只有一个交点,该交点对应的横坐标为1992年,该年即为哈尔滨的温度突变年. 按照相同的方法可得喀什、锡林浩特、福州温度突变年分别为1999年、1993年、1989年,如图1(b)、(c)、(d)所示.
(a)哈尔滨
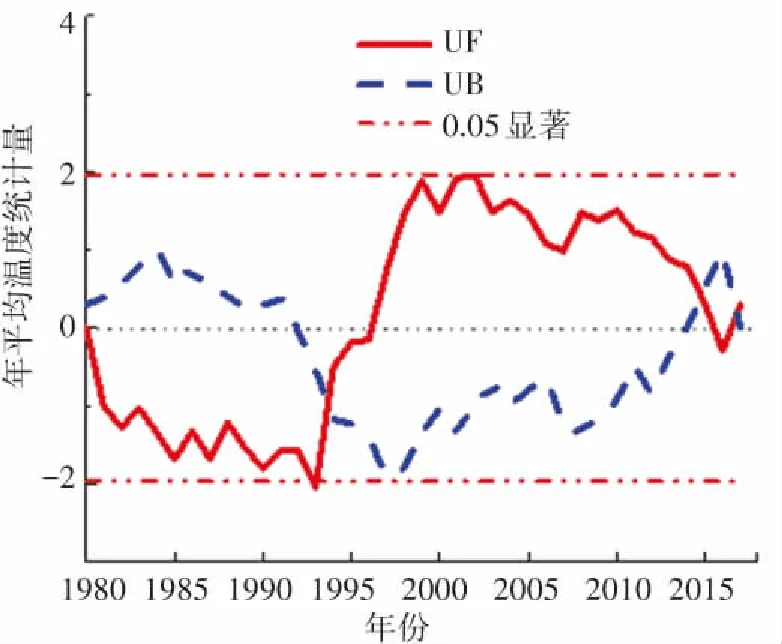
(c)锡林浩特
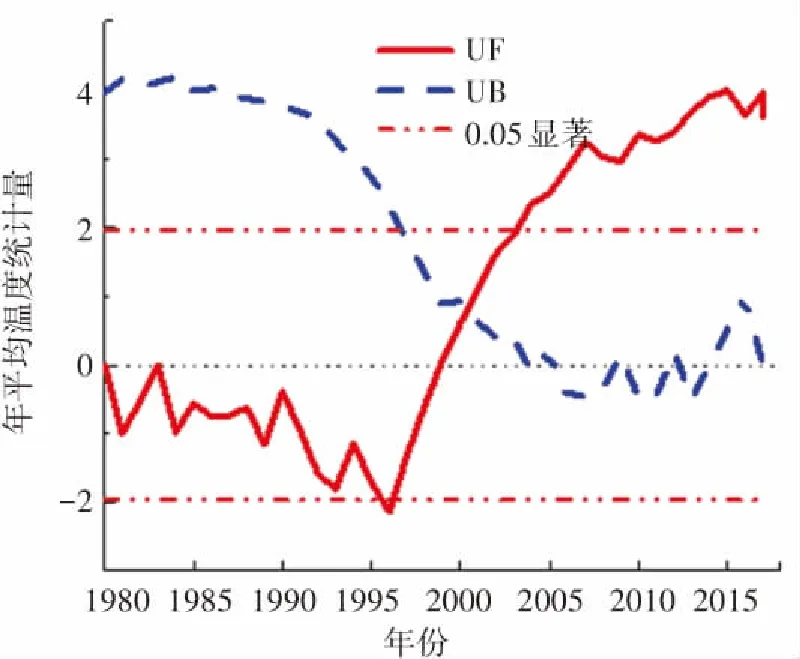
(b)喀什
2.1.2 相对湿度
相对湿度表示在一定温度条件下,空气中的水蒸气含量距离该温度条件下饱和水蒸气量的程度. 4个代表台站年平均相对湿度M-K突变检验如图2所示,由图2(a)可以看出哈尔滨年平均相对湿度UF曲线1980年到1985年之间在0刻度线上下波动,说明该时段平均相对湿度基本稳定,从1985年到2006年曲线缓慢下降,2006年后UF小于-1.96信度线,此后年平均相对湿度出现明显下降,2013年到2017年之间年平均相对湿度又出现小幅上升. 相对湿度的波动使得UB曲线和UF曲线的在0.05置信区间中有3个交点,对应的横坐标分别为1982年、1984年和1986年. 当M-K法检验出多个突变年时要采用滑动t检验法进一步检验,最终确定1个突变年. 滑动t检验是通过比较不同时间序列内数据平均值的差异是否显著,进而检验突变的一种方法. 通过滑动t检验法对3个突变点进行检验, 最终确定气候突变年为1986年. 使用同样的方法检验喀什、锡林浩特、福州的相对湿度突变年,结果分别为2004年、1996年、1996年,如图2(b)、(c)、(d)所示.
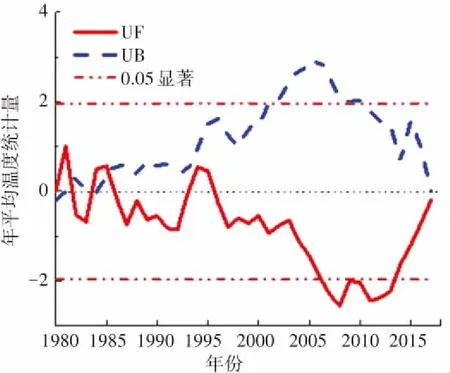
(a)哈尔滨
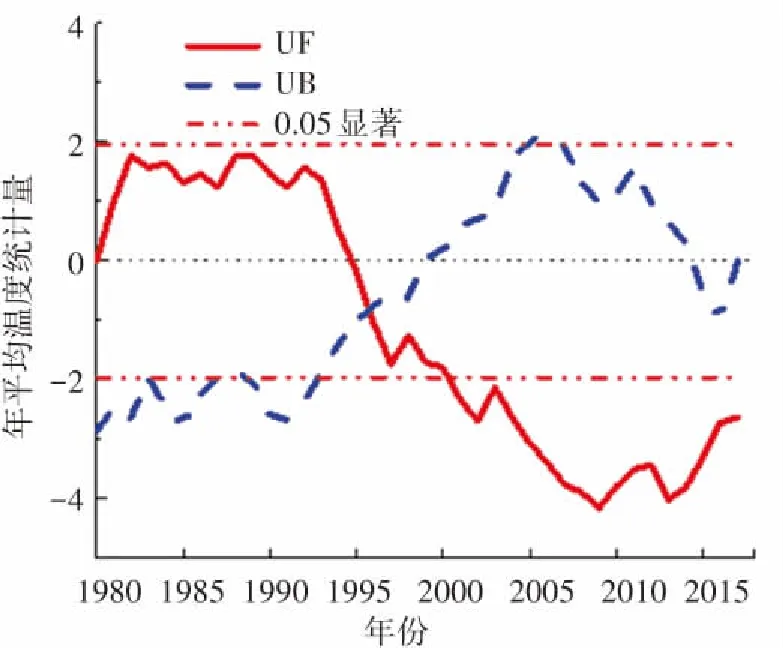
(c)锡林浩特
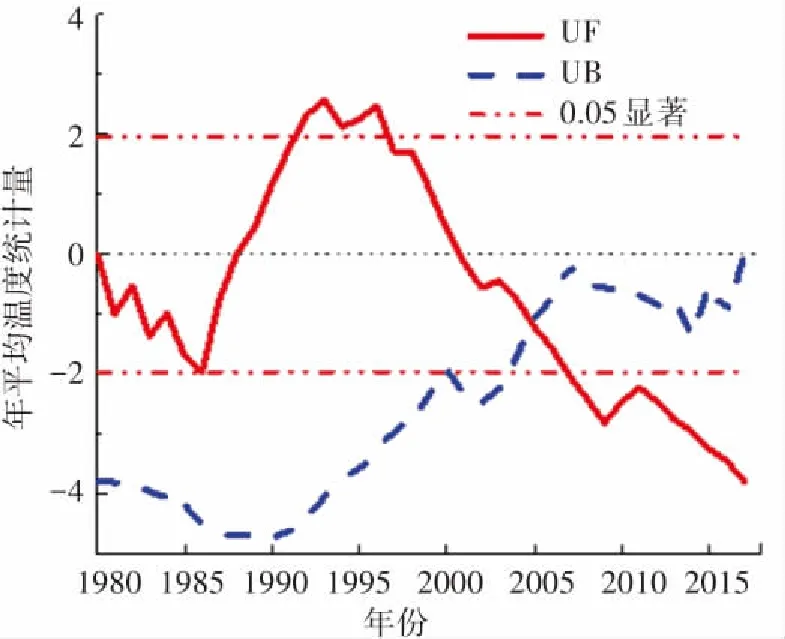
(b)喀什
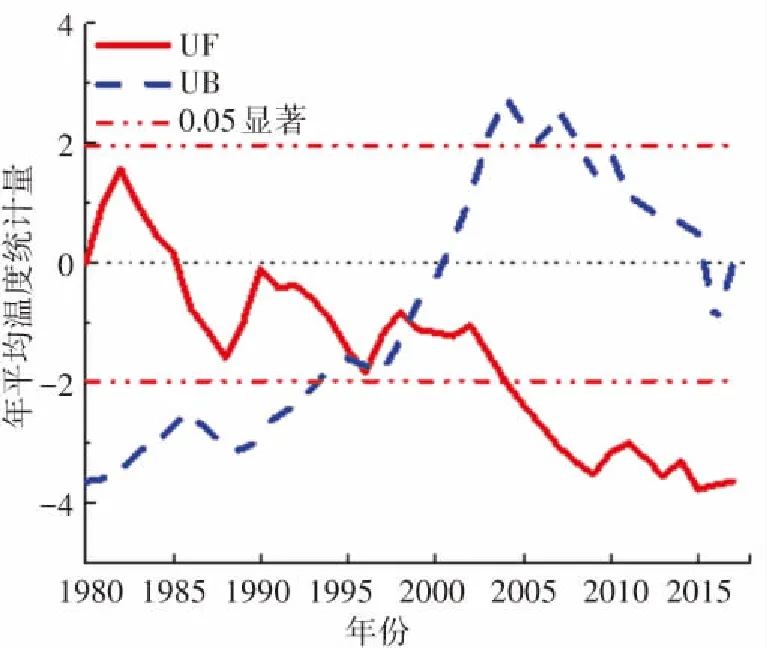
(d)福州
2.1.3 日照时数
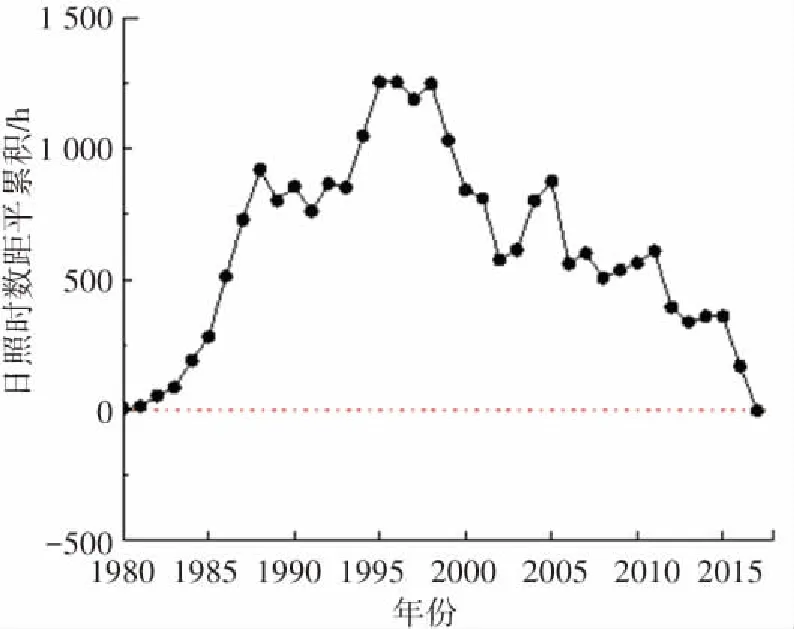
日照时数指一天内太阳直射光线照射地面的时间,从一定程度上反映了该地区接受太阳辐射的情况. 本文采用累积距平法对年总日照时数突变年进行检验. 图3为4个代表台站的日照时数累积距平图,以图3(a)哈尔滨为例,年总日照时数累积距平值在1991年与0刻度线最远,根据累积距平算法原理可确定该年为日照时数突变年. 使用同样的方法计算喀什、锡林浩特、福州日照时数突变年分别为1993年、2003年、1994年,如图3(b)、(c)、(d)所示.
2.2 气候突变年确定
上文通过M-K法和累积距平法得到各气象要素的突变年,如表2所示,显然相同台站不同气象要素突变年检验结果并不相同,因此气候突变年的确定要考虑不同气象要素对气候突变的影响权重. 变差系数法是一种基于熵原理的权重确定方法,即熵越大,则权重越大[22]. 变差系数计算公式如(1)所示:
(1)
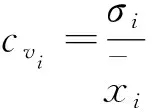
按照上述方法计算90个台站气候突变年,如图4所示,可见由于台站所处的气象条件、地理位置、人口、经济发展水平等因素各不相同,气候突变年有较大差异. 但仍能发现大多数站点气象突变年集中在1996年、2002年和2006年附近,该结果与一些研究地域突变年的文献结果基本一致[18-20]. 从图4中可以看出一些地理距离较近、气候条件相似且经济发展水平、人口数量等因素相当的台站突变年相近,例如:广州和汕头;喀什、和田和哈密;固原和银川,丽江、腾冲和昆明等. 但也出现地理位置接近,但地区经济发展水平、人口数量等因素相差较大的台站,比如峨眉山和绵阳;杭州和洪家等. 可见,气候突变年不但与气象要素有关,也与当地经济发展状况、产业结构、人口密度等其他因素有关.
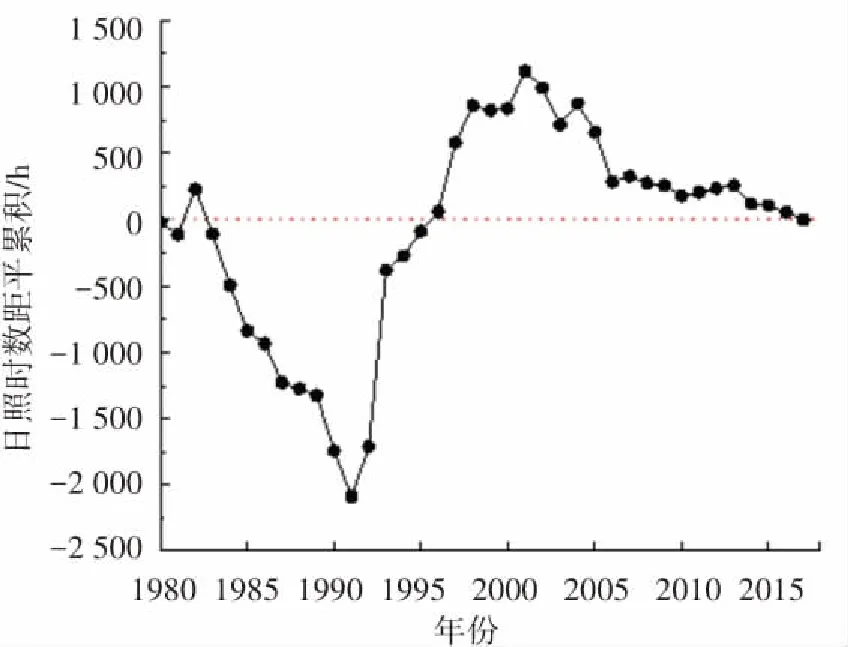
(a)哈尔滨
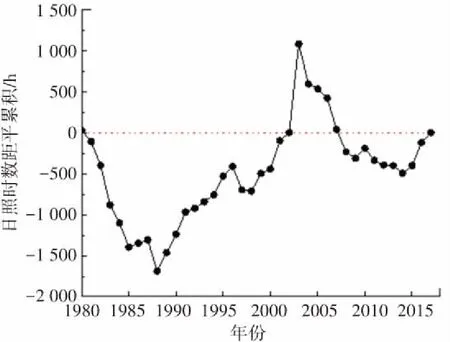
(c)锡林浩特
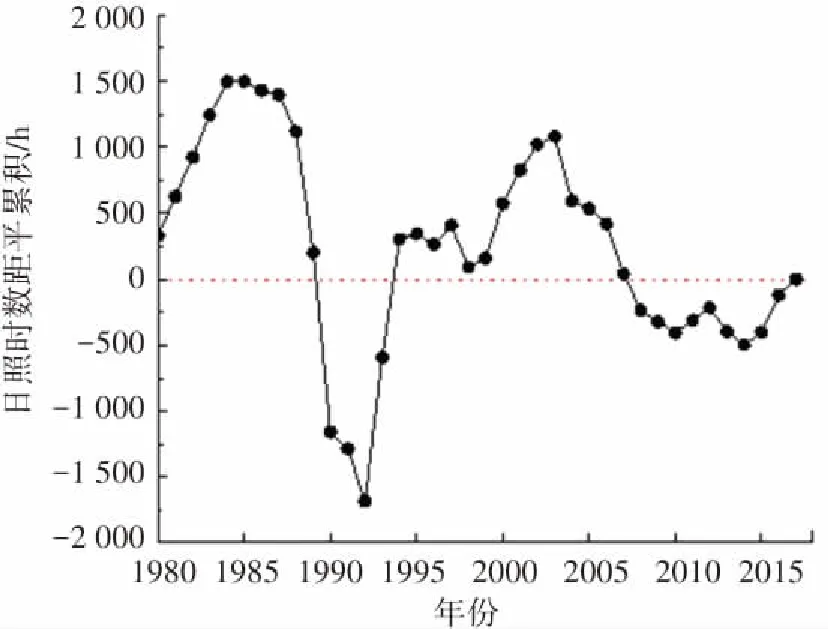
(b)喀什
(b)福州
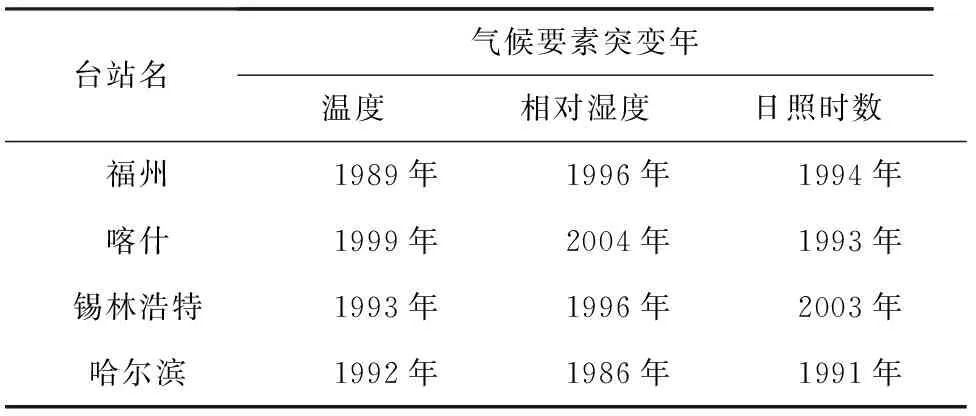
表2 代表台站气象要素突变年
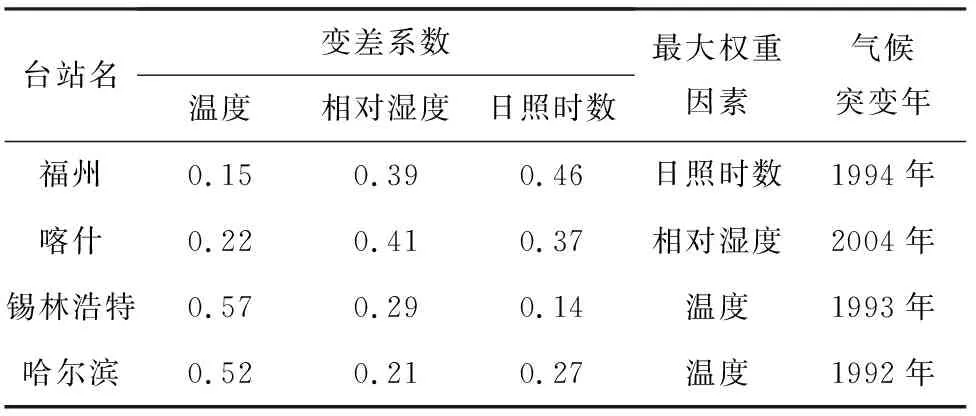
表3 代表台站气候突变年

图4 90个台站气候突变年
3 统计时长对模型估算误差的影响
3.1 模型选择和建立
本文以日总辐射模型和日散射辐射模型为例,以气候突变年作为选取模型统计时长的分界点,选取不同的统计时长建立模型,分析统计时长对模型估算误差的影响.
基于日照时数比的日总辐射估算模型最早是由Angstrom在1940年提出,1942年Prescott对此模型做了修正,因此习惯称之为Angstrom-Prescott模型(AP模型),见公式(2),该模型结构简单易于计算且在大多数气候环境下都适用,是目前应用最为广泛的日总辐射估算模型[21,23]. 散射模型采用基于晴空指数与日照时数比的模型,该类模型是晴空指数和日照时数与散射比Kd(水平面散射辐射量与水平面日总辐射量之比)产生一次、二次及三次多项式函数关系,其中三次多项式模型(公式(3))在我国适应性较好[24]. 针对以上2个模型,分别选择2个不同统计时长建模,从统计学角度来看,统计时长越长模型参数越准确,因此模型GⅠ和DⅠ选择的建模时长为记录数据起始年至2013年;模型GⅡ和DⅡ借助气候突变年选取建模时长,建模时长为气候突变年至2013年. 模型验证时段统一选择2014年至2017年,模型信息如表4所示.
(2)
Kd=a+bKt+cKt2+dKt3+
(3)
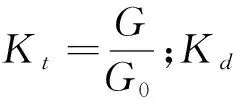
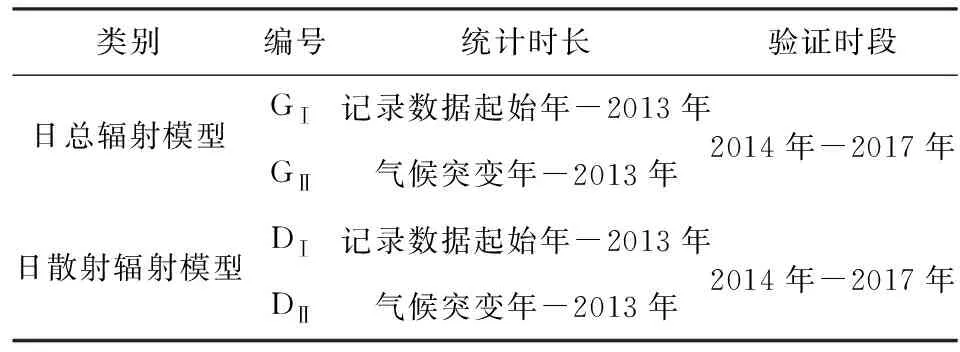
表4 模型信息
3.2 模型评价指标
由于台站所处地理位置不同和气候条件各异,造成台站之间观测数据量值本身存在较大的差异,为了消除其对估算误差的影响,更加客观地评价模型的精度,引入均方根误差百分率RMSE%(Percentage Root Mean Square Error),数学表达式如公式(4)所示,为了评价模型的拟合程度引入决定系数R2,见公式(5). RMSE%越小表示模型误差越小,R2的取值范围为0~1,R2越接近1则模型与实际值的拟合程度越高.
(4)
(5)
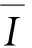
为了评价不同建模时长对模型估算误差的影响,引入ERMSE%(Errorof Percentage Root Mean Square Error),见公式(6). 当ERMSE%为负值时说明模型GⅡ和模型DⅡ优于模型GⅠ和模型DⅠ.
ERMSE%=ⅡRMSE%-ⅠRMSE%,
(6)
式中ⅠRMSE%为模型GⅠ和DⅠ的RMSE%,ⅡRMSE%为模型GⅡ和DⅡ的RMSE%.
3.3 估算误差分析
分别计算2个统计时长模型估算误差,并进一步求出ERMSE%. 90个台站的日总辐射模型R2及估算误差如图5所示. 图5(a)中可见采用模型GⅡ可以提高与观测数据的拟合度,最多可提高0.2,平均提高0.05. 图5(b)中77个台站的ERMSE%为负值,约占总数的85%,ERMSE%最小可达-5%,平均值约为-2%. 说明以气候突变年为时间节点,选取其后的数据建模,可以提高模型拟合度,有效降低模型估算误差. 误差降低越显著从另一个侧面也说明该台站气候变化越明显.
如前文所述,我国地面辐射观测站中仅有17个台站记录散射辐射数据,从中选择数据记录超过25年的12个台站建立散射辐射模型,模型R2和估算误差如图6所示. 图6(a)中显示,由于散射辐射模型采用多参数输入的3次模型, 2个模型的拟合程度均超过0.8,在采用该方法后模型决定系数R2整体有所提升,平均提升0.02,最多可提高0.06. 图6(b)中9个台站ERMSE%为负值,占站点总数的75%,ERMSE%平均值约为-2%,最小可达-5%.
通过以上分析发现,虽然模型类型不同,但采用气候突变年后数据建模均可以有效降低模型估算误差,提高模型拟合程度,且ERMSE%与R2分布相似,说明了借助气候突变年确定建模统计时长的方法是有效的,且结果具有稳定性.
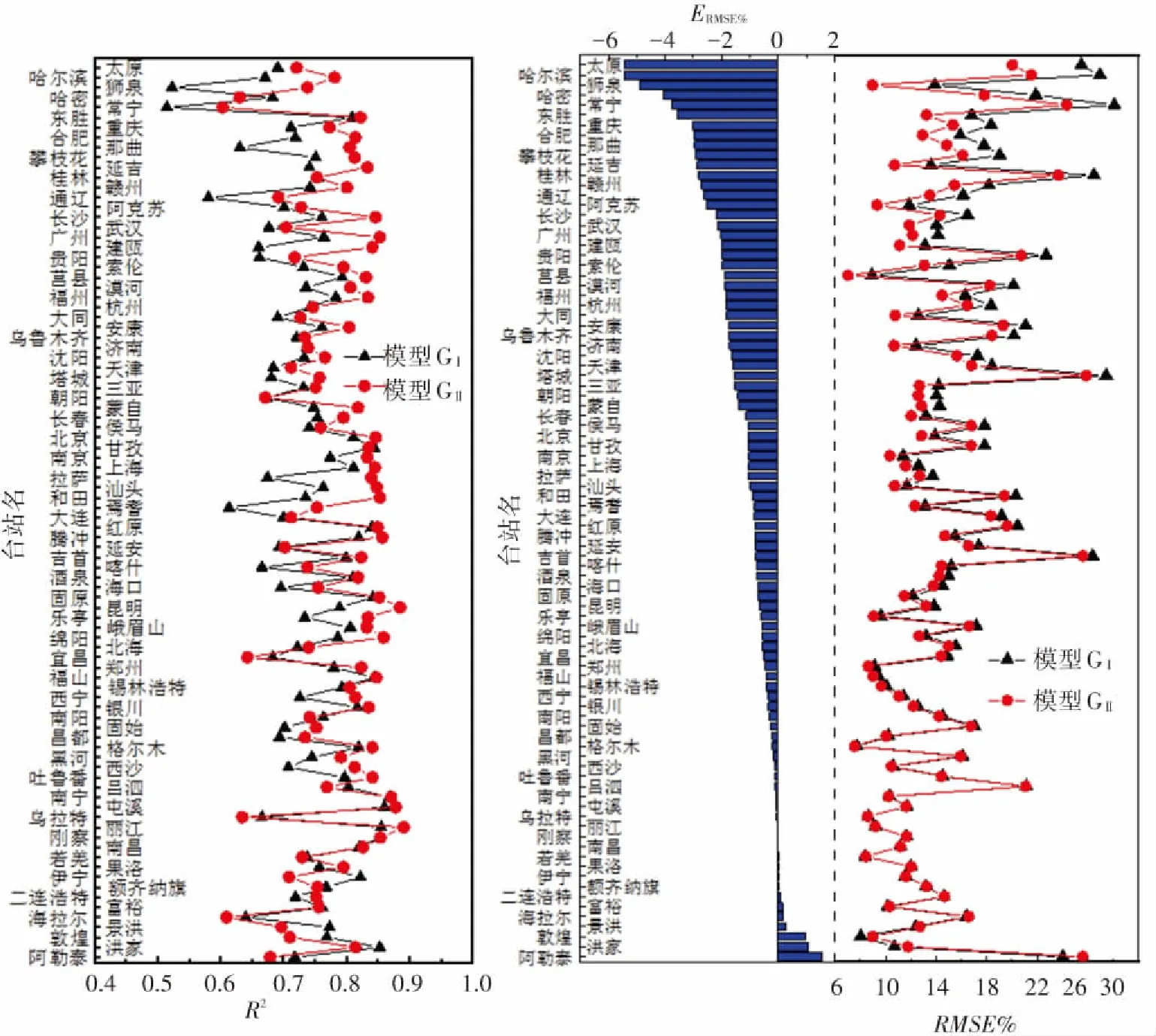
(a)R2分布 (b)误差分布
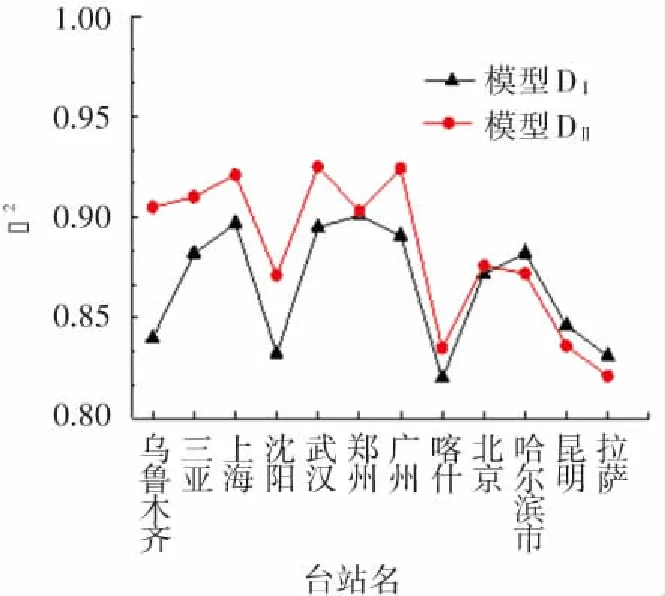
(a)R2分布
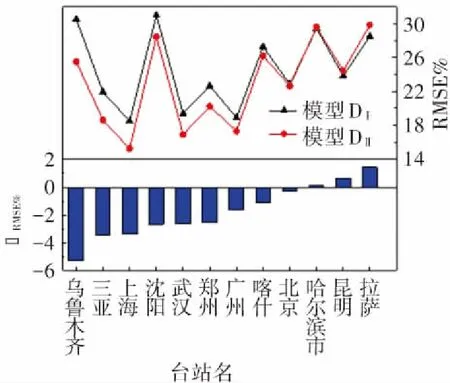
(b)误差分布
4 结 论
针对辐射模型建模统计时长的选取问题,本文提出一种借助气候突变年选取建模统计时长的方法,利用该方法建立了太阳辐射模型并对模型误差进行分析,得到以下结论:
1) 借助气候突变年的判别方法,对我国90个台站进行气候突变年检验,发现75%的台站气候突变年均集中在1990年~2005年之间,说明近30年间我国大多数地区气候都发生了变化. 当台站之间地理距离相近,且经济发展水平、人口等因素相差不大时,气候突变年也相近.
2) 以突变年为时间节点,选取突变年后数据时段作为统计时长分别建立日总辐射模型和散射辐射模型,将模型估算误差与观测数据超过25年统计时长的模型估算误差比较,结果显示借助气候突变年选取建模统计时长的方法可以有效减少估算误差,提高模型拟合程度. 该方法可为太阳辐射模型统计时长的选取提供依据.
