人工智能在复合材料研究中的应用
2021-12-21张峻铭杨伟东
张峻铭 杨伟东 李 岩
同济大学航空航天与力学学院, 上海 200092
1 引 言
先进复合材料作为结构轻量化的重要原材料, 已在航空航天、轨道交通、土木建筑等重要工程领域中得到广泛应用, 而复合材料的用量占比如今已成为衡量飞机先进性的重要指标. 以民用航空领域为例, 国外的先进民航客机, 如波音公司的B787和空客公司的A350, 复合材料用量已达结构重量的50%以上, 而国产大飞机C919仅为12%, 复合材料应用技术落后国外20年(杜善义和关志东 2008, 宁莉等2020). 但是, 中俄正在联合研制的国产CR929远程宽体客机中, 复合材料用量计划达到50%以上. 在当前新形势下, 这一跨越式发展的目标对高性能复合材料的设计制造提出了新要求. 另一方面, 复合材料及其结构的性能预测、结构设计、工艺制造等全链条因素都会对其力学性能产生重要影响, 决定了复合材料的应用水平. 因此, 如何通过多尺度多维度的复合材料设计进一步减轻结构重量并实现卓越的力学性能? 如何优化创新成型工艺方法, 制造复杂复合材料结构并降低制造成本? 如何实现对复合材料服役状态的有效监测、提升复合材料使用寿命? 这些问题是信息化时代背景下, 力学研究者所面临的新机遇与新挑战.
传统的复合材料研究方法, 主要以实验和理论建模为主, 逐渐形成了实验观测、分析建模、数值模拟相辅相成的研究方法. 然而, 复合材料组分及结构的复杂化, 给复合材料的性能预测、优化设计、成型制造等提出了新问题. 例如, 复合材料的多尺度力学性能表征、精准的反向结构设计、复合材料的不确定性传播等问题, 在传统的实验分析、理论建模、拓扑优化等框架下无法得到很好的解决. 实验观测不足、理论模型缺乏、数值分析受限、结果验证困难等传统研究手段的困境, 严重制约着复合材料研究面向未来应用的快速发展.
21世纪以来, 随着大数据的逐渐普及, 计算机算力的不断提升, 深度学习、强化学习等人工智能技术迅猛发展, 相关算法相继被应用到多个学科研究领域. 人工智能方法的优势是不再关心问题的具体物理机理, 直接由数据驱动, 因此无需建立复杂的物理模型, 也无需繁冗的经验参数, 实现了由传统的因果机理探寻向人工智能支撑下变量关系建立的转变. 人工智能作为一种技术方法, 在复合材料领域也呈现出广阔的应用前景: (1)在复合材料力学性能预测方面, 基于实验测试和数值模拟获得大量数据, 结合人工智能挖掘高维变量之间的复杂关系, 可建立由参数到性能的快速响应; (2)在复合材料优化设计方面, 无需依赖于设计者的经验积累和灵感直觉, 设定恰当的目标函数后自动迭代更新设计策略, 实现全局最优或精准的逆向设计; (3)在复合材料制造方面, 快速探明各种制造参数对复合材料力学性能的影响, 改进制造工艺, 甚至与精密机器人系统进行协同制造, 实现大型复杂结构成型新技术. 另外, 在复合材料的健康监测方面, 关联多种传感信号与复合材料状态之间的关系, 在复杂载荷条件下完成对复合材料状态的预测和控制.
围绕着人工智能赋能复合材料研究的前沿领域, 本综述的内容组成为: 第2节概括人工智能在复合材料研究中的应用步骤; 第3 ~ 5节分别介绍人工智能方法在复合材料性能预测、优化设计、智能制造三方面研究的应用现状; 最后, 第6节对人工智能在复合材料领域的未来研究方向进行探讨与展望. 全文内容的总括图如图1所示.
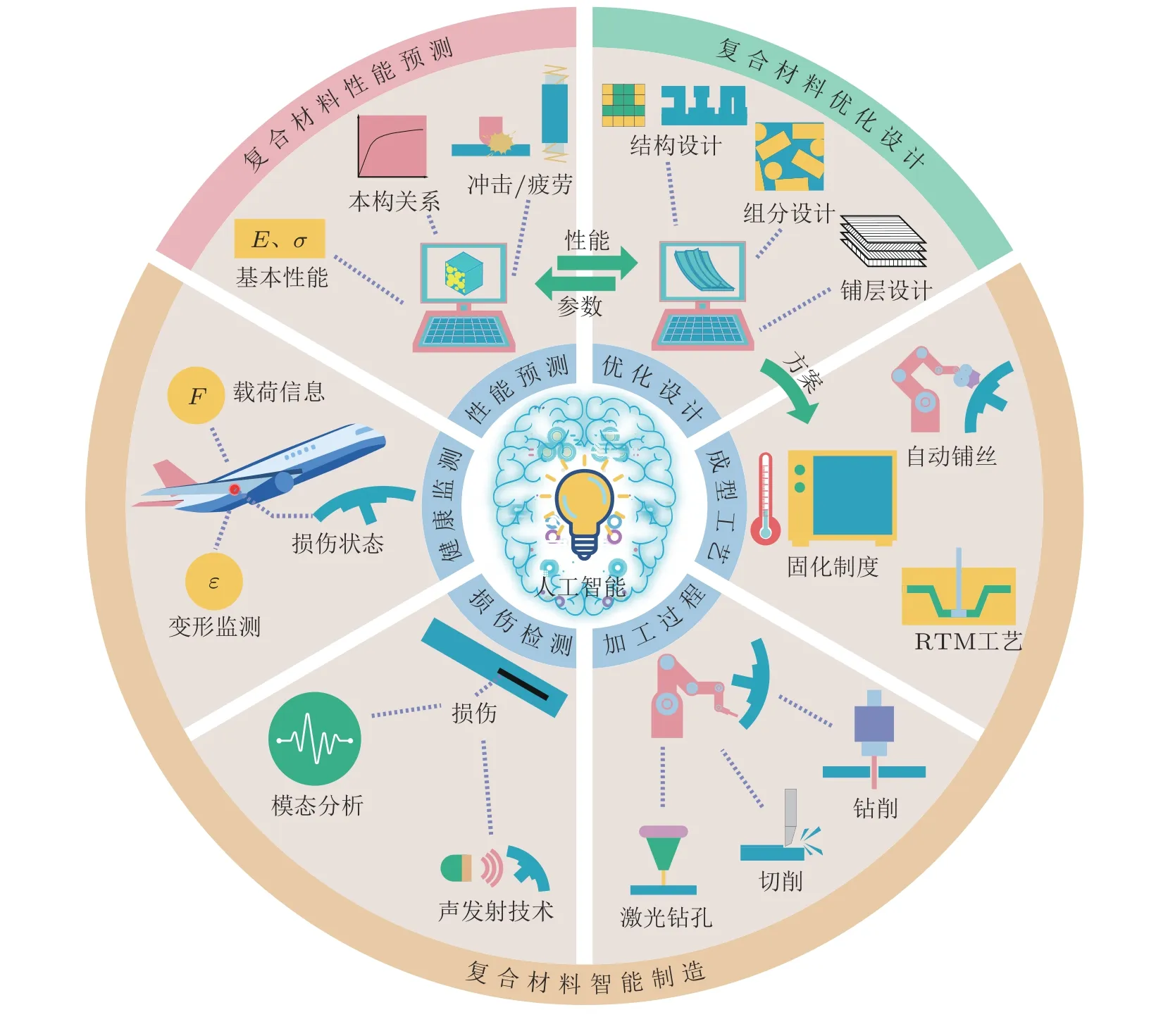
图1
2 人工智能与复合材料
2.1 材料学中人工智能应用的发展
材料是人类用以制造基本元件、构件、机器以及更复杂材料产品的物质基础. 人类社会的发展历程, 在某种程度上, 就是以材料的发展与迭代为主要标志的. 100万年前, 原始人以石头作为工具; 1万年前, 人类对石器进行加工, 使之成为器皿和精致的工具; 1千年前, 人类开始使用铸铁, 人类社会进入铁器时代; 1百年前, 人类科技得以迅猛发展, 合成高分子材料、陶瓷材料、电子材料、复合材料等新型材料的相继发明, 使人类社会从工业时代进入信息时代. 如今, 在5G和物联网时代, 材料的设计与应用也逐渐与人工智能技术建立起联系, 藉由人工智能探索其新思路、新方法、新技术. 因此, 人工智能有望为材料学发展带来新的研究范式.
自1956年“人工智能(artificial intelligence, AI)”这一学科被正式提出以来, 其发展经历了多次高潮与低谷. 2006年, Hinton和Salakhutdinov(2006)提出深度学习的概念之后, 人工智能又重新进入大众视野. 人工智能的发展历程如图2所示. 近年来, 随着计算机、大数据、互联网、物联网等先进技术的飞速发展与融合, 人工智能在计算数据、算法、算力等方面均得到了巨大提升, 如今已跨越了学科之间的鸿沟, 并在前沿科技、工程应用、医疗健康等面向未来的诸多重要领域中起着愈发关键的作用.
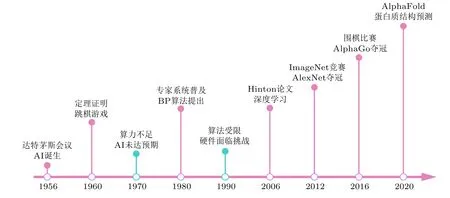
图2
当人工智能方法追溯到20世纪80年代, 专家系统(expert system)以其启发性、透明性、灵活性及扩充性等优点, 被广泛应用于材料的选择与设计. 专家系统作为一种智能计算机程序系统, 其内部含有大量的某个特定领域专家水平的知识与经验, 再进行推理和判断, 从而模拟人类专家解决问题的决策过程. 但是, 专家系统对不同情况的适应程度需由规则来决定, 而建立复杂问题的专家系统往往需要极高的时间成本和数据成本. 另外, 可移植性差、非鲁棒性、无记忆性等缺陷也严重制约着专家系统形成通用方法. 进入21世纪, 神经网络的算力瓶颈, 随着计算机硬件性能跃升而被打破, 这为基于大数据发展的人工智能方法奠定了基础. 其中, 线性回归、支持向量机、神经网络、深度学习、强化学习等方法, 逐渐被应用于材料的性能预测、设计和优化.例如, 采用机器学习方法可预测不同几何参数下多晶硅试样的断裂韧性(Liu, Athanasiou et al.2020a); 采用卷积神经网络方法, 可基于大量页岩微细观结构的图像来构建页岩微结构与弹性模量之间的关系(Li 2019); 采用强化学习方法可实现具有不同禁带声子晶体的设计(Luo C et al.2020).
2.2 复合材料领域人工智能方法
相比于各向同性或均质、单一材料而言, 复合材料在力学性能上的高度各向异性、多样性的设计参数、广阔的设计空间, 使其天然地拥有更庞大的数据量, 所以复合材料的设计与优化过程也更为复杂. 因此, 如何将人工智能方法用于复合材料研究, 以加速复合材料的设计与迭代, 促进其在工程领域的高水平应用, 是复合材料领域研究面临的重要科学问题. 目前, 人工智能方法
在复合材料研究流程可分为数据准备、模型训练、模型评估三个步骤, 如图3所示.
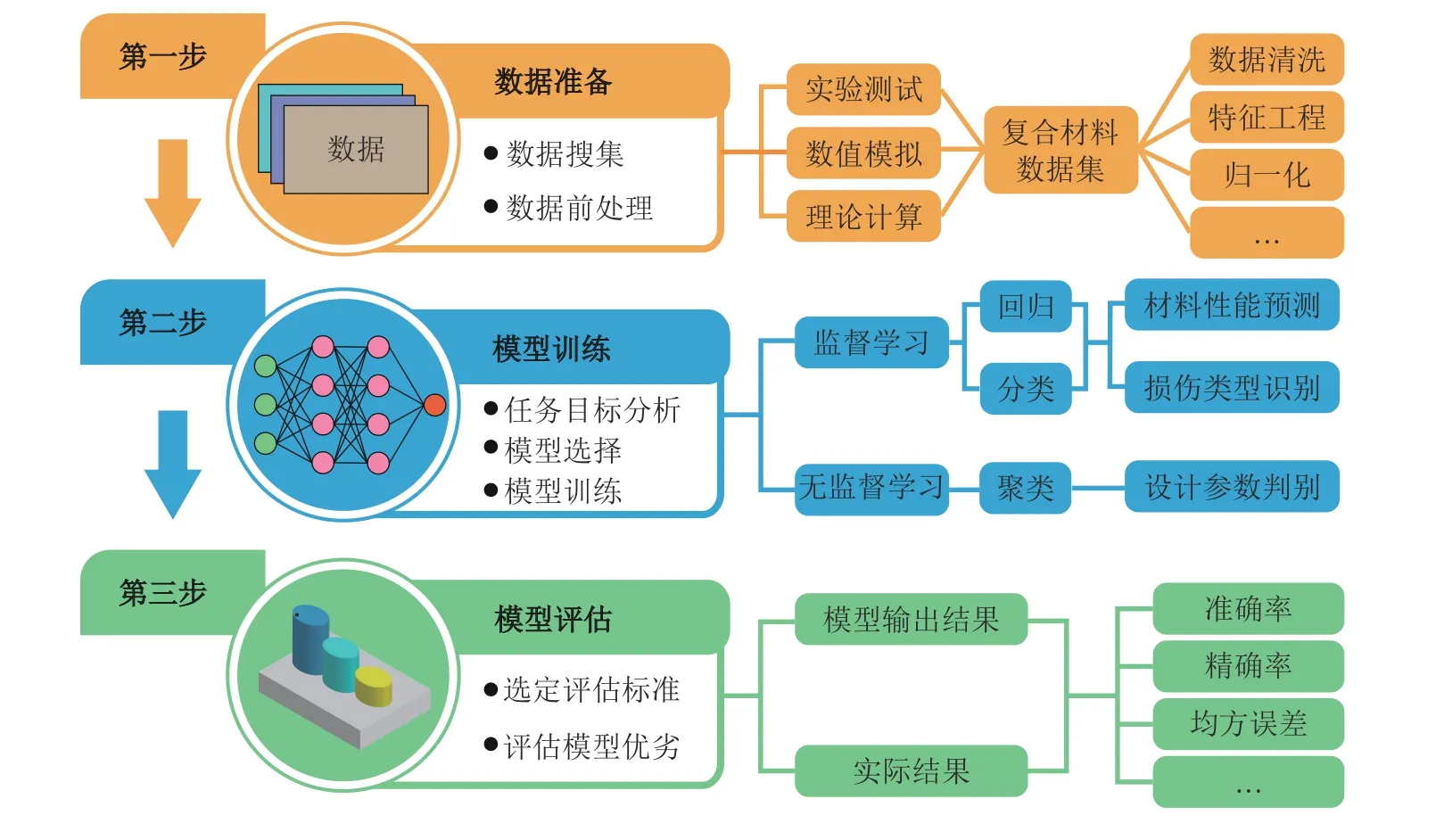
图3
2.2.1 数据准备
在复合材料领域, 原始的数据一般从数值模拟和实验中获得, 但是这些数据通常会存在信息不完整、噪声过多、数据冗余等问题. 对于信息采集中数据丢失而产生的不完整数据集, 应对缺失数据进行估算和删除. 噪声数据可以通过分箱、聚类等方法加以筛选. 在原始数据中, 有些输入变量与想获得的输出变量无关, 或与其他变量作用一致, 形成冗余数据, 可由研究者的先验知识进行选择. 例如, 在预测复合材料加筋板的屈曲载荷时, 设计参数多达十余种, 但最相关的只有四个因素: 加筋板的正交各向异性比、拉伸刚度与剪切刚度比、板与筋的拉伸刚度比以及剪切屈曲参数(Mallela et al. 2016). 因此, 在数据准备阶段对数据进行合理的预处理, 有助于提高运算效率, 提升预测精度, 获得准确的模型.
2.2.2 模型训练
确定输入与输出变量, 完成训练样本的准备后, 即开始对人工智能模型进行训练. 以目前主流的神经网络为例, 模型内部实际上是一个“黑盒子”, 在每层神经元之间使用线性或非线性的函数建立关系, 最终在输入数据及输出数据之间形成链接. 在复合材料领域, 给定的目标参数与目标性能之间往往存在着已有理论模型无法合理诠释的复杂关系, 而人工智能模型可直接基于数据进行拟合和外推, 完成“参数−性能”关系的数据挖掘. 例如, 在两相甚至多相复合材料中, 研究复杂微结构对复合材料整体力学性能的影响时, 很难找到一个理论公式准确描述不同增强相在基体中不同的分布方式与复合材料力学性能之间的关系, 但通过人工智能可实现由实验数据进行建模, 建立材料的“微结构−性能”这一连接, 供研究者了解不同材料微结构下性能的变化趋势,进而推动复合材料设计(Yang et al. 2019).
2.2.3 模型评估
完成人工智能模型训练后, 对模型效果的评估至关重要. 通过评估, 可以了解利用当前数据建立的模型是否准确, 以及当前模型在未经训练的数据集上是否拥有良好的性能, 进而选择结果更为精确、泛化能力更强的人工智能模型. 因此, 应将获得的数据集划分为两个部分−训练集与测试集, 其中训练集用于训练模型, 测试集对训练后的模型进行评估. 根据不同的数据集划分方式, 可分为留出法、K折交叉验证法以及自助法.
(1)留出法: 指按照一定比例将数据集划分为训练集与测试集, 在训练集上训练模型并在测试集上对模型进行评估. 为了保证评估的准确性, 需要尽量保持训练集与测试集的数据分布一致, 并进行若干次随机划分, 重复实验取平均值.
(2)K折交叉验证法: 指随机将样本划分成K个互斥且大小相同的子集, 以K−1个子集作为训练集训练模型, 剩余的一个子集作为测试集, 形成K种划分方式进行评估, 对所得结果取平均,是目前应用最为广泛的方法. 当K与样本数目相同时, 又被称为留一法. 该方法评估结果的可靠性随着K的增大而增大, 然而所花费的时间也随之线性增长, 因此在实际应用中选择合适的K值尤为重要.
(3)自助法: 指以自主采样为基础, 在n个样本数据中随机抽取一个并放回, 重复n次, 得到一个与样本数据大小一致的训练集, 而未出现在训练集中的数据构成测试集. 当数据样本较小,难以划分测试集与训练集时该方法简单、有效, 但自助法会更改原始数据集的分布, 从而引入估计误差.
随后, 通过将训练集得到模型的预测结果与测试集实际结果进行比较, 可以检查模型的准确性. 针对不同的问题评估方法也不同, 如分类问题一般采用准确率、精确率、召回率以及F1值,而回归问题则多为均方误差、均方根误差及平均绝对百分比误差等.
2.3 复合材料领域常用人工智能算法
在上述步骤中, 根据目标问题选择合适的模型进行训练, 是最为关键的一步. 不同的人工智能算法对应不同的应用范围, 目前还没有一种算法能够解决所有的问题(Liu et al. 2017). 目前在复合材料领域常用的人工智能算法可以大致分为三类: 回归、分类和聚类. 其中, 回归和分类作为监督学习, 多用于复合材料的性能预测(Bai et al. 2008, Jiang et al. 2008, Wen et al. 2011, Konstantopoulos et al. 2020)、损伤种类识别(Barry et al. 2015, Wang et al. 2018)、逆向设计(Kazi et al. 2020)等. 聚类用于判断损伤是否存在和复合材料关键参数识别等(Zeliff et al. 2016, Zhou et al. 2018). 此外, 以遗传算法为代表的智能计算方法也常用于优化复合材料结构设计、制造参数和人工智能模型超参数(Riche & Haftka 1993, Zheng et al. 2009, Kalantari et al. 2017, Vo-Duy et al. 2017).
神经网络(neural network, NN)是人工智能中应用最为广泛的算法, 多种神经网络在复合材料领域的分类与回归任务上表现出优异的性能. 组成神经网络的基本单位是一个个神经元, 每个神经元利用数学模型对神经细胞进行简单模拟, 一个神经元的输出作为另一个神经元的输入, 多个神经元相互连接构成了神经网络. 神经网络具有多种拓扑结构, 最简单也最为常见的是多层感知机(multilayer perceptron, MLP), 它由输入层、输出层和隐含层构成. 输入层连接输入参数, 输出层给出输出结果, 隐含层中前一层每个神经元的输出作为输入传递给下一层的每个神经元, 因此又被称为全连接层(fully connected layer). 神经网络隐含层中每个神经元采用非线性激活函数引入非线性, 具有极强的非线性拟合能力. 万能近似定理表明, 具有一个包含有限数量神经元隐藏层的神经网络可以实现任意连续函数关系的拟合(Hornik 1991). 除了多层全连接前向神经网络外, 卷积神经网络(convolutional neural networks, CNN)是另一种广泛使用的算法. 除全连接层以外, 卷积神经网络的隐含层中还包含了卷积层(convolutional layer)以及池化层(pooling layer),卷积层实现特征提取, 池化层进行特征选择和信息过滤. 与多层全连接前向神经网络相比, 卷积神经网络从信息中提取相关特征的能力更强, 计算效率更高, 在图像识别等任务上表现出更为优异的性能.
遗传算法(genetic algorithm, GA)是一种受达尔文进化论启发, 借鉴生物进化过程而提出的智能计算方法, 在复合材料的优化设计领域有着较为成熟的应用(Yuen et al. 2020). 遗传算法首先将要求解的问题编码为遗传空间中的染色体或个体, 随机产生初始群体, 根据优化目标设定适应度函数对群体中的个体进行评价. 随后, 对群体内的优胜个体进行选择, 劣质个体进行淘汰, 并进行交叉、变异运算产生新个体, 再次进行评价, 如此反复迭代直至最优个体的适应度不再上升或达到给定的迭代次数. 遗传算法的优点是具有良好的自组织、自适应和自学习能力, 搜索覆盖面大, 有利于全局择优. 其缺点是效率较低, 易出现“早熟”现象, 即过早收敛, 陷入局部最优.
在复合材料领域, 上述两种方法应用较为广泛, 并逐渐形成了遗传算法与神经网络相互结合,反复迭代, 实现复合材料的优化设计的成熟模式(Ehsani & Dalir 2019). 除此之外, 决策树、支持向量机等算法也常常被用于分类与回归问题(Wagner et al. 2019, Jac Fredo et al. 2019). 人工蜂群算法、模拟退火算法、萤火虫算法和粒子群算法等新型智能计算方法也逐渐应用于复合材料或神经网络结构的优化设计(Erdal & Sonmez 2005, Apalak et al. 2013, Vosoughi et al. 2017, Gautam &Mishra 2019). 根据目标问题合理选择人工智能模型, 有助于获得更好的预测结果(Freirejr et al.2007, Li et al. 2018).
本文按照复合材料的研发流程, 将人工智能方法在复合材料领域的应用分为三类: (1)复合材料的性能预测; (2)复合材料的优化设计; (3)复合材料的智能制造. 此外, 不仅人工智能方法可以助力复合材料研究的发展; 反过来, 力学理论作为准确模型也可以指导设计出更为符合复合材料领域需求的人工智能模型. 因此, 基于力学理论指导的人工智能方法近些年来也得到了很多力学研究者的关注.
3 复合材料性能预测
与单一均质材料相比, 复合材料由于其本身具有结构属性, 在设计时需统筹材料、结构、工艺三方面设计以达到最优性能. 同时, 复合材料可设计性强, 设计参数多, 如果缺乏设计参数对复合材料性能影响规律的清晰认识而盲目设计, 将会造成大量资源和时间的浪费. 因此, 需要对于拟设计复合材料的性能进行定量预测, 以实现根据实际需要来限制设计空间、指导设计方向, 达到高效设计高性能复合材料的目的.
目前主要采用实验研究和计算模拟两种方法实现对复合材料力学性能的预测, 但这两种方法均难以准确捕捉复合材料性能的诸多影响因素. 采用人工智能方法对复合材料性能进行预测,即通过数据挖掘微细观结构或设计参数与复合材料性能之间内在的关系, 进而对如基本力学性能、疲劳性能、冲击性能等做出预测, 或者建立材料的本构模型, 是目前针对复合材料性能研究的前沿热点.
3.1 复合材料基本力学性能
复合材料研究水平不断提升、应用领域不断拓展, 目前已逐渐被用于各类承载结构(主承力和次承力结构), 例如飞机机身机翼、汽车车身、风电叶片等关键结构. 而复合材料模量、强度、韧性等基本力学性能是影响其结构承载能力的决定性因素.
3.1.1 基于微结构图像的性能预测
复合材料的微细观结构决定其宏观力学性能. 目前复合材料多尺度力学主要通过大规模观测不同载荷下微细观结构形貌, 依据经验判断、提取关键特征, 进而建立力学模型. 该方法相对繁琐, 高度依赖研究者丰富的经验. 采用人工智能方法研究该问题, 可实现微细观结构特征的快速提取, 或直接建立“图像−性能”这一关系, 驱动复合材料多尺度力学的快速发展.
利用二维微结构像素图像来预测复合材料整体力学性能的方法. Gu 等 (2018a)采用计算机生成35 960张8 × 8像素单位的两相夹杂复合材料二维图像, 结合有限元分析得到的韧性和强度训练卷积神经网络, 实现由二维结构图像预测材料的韧性和强度, 成功挖掘了结构图像与材料性能的定量关系, 且计算速度约为有限元方法的250倍. 针对具有任意形状夹杂相分布的二维复合材料微结构, Ye等(2019)在200 × 200像素单位图像上进行分析并建立卷积神经网络, 可预测复合材料的等效杨氏模量以及泊松比, 预测结果相对误差均低于4.0%. 另外, 针对纤维增强复合材料,可将纤维增强体视为夹杂相分布于树脂基体中. 利用计算机生成的1800张碳纤维增强复合材料单向板的二维横截面微观结构图, 通过有限元施加周期性边界计算出其弹性模量和屈服强度, 再采用梯度上升回归树方法将结果与复合材料微观结构相关联, 获得了不超过5%的预测误差(Pathan et al. 2019). 除力学性能外, 类似的方法在预测复合材料有效导热系数和导电率上也取得了良好的效果(Turias et al. 2005, Gerrard et al. 2014).
上述研究均是针对二维复合材料微结构, 或将三维问题简化至二维平面问题. 但实际应用中往往以三维复合材料为主, 一些复合材料(如具有不同角度铺层的复合材料、三维编织复合材料)微结构也难以简化至二维问题. 仅仅采用二维图像进行研究存在一定的局限性, 因此需要对复合材料三维微结构进行建模研究. 基于三维微结构图像的复合材料性能预测方法如图4所示.将计算机随机生成图像结合三维高斯滤波, Yang 等(2018)首先创建了8550个三维体素化复合材料微观结构, 再以三维微结构模型作为输入, 有限元计算得到的有效刚度作为输出训练卷积神经网络, 建立了三维微结构与有效刚度的内在关系. 相较于复杂的受物理启发方法, 该方法预测结果平均绝对误差减小了54%. Xu Y 等(2015)未直接建立复合材料三维微观结构, 而是根据三维编织复合材料的微观结构, 提取了纤维尺度与丝束尺度的关键几何参数, 利用人工神经网络构建微观结构参数和拉伸模量之间的非线性映射关系. 该方法预测值与实验结果的误差均小于10%, 且无需构建超参数相对复杂的卷积神经网络, 但如何准确选择微观结构的关键参数, 仍依赖于研究者的经验积累.
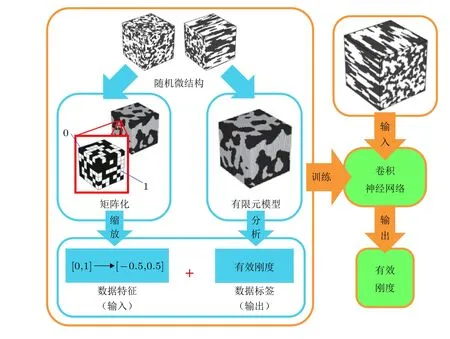
图4
复合材料二维微结构图像会损失实际三维模型的信息, 因此采用三维模型与实际材料结构更相符. 但使用三维微结构训练卷积神经网络耗费的计算资源会随着模型精细程度成倍增长, 不利于实现对复合材料微观结构的精确分析. 因此, 在三维微结构中选取多个适当的二维剖面作为输入, 在某些复合材料结构性能的预测中具有优势. 如图5所示, Rong等(2019)选取三维微结构x和y方向的等距二维剖面作为输入, 构建二维卷积神经网络预测复合材料的有效导热系数. 结果表明, 相较于输入整个三维结构, 以多个适当的二维剖面作为输入更加高效、精确, 其平均绝对误差与均方根误差分别为2.5%与3.1%. 该方法降低了基于复合材料三维微观模型进行性能预测时所需的计算量, 对具有较大计算量的复合材料结构(如复合材料精细三维模型、无法采用代表性体积元计算的复合材料等)的性能预测提供了新方法.
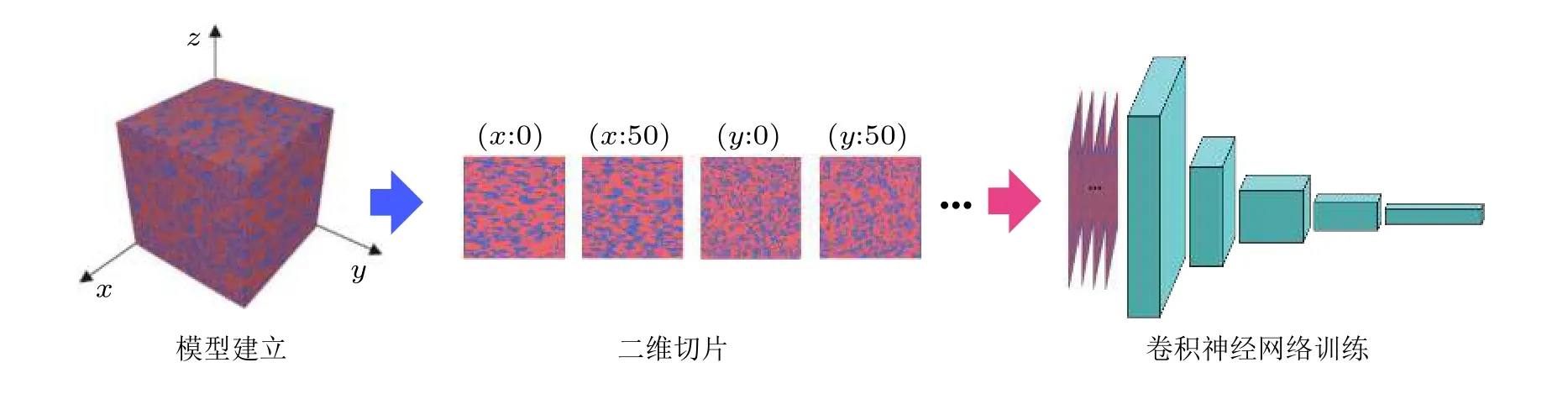
图5
3.1.2 基于复合材料设计参数的性能预测
利用复合材料微结构图像可有效预测复合材料力学性能, 但是, 工程应用中复合材料微结构图像的获取有时是非常困难的, 而利用复合材料的设计参数来预测其力学性能则相对容易, 如纤维增强复合材料中纤维的种类、铺层的角度、设计结构的布置, 颗粒/纳米增强复合材料中填料的形态、大小等. 因此, 采用人工智能方法建立“设计参数−复合材料结构−性能”的快速响应, 为进一步开展复合材料优化设计、加速复合材料研发进程奠定基础.
对于连续纤维增强复合材料而言, 纤维、基体的种类和含量以及铺层的数目和顺序是影响力学性能的关键设计参数. Bezerra等(2007)采用人工神经网络预测了碳纤维增强环氧复合材料和玻璃纤维增强环氧复合材料在不同铺层顺序下的剪切力学性能. Khan S M等(2019)以碳纤维、玻璃纤维作为增强纤维, 聚苯硫醚、高密度聚乙烯作为基体制备了四类复合材料, 并分别测定了不同铺层数目下复合材料的硬度、悬臂梁冲击强度以及横向断裂/抗弯强度, 利用人工神经网络通过铺层数量以及纤维、基体的种类预测上述力学性能, 其平均绝对误差均小于5%, 证明人工神经网络在复杂变量下仍能保持良好的预测稳定性. Barbosa等(2020)利用人工神经网络对不同铺层数目和铺层角度的复合材料ABD矩阵本征值进行了预测. 另外, 工程中广泛运用的复合材料加筋板的屈曲性能与正交各向异性比、拉伸刚度与剪切刚度比、板与筋的拉伸刚度比以及剪切屈曲参数密切相关, 这些参数作为神经网络的输入可以达到预测屈曲性能的目的(Mallela &Upadhyay, 2016). 其平均预测误差仅为2%, 而计算速度可达有限元方法的数百倍, 大幅提升了复合材料加筋板设计中对结构承载能力进行评估的效率.
类似研究也已在颗粒增强复合材料以及纳米复合材料之中展开. 采用人工神经网络方法, 可通过基体材料、填料材料、填料重量百分比、填料直径以及填料长宽比对纳米复合材料相对杨氏模量进行预测, 误差仅为5.06% (Cupertino et al. 2011). Daghigh等(2020)则应用AdaBoost以及回归树方法挖掘了颗粒增强复合材料中, 不同颗粒填充物与复合材料的断裂韧性的内在关系.还有一些研究通过基因规划方法预测了材料的性能, 同样呈现出良好的可靠性(Pouraliakbar et al.2014, Sabouhi et al. 2015). 除了准确、高效外, 人工智能方法还能捕捉到现有理论模型未能发现的内在关联, 弥补理论模型的不足. 例如在铜粉/聚乙烯复合材料中, 当铜粉含量大于2%时, 现有理论模型均无法计算不同铜粉含量下的断裂延伸率、破坏应力和杨氏模量, 而人工神经网络则可以由实验数据准确预测(Bhoopal et al. 2015).
复合材料在实际制造生产过程中往往具有一定的分散性与随机性, 导致实际参数和材料性能等与设计时并不一致(António & Hoffbauer 2010). 若忽视这一现象, 会使复合材料的实际力学性能偏离设计目标. António和Hoffbauer (2013)将人工神经网络和蒙特卡罗模拟方法相结合, 研究了复合材料纵向、横向弹性模量和拉伸、剪切强度的不确定性对可靠性指标的影响. 结果表明, 复合材料基本力学性能的微小不确定性可能在可靠性指标中放大, 不利于安全可靠的复合材料设计制造. 因此, 在采用设计参数预测复合材料的性能时, 有必要将设计参数和材料性能的不确定性纳入考虑. 如复合材料模压成型工艺中随机纤维取向对力学性能影响显著, 是预测模压成型复合材料性能时需要考虑的关键不确定性因素. Sabiston等(2020)对模压成型复合材料选定数个位置作为样本进行CT扫描得到断面图像, 并对图像中的纤维取向采用二阶张量进行表征,构建人工神经网络由位置坐标预测纤维取向张量. 训练后的人工神经网络可对模压成型复合材料不同位置的纤维取向张量实现快速、精确的预测, 为未来实现模压成型复合材料力学性能的精准判断奠定了基础.
3.2 复合材料本构关系
复合材料的本构关系和损伤失效模型可由基本的物理定律和假设导出, 理论上不存在不确定性. 然而实际中往往是基于实验数据对材料状态进行假设, 选取多个经验函数不断修正, 构建经验模型. 随着复合材料的组成和结构日趋复杂, 非线性力学行为也更加复杂, 可能存在多种失效机制, 但现有力学模型难以同时体现这些机制的共同作用. 采用人工智能方法则直接由复合材料的设计参数和测得的应力应变曲线作为数据, 构建不同材料参数下应力与应变的关系, 无需考虑复合材料内部复杂的机理, 也避免了经验建模带来的误差.
Pidapart和Palakal (1993)以纤维铺放角度、初始应力以及应力增量作为输入, 总应变作为输出训练了人工神经网络, 成功构建了不同铺层角度下的单向层合板的应力−应变曲线, 提供了复合材料本构建模的新方法. Ghaboussi等(1998)提出一种自动渐进训练的人工神经网络训练方法, 预测了复合材料不同应变下的应力响应, 与解析解十分吻合, 进一步提升了预测的精确性.Yang C等(2020)基于卷积神经网络预测了两相夹杂复合材料的超出弹性极限的应力应变曲线,预测结果与实际曲线吻合较好, 平均绝对误差均在10%以内.
人工智能方法可以由实验数据直接建立本构模型, 减少复杂的理论分析, 加速力学模型在工程上的应用. 反之, 也可根据力学理论挑选人工智能的建模参数, 减少干扰变量、冗余变量, 甚至基于力学约束改写损失函数、优化算法, 提升人工智能模型训练效率, 增强对未知数据的解释能力, 实现力学理论对人工智能方法的指导.
通过构建多个的神经网络逐步分析, 可以在每一步中引入相关的理论模型进行串联, 达到校准模型参数, 构建复杂模型的目的. 基于多级相连人工神经网络构建的准各向同性复合材料层合板的渐进损伤模型, Zobeiry等(2020)获得了与实验结果高度重合的载荷−POD (pin opening displacement)曲线. 通常的神经网络系统均是以直接测量数据作为输入与输出, 而将神经网络与力学模型相连, 并改写反向传播(back propagation, BP)算法, 可以实现由间接测量数据构建本构模型(Liu, Tao et al. 2020). 该系统如图6所示, 多个共享权重与偏差的神经网络构成一个子系统,并将神经网络的输入(ik)与输出(ok)通过其他力学模型子系统(如由经典层合板理论推导出的运动学、动力学方程), 与可测量的输入(Is)与输出(Os)相连接, 成功学习了复合材料非线性面内剪切本构方程以及失效起始准则, 与相应理论分析结果具有良好的一致性. Liu 等(Liu & Wu 2019, Liu Z et al. 2019, Liu 2020)将连续介质力学、代表性体积元和均匀化理论等与神经网络方法相结合, 由力学模型组成神经元, 构建了深度材料网络. 该方法弥补了普通神经网络无法引入物理约束的缺陷, 在二维和三维材料结构上均展现出良好的预测性能. Yang H等(2020)基于模拟得到的不同加载路径下的平均应力−应变数据, 采用人工神经网络方法训练得到屈服函数(yielding function), 成功描述了微结构材料的弹塑性本构关系. 动力学目前以常微分方程为桥梁,构建了神经网络常微分方程, 在动力系统的学习上展现了一定的潜力(Chen et al. 2018). 上述研究则为固体力学与神经网络的结合提供了多种可能. 神经网络不再单纯是数据处理的工具, 而是更加紧密地与力学模型进行结合, 由神经网络挖掘数据关系, 力学理论施加物理约束, 为材料多尺度力学行为的高效、高保真模拟开辟了崭新的途径.
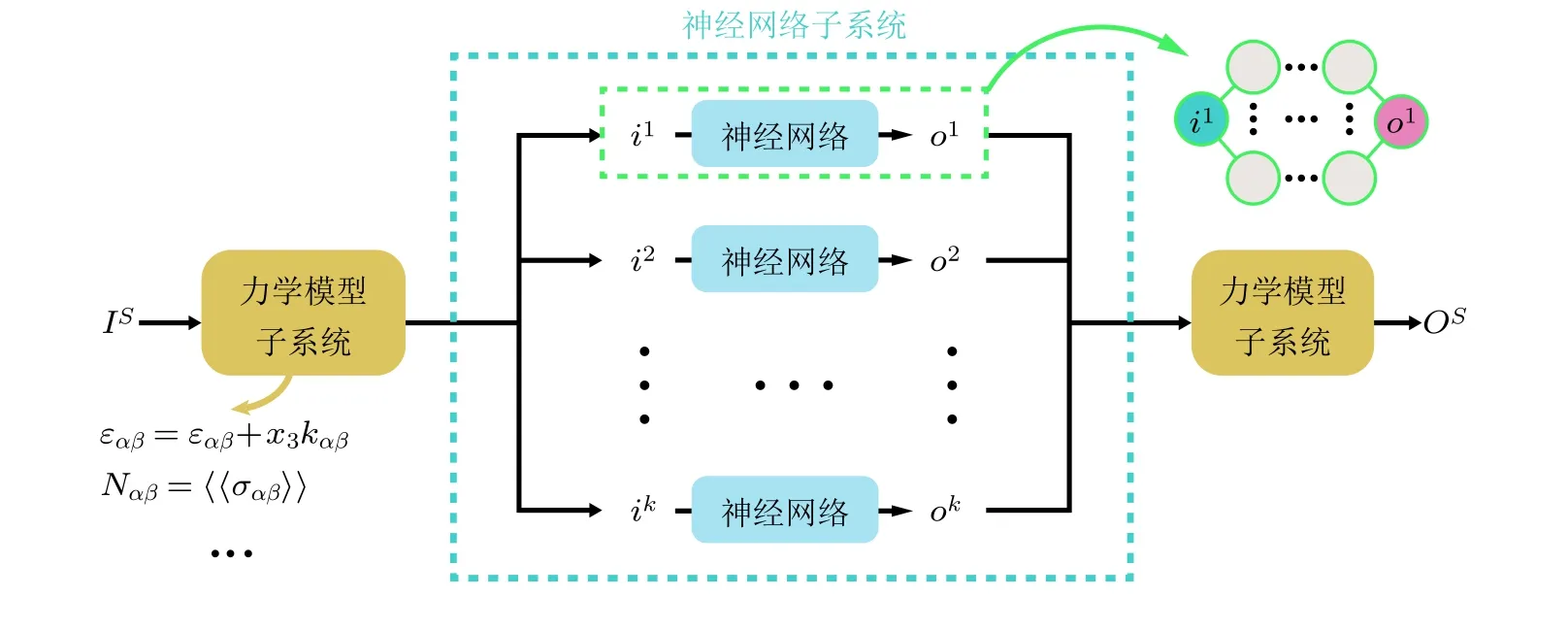
图6
3.3 复合材料冲击性能
复合材料在制备、装配和服役期间, 往往会受到多种意外载荷的冲击, 其中较低速度的冲击会对复合材料造成不可见、不可恢复的损伤, 使复合材料结构力学性能下降. 高速度的冲击会直接造成复合材料结构的破坏, 形成重大安全事故. 目前, 复合材料在冲击载荷作用下的损伤建模及材料性能折减关系仍是研究的热点与难点. 采用人工智能方法实现对复合材料在承受冲击载荷后响应的高效精确分析, 有利于准确评估复合材料结构的安全性、可靠性, 也有利于探索冲击载荷下复合材料损伤规律, 从而实现耐冲击复合材料设计.
目前已有部分研究者将人工智能方法应用于复合材料的低速和高速冲击研究. Chandrashekhara等(1998)最先采用人工神经网络研究了低速冲击中复合材料层合板的接触力. Addona等(2012)根据实验数据, 采用人工神经网络预测了玻璃纤维增强复合材料层合板在承受不同程度低速冲击损伤后的剩余拉伸强度. Laban等(2020)采用人工神经网络, 通过初始峰值力、平均载荷及压碎力效率, 预测了受低速冲击载荷后复合材料圆管的准静态压缩承载能力, 成功对该高度非线性行为进行建模, 均方差仅为0.191 N. Fernández-Fdz等(2008)将实验、有限元和人工神经网络三者结合, 针对复合材料的高速冲击问题, 预测了在不同的冲击角度和冲击速度下, 复合材料是否被穿透, 以及未被穿透情况下的损伤区域面积和被穿透情况下的剩余角度和剩余速度.结果表明, 人工神经网络的各项预测结果与实际数据的误差均在7%以内. Artero-Guerrero等(2018)同样基于如图7所示的“实验−有限元分析−人工神经网络”这一范式, 预测了复合材料在不同铺层顺序下的弹道极限(ballistic limit). 人工神经网络的预测结果在训练集和测试集上的误差分别为3.7%与7%. 基于所建立人工神经网络的准确预测, 归纳得出在复合材料受冲击侧布置0°和90°铺层有助于提高复合材料层合板的弹道极限, 实现了对复合材料设计的指导.
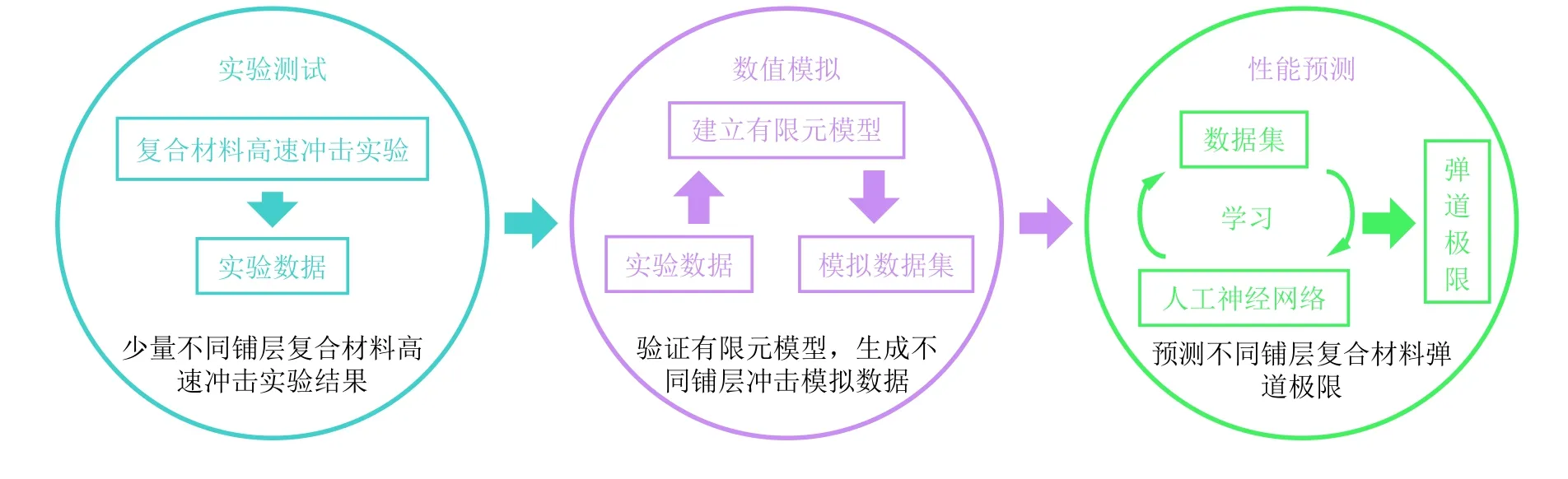
图7
3.4 复合材料疲劳性能
由于复合材料具有疲劳损伤模式的多样性和扩展的不规律性, 传统损伤模型的适用性较差,因此复合材料疲劳性能的确定往往依赖于大量的实验. 人工智能方法为复合材料疲劳行为的模型建立提供了新途径, 即直接预测复合材料的疲劳性能, 而无需关注复合材料疲劳破坏的复杂机理. 因此, 采用人工智能方法预测复合材料的疲劳性能将是一种有效的新思路.
Aymerich和Serra (1997)率先采用了人工神经网络, 研究了不同循环周期下复合材料铺层顺序对疲劳强度的影响, 但高周疲劳的误差较大. 随后, Lee 等(1999)除了考虑复合材料的拉伸强度、压缩强度、拉伸破坏应变及拉伸模量外, 还选取了峰值应力、失效概率等疲劳试验参数建立人工神经网络预测疲劳寿命, 预测准确度有了显著提升. Vassilopoulos等(2006)依照同样的思路, 通过实验得到数据集, 建立人工神经网络预测玻璃纤维增强复合材料的疲劳寿命. El Kadi团队(El Kadi 2008; Al-Assadi et al. 2009, 2010)则对人工智能方法复合材料单向板的疲劳寿命预测上展开了广泛研究, 考虑了纤维取向、纤维类型等对复合材料疲劳寿命的影响, 还进一步评估了不同人工智能方法的性能. 上述研究均是基于“点对点”问题出发, 即以给定的一系列输入物理量预测输出物理量的值, 而复合材料的疲劳损伤则是一个与时间序列密切相关的问题. 因此, Tao等(2021)使用神经网络常微分方程与β变量自动编码器(β-variational autoencoder)对纤维增强复合材料的刚度退化行为进行建模, 并给出了相应的S-N曲线, 其预测效果显著优于现象学模型, 而无需建立复杂的力学模型. 目前的研究主要集中在恒定幅值载荷的疲劳寿命预测上, 面对更为复杂的变幅值载荷疲劳问题, 如何准确提取关键特征进行时间连续的疲劳寿命预测, 仍需进一步进行研究.
3.5 小结
综上所述, 目前将人工智能应用于复合材料性能预测的主要方法是通过实验或数值模拟收集数据, 运用人工智能方法辅助力学模型建立, 或直接通过数据构建模型, 在验证人工智能模型可靠性后进行性能预测. 因此, 采用人工智能方法实现复合材料性能预测时无需建立复杂的经验模型, 也不存在经验建模的误差, 模型的预测准确程度主要受数据集影响. 想要获得能够准确预测材料性能的模型, 势必要提供大量的数据, 而这又将带来计算量的巨大提升. 人工智能方法将传统的建模问题转变为数据搜集以及数据处理的问题, 在预测复合材料性能中面临的主要挑战有: (1)高精度人工智能模型的建立需要大量的数据, 对复合材料实验数据库的构建提出了要求;(2)在海量的数据中提取到最为关键的特征参数以减小计算量; (3)量化所建立模型中参数的不确定性及其影响; (4)由人工智能模型预测规律实现对相应力学模型的构建; (5)在人工智能模型构建过程中合理引入力学模型, 施加物理约束, 实现力学理论对人工智能方法的指导.
4 复合材料优化设计
材料设计通常是指依据积累的经验、归纳的实验规律以及总结的科学原理, 来制备具有确定目标性能的材料. 传统的材料设计是依赖大量实验的不断试错、大面积筛选的方法. 相比于各向同性或均质、单一材料, 复合材料的设计空间更为广阔, 力学机理更为复杂, 目前尚不能摆脱经验设计方法. 而采用反复实验的方法进行设计需要消耗大量的人力、物力以及时间成本, 且最终优化设计得到的结果也未必是最优解. 在这种条件下, 研究者们开始应用计算机技术辅助复合材料的设计, 以降低实验成本, 减少设计时间. 如今, 随着数值模拟技术的成熟以及人工智能技术的不断发展, 使得计算机代替研究者进行模拟实验、探索设计空间成为了现实, 为实现复合材料准确、高效的优化设计, 提供了有效的途径和崭新的思路.
4.1 纤维增强复合材料的优化设计
纤维增强复合材料以其轻质高强的特点被广泛用于航空航天、汽车船舶等重要领域. 以纤维复合材料在航空工业上的应用为例, 波音787客机上对于复合材料的使用已经占据其结构总重量的50%, 使其结构减重超过25% (杨乃宾 2008). 为进一步发挥复合材料力学性能上的优势,提升复合材料的竞争力, 需要在维持复合材料承载能力的同时, 尽可能减小复合材料结构件的重量以及制造成本. 因此, 复合材料的优化设计一直是复合材料研究的重要领域. 20世纪90年代,研究者们将专家系统引入复合材料领域, 针对复合材料的选材与设计等问题展开了系列研究(Choi & Lee 1995, Lee & Liebowitz 1995, Jeon et al. 2002). 但专家系统只能考虑一定的范围, 学习能力较差, 依赖领域专家的先验知识, 限制了其进一步的发展. 与此同时, 遗传算法、模拟退火、粒子群优化等智能计算方法的研究日趋成熟, 成为求解复杂问题系统的有效方法. 研究者们基于一定的设计规则, 利用智能计算方法求解了简单载荷下复合材料层合板的铺层优化问题, 证明了该方法相对人工设计更为准确、高效(Ball et al. 1993, Sargent et al. 1995). Kim 等 (2005)和Kim(2007)则将专家系统与遗传算法相结合, 开发了针对较为复杂约束条件下复合材料层合板的铺层优化系统, 提升了专家系统学习与设计的效率. 随着有限元方法的不断发展, 对复杂问题的求解能力逐渐增强, 将有限元与智能计算方法相结合, 使具有复杂几何构型和复杂承载条件的复合材料优化成为可能. 例如, Herencia等(2007)以强度和屈曲载荷为约束优化了T型加筋板的铺层, Lopes 等 (2009a, 2009b)采用非标准铺层对受冲击载荷的层合板进行了优化设计, Wang 等(2016)考虑了应力约束、变形约束、屈曲约束、铺层约束和可制造性对复合材料风力涡轮机叶片进行了优化, 使得重量降低17.4%. 此外, 在使用智能计算时, 预先采用如K近邻算法、朴素贝叶斯、随机森林和决策树等分类算法对设计变量进行了分类, 筛选关键设计变量, 可以大幅减少计算量而仍保持良好的帕累托边界(Pareto frontier)(Zeliff et al. 2016).
有限元方法与智能计算方法的结合, 实现了利用计算机自主探索复合材料设计空间. 但相较于智能计算方法的快速响应, 有限元通常需要耗费大量计算时间, 阻碍了计算机自主设计速度的进一步提升. 对于一些经典力学问题, 可以通过采用理论计算而非有限元的方法来节省计算时间. 将经典层合板理论与智能计算方法进行结合, 可以实现针对复合材料强度问题的多目标优化, 减少复合材料的重量和制造成本(Omkar et al. 2011, António 2014). Pelaez等(2017)基于双轴拉伸载荷下复合材料层合板强度问题的解析解, 运用文化基因算法进行了纤维、基体的选择以及铺层顺序的优化. Kamarian等(2018)利用Mori-Tanaka方法、广义微分求积法计算了八层对称铺层矩形层合板的固有频率, 结合萤火虫算法对铺层顺序进行了优化, 得到了最大固有频率的铺层设计. 优化结果表明, 萤火虫算法虽然会损失少量计算精度, 但设计效率可提升上百倍.Wagner等(2019)以理想/非理想屈曲载荷下的单边界摄动法分析得到的数据为基础, 训练决策树模型得到一般性的设计建议, 并优化了层合板的铺层顺序. 与传统优化方法得到的层合板相比, 该方法设计的层合板具有更高屈曲载荷以及更低的缺陷敏感度.
上述研究均针对简单载荷或简单构型下的复合材料展开, 因此理论计算取得了较好的效果.但对于复杂的复合材料结构或缺乏理论解的受载情况, 上述方法则难以应用. 受神经网络在复合材料性能预测上应用的启发, 一些研究者使用已成功训练的神经网络对材料性能进行快速预测,逐渐形成如图8所示的神经网络与智能计算相结合的优化设计方法, 大幅提升了优化问题的计算效率. Jayatheertha等(1996)训练人工神经网络代替有限元方法, 与模拟退火算法相结合, 对在刚度与强度约束下层合板的铺层顺序进行了优化. Zhang 等(2008)通过人工神经网络, 由复合材料的最大应力预测其强度特性, 再进一步使用遗传算法对2.5维编织复合材料的包缠纤维密度及填充纤维密度进行了优化, 实现了复合材料的减重设计. Szklarek等(2020)采用人工神经网络与遗传算法相结合的方式, 对复合材料U型板的铺层顺序进行了优化, 提升了临界屈曲载荷.Bisagni 和 Lanzi (2002)针对复合材料的后屈曲优化问题, 训练人工神经网络取代非线性有限元分析, 采用遗传算法优化复合材料板的铺层、加强筋铺层、加强筋数量及加强筋形状四个设计变量, 使复合材料加筋板的重量减少约18%. 此外, 他们还对复合材料圆柱壳、三维编织复合材料加筋板的后屈曲问题进行了优化设计, 提升了结构的最大屈曲载荷和刚度(Fu X et al. 2015,Pitton et al. 2019).
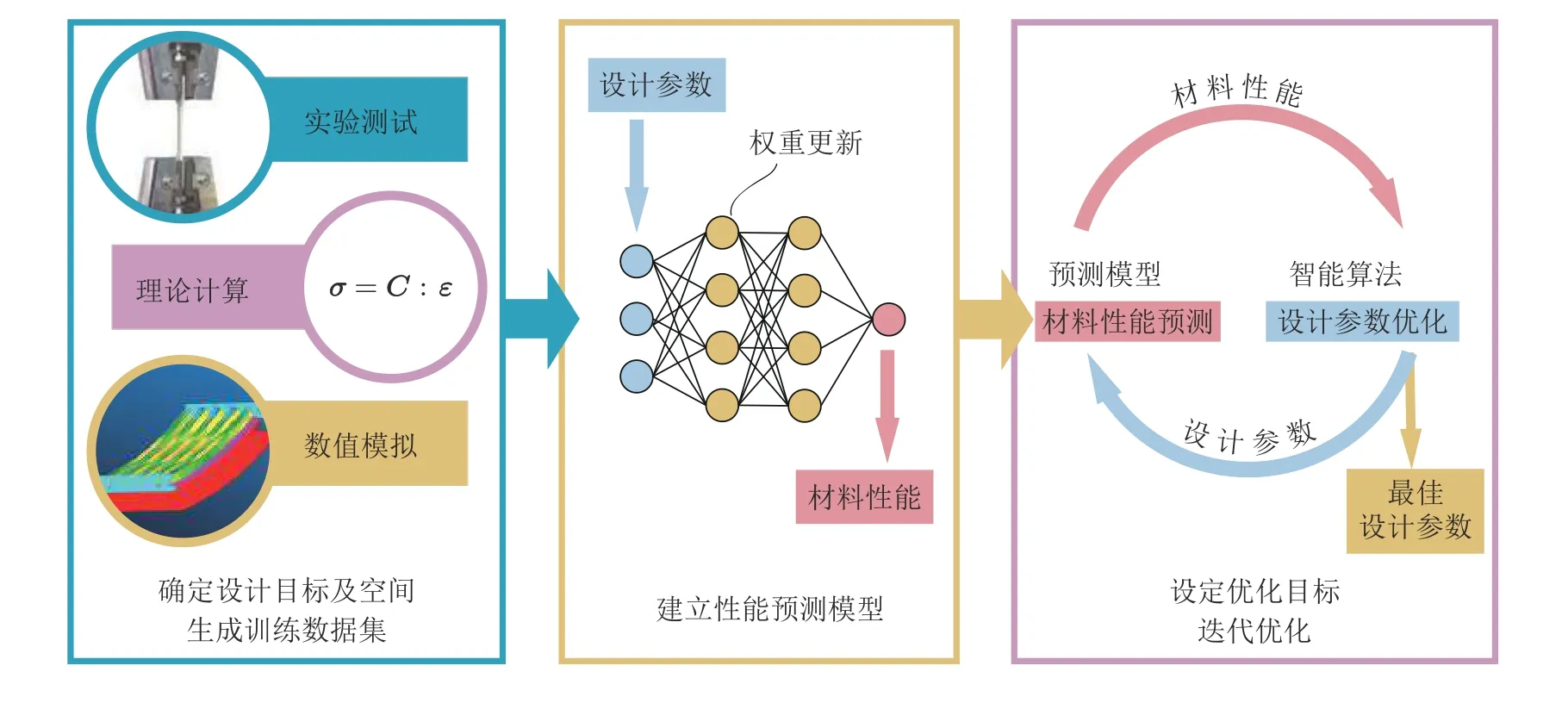
图8
无论是采用有限元或其他计算方法, 目前纤维增强复合材料的主要设计思路可以概括如下:首先, 根据设计参数, 计算得到复合材料的性能; 其次, 基于复合材料性能的计算结果, 采用智能算法更新设计参数, 探索设计空间. 而后不断迭代, 直至复合材料性能无法提升. 而与上述思路不同, Kazi等(2020)基于实验测得的不同短切棉纤维含量下复合材料性能的数据, 选定八个力学性能指标, 利用人工神经网络反向建立了性能−纤维含量之间的关系, 直接求出目标力学性能下的纤维含量. 该方法与采用材料的设计参数预测性能类似, 均为通过人工神经网络直接建立二者之间的联系, 再进一步进行预测. 通过设计参数预测材料性能为“多对一”的问题, 而指定的性能却未必只有一种设计方案, 且在数据搜集阶段, 仍需要大量探索设计空间. 该方法为快速设计的实现提供了新的思路, 但在材料优化设计方面的应用仍需进一步的研究与评估. 生成对抗网络(generative adversarial networks, GAN)和强化学习(reinforcement learning, RL)近些年来在生成建模中取得了令人瞩目的成绩, 其探索、博弈、优化的核心思想与材料的优化设计不谋而合, 并已成功应用在一些简单的材料设计中. 例如, Luo C 等(2020)采用强化学习设计了基于给定禁带的一维声学超材料, Mao等(2020)利用GAN获得了接近Hashin上界的数百种二维周期性胞元,同时满足了给定的晶体对称性和体积分数. 此外, 二者互相结合的生成对抗模仿学习(generative adversarial imitation learning, GAIL)在生成、设计领域也展现出巨大的潜力. 在更为复杂的复合材料优化设计中, 上述方法均面临着计算量大幅提升的挑战. 尤其是在不断试错中习得规律的强化学习, 对复合材料性能高效率、高保真的计算有着迫切的需求. Kalita等(2019)分别采用多目标遗传算法和粒子群优化算法与遗传编程方法相结合实现符号回归, 对复合材料层合板的自由振动问题进行了多尺度的优化设计. 该方法可以针对计算密集型问题快速生成精确的多尺度优化设计结果, 为将来进行多尺度优化设计, 更全面、更广泛地探索设计空间提供了可能.
4.2 颗粒/纳米复合材料的优化设计
与纤维增强复合材料类似, 材料性能计算与智能优化算法相结合的方法在颗粒复合材料和纳米复合材料的优化设计中也被被广泛应用. 不同于纤维增强复合材料常使用宏观参数进行优化, 由于颗粒/纳米复合材料的微结构能够表征其整体的力学性能, 许多研究者从微结构入手, 对颗粒/纳米复合材料的微观参数进行了优化设计. Gu等(2018b)利用卷积神经网络由微观图像预测两相夹杂复合材料的断裂韧性, 并结合自学习方法, 在两相夹杂复合材料的设计空间中不断寻找设计参数, 进行性能排序后筛选出最佳韧性的设计方法. Vinoth和Datta(2019)构建了人工神经网络, 通过七个纳米填料的几何参数预测了超高分子量聚乙烯基纳米复合材料的弹性模量以及极限拉伸强度, 并采用遗传算法对几何参数进行了多目标优化, 获得了更高的材料性能.
在对复合材料的微结构进行优化设计时, 关键的研究问题之一是如何获取一组数量足够小但充分详细的设计参数来确定设计空间. 若选取参数无法描述一个完整的设计空间, 那么势必会造成设计方案的遗漏, 难以达到最优设计的目的. 反之, 大量的设计参数可以详细描述设计空间,但会造成智能优化的运算量过大, 不利于求解. Xu H 等(2015)针对这一问题, 基于Relief监督学习算法建立微结构参数与材料性能的关系, 对大量用于确定纳米复合材料微结构参数进行反复筛选, 最终确定为一小组描述符, 并运用试验设计/元模型方法进行优化设计验证, 得到的设计结果显著优于未筛选设计参数得到的结果. 最近, Chen和Gu (2020)构建了一种逆设计生成网络(图9)实现复合材料的微结构优化. 该网络由两个人工神经网络构成, 分别称为预测神经网络与设计神经网络. 前者通过数据训练预测复合材料的性能, 后者则共享前者的权重矩阵, 在反向传播阶段不再更新权重矩阵, 而是逆向输出复合材料的设计方案. 他们以两相夹杂复合材料的I型断裂韧性为例, 将该方法与遗传算法及拓扑优化进行了对比, 证明了这种新型的算法可以得到更高的I型断裂韧性. 随着对神经网络的可迁移性研究的不断深入, 这种方法有望在训练完成后进行对相似优化设计问题进行快速解决, 而无需如遗传算法、模拟退火算法、群智能算法等智能优化算法耗费大量时间与计算资源探索设计空间, 为基于高维度高通量数据的智能优化设计提供了可行的方案.
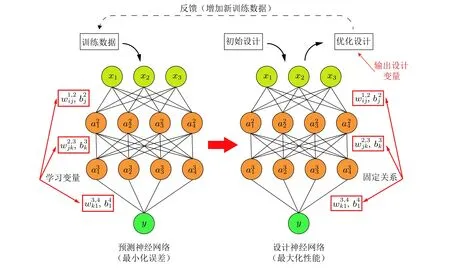
图9
4.3 小结
基于人工智能实现快速性能预测, 并结合智能计算方法自动寻优的方法在复合材料设计、优化领域被越来越多的研究者关注. 这种方法根据不同设计参数对材料性能的影响寻求优化路径, 有的放矢, 避免了大量实验资源和人力资源的投入. 与复合材料性能预测所面临的的问题类似, 建立人工智能实现复合材料优化设计的核心在于前期构建材料性能数据集的有效性. 复合材料多尺度的内部结构特征复杂, 可供选择的设计参数广泛, 如何从数据中排除冗余特征, 寻找与优化设计目标最为相关的设计参数, 准确量化模型中的不确定性以及其影响, 以实现高效、准确的优化设计模型的构建, 成为这一方法面临的主要挑战. 此外, 人工智能方法在样本数据覆盖的空间中具有较高的预测准确率, 但其是否具有良好的外推性能仍需加以验证, 因此在构建数据集时应保证数据信息尽可能的覆盖目标设计空间. 最近, 生成对抗网络在模型生成中取得成功应用, 深度强化学习在组合优化问题上崭露头角. 这些方法在构建合理环境的前提下, 可一定程度上摆脱数据集的束缚. 有望在未来通过生成对抗模仿学习、深度强化学习等方法, 构建与力学原理相结合的材料优化设计模式, 充分挖掘人们难以认识到的复合材料规律, 设计出具有多种优异性能的复合材料.
5 复合材料智能制造
在实际工程应用中, 内部的缺陷和损伤会显著降低复合材料的力学性能, 使其无法达到预期的设计目标. 在复合材料的成型及加工过程中, 借助传感器得到复合材料在不同工艺条件下的状态, 并调整相应的工艺参数, 可以有效地减少复合材料的缺陷和损伤. 在复合材料装配、服役的过程中, 利用传感器获取数据进行健康监测, 定期对复合材料健康状态进行检测, 实现复合材料的损伤识别及预警, 准确把握复合材料结构的健康状态, 制定优化维护策略, 可以有效提升复合材料结构件的使用安全性. 相较于复合材料的性能预测与设计, 成型、制造、健康监测及检测中传感器得到的数据规模更大, 维度更广, 更有利于同人工智能方法相结合. 目前, 采用无监督学习可以实现对于不同的缺陷及损伤是否存在的判断, 监督学习则被应用于缺陷及损伤的分类及量化. 将人工智能应用于复合材料的制造及健康方面具有以下优势: (1)减少复合材料成型及加工过程中的缺陷及损伤, 获得设计预期的力学性能; (2)提升复合材料健康监测及检测精度, 实现对微小损伤的捕捉; (3)缩减复合材料无损检测时间, 大幅提升检测规模.
5.1 复合材料成型工艺
在复合材料成型中, 确定恰当的工艺参数对获得高性能复合材料至关重要. 在传统的复合材料成型工艺中, 对工艺参数的制定主要集中在基体方面. 在应用广泛的树脂基复合材料中, 树脂基体的固化制度的制定至关重要, 不合理的固化制度会产生较大的固化变形和残余应力, 导致复合材料无法进行装配或承载能力大幅降低. 采用数值模拟数据训练人工神经网络, 可实现对树脂固化过程中树脂的温度和固化度等信息的快速预测, 防止温度过冲或固化度不足导致零件报废(Rai & Pitchumani 1997, Su et al. 1998). Pagano等(2014)采用混合神经网络模型描述固化动力学, 结合粒子群优化方法设计了纤维缠绕工艺中的固化制度, 提高了固化程度, 缩短了加工时间.Stamopoulos等(2018)制备了在不同热压罐压力下的复合材料单向板, 采用人工神经网络建立了热压罐压力与复合材料孔隙率、力学性能之间的关系. Luo L 等(2020)针对非对称铺层的碳/环氧复合材料的固化过程, 进行了热力耦合的有限元分析, 依据有限元数据构建人工神经网络, 快速预测不同铺层复合材料的固化后变形, 为利用非对称铺层设计实现特定形状的复合材料提供了依据. 但他们的预测结果只能应用于同样材料、形状的复合材料, 普适性更强的人工神经网络仍需高通量、高维度的数据进行训练. 除利用神经网络进行固化过程的预测, Aleksendrić 等(2016)还进一步结合遗传算法对固化制度进行了优化, 有助于实际生产过程中良好固化制度的制定. 神经网络与遗传算法的结合还可以实现对树脂传递模塑(resin transfer molding, RTM)工艺中树脂流动状态的实时预测, 制定合理的树脂注入/流出口布局, 得到稳定、均匀的树脂流动前沿, 减少复合材料孔隙率(Luo et al. 2001), 或对铝基复合材料的温度梯度、冷却速率进行优化设计, 获得更高的力学性能(Mazahery & Shabani 2012, Shabani & Mazahery 2012, 2013).
作为先进的复合材料自动化成型技术, 自动纤维铺放可以对大曲率复杂曲面进行自动化铺放, 成型效率高, 被广泛应用于大型客机及其他航空航天器的制造中. 但由于温度、铺放速度、纤维张力、铺放路径等的影响, 目前在自动纤维铺放中仍会产生一定的缺陷. 将人工智能手段引入自动纤维铺放工艺中, 可以实现对于成型中缺陷的自主检测、判断, 纤维铺放路径的智能规划, 进一步提高成型精度及效率. Sacco等(2020)如图10所示, 将视觉模块采集的图像由全卷积神经网络进行语义分割, 判断如间隙、扭曲、褶皱等缺陷区域, 并采用Marching Squares算法生成修补路径, 驱使机械臂对缺陷处进行修复. 该方法将人工智能与精密机器人系统相结合, 进一步提升了自动纤维铺放工艺的制造精度. Vijayachandran等(2020)构建神经网络预测了不同纤维铺放角度下复合材料屈曲性能, 并结合遗传算法以最大化屈曲性能为目标对纤维铺放路径进行优化. 相较于传统的直纤维铺放, 优化后的可转向纤维铺放使屈曲性能提升了40%以上.Wanigasekara等(2020)针对自动纤维铺放学习样本数量小、数据难以获得的问题, 采用虚拟样本生成的方法扩充了数据集, 并构建人工神经网络验证了虚拟样本的有效性.
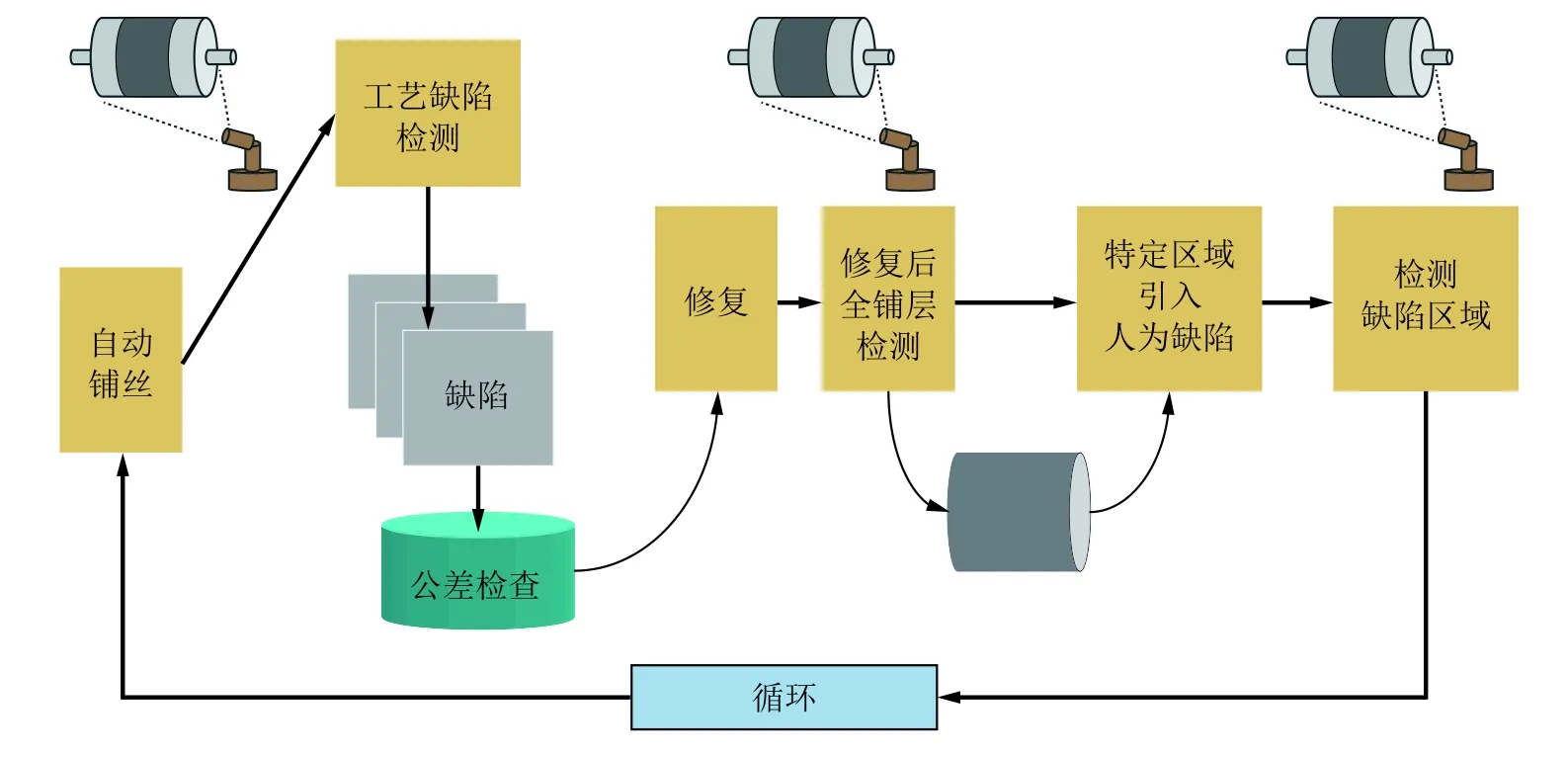
图10
5.2 复合材料加工过程
经过成型工艺制成的复合材料结构件上, 仍有许多装配连接、附件安装所需要的定位面、孔、开口等, 需要进行切削、钻削、铣削等精密加工. 不同于传统材料, 复合材料加工往往较为困难, 易出现分层、撕裂、烧蚀等损伤, 刀具磨损也较为严重, 加工质量难以保证. 利用人工智能技术, 可以对复合材料机械加工过程中的热学、力学问题进行建模, 探究加工参数对复合材料加工质量的影响. 例如, António等(2007)在人工神经网络的学习过程中使用遗传算法调整超参数,实现了对聚醚醚酮基复合材料正交切削加工中力学行为的建模. Hanafi等(2012)采用模糊逻辑方法, 由复合材料切削过程中切削速度、进给速度、切削深度预测了切削力和比切削压力. Tsao(2007)利用径向基函数网络, 建立了复合材料钻削加工中进给速率、主轴转速和直径比与钻削推力之间的关系. Latha和Senthilkumar (2009, 2010)根据实验数据构建了基于规则的钻削推力模糊逻辑模型, 通过钻头直径、进给速度以及主轴转速预测钻削的推力和表面粗糙度, 并表明进给速度以及钻头直径是影响钻削推力和表面粗糙度的主要因素. Bobbili等(2020)基于自组织映射网络方法, 建立了玻璃纤维编织复合材料钻削过程中钻顶角、进给速度及主轴转速与钻孔推力、孔表面粗糙度、毛刺高度之间的关系. Babu等(2020)运用模糊推理系统对碳玻混杂纤维增强复合材料的钻孔行为进行了建模, 表征了主轴转速、钻头直径、进给速度等工艺参数与推力、扭矩、分层因子及表面粗糙度之间的关系. 部分研究者还采用人工智能方法对一些非机械加工方式进行了研究. Antil等(2020)利用人工神经网络预测了碳化硅/环氧复合材料在不同电化学放电加工参数下的钻孔的材料去除率以及锥度. Solati等(2019)构建人工神经网络预测了不同工艺参数下激光钻孔的热影响区域以及承载强度, 表明随热影响区域面积的增大, 被加工件的承载强度显著降低. 适当控制激光钻孔的参数以减小热影响区域, 可以获得比机械钻孔效果更好的加工件.
此外, 还可以通过加工过程中传感器获得的信号, 由人工智能方法实时监测刀具和被加工件的状态, 对加工全过程进行捕捉、分析, 实现动态的感知、判断、优化. 如图11所示, Wang,Dixit 等 (2020)在亚麻纤维增强复合材料的正交切削过程中, 引入多传感器的数据采集系统对复合材料加工过程中声发射信号和振动信号进行提取. 利用随机森林算法将特定频段上的信号与加工条件、工件状态相关联, 实现了对于加工状态的监测, 同时为加工条件的优化提供了可能.随后, 他们又基于声发射监测的方式, 与双向门控循环神经网络相结合, 动态地通过声发射信号对加工状态进行了表征(Wang , Chegdani et al. 2020). 通过六种不同的切削速度和三种不同的切削方向对该循环神经网络的性能进行了评估, 表明其准确度约为87%. 该方法有望实现在加工过程中实时调整加工参数, 以达到更为优良的加工效果.
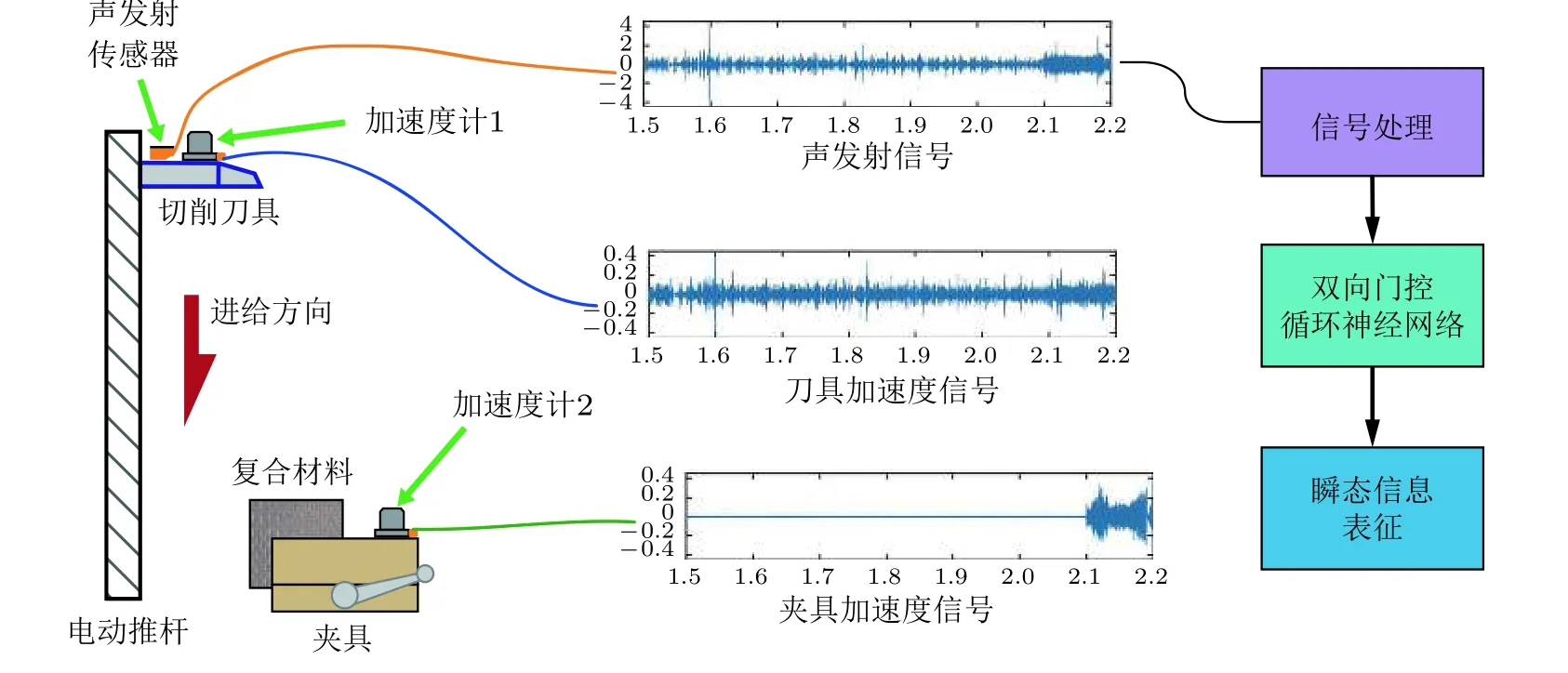
图11
5.3 复合材料无损检测
无损检测是通过合理有效的检测手段, 及时、准确地发现复合材料内部的损伤, 评估复合材料的安全性、可靠性. 复合材料在正常服役条件下通常不会发生突然的破坏, 其失效往往是由于损伤的不断积累, 因此采用无损检测方法对复合材料进行检测可以及时发现问题, 有效规避风险, 提高复合材料使用的安全性. 现有的无损检测方法在获得检测信号后, 通常还需要人工判断是否有损伤或损伤的部位. 采用人工智能技术对检测信号进行处理, 可以实现对损伤自动、高效的判断, 对细微特征信号的捕捉. Graham等(2004)基于高温超导量子干涉仪的检测数据, 采用梯度阈值检索函数进行特征提取后建立人工神经网络成功判断了复合材料冲击损伤的位置. 该方法有效提升了无损检测的效率, 特征提取也使得在数据含有环境噪声下的检测精度有所提高.针对复合材料夹心结构, Just-Agosto等(2008)利用振动的模态响应识别面板、界面及夹心的损坏, 热成像技术对振动分析无法检测的细小穿孔进行补足, 贝叶斯神经网络将二者数据相结合进行建模, 实现了对复合材料夹心结构损伤的类型、位置以及大小的精确检测. De Fenza等(2015)在使用兰姆波的无损检测中, 根据检测信号定义了损伤指数作为结构破坏的决定因素, 并进一步引入了人工神经网络和概率椭圆方法, 实现了对于复合材料损伤的识别. Xu 等(2019)对湿热环境下产生损伤的复合材料单搭接接头的声发射数据, 对主成分进行分析选取关键参数后, 利用改进的K均值聚类方法确定了检测信号与损伤模式间的关系. Liu P 等(2019)在59.5 m长的复合材料风机叶片上布置传感器阵列, 对检测信号进行快速傅里叶变换和时差分析定位损伤源, 并使用K均值聚类方法识别了不同的损伤模式. 该方法充分考虑了超声信号在叶片中的衰减规律, 实现了对在大型复合材料结构件中的损伤进行精确判断和定位. Khatir等(2019)针对复合材料层合板的振动建立了等几何分析方法, 根据结果确定了带有不同损伤的层合板的Cornwell指数, 并建立了与粒子群优化算法相结合的人工神经网络, 对复合材料层合板的损伤进行量化, 大幅缩减了无损检测所需要的时间. Cacciola等(2013)以超声检测为基础, 结合贝叶斯神经网络对复合材料进行无损检测. 不同于其他研究者将检测数据置于计算机上进行离线处理, 他们通过现场可编程门阵列的可重新编程性在实际应用中迅速改变网络的参数, 成功实现了增量学习, 对未来实现无损检测的在线学习具有重要意义.
连续纤维增强复合材料是目前复合材料结构件的主要应用形式. 由于在厚度方向缺少增强,其层间性能相较于面内性能较为薄弱, 因此分层成为一种主要损伤形式. 分层损伤会导致复合材料的强度及刚度显著降低, 造成结构的灾难性破坏, 不利于复合材料服役过程中的稳定性、安全性. 上述无损检测方法也同样适用于复合材料的分层检测, 例如将人工神经网络与声发射技术结合, 可以实现对分层损伤定性、定量的分析(Su & Ye. 2004, 2005; Pan et al. 2006). 除此之外, 根据损伤理论, 复合材料发生分层后其模态及固有频率会发生显著改变, 因此基于模态响应和固有频率的分析被广泛应用于分层损伤的检测. Okafor等(1996)根据分层损伤理论模型及实验得到的数据训练人工神经网络, 通过模态频率预测了分层损伤的大小, 取得了较好的效果. Valoor和Chandrashekhara (2000)在建立模型时考虑了泊松效应和横向剪切, 使人工神经网络预测的损伤大小和位置更贴近实际. 相较于采用实验或理论模型生成训练数据, 有限元方法能以较低的成本获得大量复杂复合材料结构的数据集, 提升该方法对不同问题的适应性. 利用有限元生成数据集训练的人工神经网络, 在单向板和复杂铺层结构层合板上均展现出了良好的预测效果(Chakraborty 2005, Nasiri et al. 2011). Zhang 等(2019)利用有限元结合人工神经网络的方法对复合材料弯曲板的分层损伤进行检测, 其定位精度可达90.57%. 基于分层理论、高阶电势场和有限元方法建立力−电耦合模型, 可以有效模拟图12中压电传感器的响应, 并训练如多层感知机、支持向量机、卷积神经网络等监督学习方法对分层损伤进行分类、预测(Khan & Kim 2018, Khan A et al. 2019). Zheng等(2009, 2011)则将分层检测中采用的多种神经网络与层次遗传算法、最小二乘法、遗传模糊混合学习算法等相结合, 大幅提高了预测系统的鲁棒性, 对未来的工业应用具有重要意义.
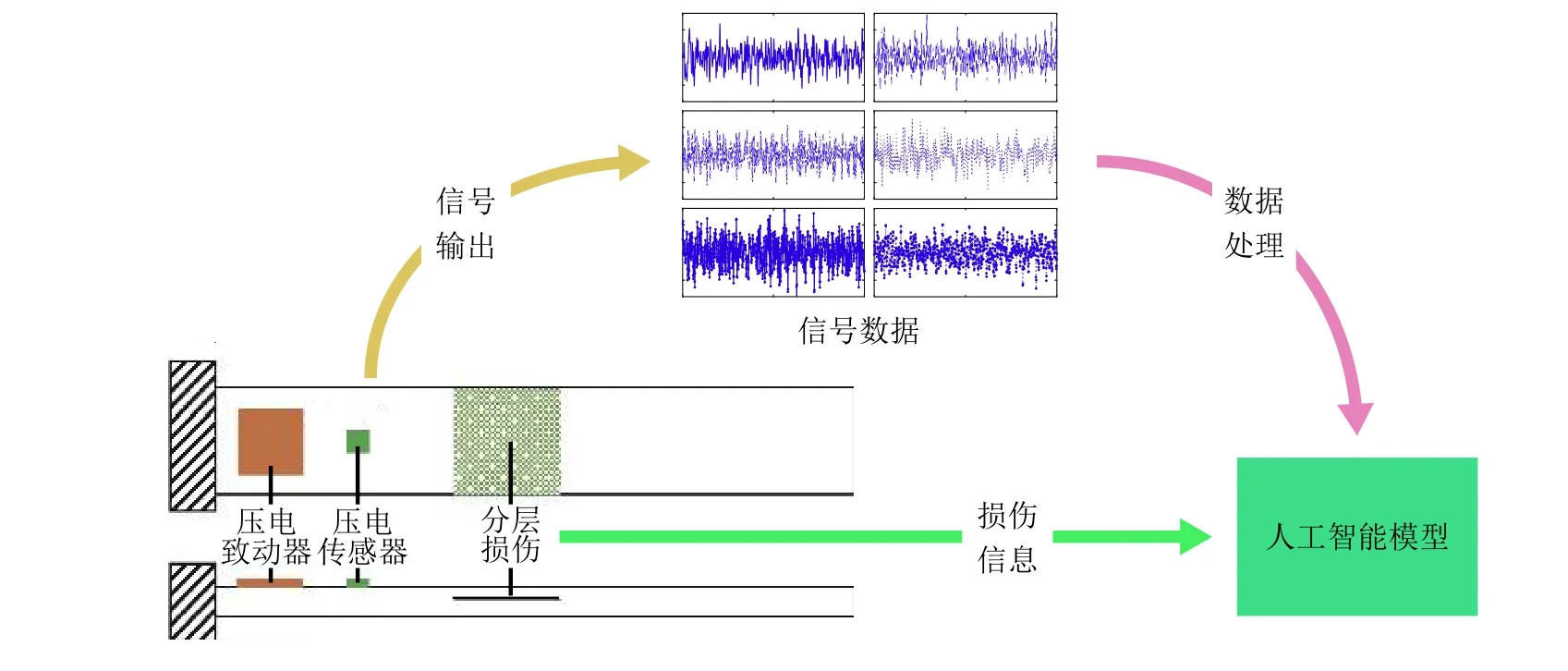
图12
5.4 复合材料健康监测
针对复合材料结构特点及应用环境发展形成的健康监测技术, 可以在复合材料结构使用过程中采集健康状况信息, 提高复合材料结构的安全性. 不同于无损检测技术, 复合材料健康监测以在材料上布置传感器为基础, 实现了对于复合材料状态的实时监测, 减少不可逆损伤的发生,大幅降低了复合材料结构件的维护成本, 提高了复合材料的使用安全性(Worden & Staszewski 2000). 利用人工智能技术对传感器采集的信号进行自主分析, 可以实现由声、光、电阻等物理信息到复合材料受载、损伤状态信息的智能转换, 而无需人力进行大量判断. Yuan等(2005)基于受损层合板的兰姆波数据, 训练了Kohonen神经网络, 成功实现了对不同损伤模式的实时判别. Song等(2007)根据碳纤维增强复合材料电阻值随施加载荷变化的特性, 采用人工神经网络建立了复合材料电阻值和应变间的关系, 实现了对复合材料简单受载状况的实时监测. Fu T 等(2015)使用菱形光纤声发射传感器阵列检测复合材料受冲击时的应力波, 实现了最大定位误差仅为6.3 mm的高精度监测. Sai等(2019)应用光纤布拉格光栅传感器阵列和窄带激光解调技术,监测复合材料受冲击后的声信号, 建立了基于极限学习机的冲击定位模型, 在500 mm×500 mm正方形板件的冲击定位实验中, 平均定位误差为14.7 mm. 同样使用光纤布拉格光栅作为传感器,Califano等(2020)基于复合材料层合板中的损伤会改变应变分布这一现象, 由人工神经网络实现了“光纤信号−应变−损伤”转换模式. Si和Li(2020)利用声发射和超声方法分别建立了两种损伤指数, 仅利用线性回归就实现了对损伤程度的实时预测. 由于线性回归计算快捷, 实现简单, 有望在未来应用于复合材料结构可靠性的在线评估.
除了将传感器布置到复合材料表面外, 还可在复合材料的内部埋入传感器, 形成如图13所示的“智能复合材料”. 一些智能复合材料还可根据应用场景布置处理器、致动器和修复元件, 结合力学模型以达到自感知、自驱动、自学习、自修复的目标. 以人工智能方法替代传统模型进行判断, 进行智能化的特征提取, 可以具有更高的效率、更好的鲁棒性, 也有利于处理器的微型化, 减少侵入式布置对复合材料造成的损伤. 针对复合材料振动抑制这一问题, 传统的智能复合材料一般通过内置的压电传感器感知材料当前振动状况, 而后结合动力学方程, 驱动压电致动器削弱复合材料的振动直至稳定(Saravanos et al. 1997, Narayanan & Balamurugan 2003). 而通过仿真数据训练如人工神经网络、对角递归神经网络等人工智能模型, 并在智能复合材料中代替传统的动力学方程, 使其对复杂载荷环境的适应性有所提高, 具有更好的鲁棒性(Valoor et al. 2000,Srivastava et al. 2016). 在智能复合材料的损伤判断中, 人工智能模型也有效实现了对损伤位置、状态的准确判断, 甚至对微裂纹损伤的精确捕捉(Larrosa et al. 2014, Geng et al. 2018). Sung等(2016)除利用人工神经网络对冲击损伤进行精确定位外, 还进一步监测了冲击发生的时间和破坏程度, 实现对冲击损伤的溯源. Khan 和Kim (2020)基于复合材料中压电材料的低频响应, 在数据处理时采用主成分分析法剔除了冗余的数据特征, 解决了智能复合材料损伤分类中的过拟合问题. Alvarez-Montoya等(2020)在无人机复合材料机翼前梁中布置了20个光纤布拉格光栅进行应变感知, 采用自组织图和主成分分析方法实现基于应变场的损伤模式识别. 该智能复合材料机翼在实际飞行实验中对于人为引入损伤的检测精度可达98.1%, 为未来实现飞行器复合材料结构的自主损伤监测提供了良好的范例.
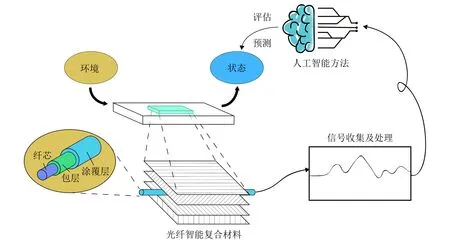
图13
5.5 小结
复合材料成型过程、加工过程以及健康状态的检测、监测是人工智能应用相对成熟的领域.结合人工智能可以提升对于传感器信号数据处理的效率及精度, 并捕捉信号与复合材料状态之间不易发觉的潜在关系. 复合材料在服役过程中通常面临复杂的工作环境, 具有应力场、温度场、湿度场、电场等多场相互耦合的特点. 因此, 目前面临的主要挑战是如何准确地从庞杂的传感器信号中清理噪声信号, 抽取、分离关键特征, 明确各个因素对复合材料状态的影响及时变特性,建立响应数据到材料状态甚至结构性能的关系模式, 实现时间、空间上的连续感知. 除了已被广泛采用的成分分析手段外, 目前蓬勃发展的深度学习在特征抽取上有着显著的优势, 降低了对于传感器信号关键特征的提取难度, 有望在未来实现对具有复杂构型复合材料在多样服役环境下健康状态的精确判断.
6 总结与展望
工程应用领域对具有高力学性能的轻量化材料的需求日益迫切, 如何设计并制造出具有卓越力学性能的复合材料结构, 以进一步发挥复合材料本身轻质高强的优势, 已逐渐成为复合材料研究的核心领域之一. 目前复合材料的设计主要依赖于设计者在生产设计领域积累的经验知识,但这种经验设计的方法往往需要耗费大量的人力物力, 设计周期长, 且无法保证能够达到全局最优解. 近些年来, 与数值模拟相结合的拓扑优化被成功应用于结构设计领域(Sigmund & Maute 2013). 但由于复合材料本身的特性, 其拓扑优化计算量巨大, 设计约束难以明确, 且难以保证优化后的工艺性. 如何摆脱传统先验式、积木式的设计方法, 实现对复合材料设计空间进行智能探索, 缩短设计周期, 提高设计质量, 将是复合材料未来研究的新需求.
近些年来, 随着人工智能技术的不断发展, 为如生物、医药、地球物理等许多传统研究领域的研究者们提供了新思路、新方法. 在复合材料领域, 人工智能方法也正在蓬勃发展. 基于人工智能方法的材料性能预测, 已逐渐形成以实验结果为基础, 以数值模拟方法生成数据集, 以人工智能方法进行建模预测的成熟范式. 而最近提出的多精度深度神经网络可以由大量低成本、低精度的数据捕捉趋势特征后, 对少量的高成本、高精度数据进行精确拟合, 在复合材料的多尺度、高保真性能预测中有着巨大的应用潜力(Meng & Karniadakis 2020, Motamed 2020). 人工智能赋能下的“性能预测−材料设计”这一迭代优化设计模式也已有雏形, 强化学习在材料的精准逆向设计中也有着广阔的前景. 将复合材料设计制造、状态监测与人工智能、大数据、新型制造方法相结合, 势必成为复合材料发展的新趋势.
3D打印技术在复合材料领域的应用, 为复合材料的快速制造提供了可能. 目前, 人工智能技术已初步应用于3D打印产品的设计、实时监测和工艺参数的调整(亓欣波等2019, Jin et al.2019). 但已有的大多数3D打印方法均是沿Z方向逐层积累打印材料的“2.5D打印”, 且打印范围较小, 不能充分发挥复合材料力学性能上的优势(吴陈铭等2019). 以机械臂为基础的多自由度3D打印技术则成为解决上述问题的关键. 在多自由度3D打印中, 曲面层打印下的切片和路径规划、视觉反馈用于精准定位、多机协作打印提升灵活性等问题亟需人工智能的智能优化、机器视觉、多智能体等技术赋能. 因此, 有望在“性能预测−材料设计”这一模式完成设计后, 基于多自由3D打印方法快速制造具有复杂构型的复合材料.
随着大数据时代的来临, 数字孪生技术在复合材料的制造加工、缺陷控制、状态监测等领域也逐渐开始兴起(Eder & Chen 2020, Ghanem et al. 2020, Polini & Corrado 2020, Seon et al.2020). 结合人工智能技术, 数字孪生可以在计算机中快速建立数字模型, 将产品设计、制造中的多种不确定性综合考量, 利用传感器不断引入海量数据驱动数字模型的状态趋近于实体. 数字模型与实体状态互为补充, 实体状态提供数据弥补数字模型的非真实性, 实现完全仿真, 数字模型补充实体状态数据的非完整性, 实现对实体全方位的预测与诊断. 将人工智能与数字孪生技术结合, 有望在未来实现: (1)预先对复合材料进行虚拟的设计、制造、装配及分析, 加速设计方案改进. (2)实时监测复合材料结构件的外部环境和内部状态, 实现智能评估、环境优化. (3)对复合材料结构件的检测与维修, 由现在的“出现问题后诊断”到全寿命的实时诊断, 乃至对结构状态实现预先诊断以实施预防性的保护措施, 增强复合材料结构件的安全性.
目前, 人工智能在复合材料的设计、制造和健康监测等方面仍处于相对初步的阶段, 但已经展现出非凡的潜力. 有理由期待在未来, 以人工智能技术为桥梁, 将力学、材料、机器人、计算机等学科在复合材料领域紧密连接, 为复合材料技术注入新的生机与活力.
致 谢 国家杰出青年科学基金(11625210)、国家重点研发计划(2020YFB0311500)、上海市浦江人才计划(2020PJD072)以及中央高校基本科研业务费专项资金资助项目.
