压电与摩擦电复合型旋转能量采集动力学协同调控机制研究1)
2021-12-21赵林川邹鸿翔刘丰瑞魏克湘张文明
赵林川 邹鸿翔 刘丰瑞 魏克湘 张文明,3)
* (上海交通大学机械系统与振动国家重点实验室,上海 200240)
† (湖南工程学院汽车动力与传动系统湖南省重点实验室,湖南湘潭 411201)
引言
物联网技术的蓬勃发展开启了万物互联的时代,带领人类进入一个智能化的世界,如智能可穿戴设备、智慧家居、智能工业等[1-2].物联网的基础是数以亿万计的广泛分布的智能传感器,可以进行信息和数据的获取、分析、处理和传输[3-5].然而,如何为这些分布范围广、数量大的传感器提供长期有效的电能是物联网技术发展的瓶颈问题之一[6-8].目前大多数传感器采用化学电池供能,虽然电池性能也在不断优化,但是仍旧存在环境污染、需要定期更换维护的问题[9-11].旋转能量是环境中最普遍存在机械能量之一.如果将旋转能量合理转换为电能,为物联网广泛分布的传感器供电,是一种零碳环保、灵活便捷、可持续的供能方式[12].
旋转能量采集技术具有能量来源广泛、设计灵活的特点,按照机电转换机制分类,主要可以分为电磁式、压电式和摩擦纳米发电机.电磁式旋转能量采集器可以依靠叶片、齿轮、轴承等机构直接采集旋转能量,也可以利用惯性结构将其他形式的能量转换为旋转能量再采集和利用[13].Cai 和Liao[14]设计了一个带有偏心质量的可穿戴智能手表,可以将手臂的运动转换为行星齿轮相对于线圈的转动,基于电磁感应发电.Wang 等[15]提出了一种摆锤结构,利用其重力切向分量的周期性变化使系统的固有频率与车轮的旋转速率匹配,提高线圈与磁体的相对摆角,可以为胎压监测传感器供能.Zhang 等[16]设计了一种圆形海尔贝克阵列式的电磁能量采集系统,可以与轴承集成采集旋转机械的能量.装置可以在600~1000 r/min 的转速范围内工作,最大电压为4.59 V.此外,也可以通过巧妙的结构设计利用压电效应直接采集旋转能量.Zhao 等[17]设计了圆周阵列的磁耦合弯张换能器,利用旋转磁体的磁力周期性地激励弯张换能器中的压电片而产生电能,具有高鲁棒性和高可靠性.摩擦纳米发电机是基于摩擦起电和静电感应而发电,具有材料轻便易获取、低频效果好,输出电压高等优点[18-19].在旋转能量采集中,由于两层材料分离,可以分别固定在转子和定子上,有利于其与转子系统集成.Xie 等[20]提出了一种旋转叶片式的摩擦纳米发电机,利用推杆和两个飞轮结构的配合将脚踏能量转化为飞轮的高速旋转基于独立层模式而产生电能,有希望监控司机的驾驶习惯.利用接触分离模式和水平滑动模式的复合,一种旋转风能采集系统被提出,并且器件可以在约15 m/s 的风速下产生250 V 的开路电压[21].为了可以更加灵活的设计和布置,可以将旋转运动转换为悬臂梁的振动基于压电效应而发电[22].Khameneifar 等[23]将带有末端质量的压电梁圆周阵列在转子上,利用末端质量的重力作为激励使压电梁产生形变,并研究了不同压电材料在不同转速下的电学输出性能.将旋转转换为振动进行压电能量采集虽然提高了设计灵活性,但是也带来了新的挑战,比如振动能量采集系统对激励更加敏感,低频激励下性能较差;压电梁在强激励下可靠性较差.
尽管旋转能量采集已经被广泛地研究,对于低转速下的旋转能量采集系统仍旧存在电学输出效果差难以满足实际应用需求的问题[24].Zhai 等[25]采用齿轮组升频的方式,将低速水流激励转化为齿轮的单向高速转动,再通过机电转换产生电能,有希望解决低频波浪能量采集的难题.Kim 等[26]设计了海尔贝克阵列与齿轮组配合的方式,优化磁场强度并提升频率,可以提高低频旋转能量采集的功率.然而齿轮组和磁体阵列的结构复杂,不利于其与系统集成和小型化.Mei 等[27]利用刚度软化效应设计了一个旋转能量采集器,能够采集转速75~ 120 rpm 范围内的能量,最大电压为4 V.Zou 等[28]提出了一种用于旋转运动的磁耦合二自由度振动能量采集器,利用刚度软化效应提升低速能量采集的功率.但是过低的刚度和过大的振动位移会使悬臂梁极易损坏,工作频域窄,可靠性差[29].
虽然这些方法在一定程度提升了旋转能量采集系统的性能,但是尚未兼顾能量采集系统的低频宽频激励的适应性、输出功率和可靠性.这些方法是被割裂使用的,它们之间的相互影响与协同效应考虑很少或尚未涉及.本文提出了动力学协同调控机制用于提高旋转能量采集系统的性能,可以使器件在低转速激励下(0~ 250 r/min)有效工作,增加输出电能和提高器件可靠性.旋转刚度软化、非线性磁力、几何边界的协同调控既可以增加系统在低速下的振动位移以及压电材料的形变,也能在系统振动位移过大时调控系统的最大位移,使其振动可控并提高可靠性.此外,几何边界可以方便地集成摩擦纳米发电机,实现压电与摩擦两种机电转换机制分别在振动和碰撞过程协同发电,有效利用空间和增加输出电能.基于哈密顿原理建立了系统的机电耦合动力学模型.加工了原理样机并在不同工况下进行了实验研究,以期为能量采集系统动力学和电学性能改进提供新的途径.
1 动力学协同调控原理与结构设计
1.1 动力学协同调控原理
本文提出的动力学协同调控机制的工作原理如图1 所示.首先将悬臂梁倒置安装在旋转盘上,即将悬臂梁的夹持端远离旋转中心,自由端靠近旋转中心,这种方式使得离心力与悬臂梁变形方向相同,可以使得悬臂梁在旋转过程中产生刚度软化效应,有利于悬臂梁在低速下产生较大形变.然而,随着转速升高,刚度软化效应更加显著,悬臂梁的振动位移可能过大甚至可能造成压电梁损坏,如图1(a)所示.因此,本设计提出了刚度软化、非线性磁力、几何边界协同动力学调控机制,如图1(b)所示:引入了非线性磁力双稳态机制,进一步降低能量采集系统工作频率;在悬臂梁两侧对称设置几何边界限制悬臂梁的过大位移不仅可以使系统振动更加可控,还可以避免压电梁损坏提高系统可靠性.此外,几何边界可以方便地集成摩擦纳米发电机,实现压电与摩擦两种机电转换机制分别在振动和碰撞过程协同发电,有效利用空间和增加输出电能.同时,非线性磁力也可以提高悬臂梁与边界之间的碰撞力,有利于摩擦纳米发电机的电荷转移.压电单元基于压电效应而产生电能;摩擦纳米发电机在功能材料接触时发生电荷转移从而在两侧材料表面产生等量正负电荷,然后由于周期性接触分离导致电势差变化,基于静电感应在两电极之间的外电路内产生电荷流动而发电.

图1 低转速下动力学协同调控机制示意图Fig.1 Schematic diagram of dynamic coordinated modulation mechanism in low rotational speed range
1.2 结构设计
图2 为具有动力学协同调控机制的旋转能量采集器(REH-DCMM)的设计示意图.REH-DCMM 系统主要由框架、悬臂梁、几何边界、一对相互排斥的永磁体、压电单元PEH 和摩擦纳米发电机TENG构成.框架通过3D 打印技术将几何边界、悬臂梁夹持端和器件保护罩一体化成型.悬臂梁夹持端通过螺栓与框架固定,并在靠近夹持端粘贴压电层,形成压电单元.在悬臂梁中部区域,由内至外分别粘贴铜电极和FEP 薄膜.几何边界相应地对称布置在悬臂梁中部区域的两侧,并在两个边界内侧分别粘贴铜电极,形成两个对称的摩擦纳米发电机.在悬臂梁的自由端固定一块末端永磁体,并在前端框架中部嵌入一块静态永磁体,两块磁体同名磁极相对,产生排斥力.REH-DCMM 系统方便加工和装配,也很容易地集成单元进行阵列排布.将REH-DCMM 系统倒置安装在旋转机械上,末端永磁体的重力在旋转作用下,作为周期性外激励,将旋转运动转化为悬臂梁周期性振动,可以有效采集旋转设备在低转速范围内的旋转能量.

图2 具有动力学协同调控机制的旋转能量采集器(REH-DCMM)的设计示意图Fig.2 Design of the rotational energy harvester with dynamic coordinated modulation mechanism (REH-DCMM)
2 动力学建模
基于哈密顿原理对REH-DCMM 系统进行动力学建模,REH-DCMM 系统的动力学模型示意图如图3 所示.OXYZ为惯性坐标系,ORXRYRZR为旋转坐标系,系统的旋转角度为 β,角速度为 ω.在刚度软化效应下,系统的动能可以表示为


图3 REH-DCMM 系统的动力学模型示意图Fig.3 Schematic diagram of dynamic model of REH-DCMM system
式中,R为悬臂梁的夹持端到旋转中心的距离,ψ(x,t)为悬臂梁的挠度,表示ψ对t求导数,θ 为悬臂梁末端永磁体的偏转角,,tm为永磁体的厚度,m为末端永磁体的质量,s1为压电材料的长度,s2为悬臂梁的长度,ρs,ρp和 ρT分别表示悬臂梁,压电材料和摩擦材料的密度;As,Ap和AT分别表示悬臂梁,压电材料和摩擦材料的横截面积;Is,Ip和IT分别表示悬臂梁,压电材料和摩擦材料的转动惯量.
系统在刚度软化效应下的弹性势能可以表示为
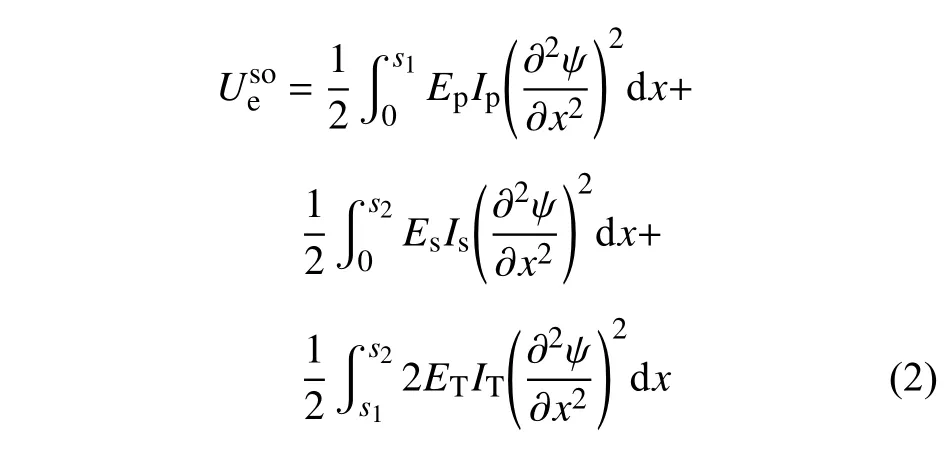
式中,Es,Ep和ET分别表示悬臂梁,压电材料和摩擦材料的弹性模量.
REH-DCMM 系统在刚度软化效应下的离心势能可以表示为

REH-DCMM 系统在刚度软化效应下的重力势能可以表示为
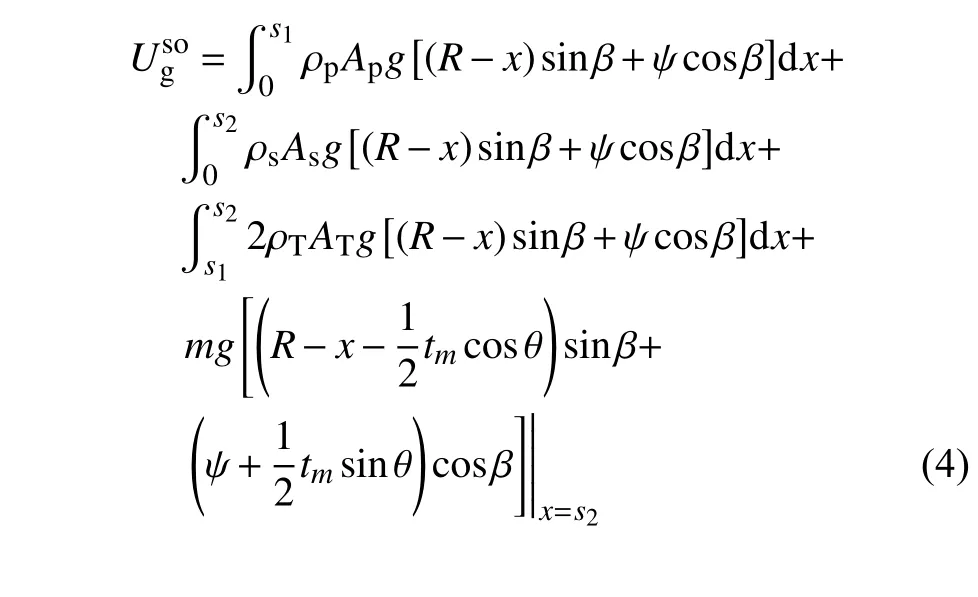
式中,g为重力加速度且g=9.8 m/s2.
压电材料在d31模式的弯曲焓可定义为

式中,Cp为电容,Cp=ε33bs1hp,e31为机电耦合系数,ε33为压电材料介电常数,Vp为压电材料产生的电压.
此外,根据文献[30],永磁体可以定义为点磁极,悬臂梁末端永磁体的磁矩矢量可以表示为
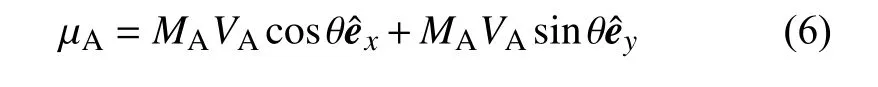
式中,MA为末端磁体磁化矢量,MA=Br/μ0,Br为剩余磁通密度,μ0为真空磁导率,VA为末端磁体的体积.同理,框架中固定的静态永磁体的磁矩矢量可以表示为

式中,MB为静态永磁体的磁化矢量,MB=Br/μ0,VB为静态永磁体的体积.从点磁极μB到点磁极 μA距离可以表示为

式中,d为悬臂梁末端磁体与静态永磁体在XR方向的距离,h为悬臂梁末端磁体与静态永磁体在YR方向的距离,分别表示为
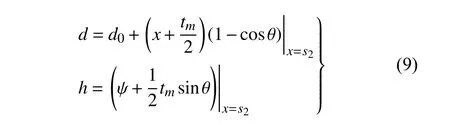
式中,d0表示当ψ|x=s2=0时悬臂梁末端磁体与静态永磁体间在XR方向的距离.末端磁体在静态磁体位置产生的磁场可定义为
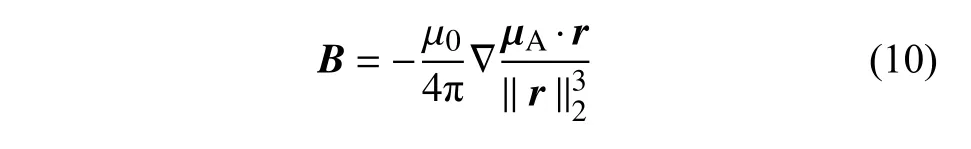
式中,∇ 为向量梯度算子,‖ ‖2为欧几里德范数.因此,REH-DCMM 系统的磁势能可以表示为

如果不考虑机械能量损失,非保守力的虚功可以表示为

式中,c为机械阻尼系数,Q为通过压电单元负载电阻的电荷量,=Vp/Rp,Rp为压电单元负载电阻.由于在悬臂梁振动时,第一阶模态占主导地位,基于伽辽金法悬臂梁的横向位移可表示为
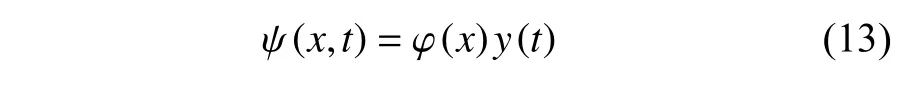
式中,φ(x) 为悬臂梁的第一阶模态振型,φ(x)=1-,y(t) 为广义位移.
根据哈密顿原理,考虑刚度软化效应的REHDCMM 系统的拉格朗日方程可以表示为
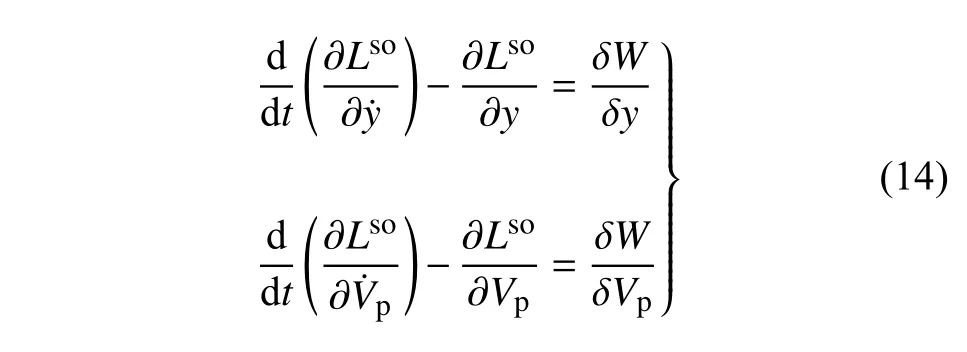
式中,Lso=Tso-Uso-Um-.因此,REH-DCMM系统的机电耦合动力学方程为

式中,M,C,和K分别为系统的等效质量,等效阻尼和等效刚度; ξ 为机电耦合系数,Fp为非线性几何边界与悬臂梁之间的等效碰撞力,当y<-ym时,Fp=+kp(y+ym),当y>ym时,Fp=+kp(y-ym),当 -ym≤y≤ym时,Fp=0,ym为非线性边界与中心点之间在YR方向的距离;RT1和RT2分别为两个摩擦纳米发电机的负载电阻,QT1和QT2分别为两个摩擦纳米发电机电极间转移的电荷,ε0为真空介电常数,hf和εrf分别为FEP 薄膜的厚度和相对介电常数,S为非线性几何边界与悬臂梁的接触面积,yT1(t)和yT2(t) 分别为悬臂梁到两侧非线性几何边界在YR方向的等效距离,其中yT1(t)=ym-y,yT2(t)=ym+y.
最后,将机电耦合方程(15) 带入Matlab/Simulink 软件使用变步长和ode45 运算器进行数值仿真,相应的初始参数如表1 所示.

表1 REH-DCMM 系统的几何和材料参数Table 1 Geometric and material properties of the REH-DCMM system
3 实验验证
3.1 实验系统
为了分析本文提出的动力学协同调控机制在低转速激励下的动力学特性和电学性能以及验证机电耦合动力学模型,加工了REH-DCMM 的原理样机进行了一系列实验测试,如图4 所示.表1 列举了REH-DCMM 的材料和几何参数.框架通过3D 打印而成,材料为PLA 聚乳酸,悬臂梁的材料为65Mn(ASTM:1566),压电材料为MFC (M2814-P2,XINMINGTIAN).原理样机安装在转盘上,转盘与伺服电机(130AEA38025-SH3,SHIDAICHAOQUN)连接,由伺服控制器(DM-38EA,SHIDAICHAOQUN)控制伺服电机,使样机转速灵活可控.导电滑环(SNG000-20S-Y0033,SENRING)安装在旋转盘的中心,解决旋转过程中的接线绕线问题.原理样机的实验数据由动态数据采集分析系统(DH5902,DONGHUA)记录并处理.
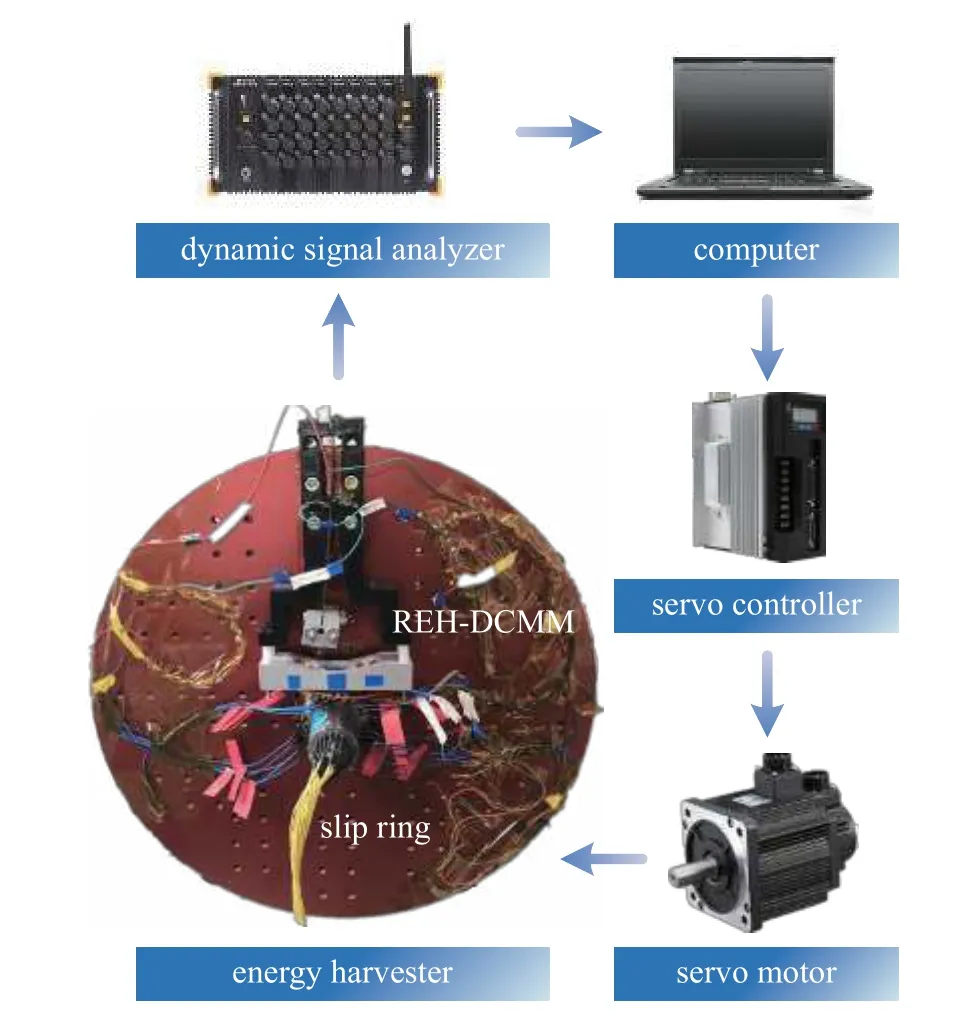
图4 实验装置图Fig.4 Experimental setup
3.2 结果分析及讨论
在不同转速激励下PEH 单元和TENG 单元的实验和仿真电压波形如图5 所示,其中TENG1 和TENG2 分别表示两侧对称的摩擦纳米发电机.当转速为150 r/min 时,REH-DCMM 系统处于混沌振动状态,输出电压波形相对不稳定,但是系统在刚度软化、非线性磁力、几何边界的共同作用下仍旧能够保证有效的电压输出,实验与仿真的电压在趋势上保持一致.当转速增加到250 r/min 时,几何边界限制了梁的振动位移,悬臂梁能够在两侧边界内产生规则的振动.因此,PEH 单元和TENG 单元的电压波形稳定、规律,两侧TENG 单元的电压对称性更好,实验与仿真数据吻合良好.实验和仿真结果的对比说明了本文建立的理论模型能够准确地描述REHDCMM 系统的动态特性和电学响应,可以为设计提供指导.
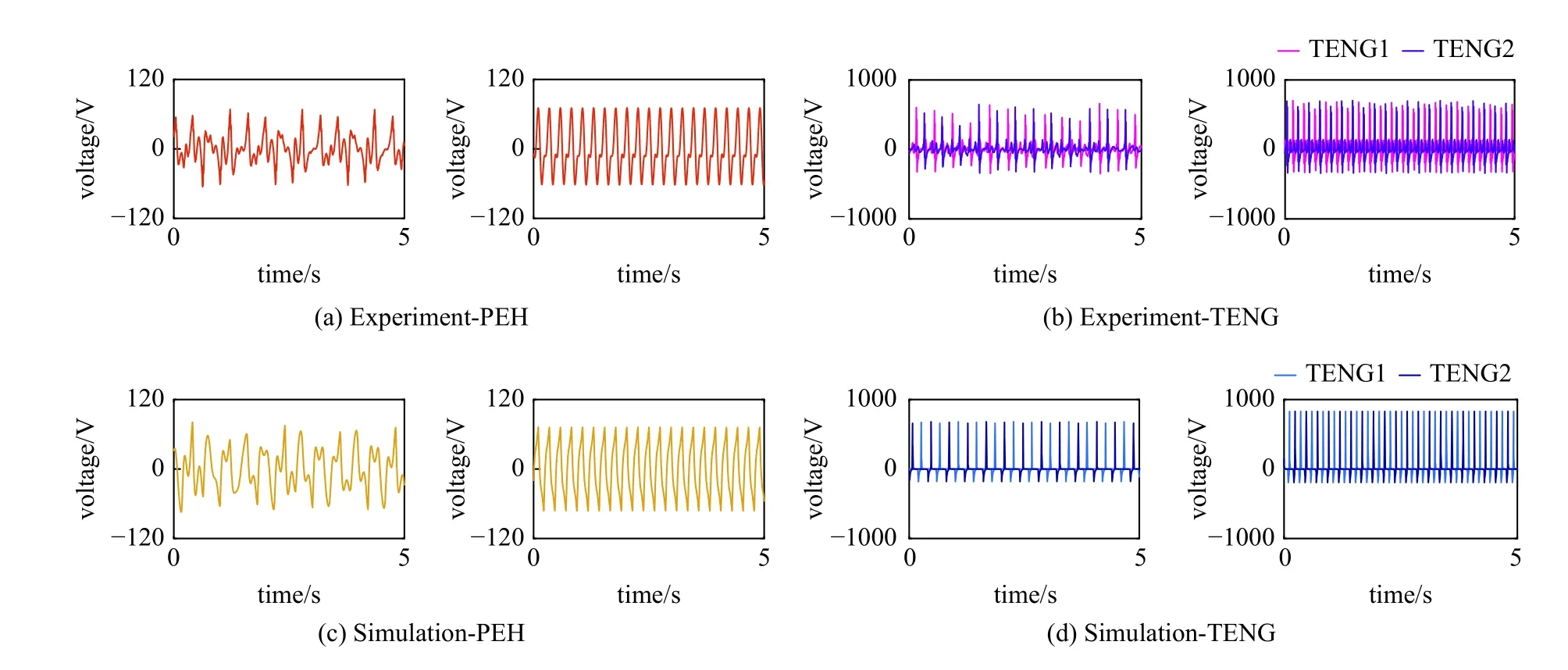
图5 在不同转速激励下PEH 单元和TENG 单元的实验和仿真电压波形图.(a) PEH 单元和(b)TENG 单元在转速为150 r/min 和200 r/min 时的实验输出电压,(c) PEH 单元和(d)TENG 单元在转速为150 r/min 和200 r/min 时的仿真输出电压Fig.5 Comparison of the output voltage of the PEH and the TENG unit from experiments and simulations at different rotational speeds.The experimental voltage from (a) PEH and (b) TENG at the rotational speed of 150 r/min and 200 r/min,the simulation voltage from (c) PEH and(d) TENG at the rotational speed of 150 r/min and 200 r/min
图6 对比了激励转速为0~250 r/min 范围内,REH-DCMM 系统在不同初始磁极中心距(d0=20,22,24 mm)时的峰峰值电压和平均功率.如图6(a)和图6(b)所示,PEH 单元的峰峰值电压和平均功率随着转速的增加而增加,受到磁力的影响不大,在不同磁力下均能产生较高的电压和功率.在转速为250 r/min,初始磁极中心距为20 mm 时,PEH 单元的峰峰值电压为132 V,平均功率为935 μW.这是因为压电单元位于悬臂梁的夹持端,压电效应的效果主要取决于梁根部的形变量,形变越大,电学输出越高.并且由于几何边界的调控,限制了梁的最大位移,磁力对根部形变影响较小.对于TENG 单元,如图6(c)和图6(d)所示,峰峰值电压和平均功率随着转速的增加而增加,并且在同一转速下,磁力越大,电学输出性能越好.在转速为250 r/min,初始磁极中心距为20 mm 时,TENG 单元的峰峰值电压为1128 V,总平均功率为491 μW.这是因为随着转速的增加,悬臂梁与边界之间的碰撞力增加,并且磁力增加也会提高碰撞力,有利于TENG 单元的电荷转移和增加有效接触面积,从而提升TENG 单元的电学输出性能.
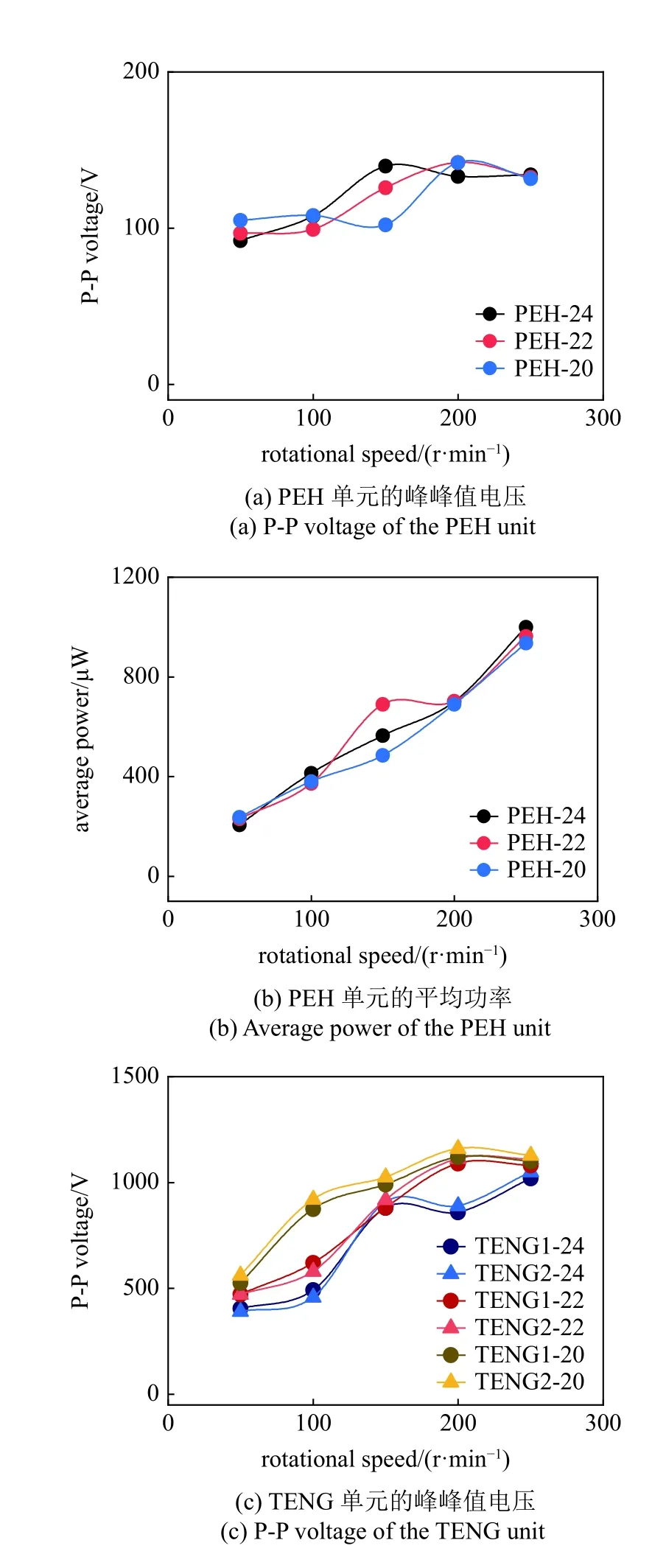
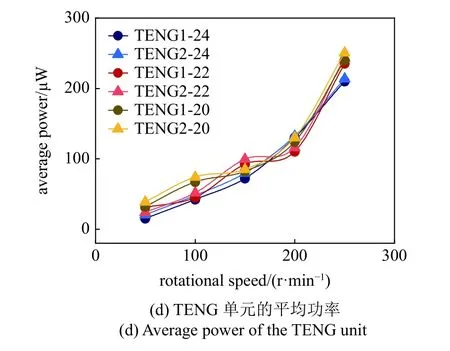
图6 激励转速为0~250 r/min 范围内,REH-DCMM 系统在不同初始磁极中心距(d0=20,22,24 mm)时的P-P 电压和平均功率Fig.6 Comparison of P-P voltage and average power of the REHDCMM with different center distances of the magnetic poles (d0=20,22,24 mm) at the rotational speed from 0 to 250 r/min
图7 对比了激励转速为0~250 r/min 范围内,REH-DCMM 系统在不同悬臂梁厚度(b=0.2,0.3,0.35 mm)时的峰峰值电压和平均功率.如图7(a)和图7(b)所示,当悬臂梁厚度为0.3 mm 和0.35 mm时,PEH 单元的峰峰值电压和平均功率随着转速的升高而增大,并且悬臂梁的厚度越大,PEH 单元的电学输出效果越好.在转速为250 r/min,悬臂梁厚度为0.35 mm 时,PEH 单元的峰峰值电压为140 V,平均功率为1030 μW.因为在相同振动幅值时,梁的厚度越大,应变越大,引起压电层形变越大,则因为压电效应产生的电压越高.类似地,当悬臂梁厚度为0.3 mm和0.35 mm 时,TENG 单元的峰峰值电压和平均功率随着转速的升高而增大,且梁厚度越小,TENG 单元的电学响应越好.在转速为250 r/min,悬臂梁厚度为0.3 mm 时,TENG 单元的峰峰值电压为1076 V,总平均功率为448 μW.主要原因是薄的梁刚度较小,梁的振动位移更大且与边界材料的接触更加紧密而充分,提升TENG 的发电效果.当悬臂梁厚度为0.2 mm 时,在0~150 r/min 范围内PEH 单元和TENG单元的峰峰值电压和平均功率随着转速的增加而变大,当转速继续增加时,由于刚度软化导致梁刚度过低,悬臂梁振动效果变差且与边界难以产生有效接触分离,因此PEH 单元和TENG 单元的电学响应出现下降趋势.
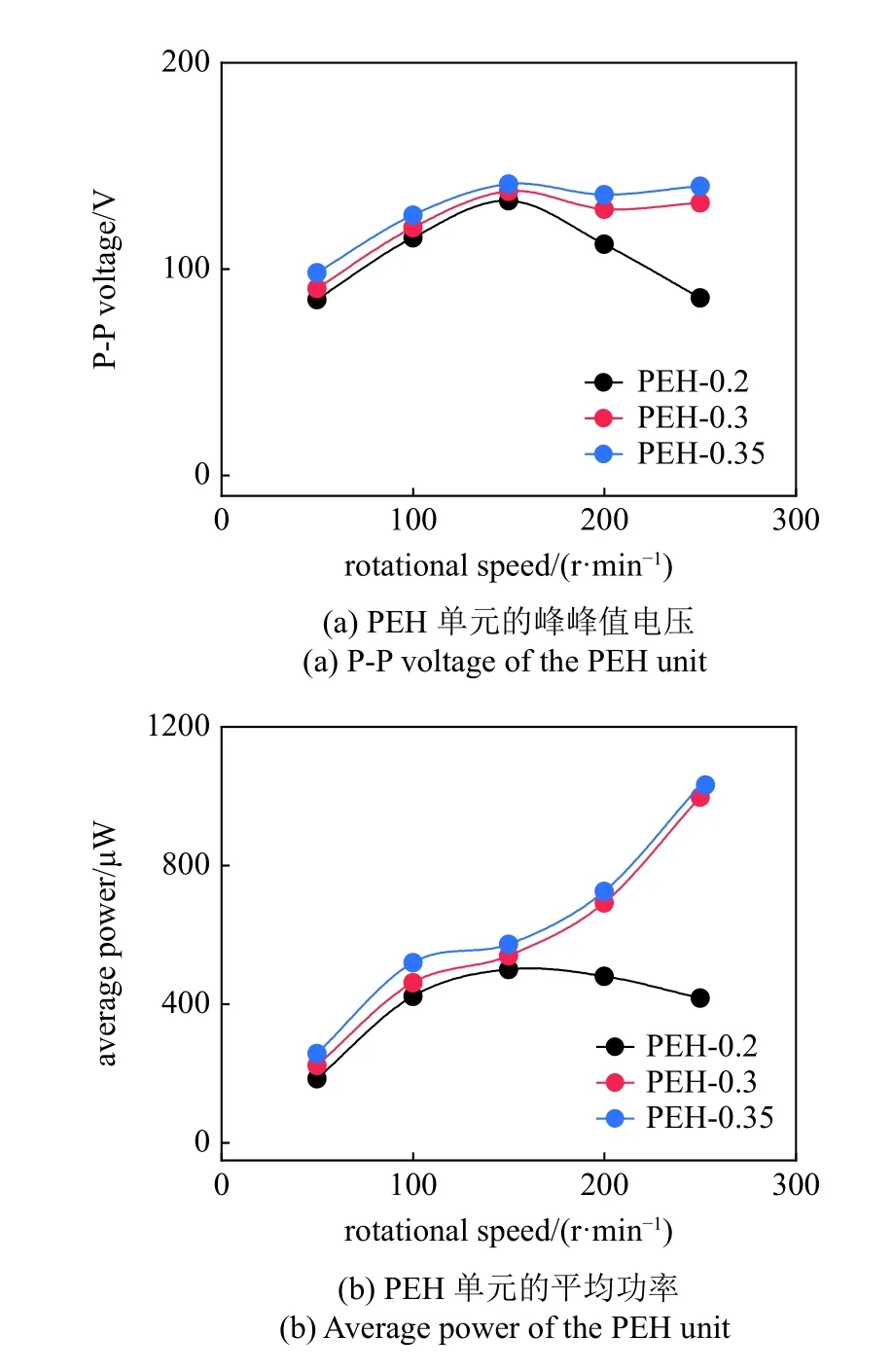
图7 激励转速为0~250 r/min 范围内,REH-DCMM 系统在不同悬臂梁厚度(b=0.2,0.3,0.35 mm)时的P-P 电压和平均功率Fig.7 Comparison of P-P voltage and average power of the REHDCMM with different thicknesses of the cantilever beam (b=0.2,0.3,0.35 mm) at the rotational speed from 0 to 250 r/min
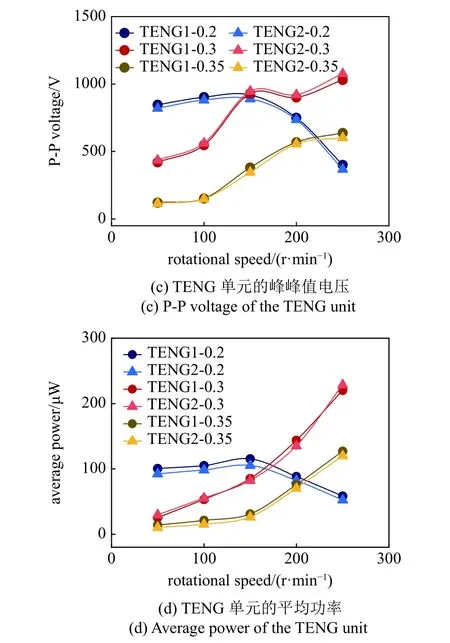
图7 激励转速为0~250 r/min 范围内,REH-DCMM 系统在不同悬臂梁厚度(b=0.2,0.3,0.35 mm)时的P-P 电压和平均功率(续)Fig.7 Comparison of P-P voltage and average power of the REHDCMM with different thicknesses of the cantilever beam (b=0.2,0.3,0.35 mm) at the rotational speed from 0 to 250 r/min (continued)
图8 对比了在磁间距20 mm,梁厚度0.3 mm 的相同参数下,激励转速为0~250 r/min 范围内,REHDCMM 系统在刚度软化和硬化效应下的输出电压.如图8(a)所示,PEH 单元在刚度软化效应下的输出电压高于PEH 单元在刚度硬化效应下输出电压.这是因为,在低转速下,刚度软化可以使梁的刚度降低,提高悬臂梁夹持端的形变,更加有利于压电材料的形变.TENG1 和TENG2 单元分别为两侧对称的摩擦纳米发电机,它们的输出电压在0~250 r/min 范围内受到刚度软化和刚度硬化的影响更明显.低速时,刚度软化可以使悬臂梁自由端更加柔软,与几何边界的接触会更加充分,提高了有效接触面积,有利于两层摩擦材料之间的电荷转移,提高TENG 的输出电压.由此可以证明刚度软化、非线性磁力、几何边界协同调控的机制更加适用于低速旋转能量采集.

图8 在刚度软化和刚度硬化效应下,磁间距20 mm,梁厚度0.3 mm 时,PEH 单元和TENG 单元输出电压对比.(a) PEH 单元,(b) TENG1 单元,(c) TENG2 单元Fig.8 Comparison of the output voltage of the PEH and the TENG unit between centrifugal softening and centrifugal stiffening effects with the same condition (d0=20 mm,b=0.3 mm).(a) PEH unit,(b) TENG1 unit,(c) TENG2 unit
4 结论
本文提出了一种动力学协同调控机制用于低转速下旋转能量采集.刚度软化、非线性磁力、几何边界的协同调控可以提高系统在低速下的振动位移,也可以调控系统的最大振动位移,使系统更可控和可靠性更好.几何边界可以方便地集成摩擦纳米发电机,实现压电与摩擦两种机电转换机制分别在振动和碰撞过程协同发电,有效利用空间和增加输出电能.建立了系统的机电耦合方程并进行了实验验证.主要结论如下:
(1)动力学协同调控机制可以使系统在低转速激励下有效采集能量,系统可以在0~250 r/min 范围内有效工作,在转速为250 r/min 时,压电单元和摩擦纳米发电机的最大峰峰值电压分别为132 V 和1128 V,总平均功率为1426 μW.
(2)在合理范围内,其他参数保持不变时,磁力越大,摩擦纳米发电机的输出电压越大,平均功率越大;压电单元由于几何边界的限制,电压和平均功率随磁力没有显著变化.
(3)在合理范围内,其他参数保持不变时,悬臂梁厚度越小,低转速下摩擦纳米发电机的电学输出效果越好;但梁厚度过小,随着转速增加刚度软化效应导致刚度过低,系统电学输出会降低.
本文提出的动力学协同调控机制考虑了多种性能提升技术的相互影响与协同,为能量采集系统动力学和电学性能改进提供新的途径,可以为物联网中的传感器提供零碳环保、灵活便捷、可持续的电能.
