基于多种土体导热系数模型的潜流带温度场模拟
2021-12-20门利利王大博陈建琪
任 杰,门利利, 2,陈 波, 3,王大博,陈建琪,王 帆
(1.西安理工大学 省部共建西北旱区生态水利国家重点实验室,陕西 西安710048; 2.中国电建集团 西北勘测设计研究院有限公司,陕西 西安 710065; 3.四川省水利水电勘测设计研究院有限公司,四川 成都 610072)
引言
潜流带“Hyporheic zone”是指河流河床以及河岸带饱和沉积层,是地表水与地下水相互作用、物质和能量交换、生物群落生长和繁殖的区域[1-3]。类似于氮、磷等污染物直接或间接排放到水体中,会降低水体有效利用且使得水生系统退化[4-6],而潜流带中地表水与地下水的交换过程对污染物的净化、河流生态健康的调控起着关键作用。生态系统的健康程度依赖于完善的生态系统功能,健康的河流生态系统不仅是国家生态安全体系的重要组成部分,也是经济社会可持续发展的重要基础[7-8]。温度通过影响水的密度、动力粘度以及土壤孔隙度,进而对渗流场造成影响[9-10]。使用水温作为天然的示踪剂,研究河床或河岸带的物理性质和变化过程,对河流水生态系统具有重要的意义[11-12]。
土体导热系数是土体热特性的关键指标之一,是影响土体传热过程中温度分布以及能量变化的主要因素,也是研究流-热耦合作用、物质传输、气体扩散等土壤物理过程的基础[13-14]。Kersten等[15]于1949年提出土体导热系数与容重有关的经验模型,是最早用来预测冻土导热系数的方法之一。Johansen等[16]于1975年提出了归一化导热系数的概念,它在预测不同质地的土壤中普遍具有较好的性能,已被广泛应用。Chung和Horton[17]于1987年提出一个较为简单的经验模型,模型只考虑了含水率对导热系数的影响。Lu等[18]于2007年在Johansen研究的基础上将土体大致分为粗质土壤和细质土壤,引进一个与砂粒含量相关的经验常数。Lu和Dong[19]于2015年提出了闭合形式的土体导热系数经验方程,将土壤水分特征曲线与热传导系数相联系,能够较为准确的预测不同类型土壤的热传导系。Ren等[20]于2019年考虑有机质对导热系数的影响,同时考虑土壤粒组成分对形状因子的影响,在已有模型的基础上提出一个新的经验模型,相比于以往模型,该模型适用范围较更广,拟合效果更好,精度更高。
Witherspoon[21]在20世纪70年代首先提出耦合理论,经过数十年的不断改进,耦合理论被广泛应用于各个领域。Molina-Giraldo等[22]通过建立地表水补给地下水的流-热耦合二维模型,指出非饱和带传热对河岸带的温度分布具有明显影响。Ren等[23]基于室内水槽试验,建立饱和-非饱和流-热耦合模型,研究不同入渗水头、不同水温条件下,砂槽温度的变化规律,结果发现,水槽低温区域随渗入水头的增大而增大,且水温对水槽温度场影响较为显著,模型模拟结果与试验一致。吴志伟等[24]基于Lu模型构建浅部地区温度场和饱和-非饱和渗流场的耦合模型,发现温度场总体上增大时,渗流速度减小,且温度场较渗流场的变化幅度偏小,表明了渗流场对温度场的影响程度较大[25]。于友斌[26]通过Comsol软件构建流-热耦合模型,通过求解得到渗流对冻结温度场与渗流场的影响,并将结果与试验进行比较,结果发现数值模拟温度场与实测温度场规律相同。土壤导热系数作为流-热耦合理论的重要驱动因子,是直接决定模型是否成功和准确的关键,虽然不少学者开展了关于流-热耦合理论模型的研究,但对于基于土壤导热系数与流-热耦合理论之间相互作用并应用于河流地表水-地下水相互作用机理方面鲜有报道。
基于此,本文建立基于HYDRUS软件的Chung & Horton模型以及基于COMSOL Multiphysics软件的Lu(2007)模型、Lu(2014)模型和Ren(2019)模型的河床、河岸带饱和-非饱和流-热耦合模型,通过比较野外试验测得的温度场和4种方法建立的模型计算得到的温度场进行对比分析,以此验证构建的潜流层饱和-非饱和流热全耦合模型的精度和效果,并进行了耦合作用下河床、河岸带的温度、水位、垂向流速、环境温度、水温之间的相关性分析,研究影响温度及其渗流的关键要素,为通过流-热耦合模型研究地表水和地下水相互作用提供理论依据。
1 数学模型
1.1 渗流场模型
饱和-非饱和渗流场采用Richards方程表示[24]:
(1)
式中:ρw为水的密度;Cm为土体容水度;g为重力加速度;Se为土壤的相对饱和度;Ss为弹性贮水率;P为压强; ▽为拉普拉斯算子;θ为土壤含水量;ks为介质饱和渗透系数;kr(θ)为非饱和带相对渗透率(0≤kr(θ)≤1),是含水率θ的函数;μ(T)为水的动力粘滞系数,为温度T的函数[27];z为计算点位置高程;Qs为水流源汇项。
采用van Genuchten模型(简称VG模型)来描述土壤水分特征曲线[28]:
θ=θr+Se(θs-θr).
(2)
式中:Se为土壤相对饱和度;θr为残余含水率;θs为饱和含水率。其中Se为:
(3)
式中:hp为压力水头,hp=pw/ρw,在非饱和带等于负压水头Hc;α和nv为VG模型参数,其中,α为水分特征曲线进气值的倒数,nv为水分特征曲线斜率的指示参数,也是反映土壤孔隙分布的参数;通过拟合土壤水分特征曲线得到,m= 1-1/nv。
土壤容水度Cm和相对渗透率kr分别采用下述经验公式表示:
(4)
(5)
1.2 温度场模型
温度场采用热对流传热方程描述[25]:
(6)
式中:λeq,ρeq,Ceq分别为整个含水层系统的等效导热系数,等效密度以及等效比热容,T为地下水温度,Cw、ρw分别为流体的密度和比热容,u为渗流速度,QG为热量源汇项。
饱和-非饱和土体等效密度以及比热容遵循体积平均定律,其表达式为:
ρeq=(1-n)ρs+θρw+(n-θ)ρg.
(7)
Ceq=(1-n)Cs+θCw+(n-θ)Cg.
(8)
式中:n为多孔介质的孔隙度,当土体处于饱和状态时,即θ=n;ρs、ρw、ρg分别为土、水和空气的密度,Cs、Cw、Cg分别为土、水和空气的比热容。
1.3 土体导热系数模型
1.3.1 Chung & Horton(1987)模型
Chung和 Horton在1987年提出一个较为简单的经验模型,模型只考虑了含水率对导热系数的影响,因此在土壤其他物理参数发生变化的情况下,模拟误差就会较大,模型公式如下[17]:
λ=b1+b2·θ+b3·θ0.5.
(9)
式中:b1,b2,b3为经验常数,其值与土壤的类型有关。
1.3.2 Lu(2007)模型
Lu和Ren在Johansen研究的基础上,采用Johansen的归一化模型,提出一个比较适合低含水率条件下土壤导热系数的计算模型,但因其将石英含量等量为砂的含量,因此不适合用来计算砂土含量较高的土壤导热系数,计算值较实测值偏低[20],模型公式如下[18]:
λ=(λsat-λdry)·Ke+λdry.
(10)
(11)
式中:λdry和λsat分别为干土和饱和土体导热系数,单位W·m-1·K-1;Ke为Kersten系数;1.33指的是形状参数;m是由砂粒含量确定的经验参数,对于砂粒含量大于40%的粗质土壤和砂粒含量小于40%的细质土壤,m分别取值为:0.96、0.27。λdry通过与孔隙度n线性关系拟合得到:
λdry=-a·n+b.
(12)
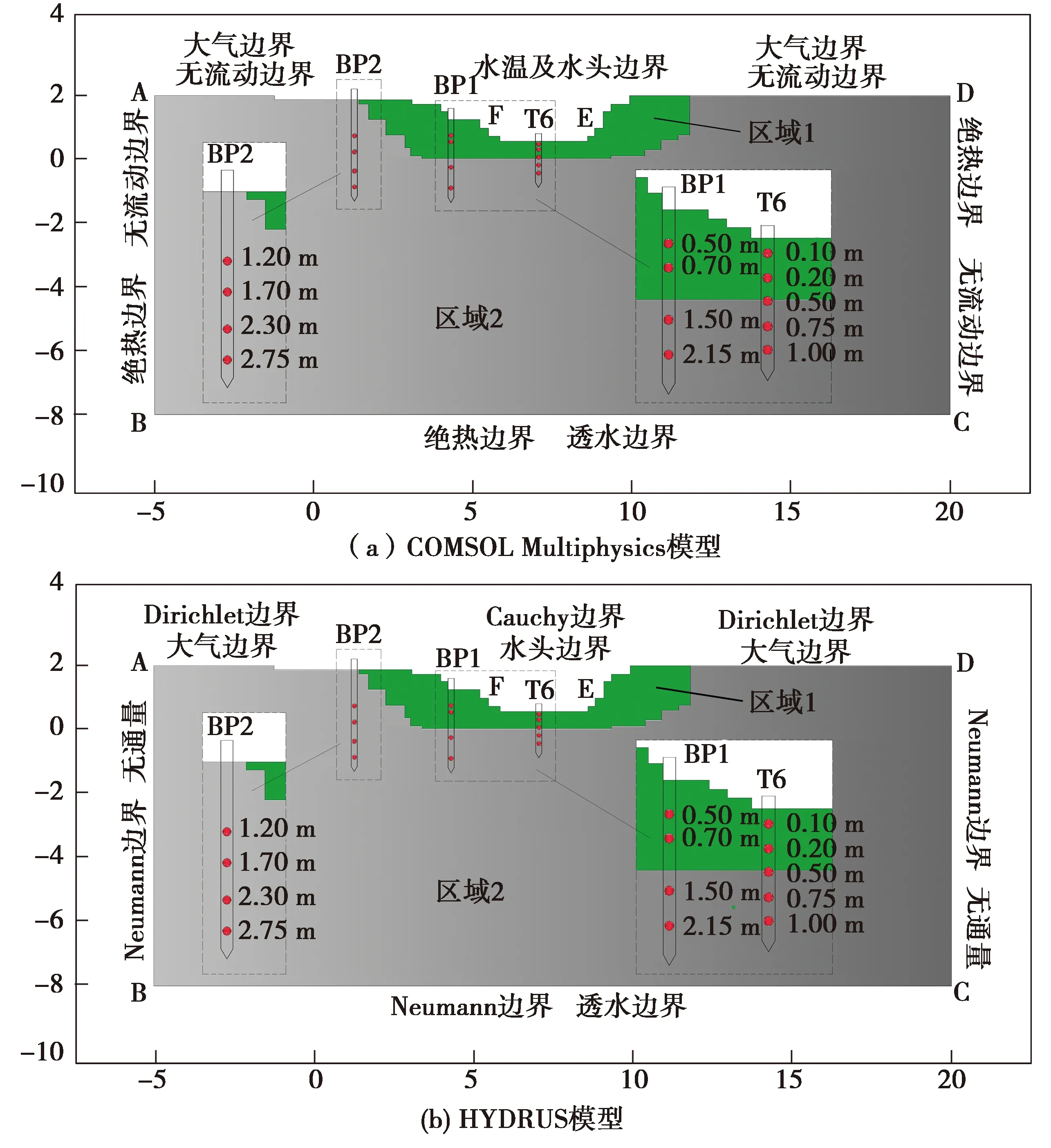
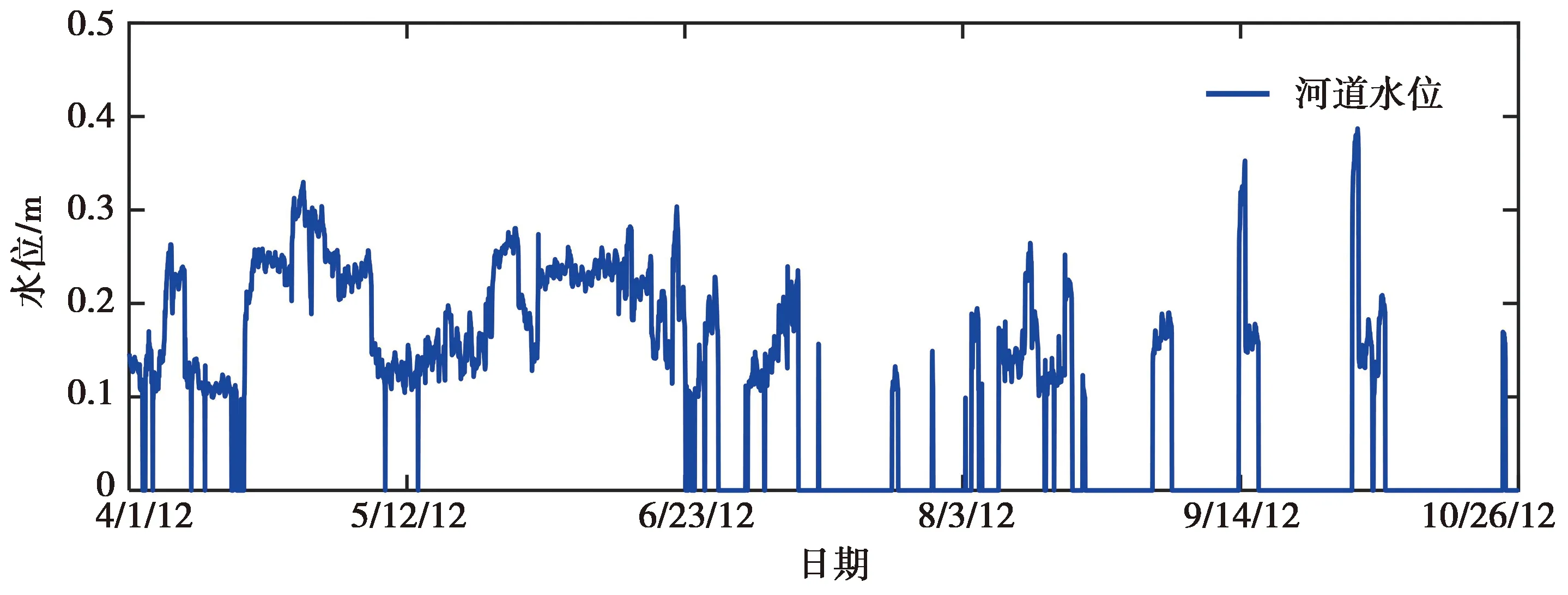
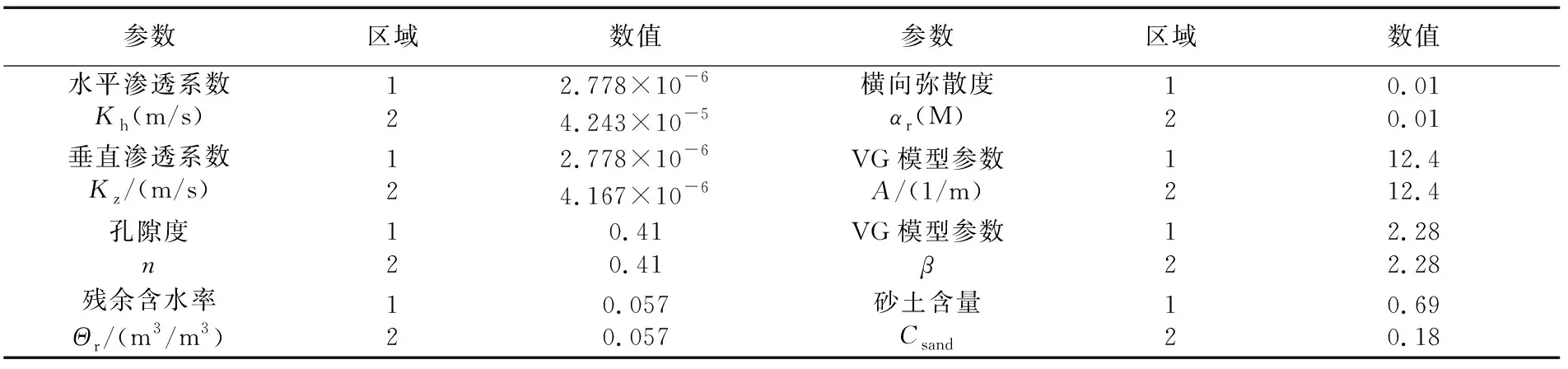
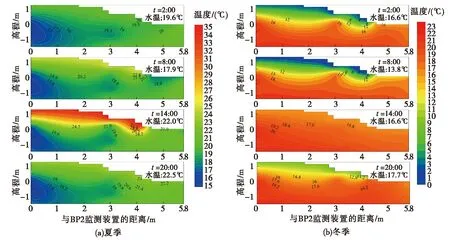
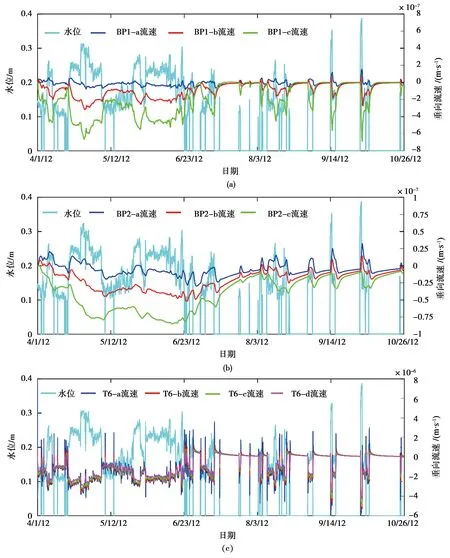
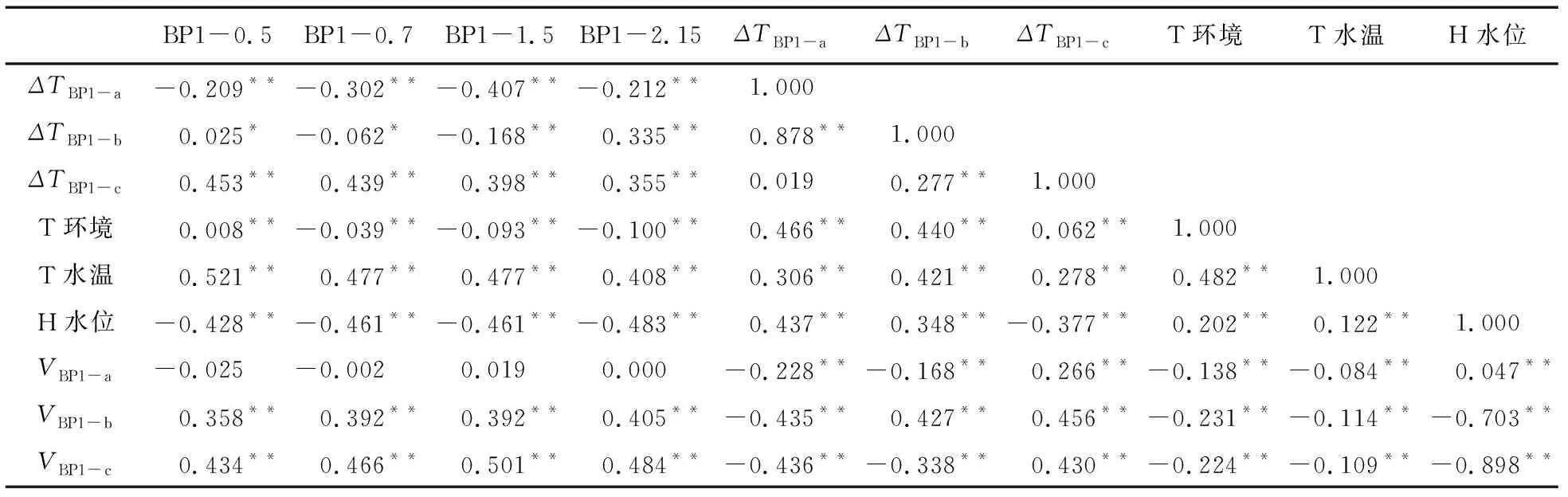
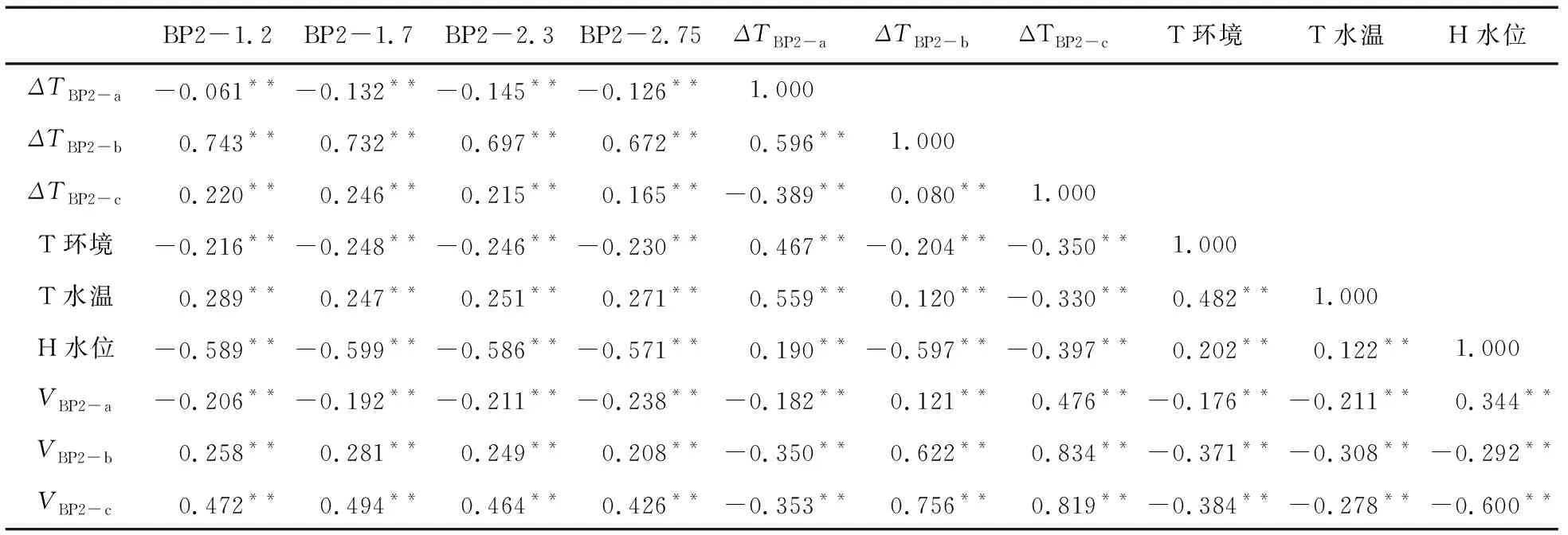
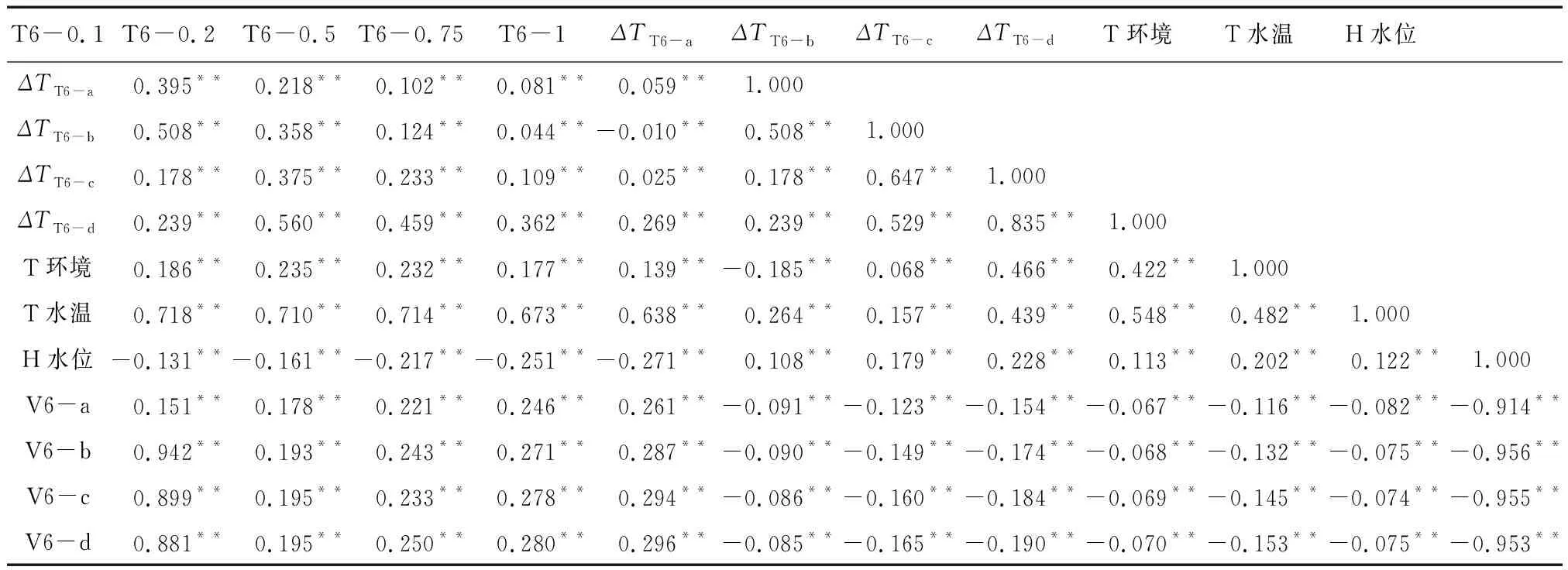
式中:a,b为经验系数;n为孔隙度,%。在0.2 饱和土体导热系数λsat的计算公式如下: (13) 1.3.3 Lu(2014)模型 Lu(2014)模型在Lu(2007)模型的基础上,进一步证实了土壤颗粒成分对λ的影响,模型公式简单,参数易于获取,但是对于干燥土体的导热系数只是粗略地通过线性拟合得到,没有全面考虑不同土壤质地,从而产生误差,模型精度有待进一步提高。模型公式如下[19]: λ=λdry+exp(φ-θ-τ),θ>0. (14) 式中:τ和φ是与砂粒含量、黏土含量、体积密度有关的λ(θ)曲线的形状因子。λdry采用Lu(2007)的关于n的线性方程(1-12)计算。 τ与黏粒质量分数Cclay满足如下关系: τ=0.67Cclay+0.24. (15) 参数φ具有以下多元回归方程,其值由砂土质量分数Csand和体积密度ρb确定: φ=1.97Csand+1.87ρb-1.36Csandρb-0.95. (16) 1.3.4 Ren(2019)模型 为了改变早期模型对土质的粗略划分,以及参数的不确定性,Ren等将早期模糊的参数取值改进为输入土体本身所拥有的精确物理参数。其次,考虑有机质含量对土体导热系数的影响,并且考虑土壤质地和颗粒组成对形状因子(表征导热系数增长速率和曲线斜率)的影响。在以往模型的基础上,采用Johansen(1975)的归一化模型,提出了在整个含水率范围内的新导热系数经验模型[20]: λ=(λsat-λdry)·Ke+λdry. (17) λsat=0.53Csand+0.1γd. (18) λdry=0.087Csand+0.019γd. (19) λsat和λdry与砂土含量和干土容重(γd)有关,当砂含量0 γd=g·ρb (20) 式中:g= 9.8 m2·s-1,是重力加速度。 Ke与θ的新关系如下: Ke=exp(α-θ-β). (21) α和β是λ(θ)曲线的形状因子,其值会影响到导热系数曲线的斜率和增长速度,表达式如下: α=0.493Csand+0.86Csilt+0.014Com+0.778. (22) β=0.736Cclay+0.006Com+0.222. (23) 式中:Cclay、Csilt、Csand分别为黏粒、粉粒、砂粒的质量分数(%);Com为有机质质量比(g·kg-1)。 采用均方根误差(root-mean-square error,RMSE)、决定系数(coefficient of determination,R2)和相对误差(relative error,Re)对模型的模拟精度进行评估。 (24) (25) (26) 引用美国地质勘探局于2012年3月至2013年10月在沃克河流域的实地研究项目,选取梅森谷的福克斯灌渠2号监测点的资料进行分析[31],该监测点位于38°54′06″N,119°09′30″E,海拔约为 1 354.45 m。渠道水位和水温分别采用Micro-Diver型压力传感器和温度自动监测仪进行测量,测量精度分别为±1.0 cm和±0.1℃,分辨率分别为0.2 cm和0.01℃。各监测井分别位于河道中心位置0 m、2.8 m和5.8 m处。各监测井传感器距离地表位置分别为T6(0.1 m、0.2 m、0.5 m、0.75 m、1 m),BP1(0.50 m、0.70 m、1.50 m、2.15 m),BP2(1.20 m、1.70 m、2.30 m、2.75 m),各数据每间隔1 h记录一次。 2.2.1 边界条件 本研究选取福克斯灌渠在2012年4月1日至2012年10月26日的温度和水位实测数据进行分析,依据土壤物理特性将研究区域划分为区域1和区域2。区域1和区域2的初始温度取监测数据第一个星期的平均温度,分别为6.6 ℃和6.25 ℃。 在COMSOL Multiphysics建模中,模型边界条件及尺寸如图1(a)所示。对于温度场,将两边AB、CD以及底部BC均设置为绝热边界,河道中与水流接触的EF为水温波动边界,最高水位之上与大气接触的AF和ED设置为气温波动边界,由于大气温度及水温是随时间变化的温度序列,故采用三次样条插值函数施加在边界上,图2是2012年4月1日至2012年10月26日的气温与水温实测数据动态变化图。对于渗流场,水位之上AF、ED以及断面左右两边AB边界和CD边界均为无流动边界,底部BC为透水边界,EF设置为变水位边界,同样采用三次样条插值函数进行施加,河道水位数据如图3所示。 图1 模型计算区域及边界条件(单位:m)Fig.1 Model calculation area and boundary conditions 图2 气温与水温动态变化图Fig.2 Dynamic changes intemperature and water temperature 图3 河道水位时程曲线图Fig.3 Time-history chart of river water level 相比于COMSOL Multiphysics,在HYDRUS建模中其渗流场边界条件设置与COMSOL Multiphysics软件相同,这里不再赘述。热传导边界对最高水位至河床表面EF设置为第三类边界(Cauchy边界),即就是随时间变化的水温边界,这与COMSOL Multiphysics软件中的水温边界一致,都是插入实际水温值;AF和ED设置为第一类边界条件(Dirichlet边界),即就是指定温度边界,可插入实际大气温度;左右两边AB、CD以及断面底部BC设置为第二类边界条件(Neumann边界),即就是COMSOL Multiphysics软件中的绝热边界,具体设置如图1(b)所示。 2.2.2 模型参数 结合现场勘查资料并参考[31]野外试验相关数据,给出了饱和-非饱和流-热耦合模型渗流场及温度场的计算参数,其中渗透系数采用室内试验中的常水头法进行测量,土壤孔隙度通过环刀法测量,残余含水率通过烘干法测量,土壤粒径级配(PSD)采用移液管法测定[32],有机质含量采用Walkley-Black滴定法测量[33],水的比热容为默认值,各参数的具体数值如表1所示。 表1 河床、河岸带饱和-非饱和流-热耦合模型计算参数Table1 Calculation parameters of saturated-unsaturated hydro-thermal coupling model for riverbed and riparian zone 续表 图4和图5分别为各模型对3个监测井BP1、BP2和T6的13个监测点在2012年4月1日至2012年10月26日的5 000个小时的温度拟合效果图,表2为各模型对各监测点的拟合误差结果。 图4 各模型对BP1和BP2监测井的拟合温度曲线图Fig.4 The fitting temperature curve of BP1 and BP2 monitoring tube by each model 图5 各模型对T6监测井的拟合温度曲线图Fig.5 The fitting temperature curve of T6 monitoring tube by each model 表2 各模型对各监测点的拟合误差表Table2 The fitting error table of each model for each monitoring point 由图4、图5和表2可以看出,对于河道中心的T6监测井,越靠近河床表面,温度的正弦日变化越明显,温度波动越大,随着深度的增加,温度日变化减小,呈季节性周期变化。这可能是因为越靠近河床表面,其受水位变化以及大气温度变化的影响越明显。相比于T6监测井,距离河道中心2.8 m处的BP1监测井和距离河道中心5.8 m处的BP2监测井各点温度变化较为稳定,温度日变化不明显。 从拟合效果可以看出,相比于其他模型,基于COMSOL Multiphysics软件的Ren(2019)模型更适合应用于河床以及河岸带饱和-非饱和流-热耦合研究中,整体拟合精度较高,适用范围更广,能够较为精确地刻画饱和-非饱和温度场的动态变化过程。其均方根误差RMSE的变化范围在0.824~2.691°C之间,均值为1.539℃,明显小于其他模型,决定系数R2的变化范围在0.589~0.974之间,均值为0.851,相对误差Re变化范围在4.5%~15.5%之间,均值为8.6%,均优于其他模型;其次是Chung & Horton(1987)模型,均方根误差RMSE均值为2.010°C,决定系数R2均值为0.764,相对误差Re均值为11.1%,Lu(2007)和Lu(2014)模型拟合效果一般。 这是因为有研究表明有机质含量也会影响土体的导热系数[34],有机质含量增加了土体的疏水性[35],即就是改变了土壤中的水分分布,从而影响土的导热系数。而Ren(2019)模型相比于其他模型考虑因素更加全面,其不仅考虑了有机质含量对导热系数的影响,同时也考虑了土壤质地对用来表征导热系数增长速度和曲线斜率的形状因子的影响;相比于Ren(2019)模型,Chung & Horton(1987)模型只考虑了含水率对导热系数的影响,因此在土壤其他物理参数发生变化的情况下,模拟误差就会较大;Lu(2007)将土体大致分为粗质土壤和细质土壤,引进一个与砂粒含量相关的经验常数,但由于没有定量或定性的区分土质,导致计算时对该常数取值不易确定,从而产生偏差,Lu(2014)模型[36]对于干燥土体的导热系数只是粗略地通过线性拟合得到,没有全面考虑不同土壤质地,因此误差仍然很大。 为研究温度在河床以及河岸带剖面的空间分布规律及动态变化特征,根据上述已验证的河床及河岸带饱和-非饱和流-热耦合模型,通过比较2012年 6 月 22 日和2012年10月5日不同时刻的温度云图,发现在该时间点研究区域分别符合季“上暖下凉”,冬季“上凉下暖”的温度时空分布规律,为了进一步表明变化的趋势和规律,选取6月22日和10月5日为典型时间点进行分析。在t= 2:00、t= 8:00、t= 14:00和t= 20:00四个不同时刻模拟数据,绘制不同季节河流横断面的温度日变化云图,如图6所示。所选区域从地表面开始,同时包含了3个监测井的所有监测点,横轴表示距离BP2监测井的距离,纵轴表示高程。 图6 不同季节河岸带温度变化特征Fig.6 Characteristics of temperature change in riparian zone in different seasons 由图6(a)可知:在夏季总体上呈现表层 > 中层 > 底层的趋势,河床、河岸带温度大致可分为低温区、中温区和高温区,即在远离河道的浅层区域温度较高,河岸带深层区域温度较低。通过比较6月22日不同时刻的温度云图发现:1) 在t= 2:00至t= 08:00时段内,气温逐渐上升,使得河岸带地表温度随之升高,而河床温度相对较低,这种现象同样出现在Ren等[37-38]的研究中,这是由于此阶段河流水位上升,达到一年内最高水位,水温相对较低导致;2)在t= 8:00至t= 14:00时段内,太阳辐射作用逐渐增强,河岸带沉积物因比热容相对较低,表层温度迅速上升,与河道水温形成高温度差,河岸带内的垂向温度分层明显,表层温度明显高于中层和底层;3)当t= 20:00时,整个研究区域低温区面积逐渐增大,高温区面积开始减小,由于空气和水二者热容相差较大,因此河岸带沉积层温度降低较快,而河床部分温度相对稳定。 由图6(b)可以看出:在冬季总体上呈现表层 < 中层 < 底层的趋势,河床、河岸带温度大致也可以分为低温区、中温区和高温区,然而与夏季相反,低温和中温区域主要保持在河岸带浅层区域,而河床内部与河岸带深层区域温度分布相对均匀。通过比较10月5日的四个不同时刻发现:1) 在t= 2:00至t= 8:00,河床、河岸带温度分布相对均匀,受夜间温度影响,河岸带表层温度较低,而河床区域温度相对较高且比较稳定;2)在t= 8:00至t= 14:00,整个研究区域温度较之前升高,变化最为明显的是河岸带表层区域;3)当t= 20:00时,由于环境温度的逐渐减小,河岸带浅层温度逐渐降低,但河道水温因滞后以及比热容较大的原因,并未立即降低,整体温度场分布逐渐恢复至t= 2:00时的状态。 通过上述分析可以看出,季节性温度变化以及水位对河床、河岸带的温度场影响较大,在同一季节,河岸带表层沉积物的温度变化较为显著,深层区域相对稳定,这是因为超过地表以下1 m深度的土壤对大气温度以及太阳辐射不太敏感,温度的年波动最多可延伸至地表以下10 m[39],此外Engelhardt等[40]研究表明,昼夜温度变化作用对较深层的潜流带温度作用不明显,这一点也被Lee等[41]的研究所证实。因此更加说明利用COMSOL Multiphysics软件建立的基于Ren(2019)模型的饱和-非饱和流-热耦合模型是可靠的。 基于上述验证后的饱和-非饱和流-热耦合模型,反演推算出流速场信息。图7为河床以及河岸带内部流速场随水位波动发生规律性变化图。文中给出T6,BP1,BP2监测井中两两监测点中心位置的垂向流速,即T6-(a,b,c,d)、BP1-(a,b,c)和BP2-(a,b,c)。当水位上升时,负值表示地表水补给地下水,正值表示地下水补给地表水。由图7可以看出,不同监测井不同深度处的流速在时间和空间上都有很大的差异。对位于河岸带上的BP1和BP2监测井,监测点越靠近河床表面,流速波动范围越小,流速值随水位上升增长较慢,且流速较小;水位下降,流速朝相反方向变化,地下水补给地表水,但补给速度仍然较小,整个监测过程中流速有正有负(BP1-a和BP2-a)。而随深度的增加,流速波动范围增大,随水位上升,流速迅速朝负方向增大,流速值较大,且流速主要以负值为主,呈现出地表水补给地下水的现象。 图7 各监测井不同深度流速与水位关系图Fig.7 Diagram of relationship between flow velocity and water level at different depths of each monitoring tube 而位于河床中心的T6监测井则呈现出与河岸带监测点相反的趋势。具体表现为,离河床越近,流速随水位波动就越大,流速值越大,随着监测点深度的增加,流速波动逐渐减缓。但与BP1和BP2监测井同样,在浅层区域,流速有正有负;随深度增加,流速主要以负方向为主,即主要为地表水补给地下水。 表3是3个监测井各自不同影响因素之间的相关矩阵与显著性分析,由表3可以看出: (1)BP1监测井浅层区域温差(ΔTBP1-a,ΔTBP1-b)与BP1各监测点温度呈弱负相关,而深层区域温差(ΔTBP1-c)与各监测点温度近似呈中度程度正相关,对于BP2监测井,其浅层区域温差(ΔTBP2-a)与BP2各监测点温度同样呈弱负相关,随深度增加,转化为正相关,达到弱正相关和中度程度正相关的范围。而对于T6监测井,可明显看出,其各区域温差与各监测点温度均呈正相关,因此可以推断,各区域温差与各监测点的相关性可能受地下水位影响,与该区域距离河床或者地下水位的距离有关。 (2)环境温度与BP1、BP2监测井的各监测点温度均为弱负相关,而与T6监测井的各监测点温度随深度呈消减式弱正相关,这是因为,监测点埋置在地表以下,即使气温波动较大,但因为“衰减”和“滞后”效应,位于河岸带内部的监测点温度波动幅度仍相对较小,所以呈现出弱相关,这也体现了河床、河岸带夏季“上暖夏凉”,冬季“上凉下暖”的温度分层现象。 (3)水温与T6监测井各监测点温度呈强正相关,与BP1各监测点温度呈中度程度正相关,与BP2各监测点呈弱正相关,由此可以看出,距离河床越近,其温度场受河水影响越大。 (4)水位对距离地表较近的浅层区域流速影响较小,而对深层区域流速影响较大,呈强负相关;水位升高,地表水开始补给地下水,流速逐渐减小并朝负方向增大。 (5)水位与河岸带区域的BP1各监测点的温度均呈中度程度负相关,与BP2各监测点温度同样呈中度程度负相关,与T6各监测点的温度呈弱负相关,相比于河床附近的监测点,水位对距离河床较远的监测点的温度影响更大,这与水温对各监 测井的温度影响恰恰相反。 (6)对于河岸带浅层区域,垂向流速与流速点所对应的区域温差呈弱负相关,随深度的增加,垂向流速与温差逐渐呈正相关,且相关性逐渐增大。而对于河床中心的T6监测井,其各点垂向流速与流速点所对应的区间温差呈弱负相关,由此可以看出,温度梯度会引起水体流动,水体流动又会导致温度变化,且该现象对于河岸带深层区域较为明显。 (7)对于河岸带区域,除了离地表较近的监测点以外,随着深度的增加,流速与监测点温度的相关性由弱正相关增强到中度程度正相关,随着地下水流速的增大,各监测点温度也随之增大。而对于T6监测井,其各中心点流速与其他各监测点温度几乎都呈弱正相关,相比于河岸带,流速的变化对各监测点温度的影响较小。另外,从表3还可以看出,环境温度和水温与 BP1、BP2和T6各监测点流速均呈弱负相关,有一定的抑制作用。 表3 各监测井中各影响因素之间的相关矩阵与显著性分析Table3 Correlation matrix and significance analysis of each influencing factor in each monitoring tube (a) (b) 本文通过运用两款商业软件嵌入四种土体导热系数模型,基于内华达州梅森谷的福克斯灌渠2号监测点的数据资料,分析了不同模型对河流潜流带温度场的模拟效果: (1)相比于基于HYDRUS软件的Chung & Horton(1987)模型以及基于COMSOL Multiphysics软件的Lu(2007)、Lu(2014)模型来说,基于COMSOL Multiphysics软件的Ren(2019)模型更适合应用于河流潜流带的饱和-非饱和流-热耦合研究中,模型考虑因素更加全面,使得整体拟合精度较高,适用范围更广,能够较为精确地刻画饱和-非饱和温度场的动态变化过程。 (2)水温以及地表以下各监测井的温度相比于环境温度具有明显的“衰减”和“滞后”现象,环境温度的日变化对河床区域的温度场分布影响较大,而对河岸带区域影响较小,距离河床越远,埋置深度越深,受大气温度与水温的影响就越小,温度场变化越稳定。 (3)对于河岸带区域,随着深度增加,流速与其上下两个监测点以及两点温差逐渐由极显著弱相关变为极显著中度程度正相关,与水位呈极显著负强相关,且越靠近河床,其相关系数越大,即随深度增加河岸带受侧向潜流交换以及地下水影响增大;且各监测点温度与水位呈极显著中度程度负相关。对于河床区域,各测点温度受水温影响较大,呈极显著强相关;流速与水位呈极显著极强负相关。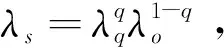
1.4 模型评估
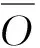
2 实例应用
2.1 研究区域概况
2.2 模型边界条件与参数设置


3 结果与讨论
3.1 模型对比分析
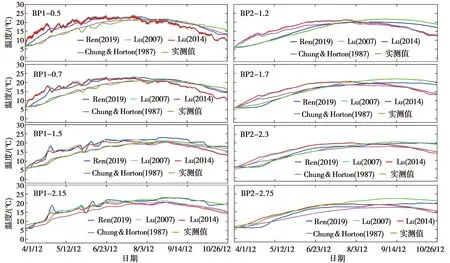
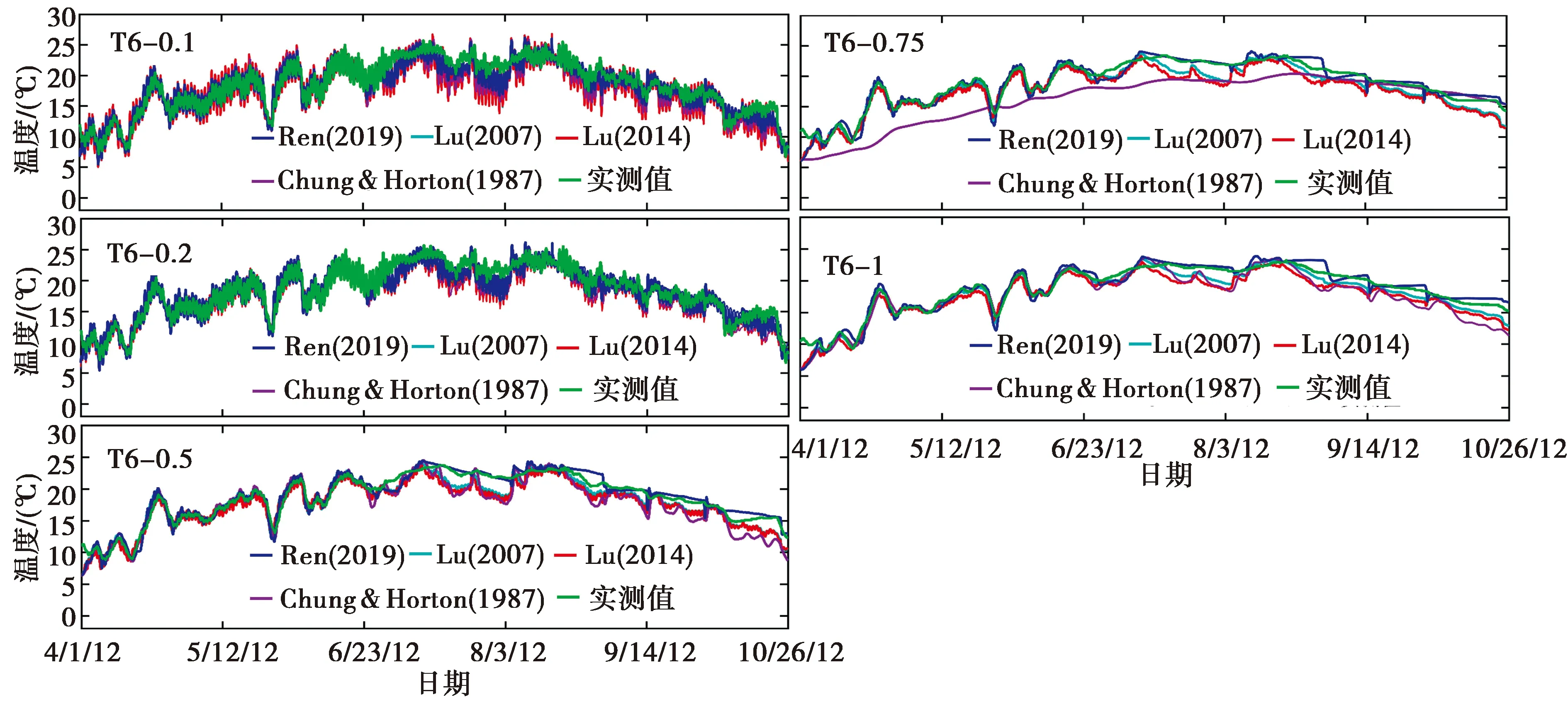
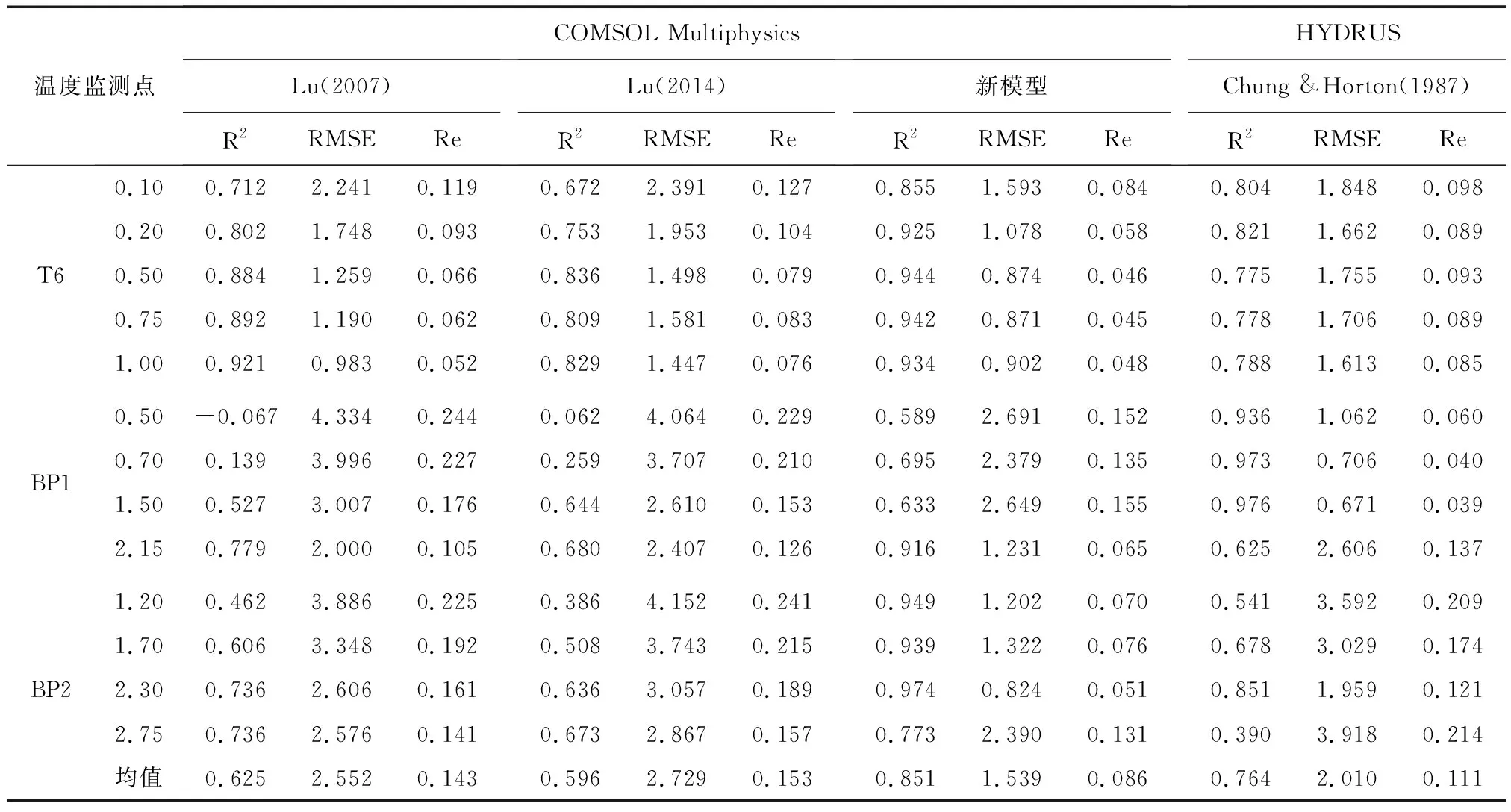
3.2 河床、河岸带温度场的时空分布规律
3.3 流速空间变化规律分析
3.4 相关性分析
4 结论
