垂直节理对黄土边坡稳定性影响分析

2021-12-21王丽丽

自然灾害学报 2021年6期

王丽丽，李宁

(1.西安理工大学岩土工程研究所，陕西西安 710048； 2.中国地震局(甘肃省)黄土地震工程重点实验室，甘肃兰州 730000；3.兰州交通大学土木工程学院，甘肃兰州 730070)

黄土属于第四纪沉积土，黄土地层自上而下是非均质和各向异性的，涵盖各种古土壤层、钙质结核、孔洞(包括陷穴)、裂隙、节理等，其中，黄土节理在黄土地层中发育极为普遍，特别是垂直节理，是构成黄土的主要特征之一[1-3]。调查发现，在斜坡后缘、塬边位置以及靠近临空面的土体内存在大量垂直节理和裂隙[4-6]，有研究认为，很多黄土滑坡后缘陡坎受垂直节理控制，陡坎被认为是黄土垂直节理张拉破裂面[7-9]。黄土节理的存在，一方面相当于对边坡进行了分割，降低了边坡的整体性，增大了黄土的各向异性[10]，另一方面，黄土地区常年干旱少雨，大部分的黄土平时处于低含水率状态，在降雨来临时，垂直节理成为了渗流优势面[11]，为降雨通过浅表黄土通向深部黄土下渗提供了通道[12-13]，同时节理面的抗剪强度和抗拉强度降低，土体自重增大，边坡的稳定性随之降低，可进一步的导致湿陷性极强的黄土边坡发生失稳[14-15]。第三，闭合型垂直节理在卸荷作用、湿陷作用以及降雨入渗下会进一步扩展为张开型节理与地裂缝[16]，进一步提高了滑坡的发生概率。因此黄土中的竖向节理是影响黄土边坡稳定性不可忽视的重要影响因素，研究含垂直节理黄土边坡的稳定性具有重要意义。

现阶段对含垂直节理边坡稳定性的研究主要以数值模拟计算与野外实地勘察为主。如：毛举等[4]采用扩展有限元法研究了垂直节理长度与距坡面水平距离对边坡稳定性的影响，认为在距坡面5 m～9 m 范围之内垂直节理对边坡的影响达到最大，深度超过 12 m 后影响可忽略不计。杨阳等[17]、马鹏辉等[9]考察泾阳南塬黄土滑坡后提出湿陷性竖向裂隙距离塬边的距离为15 m～30 m，卸荷竖向裂隙距离塬边的距离不超过7 m。实际上，原状黄土中不仅存在垂直节理，更存在大量的不同倾角的斜节理，孙萍等[18]通过黄土的三轴压缩试验研究了0°～ 60° 4 种不同倾角的裂隙性原状黄土的力学特性，认为土体破裂面会受原有节理裂隙面影响。

因此，在研究垂直节理影响下的边坡稳定性时，垂直节理的存在对边坡滑动面的位置和破坏模式是否会产生影响以及影响范围应该是研究垂直节理对边坡稳定性影响需要重点解答的问题。对垂直节理的研究需要在通过室内试验探究含垂直节理试样的破裂破坏特点，尤其是破裂面的走向的基础上，建立垂直节理与斜节理同时存在于边坡内部的数值模型，计算节理面的存在对边坡滑动面的位置以及破坏模式的影响。

本文通过室内三轴试验，研究了节理性黄土试样的破坏特点与力学特性，在此基础上建立有限元模型，计算了垂直节理的长度效应、临坡距离效应与倾角效应，提出了垂直节理的失稳破坏特征，并进行了理论推导和验算。图1展示了黄土边坡垂直节理的分布情况，图2为降雨沿垂直节理面的入渗情况。

1 室内试验材料与制样方法

研究垂直节理试样的力学变化规律对于了解边坡后缘拉裂演化过程、垂直节理对边坡滑动面的影响具有重要意义。试验用黄土取自甘肃省岷县永光村，试验结果显示，其天然含水率为6.3%，塑限为17.83%，液限为23.33%，最优含水率为16.5%，最大干密度为1.68 g/cm3。

笔者曾讨论过一种节理性土工三轴试验制样的方法[19]，以此制作含不同倾角的节理性三轴试样，并对此方法下节理试样的强度与破坏形式与原状节理试样进行了比对和探讨，在此基础上，为了分别模拟不同张开程度节理试样的力学特性，分别制作了闭合型与张开型2种垂直节理试样：张开型节理试样在制作时配合图3(a)的击实块，试样分两部分制作，每部分分层击实，制作完成后两部分拼接形成如图3(b)所示的张开型垂直节理试样；闭合型节理试样采用文献[19]的方法，对节理面进行刮毛后增设隔离材料，形成图3(c)闭合型垂直节理。

图3 两种不同粘结程度的垂直节理试样Fig.3 Two kinds of vertical joint simples with different bonding degrees

同理，配合如图4所示的不同倾角的击实底盘，制作了含不同节理倾角的三轴试样，如图5所示。定义节理倾角β：水平方向与节理面间的夹角。

图4 不同节理倾角底盘Fig.4 Chassis of sampler with different joint dip angle

图5 不同β倾角的节理性三轴试样Fig.5 Triaxial samples with differentβdip angle

2 室内试验结果分析

2.1 垂直节理的强度与破坏特点

试样含水率w=10.0%，密度ρ=1.69 g/cm3。对试样的典型破坏方式及应力-应变关系进行探讨如下。

图6为2种节理试样以及无节理的空白样的无侧限抗压强度试验典型应力-应变曲线，图7为对应的破坏图。

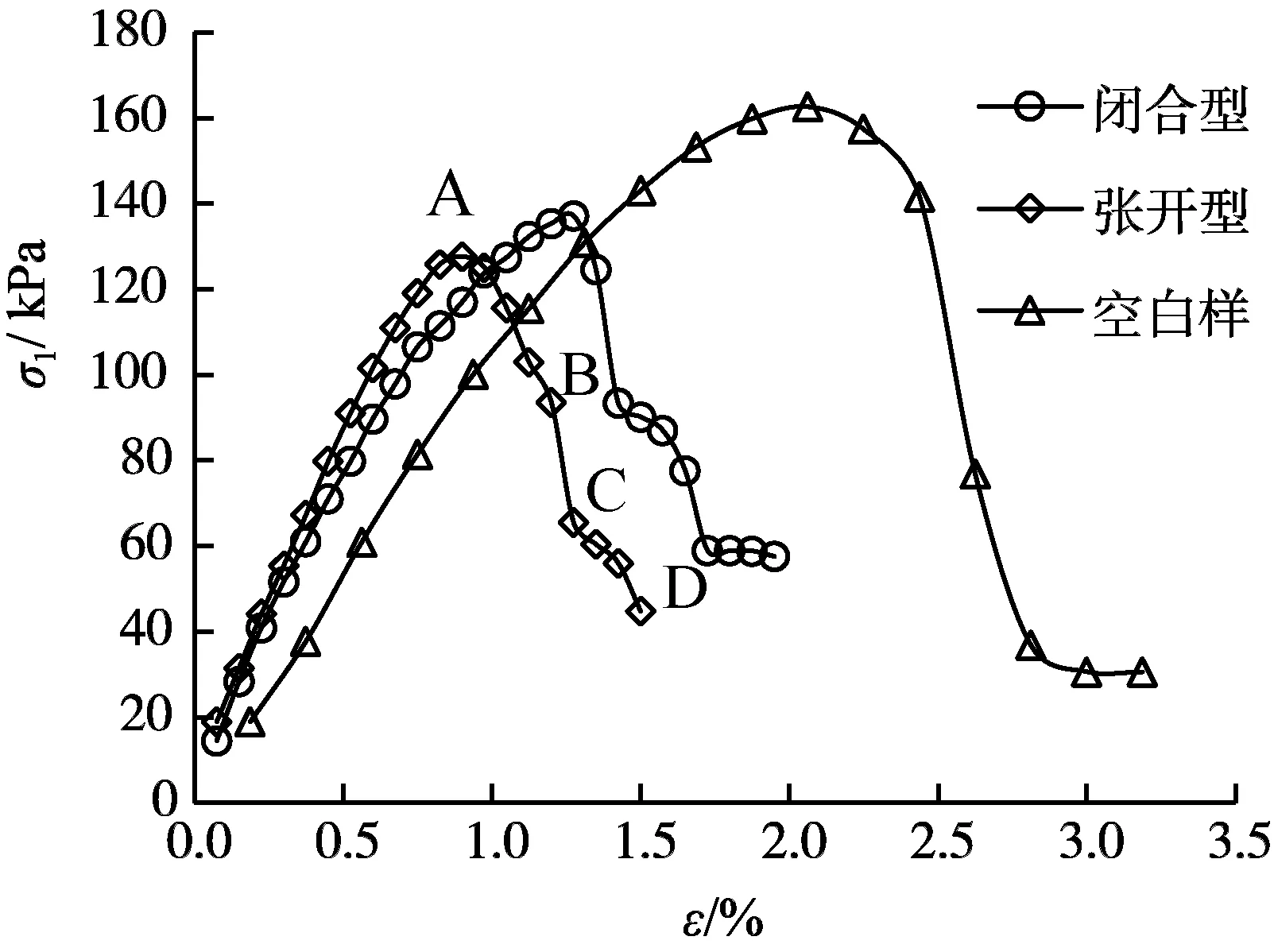
图6 无侧限抗压试验应力-应变曲线Fig.6 The unconfined compressive strength stress of vertical jointed specimens

图7 垂直节理性试样无侧限抗压破坏图Fig.7 The failure characteristics of unconfined compressive of vertical jointed specimens

分析2种不同节理性试样强度特点知，闭合型强度略大于张开型强度，闭合型垂直节理试样和张开型垂直节理试样强度相较于无节理试样分别降低15.7%和21.5%。从峰值强度所对应的应变分析试样的破坏速率可知，张开型试样破坏速率大于闭合型试样。

从试样的破坏过程和破坏方式来分析上述强度和破坏差别的原因：

首先，对比分析闭合型与张开型2种试样的破坏知，闭合型节理试样，先发生剪切破坏，由于垂直节理的存在，剪切破坏面发展至节理处时，垂直节理面部分张开，并与破坏面连接贯通。破裂面与节理面贯通后，若垂直节理面全部张开，则形成图7(b)所示破坏，剪切破裂面倾角β= 65°～68°；若垂直节理面部分张开，则形成图7(a)所示破坏，剪切破裂面倾角β= 41°～58°。

张开型节理试样的破坏与闭合型类似，首先发生剪切破坏，但是由于节理是完全张开的，在破裂面经过节理面时与节理面完全贯通，其破坏与闭合型的破坏2类似，剪切破裂面倾角β= 68°。由于闭合型试样节理面有一定黏结强度，其均匀性和整体性优于张开型试样，因此强度也略大于张开型。

对图6峰值后应力应变曲线进行划分为3个阶段：A-B段为试样发生初次剪切破坏阶段，B-C段与C-D段的多次应力跌落说明试验在峰值后经历了多次的张拉脆性破坏[20]，可对应试样的多个剪切破裂面、垂直节理面的张拉贯通等。

总结垂直节理的强度与变形破坏特点知：强度上，闭合型略大于张开型；破坏速率上，张开型大于闭合型；在破坏特点上，2种节理型试样都经历了“剪切破坏-剪切破裂面与垂直节理面贯通-残余变形”三个阶段；闭合型垂直节理在一定外力作用下可以转化为张开型垂直节理，验证了冯立等[5]关于黄土垂直节理发育机制的观点。

三轴压缩试验采用了3种围压，分别为50 kPa，100 kPa，150 kPa。对3种围压条件下含闭合型垂直节理试样的应力应变曲线与典型破坏状态总结如下。

分析图8与图9知，随着围压的增大，应力应变曲线逐渐表现为应变硬化型，试样的破坏也表现为典型的剪切破坏特点，这说明垂直节理的存在对强度和破坏形态的影响逐渐减小。同理可推测，在边坡中的随着侧向的约束作用的增大以及埋深的增加，竖向节理对边坡稳定性的影响会逐渐减小。

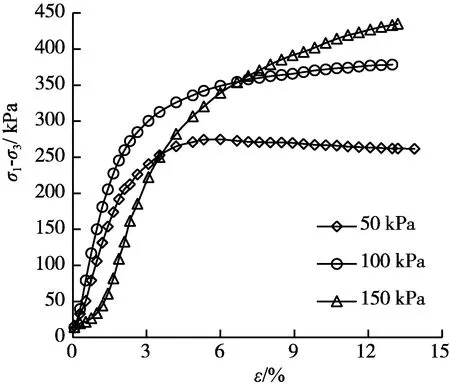
图8 不同围压条件下含垂直节理试样应力应变曲线Fig.8 Stress strain curves of samples with vertical joints under different confining pressures

图9 三轴压缩试验垂直节理试样典型破坏图Fig.9 The typical failure diagram of vertical joint samples in triaxial compression test

2.2 斜节理试样的强度与破坏特点

对节理倾角为0°～90°间的6种倾角试样进行了无侧限抗压强度试验与三轴压缩试验，每种倾角节理都采用了3组以上的平行样进行测试，对试样的强度与典型破坏特点进行了总结分析。

无侧限抗压强度试验表明：斜节理试样的破坏主要有沿节理面的滑动破坏、节理面与剪切破裂面呈 X型的共轭剪切破坏、滑动+剪切破坏、节理面与破坏面斜交破坏，共4种典型破坏类型，各典型破坏图如图10所示。

图10 不同倾角斜节理试样典型破坏图Fig.10 The typical failure diagram of joint samples with different dip angle

其中，“沿节理面滑动破坏”主要发生在β倾角为45°～ 70°的节理性试样，且β=57°时3组平行样全部为沿节理面的滑动破坏；“滑动+剪切破坏”主要集中在β=45°时，剪切破坏的同时伴随着沿节理面的滑动破坏；“斜交破坏”与“X型共轭剪切破坏”在节理倾角较大的时候居多，试验中节理面间无相对滑动。

对不同节理倾角节理试样的无侧限抗压强度分析如图11所示。无侧限抗压强度随倾角β的增大呈先减小后增大的变化趋势，垂直节理与水平节理的存在对试样的抗压强度影响较小，节理倾角α=70°附近时，抗压强度最小。

针对时无侧限抗压试验表现出的特殊的沿节理面滑动特性，对不同围压条件下的节理试样应力应变曲线进行总结如图12所示，并与无侧限抗压强度45°试样的“滑动+剪切”破坏应力应变曲线比对分析。

总结图13滑动破坏的特点可知，滑动量随着围压的增大而逐渐减小，从图12可知，剪应力随着应变的增长呈现“增大-减小”的循环变化规律，且随着围压的增大，循环次数减少，直至在150 kPa作用下试样呈“应变硬化”型破坏。

图13 不同围压57°斜节理试样破坏图Fig.13 Triaxial compression failure characteristics of specimens with joint inclination equal to 57°

将50 kPa作用下57°试样与无侧限45°试样的滑动+剪切破坏过程进行分解，对应力应变曲线变化过程进行对应分析如下：

1)试样的压密、弹塑性变形阶段-剪应力增大阶段；

2)试样下半部分发生剪切破坏-剪应力差减小阶段；

3)沿节理面滑动，试样应力重分布，逐渐重新达到相对稳定状态，剪应力再次增大阶段。

在围压超过150 kPa后试样呈应变硬化破坏，不再沿节理面发生滑动，由此说明，在150 kPa的围压下，57°节理的存在对试样的力学特性影响已很小。黄土的天然密度介于1.5 g/cm3～2.0 g/cm3，按照σ3=Kρgh，侧向土压力系数K0对于可塑状态黏土可取0.53，则可反算埋深超过14 m后，57°节理的存在对于边坡的变形影响较小。

3 含垂直节理的黄土滑坡失稳的力学模型探讨

为探究含垂直节理边坡发生失稳时，边坡安全系数与垂直节理的长度、潜在滑动面倾角与长度间的关系，各设置含垂直节理的边坡模型示意图如图14所示，假设垂直节理的长度为h，距离坡面的水平距离为d，滑坡后缘剪切破裂倾角为β，圆弧滑动面简化为直线，长度为L。

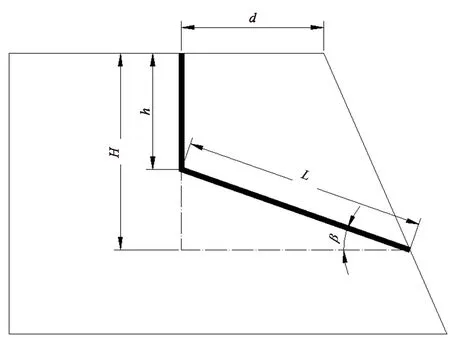
图14 解析计算示意图Fig.14 Schematic diagram of analytical calculation

假设垂直节理面的抗拉强度为σh，剪切破裂面的抗剪强度为：

τ=σtanφ+cl.

(1)

式中，φ为剪切破裂面的内摩擦角，cl为剪切破裂面的粘聚力。

滑面之上的梯形体总高度H可换算为：

H=h+Lsinβ.

(2)

滑面组合之上的梯形体重量：

(3)

根据安全系数的定义：

(4)

下滑力

Fs=Wsinβ-σhcosβ.

(5)

抗滑力

Ft=(Wcosβ+σhsinβ)tanφ+cl.

(6)

将式(5)式(6)代入式(4)得：

(7)

如果垂直节理面为张开型，或者抗拉强度σh极小，则：

(8)

将式(3)代入式(8)得：

(9)

如果垂直节理面为闭合型，抗拉强度σh较大不可忽略时，则：

(10)

综上所述，将含闭合型垂直节理和张开型垂直节理的边坡安全系数计算公式总结如下：

(11)

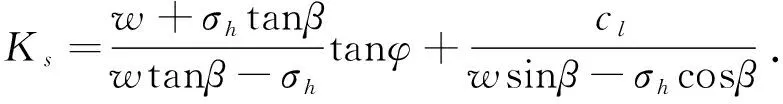
(12)

由此可知，含垂直节理的边坡稳定性的影响因素较多。总体而言，倾角β和长度L与边坡安全系数Ks呈负相关。垂直节理的长度h、距离坡面的水平距离d与Ks呈负相关，垂直节理的节理面抗拉强度σh与Ks呈正相关。

由此可知垂直节理的长度、临坡距离、滑移破裂面的倾角是影响边坡稳定性的主要因素，因此需要结合数值计算，进一步对节理边坡的稳定性进行进一步探究。

4 节理边坡的稳定性数值分析

首先，设置含不同长度与不同临坡距离垂直节理的边坡模型，研究仅含垂直节理条件下边坡极限状态下的主要塑性区分布与安全系数变化情况。在此基础上建立了含垂直节理与斜节理的边坡模型，对边坡的稳定性进行进一步分析，设置无节理的纯边坡模型作为对比参照。

4.1 垂直节理的长度效应与临坡距效应

模型高度为40 m，坡角为45°。垂直节理长度和距离坡肩的水平距离(后续简称临坡距离)分别为5 m、10 m、15 m和20 m。探究垂直节理尺寸和节理距离坡肩的距离对边坡稳定性的影响。节理面采用有限元“界面单元”模拟，通过增大法向刚度与切向刚度比来模拟节理面，法向刚度与切向刚度之比：kn/ks=100边坡土体与节理面的力学参数设置如下。

采用强度折减法计算边坡的稳定性，根据极限状态的塑性区等值线云图，以临坡距离d=15 m、垂直节理深度h=10 m为例，将等值线靠近坡顶边界定义为上滑面，将等值线底部边界定义为下滑面，将中部等值线的各峰值点连接后定义为主滑面，如图15所示，表1为模型的力学参数。

图15 边坡滑动面的提取与定义Fig.15 Extraction and definition of slope slip surface

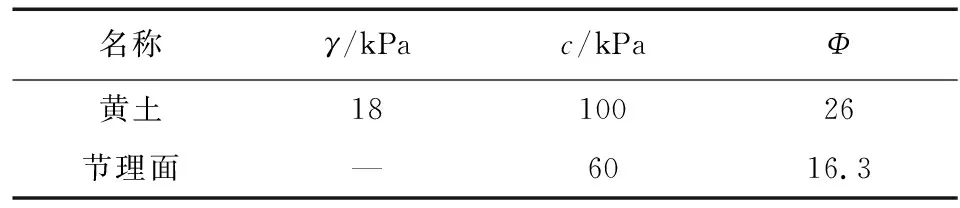
表1 模型力学参数Table1 mechanical parameters of the models

对各模型的主滑面分布以及塑性区等值线云图总结如图16所示。分析图16知，当节理长度h≤5 m时，垂直节理的存在以及临坡距离d的变化对于边坡滑动面形状和位置的影响较小，滑动破坏与无节理边坡相近。

图16 不同临坡距离模型主滑面分布图Fig.16 The distribution chart of main sliding surface with different slope distance models

当垂直节理长度h≥10 m时，节理的存在以及临坡距离的变化皆对滑动面的形状和位置产生了影响。边坡发生滑动破坏时沿节理面发生竖向的拉裂破坏，随着垂直节理长度的增加，竖向拉裂深度并未呈线性增长，竖向拉裂至10 m～12.5 m后拉裂深度不再随节理长度与临坡距离的增加而增大。除竖向拉裂部分外，滑动面的主滑面呈圆弧状，并逐渐与无节理影响边坡的主滑面重合。

从变形云图来看，垂直节理的长度h和临坡距离d对下滑面的影响较大，即对整体滑动范围影响较大：随着节理长度和临坡距离的增加，下滑面距离坡顶部自由面的距离逐渐增大，在d≥15 m，h≥10 m后，下滑面下穿到垂直节理底部为止。

对不同模型的安全系数提取如图17所示。由图17知，边坡的安全系数Fst随着节理临坡距离d的增长呈现先减小后增大的变化趋势，在d=10 m，h=15 m处达到谷值。2019 年 3 月 15 日省临汾市乡宁县枣岭乡山体滑坡后缘发现倾角约 80°的节理，此滑坡原始斜坡坡度45°，高度70 m，为典型的水致滑坡，垂直节理在滑坡产生的过程中起到了导水通道的作用。滑坡前缘与后缘之间的水平距离为15.9 m，与本文计算的坡度为45°，高度50 m的边坡相比，乡宁滑坡高度高，因此势能大，滑坡的范围比10 m略大。

图17 安全系数与临坡距离的变化关系Fig.17 Relationship between safety factor and slope distance

4.2 含垂直节理边坡的失稳滑移运动特征

室内试验与数值模拟皆得到了含垂直节理土体的破坏模式为“拉裂+剪切”破坏的结果，并且室内试验表明斜节理倾角β=45°～ 70°间时节理性试样可发生沿节理面滑动破坏，垂直节理试样的剪切破裂倾角为41°～68°。为了验证室内试验的单元研究结果在边坡模型中的合理性，并进一步的探究含垂直节理边坡的失稳滑移运动特征，揭示致灾机制，建立垂直节理长度分别为5 m、10 m、15 m、20 m，临坡距离为10 m，在垂直节理底部增设节理长度l=11.5 m，与水平向夹角β分别为30°，45°，57°，65°的斜节理，力求得到边坡后缘优势破坏倾角。

对各模型的主滑面以及塑性区等值线云图进行分析总结如图18所示。

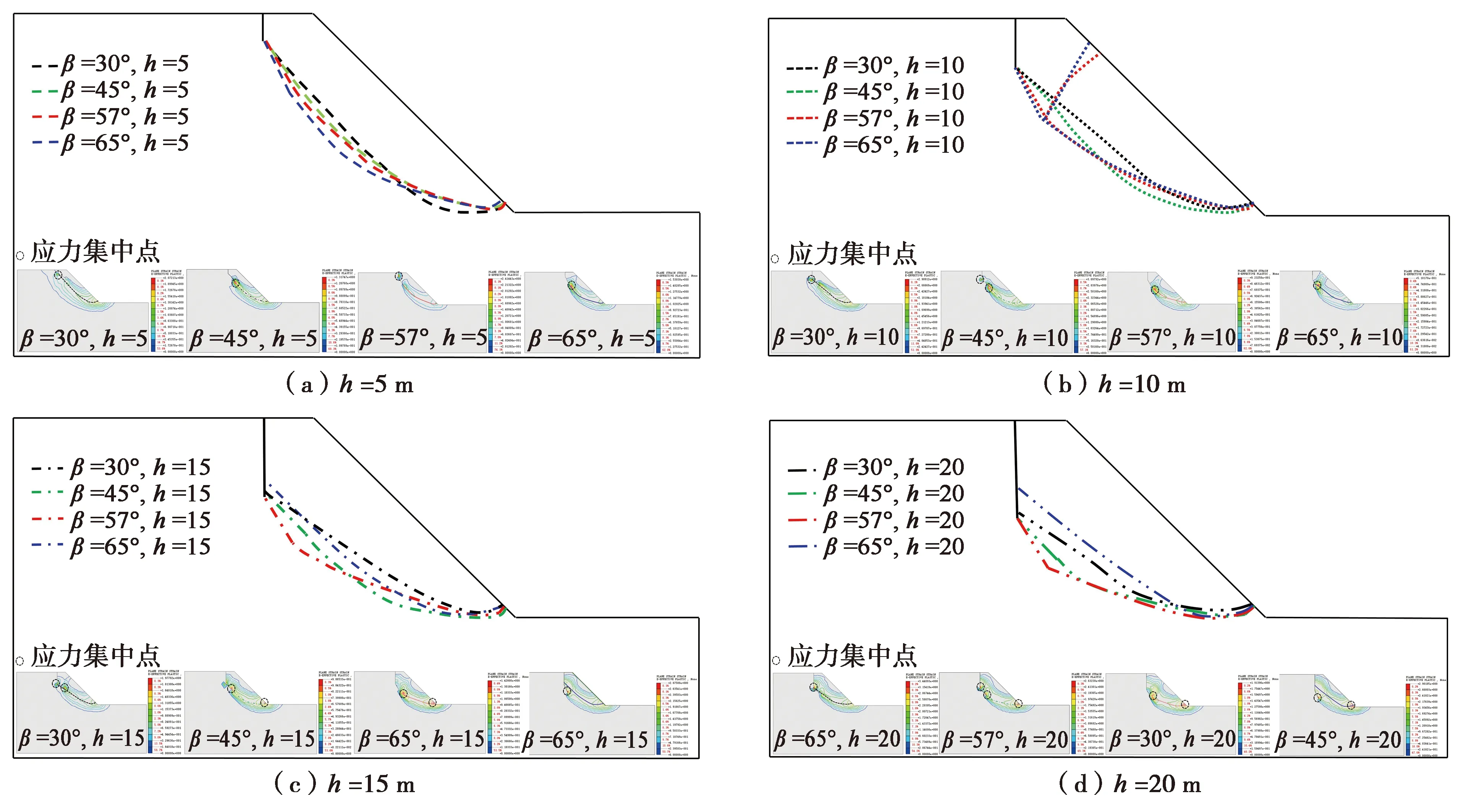
图18 不同倾角斜节理影响下的边坡主滑面与塑性区云图Fig.18 The slide surface and plastic zone of slopes with different joint dip angle

将图18中各模型的塑性区云图与最大剪应力云图进行了对比分析，其红色区域的位置是一一对应位置，因此在塑性区云图中对应力集中点进行了标记。分析应力集中点的分布知，应力集中点主要集中在垂直节理底部、斜节理顶部、底部以及边坡坡脚处，因此有发生沿垂直节理拉裂和沿斜节理滑动破坏的可能。具体分析如下。

分析主滑面随垂直节理长度与斜节理倾角的变化知：斜节理倾角β=45°与57°时，边坡沿斜节理面产生滑动破坏，边坡后缘拉裂长度与垂直节理一致。斜节理倾角β=30°与65°，垂直节理长度h≤10 m时，边坡主滑面穿越斜节里面，当h≥15 m时，边坡的滑动不再沿斜节理面，滑坡后缘的拉裂长度也不再与垂直节理长度一致。

对各模型的安全系数进行了统计分析，如图19所示。分析图19：1)h=10 m、β=57°与65°时，边坡的安全系数最低，结合图17(b)的主滑面分布知，在此条件下边坡除发生沿斜节理面的滑动破坏外，还可发生沿边坡中上部的拉裂破坏，滑坡的滑动概率增大，因此安全系数最小。2)数值计算的结果与室内试验得到的“β=57°时，试样表现为低强度和沿节理面发生滑动破坏特性”结果一致，因此边坡后缘优势破坏倾角为57°。

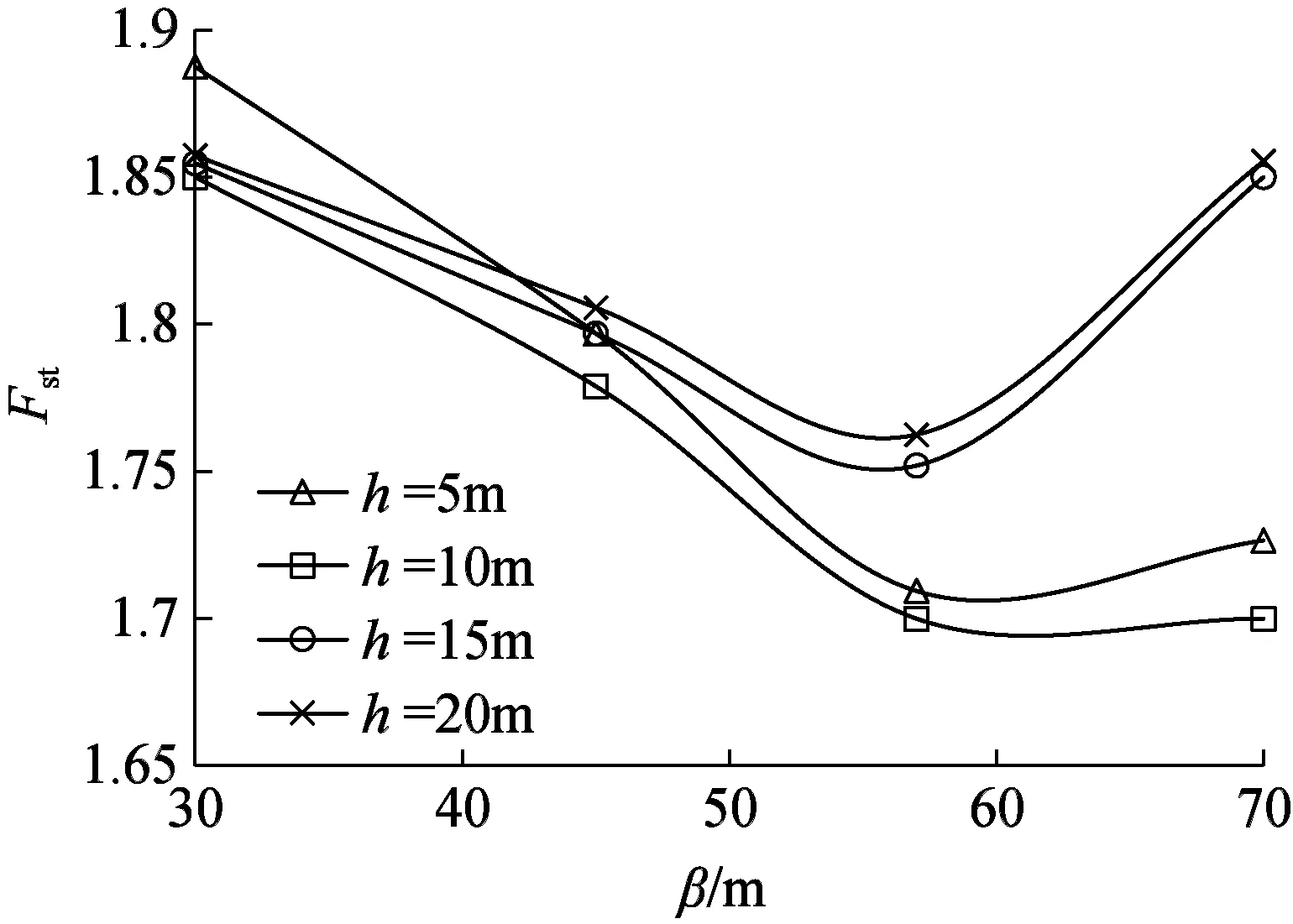
图19 边坡安全系数随节理倾角与长度的变化曲线Fig.19 The relationship between the slope safety factor and the joint dip angle

结合解析计算结果可知，实际上，含垂直节理的黄土边坡后缘剪切破坏倾角β、垂直节理的长度h、距离坡面的水平距离d对边坡的稳定性的影响都存在极值。将含垂直节理边坡的滑移特征总结如下：含垂直节理的黄土边坡，破坏时先沿垂直节理发生拉裂破坏，拉裂的深度与垂直节理的长度有关，垂直拉裂最大可达12.5 m，拉裂后缘的最优破坏倾角为57°。