含软弱夹层的顺层岩质滑坡渐进破坏研究

唐雨生，苏培东，马云长，戚宗轲

(1.西南石油大学 地球科学与技术学院, 四川 成都 610500； 2.中铁西北科学研究院有限公司，甘肃 兰州 730000)

伴随着我国道路建设等工程事业的迅猛推进，硬岩(灰岩、砂岩)夹软岩(煤线、泥岩)形成的顺层滑坡严重威胁着道路的运行安全[1-2]。顺层边坡的失稳受控于软弱夹层[3]，且具有明显的渐进破坏特征，这种渐进破坏宏观上体现在边坡的变形特征[4]，细观上体现在岩土体参数的软化过程方面[5]。

Skempton[6]最早将渐进破坏的概念应用于边坡分析中，并指出边坡的失稳是由局部到整体的渐进破坏过程。目前关于边坡渐进破坏的研究方法主要有力学模型法、极限平衡法与有限差分数值模拟方法[7]。一些学者[5, 8-10]提出不同的力学模型说明了滑坡的渐进破坏过程，但这些力学模型均为理论分析，很难直观地表现渐进破坏的过程以及软化过程中岩土体参数变化的时效性与空间性，效果并不令人满意。

部分学者[11-13]考虑了岩土体的应变软化性质，以极限平衡法来研究滑坡的渐进破坏，但这些方法将岩土体的强度参数视为一次性跌落的软化材料，未能充分考虑应变软化的过程[14]。为了解决强度参数被视为一次性跌落这方面的不足，张嘎[14]和王振等[15]基于不同的条分法思想，所提出的边坡稳定性计算方法可兼顾土体受剪过程中其抗剪能力与剪应变之间的量化关系。

相比于力学模型法与极限平衡法很难直观地表现滑坡的渐进破坏过程，数值模拟方法能够克服这样的缺点。余飞等[16]较早地采用数值模拟的手段，得到了边坡临滑状态下的位移场、应力应变场等变化规律，说明了顺层岩质边坡的破坏是一个渐进破坏的过程。何忠明等[17]基于应变软化模型采用有限差分数值模拟技术，研究了软岩高边坡开挖过程中的变形与塑性区分布规律。虽然基于应变软化的有限差分方法可以直观展现边坡渐进破坏的过程，但很难求解滑坡的安全系数。为了克服这个缺点，陈国庆等[18-19]和王伟等[20]采用动态强度折减法，得到了不同计算时步下边坡的安全系数与塑性区变化图，真实再现了边坡渐进破坏的过程，但对于折减方式的确定仍然需要进一步的研究。沈华章[21]、薛海斌[22-23]和邓琴等[24]采用应变软化边坡的矢量和分析法，分析了均质边坡的渐进破坏过程，并揭示了随着计算时步增加，安全系数逐渐减小的客观规律。此种方法将数值模拟与矢量和法相结合，为边坡安全系数的求解开拓了新的研究思路。

总结前人所作的研究，发现当下对含软弱夹层的顺层岩质边坡渐进破坏的研究主要存在以下几点不足：1)虽然极限平衡法在获取安全系数上相对有优势，但目前大多数学者在采用极限平衡法时，都将岩土体的强度参数考虑为一次性跌落的材料，忽略了岩土体的软化过程分析[14]。2)有限差分数值模拟能够直观地表现滑坡的渐进破坏，但较难获得应变软化状态下的安全系数[25]；3)基于应变软化本构模型的研究对象为均质滑坡，而对基于同种模型的顺层岩质滑坡的研究文献相对较少。4)滑坡渐进破坏实质上是软弱夹层力学参数逐渐减弱的过程[5]，而当前学界对这一点的认识还不够充分，对夹层的应变软化及其蠕变特性还缺少研究。本文针对软弱夹层的应变软化的特点，采用应变软化本构模型，将极限平衡法与有限差分数值模拟方法各自的优点相结合，提出了有限差分极限平衡法，并以典型算例求解不同时步下边坡的安全系数；此外本文基于受推力状态下滑坡的应变软化过程，研究推重比(所受推力与滑体自重的比值)大小对滑坡渐进破坏的影响机理以及滑坡渐进破坏过程中强度参数的时效性与空间性，直观地表现了滑坡在渐进破坏过程中的失稳规律。

1 有限差分极限平衡法的实现

1.1 应变软化本构

应变软化的定义是由Terzaghi等[26]率先给出的，揭示了当岩土体受应力作用超过极限强度后，其本身的强度值随变形的进一步发展而逐渐减小至残余值的客观规律。本文采用FLAC3D软件内置的应变软化模型[27]，其核心是建立软化参数和Mohr-Coulomb屈服准则间的数学联系，借此展现材料(软弱夹层)的强度参数在渐进屈服过程中的软化特征。塑性剪应变Kps是关键软化参数，其增量表达式如下：

(1)

分析应变软化本构模型，为了便于后续分析计算，可将材料(软弱夹层)的强度参数弱化过程简单视作两段线型函数关系[21]，见图1，表示为式(2)：

图1 软弱夹层的强度参数软化规律Fig.1 Softening law of strength parameters of weak interlayer

(2)

式中：ω代表内摩擦角φ及粘聚力c；p代表其强度参数峰值，r代表其残余值；γ代表塑性等效应变；γ*代表残余状态对应的软化参数阈值。

式(2)是对强度参数(包括粘聚力和内摩擦角)的统一表述，表明两种强度参数将被视作进行同步弱化，这是一种简化的结果，但可以基本反映滑带强度参数的应变软化关系，检验方法可参照文献[28]进行实验验证。本文以等效塑性应变γ作为软化参数，基于Mohr-Coulomb准则进行研究，为了便于计算和带入参数，可从公式(2)分别得到粘聚力c及内摩擦角φ与等效塑性应变γ的函数关系，如式(3)、(4)：

(3)

(4)

式中，cp、φp代表峰值处的粘聚力、内摩擦角；γr、cr、φr代表残余处的等效塑性应变、粘聚力、内摩擦角；取值大小可见表1。

能够体现应变软化的Mohr-Coulomb屈服准则的数学表达如式(5)：

(5)

式中：σ1和σ3分别代表大主应力与小主应力；拉应力为正向，压应力为负向；c与φ各自代表粘聚力与内摩擦角，均是软化参数γ的函数。

1.2 安全系数定义

安全系数Fs的定义可根据极限平衡法给出：

(6)

其中F为抗滑力，F′为下滑力。

滑体的总长度为L，滑体总重为W，滑动方向受到的力为T，滑动面倾角为α。由于软弱夹层具有应变软化的性质，滑带土在不同位置的抗剪强度不同，考虑滑带土的空间变异性与时效性，将滑体分为如图2所示的n个相等的条块，每个条块的长度为l，每个条块的自重为w。整个滑体所受的抗滑力可以根据摩尔-库伦准则给出：

(7)

其中φi、ci为第i个条块的抗剪强度参数。

整个滑体的下滑力F′为：

F′=Wsinα+T.

(8)

将式(6)、(7)和(8)联立，可得安全系数：

(9)

1.3 计算步骤

将极限平衡法和有限差分数值模拟相结合，提出了有限差分极限平衡法，该方法具体实现过程见图3。

(1)对整个滑坡赋予摩尔-库伦本构模型，获取滑坡模型的初始地应力。

(2)对滑带(软弱夹层)采用应变软化本构模型，而为滑床与滑体等部分赋予摩尔-库伦本构模型，并计算平衡。

(3)通过有限差分软件显示滑带强度参数，获取滑坡软化后的粘聚力和内摩擦角。

(4)将软化后的强度参数代入到极限平衡方程中，求解安全系数。

2 算例分析

2.1 计算模型

建立一个滑坡模型，使其上下边界的垂向高度60 m，左右边界水平距离100 m。其中滑体长度为60 m，厚度5 m，软弱夹层(滑带)厚度0.5 m。滑床坡脚距模型的顶部边界垂向高度40 m，距底部边界垂向高度20 m，距左边界水平距离20 m。滑床坡顶距模型右边界水平距离同为20 m。模型网格划分见图4，共计18 400个单元，21 307个节点。且对其左右边界赋予法向约束条件，为模型底部边界赋予全约束条件。

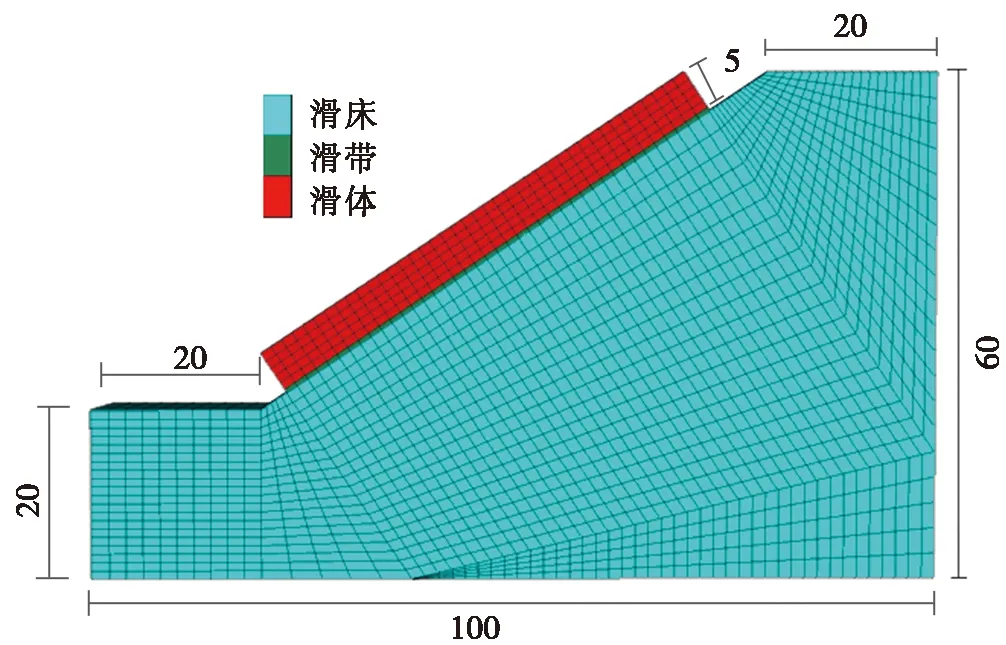
图4 模型尺寸与网格划分(单位：m)Fig.4 Model size and mesh generation

2.2 计算参数

计算过程中为软弱夹层(滑带)赋予应变软化Mohr-Coulom模型，而为滑床和滑体等部分赋予摩尔-库伦本构模型，并以材料的峰值强度作为该模型的计算参数，具体参数取值如表1。需要说明的是，自然界中的多数边坡均是长期存在的，故而在实际计算中未考虑峰值强度之前的力学参数，而重点关注软化过程中安全系数的计算。

表1 岩土体强度参数Table1 Strength parameters of rock and soil

2.3 对比多种方法求解安全系数

(1)按本文上节求解安全系数的思路，对模型不施加任何外力，通过软件计算边坡在不同时步下的抗剪强度参数如图5。求出时步1 000～10 000之间的安全系数为1.46。由式(9)不难看出，此种方法求得安全系数的精度与图2中条块的划分数量有关，而条块划分数量在实际的计算中体现为对滑带抗剪强度参数软化过程模拟的“细密程度”上，本文在兼顾结果合理性和计算便捷性的基础上，将滑带抗剪强度的弱化体现为5个“等级”，各相邻等级的的粘聚力相差100 Pa，内摩擦角相差0.1°。而事实上，在不考虑计算能力的基础上，可以通过FLAC3D软件细化两个相邻“等级”间的强度差异，即对应增多“等级”数量，在安全系数的计算过程中则表现为增多条块划分数量，能够使得所求解的安全系数更加精确。

图5 Step5000滑带强度参数图Fig.5 Strength parameter diagram of sliding belt at step 5000

对于具有应变软化性质的边坡，其安全系数应在峰值安全系数与残余安全系数之间[14, 21, 29, 30]，为说明该方法的有效性，分别采用了极限平衡法中的Bishop法和Spencer法以及强度折减法(SRM)计算该边坡在峰值强度与残余强度下的安全系数。

(2)强度折减法

以强度折减法来计算边坡稳定性，本质上是通过对岩土体抗剪参数的不断折减来实现的。每一轮折减将获得一组新的强度参数，便以该组参数进行稳定性计算，这一过程中逐渐增大折减系数，如此循环直至达到边坡的极限平衡状态，此刻折减系数即为边坡安全系数，定义如下：

(10)

Φ′=arctan(tanΦ/Fs).

(11)

式中，c、Φ各自代表岩土体折减前的粘聚力、内摩擦角；c′、Φ′ 各自代表岩土体折减后的粘聚力、内摩擦角；

Fs代表折减系数。

岩土体强度参数折减过程中任意一点的应力状态能以摩尔应力圆来表现，如图6，代表岩土体未发生破坏时的实际强度，随即增大折减系数Fs，则A—A线逐渐靠近摩尔圆，直至与摩尔圆相切时(C—C)，象征岩土体达到极限平衡状态，以此刻折减系数作为安全系数。本文使用FLAC3D软件内置模块对算例峰值、残余强度下的安全系数进行求解，分别为1.41和0.96。

图6 强度折减法示意图Fig.6 Schematic diagram of strength reduction method

(3)极限平衡法种类较多，常用的有Janbu法、Bishop法、Spencer法等。每种方法都对条块受力提出了不同的假设条件，为了验证本文所提出的有限差分极限平衡法计算结果的合理性，采用边坡稳定性分析软件，以Bishop法和Spencer法分别对算例峰值和残余两种状态下的安全系数进行求解。

Bishop法、Spencer法所求的安全系数接近，如图7，峰值强度时安全系数分别为1.48和1.485，而残余状态下分别为1.005和1.010。将本节所采用的强度折减法(SRM)、Bishop法、Spencer法和有限差分极限平衡法这四种方法的计算结果相对比，如表2。

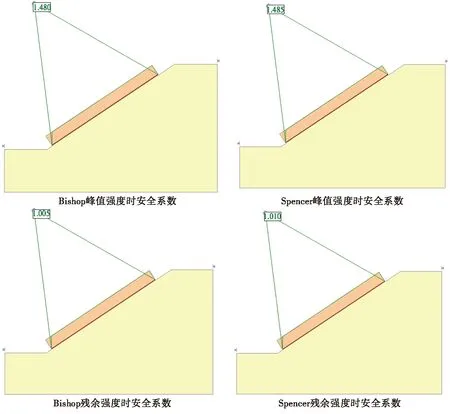
图7 极限平衡法求解安全系数Fig.7 Graphics for solving safety factor by limit equilibrium method

表2 各种计算方法结果Table2 Results of various calculation methods

从结果来看，采用有限差分极限平衡法算得安全系数为1.46，略小于2种极限平衡法在峰值强度下的计算结果，而比强度折减法在峰值强度下的安全系数1.41略大。要知道，有限差分极限平衡法会对滑带考虑应变软化效应，而该法实际上又脱胎于极限平衡法，理论上只要边坡存在应变软化效应，则该法求得的安全系数就应该小于极限平衡法在峰值强度下的计算结果。显然，文中边坡受自重影响，在坡脚形成了应变软化(图5)，虽然边坡位移较小，并未发生破坏，但求解的安全系数小于极限平衡法的峰值结果是合理的。另一方面，强度折减法求解安全系数对网格划分具有依赖性[23]，故而计算结果受网格划分方式影响较大，使得本文方法所求解的安全系数略大于强度折减法的峰值结果。此外，有限差分极限平衡法的计算结果，远大于其它3种方法在残余状态下算得的安全系数，说明对本文模型采用残余值进行计算的确过于保守。基于以上分析可知，此时边坡稳定，应变软化并不明显，故而安全系数接近于其它方法在峰值强度下的安全系数。通过与强度折减法(SRM)和极限平衡法(Bishop法、Spencer法)的计算结果进行对比分析，说明采用有限差分极限平衡法求解安全系数具有一定可靠性。

3 顺层岩质滑坡渐进破坏分析

3.1 不同推重比对渐进破坏的影响

为了更清晰地认识顺层滑坡的渐进破坏方式，本文选用受推力状态下的顺层岩质滑坡作为主要研究对象。在滑体的后部施加平行于滑动方向的推力T，见图8，计算不同的推重比T/M下安全系数随时步的变化过程，结果见图9。

须知滑体模型长度为60 m，厚度5 m，计算模型的宽度为1 m，滑体重度23 kN·m-3，故滑体自重M=6.9×103kN。故而当滑体受平行于滑动方向的应力分别为150 kPa/200 kPa/250 kPa/300 kPa/350 kPa/400 kPa时，对应推重比T/M=0.109/0.145/0.181/0.217/0.254/0.290。安全系数随计算时步的变化过程由图9可见，当顺层岩质边坡推重比T/M≦0.145时，边坡的安全系数几乎不变，后缘推力不足以使滑带发生应变软化，所以宏观上体现安全系数没变化，边坡一直处于稳定的状态。随着推重比增大，伴随计算时步增加，边坡安全系数不断减小。当T/M=0.181时，安全系数自3 000步开始降低，5 000步时安全系数骤降，8 000步时彻底失稳；T/M=0.290时，安全系数自1 000步开始降低，2 000步安全系数骤降，4 000步彻底失稳。即推重比越大，安全系数减小越快，软弱夹层软化的越快。

3.2 软弱夹层强度参数演化与特征点变化规律

以推重比T/M=0.181为例，分析滑带在整个渐进破坏的过程中，其软弱夹层强度参数的空间变异性以及时效性的变化规律，并监测滑带上6个监测点(图8)的强度参数变化情况，数值模拟结果见图10和图11。

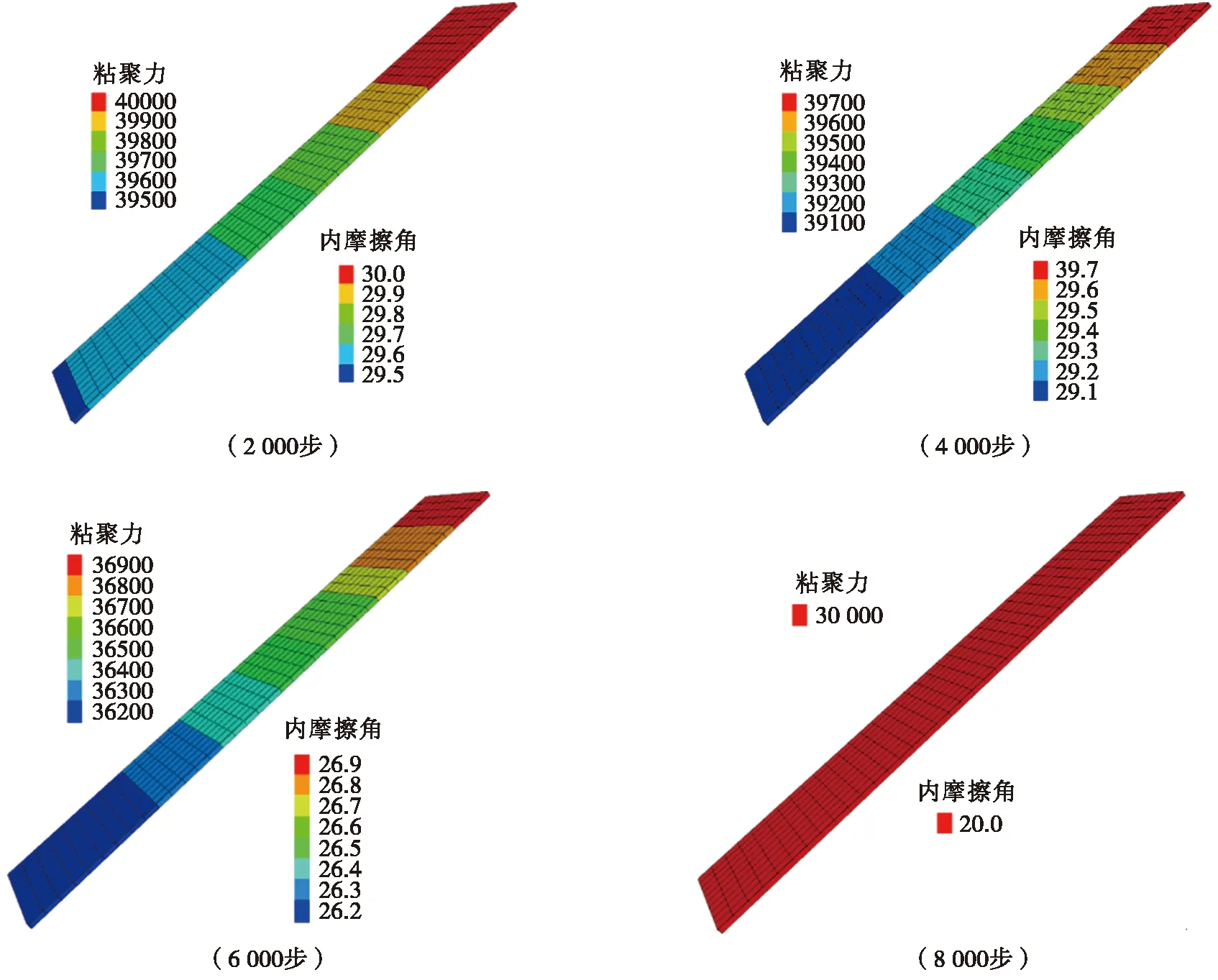
图10 不同时步下强度参数云图Fig.10 Strength parameter nephogram at different computing steps

由图10可知，坡脚处的强度参数始终小于坡顶处，证明滑坡首先从坡脚处开始软化，并向坡顶处逐渐发展。从图11来看，3 000时步之前，6个监测点的强度参数软化速度较慢，其中监测点6的强度参数未见明显变化，而其余5个监测点的强度参数可见软化现象，以监测点1最为明显，也证实滑坡先从坡脚处软化，并向坡顶处逐渐发展的论断。3 000时步之后，随着时间步的增大，强度参数明显减小；且在4 000时步之后，强度参数开始骤减，宏观上表现为安全系数突然减小(见图9)，且6个监测点强度参数逐渐接近，说明整个滑带应变软化充分发育，在8 000时步时，6个监测点强度参数同时达到残余强度，整个软弱夹层完全软化，此时滑坡已彻底失稳。

3.3 滑带位移变化特征与滑坡渐进破坏分析

为分析边坡渐进破坏过程中滑带位移变化的规律，在滑带中设置如图6所示的6个特征点，监测其位移量的变化，监测结果见图12。

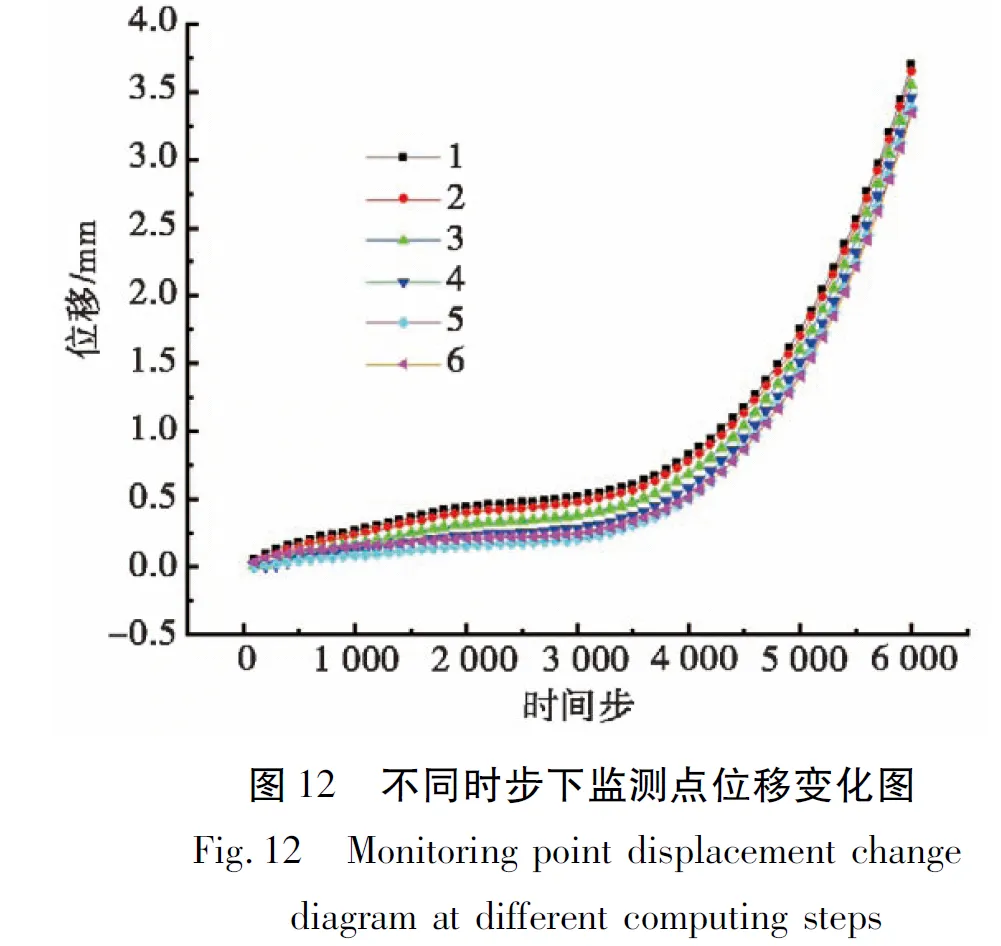
由图12 可见，当边坡推重比T/M=0.181时，在0～3 000时步范围内，6个特征点的位移量增加极为缓慢，最大位移出现在坡脚，小于0.5 mm。结合图11可知，这一阶段滑带坡顶处的强度参数仍然处于峰值强度，而其他部分出现微弱软化现象，而据图9，该阶段边坡安全系数保持在1.37左右无明显变化；在3 000～6 000时步范围内，可见所有特征点位移量呈现加速增大趋势，且坡顶、坡脚处的位移量开始接近。从图9、图11可知，这一阶段滑带强度参数软化过程提速，安全系数加速锐减至1.22；6 000～8 000时步，滑带强度参数保持最大的软化速率，近乎匀速跌至残余强度，于此同时安全系数以最大速率同步跌破1.0；8 000时步之后，边坡早已彻底失稳。参照结合郑颖人等[31]的研究成果对本算例进行变形阶段划分，在0～3 000时步，滑带上产生局部蠕动变形，可划定为蠕动阶段；3 000～6 000时步是滑带应变软化的集中发育期，该阶段滑面开始逐渐形成，可划定为挤压阶段；6 000～8 000时步，滑面贯通，可划定为滑动阶段；8 000时步之后，强度彻底丧失，滑坡高速滑动，划定为剧滑阶段。

值得说明的是，在0～4 000时步之间，6号特征点的位移值略大于5号特征点，从空间关系来看，与本文 “滑坡先从坡脚处软化破坏，并向坡顶处逐渐发展”的整体现象不符。这是因为此时该模型受到了推力作用(推重比T/M=0.181)，6号特征点最接近模型受力面，该处土体受力产生局部变形，而5号特征点离受力面相对较远，受该变形的影响较小，因此会在蠕动挤压阶段出现这种细微 “反常”。此外还需注意， 6 000时步处于挤压阶段和滑动阶段的临界点，此刻安全系数为1.22，整个滑带的强度参数都出现不同程度的软化，但尚且没有达到残余状态，此时边坡仍然稳定。然而，滑体持续受到后缘推力作用，据图12所示，6 000时步滑带上特征点的位移量有明显增大，从模拟结果来看，在持续的受力过程中，该边坡终将走向失稳。因此，这种滑带上虽然产生一定程度的位移突变，但边坡仍然基本稳定的特殊状态，为顺层岩质边坡的监测预警提供了可能。在进行顺层岩质边坡失稳监测时，应针对滑带进行监测，当监测点的位移明显增大时，说明边坡即将失稳，此时需要尽可能采取措施进行加固治理。如果能够得到妥善治理，处于挤压阶段的滑坡未必会发展到滑动阶段，可见挤压阶段是滑坡发现、预防和治理的良好时机。

4 讨论

采用极限平衡法计算顺层岩质滑坡的安全系数相比于计算均质滑坡安全系数具有更好的适用性。一方面，顺层岩质边坡的失稳可看作滑体整体移动，即满足极限平衡法将条块视为刚体的假定；另一方面，顺层岩质边坡沿着软弱夹层滑动，即滑动方向是固定的，这样可忽略条块内部的相互作用力。有限差分法相比于极限平衡法，能够克服极限平衡法将岩土体软化视为一次性跌落的缺点，此外，有限差分法能够直观地表现软弱夹层的力学参数的空间变异性和时效性，适用于模拟边坡的渐进破坏过程。将极限平衡法和有限差分法的优点相互结合，提出了有限差分极限平衡法。

本文通过具体的算例说明有限差分极限平衡法的有限性，为求解滑坡的安全系数提供了新的思路，但这仅仅是初步的探索，还有许多方面有待以后的进一步研究。例如，在有限差分极限平衡法提出的过程中，将滑带强度参数的峰后软化过程用简单的二段线型函数关系来展示，默认了c、φ进行同步软化，这固然在保证一定精度的基础上极大地简化了计算难度，但与真实的软化过程还存在一定的差距。同样的，合理确定残余软化参数在这一过程中极为重要，这对力学试验也有较高要求。此外，该方法还存在一些其他缺陷，例如当软弱夹层较厚时，在不同位置的滑体滑动方向会不相同，此时计算的安全系数会有偏差。由于篇幅所限，文中并未就这些问题展开论述。

5 结论

(1)考虑了顺层岩质边坡在渐进破坏过程中其软弱夹层的应变软化效应，将有限差分数值模拟与极限平衡法各自的优点进行有效结合，实现了有限差分极限平衡法，并以典型算例验证了此法的有效性。

(2)利用有限差分极限平衡法得到了顺层岩质边坡在不同推重比T/M下的安全系数，当推重比T/M≦0.145时，后缘推力不足以使滑带发生应变软化，宏观上体现为安全系数没有变化，边坡处于稳定状态。随着推重比和计算时步的增加，边坡安全系数不断减小。当T/M=0.181时，安全系数自3 000步开始降低，5 000步时安全系数骤降，8 000步时彻底失稳；T/M=0.290时，安全系数自1 000步开始降低，2 000步安全系数骤降，4 000步彻底失稳。即推重比越大，安全系数减小越快，软弱夹层软化的越快。

(3)通过分析滑坡在受推力状态下的应变软化过程，得到了滑坡渐进破坏过程中其滑带上强度参数的软化规律和滑带特征点的位移变化规律，当滑带上的监测点位移变化明显时，滑坡应及时采取加固措施防止变形进一步发展。