并联3-UPU舰载稳定平台运动控制设计与分析

李猛，黄振峰，陈俊贤，杨壮涛，文善贤

（广西大学机械工程学院，广西 南宁 530004）

1 前言

并联机构结构紧凑简单、承载能力强、刚度大、响应速度快等特点，可满足精准定位和快速跟踪恢复的需求，在并联机床、舰载稳定器、车载稳定器等方面被广泛使用。然而并联机构作为一个多变量、多自由度、多参数强耦合、高度非线性的复杂多刚体系统，其控制策略、控制方法较为复杂，所以如何提高并联机构的轨迹精度是控制研究的急切问题。

随着技术与软件的不断成熟，对轨迹精度控制问题的分析也不断加深，因此并联机构分析设计和控制策略研究方面也产生了许多研究成果与应用。文献[6，7]提出自抗扰控制技术，并对自抗扰控制进行介绍分析；文献[5]对6-RUS舰载并联机构进行动力学和运动学分析，并分别建立了自抗扰力矩控制和自抗扰滑膜控制；文献[8]针对6-UPS/3SPS关联机构提出基于运动学和动力学混合控制策略；文献[9]介绍了基于2RPR+P并联机构的三种控制方法：（1）全位置控制方法，（2）混合力/位置控制方法，（3）全力控制方法；文献[10]设计了3RPS和3RPS-R并联机构，并针对该并联机构进行了运动学分析和操作空间分析。目前并联机构理论研究已逐步成熟，并且随着控制技术与方法的不断发展，根据不同实际的工程应用中根据具体工程的要求，有了许多不同的并联机构和控制算法以满足适应工程要求。

本文针对实际工程，基于3-UPU并联机构，并在四、五级海况下，以052D驱逐舰数学参数为参考，设计了一种前馈加反馈PID控制器，并通过matlab/simulink软件进行仿真分析，通过仿真得到并联机构在横摇、纵摇与升沉运动三个方向的稳定误差，经过仿真对比自抗扰控制器，最后可以得出所设计控制器有效的提高并联机构的控制稳定性。

2 稳定平台运动学建模

3-UPU并联机构是一种两端连接虎克铰，中间采用移动副的一种三自由度的新型机构，通过三个防扭折叠机构承受主要重力，中间移动副进行伸缩引导，具有结构刚性强，摩擦磨损少，运动精度高和使用寿命长等优点，在并联机器人，航空航天航海等领域有着广泛的应用。

2.1 数学模型分析

3-UPU并联机构稳定平台机构简图如图1所示。分别建立平台基座坐标系、平台台面固联坐标系。其中，坐标系的原点位于基座中心，坐标轴指向舰首、指向舰船右侧、垂直甲板指向下方；坐标系的原点位于平台中心，当平台平面与甲板平行时，两坐标系对应轴互相平行。伸缩杆以120°均布在基座、起降平台的周向；折叠防扭铰链点与伸缩杆间隔60°布置，同样呈120°分布在基座、上平台的周向。

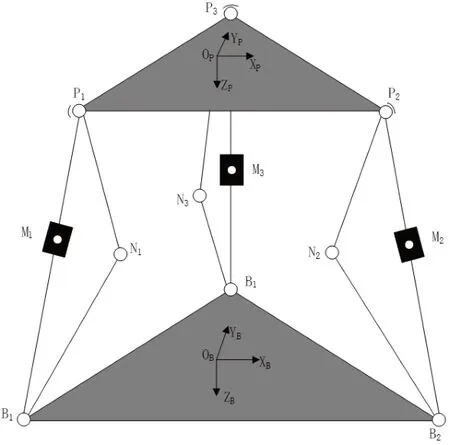
图1 平台机构示意图

用iB、iP来表示伸缩杆的下端与上端，分别对应其与基座、动平台的铰链位置， 1～3i= 对应周向角0°、120°、240°（以BBOX指向为0°，俯视时顺时针为正方向）。用h表示上台面高度，用欧拉角αβ、 表示上平台相对基座的倾斜角（旋转顺序为X-Y），则坐标系{}P与{}B之间的转换矩阵可以表示为：

其中，,YβR 表示绕Y轴旋转角度β的转换矩阵。

将 表示在坐标系{}B中，结果如下：

2.2 位置正运动学

采用析配消元法求解，以第一式为例，令：

进一步，令

可以得到关于hN的二次方程：

对式中其他方程进行类似处理，得到关于h的方程组：

任选两个方程可以得到齐次矩阵等式：

该方程有非平凡解，因此系数矩阵行列式为零，又注意到各系数受α、β影响，因此构造方程组：

其中，i,j,k∈ [1,2,3]且两两不等。求解上式即可得到α、β，反过来解得hN。通过上述方程可以求得该类型并联机构的所有解，然后根据约束条件筛选。

2.3 位置逆运动学

通过并联机构的位置关系可以得到液压缸长度变化，其数学表达为下式：

其中：

3 控制策略研究与设计

并联机构稳定平台的位置控制和速度控制模式需要机构的位置分析、速度分析和加速度分析，稳定平台控制系统中需通过传感器测量到稳定平台下平台的运动状态，也就是舰船晃动产生的干扰运动和稳定平台上平台的运动状态。控制器采集到传感器信号，根据稳定平台控制模型控制液压缸运动，实现上平台相对于惯性系的稳定。

3.1 普通控制器

（1）ADRC控制器。自抗扰控制器（ADRC）由韩京清教授提出，其由跟踪微分器（TD）、非线性误差反馈（NLSEF）、扩张状态观测器（ESO）三个部分构成，其原理结构如图2。

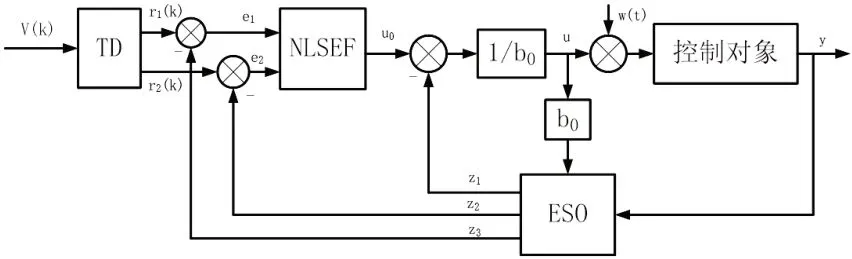
图2 ADRC控制器

为了提高控制系统的动态特性，解决系统快速响应和超调间的矛盾，运用扩张状态观测器对被控对象进行实时在线估计，利用跟踪微分器安排过渡过程，并对系统的总扰动进行补偿。

跟踪微分器。跟踪微分器属于自抗扰控制器的前馈部分，输入信号通过微分跟踪器，得到输入信号和输入微分信号。跟踪微分器可以根据输入信号的大小和控制要求来安排过渡过程，解决快速响应和超调间的矛盾，使得系统响应迅速并且没有超调。其数学表达式为：

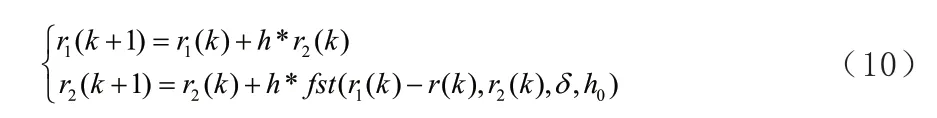
非线性状态误差反馈。由PID控制器中的控制系数线性组合会造成系统的快速响应与超调之间存在矛盾，而这种矛盾现象可以使用非线性组合可以解决，所以使用PID控制系数的非线性组合，实现自抗扰控制。其数学表达式如下：

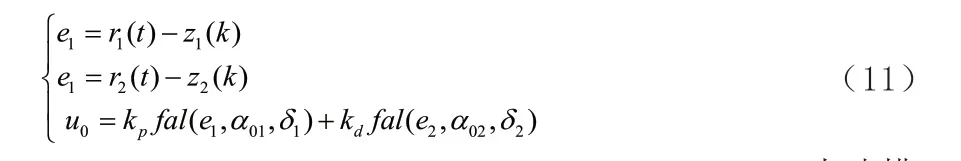
扩张状态观测器。扩张状态观测器作用是将系统未建模部分、内部参数摄动以及外界干扰等考虑为一个新的状态，给系统提供新的反馈输入信号、扩张状态变量和各阶状态变量。通过扩张状态变量估算系统的干扰，从而利用反馈来补偿系统扰动，其状态方程如下：

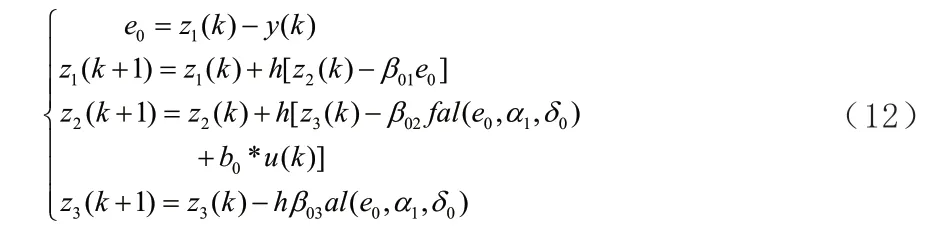
（2）前馈加反馈PID控制器。PID控制器是最早发展起来的控制策略之一，由于其算法简单、鲁棒性好并且可靠性高，所以被广泛应用于过程控制和运动控制中，在工程实践中，被控对象经过控制都能得到较好的结果。

图3 中，yd(t)是给定的理想输入信号，y(t)是经过PID控制器后的输出信号，e(t)为系统的误差信号，其值为：

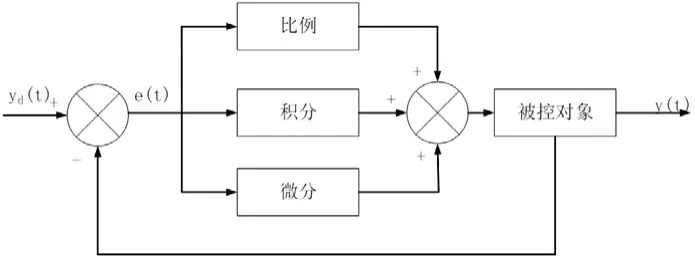
图3 PID控制器

普通PID 控制的控制规律为：

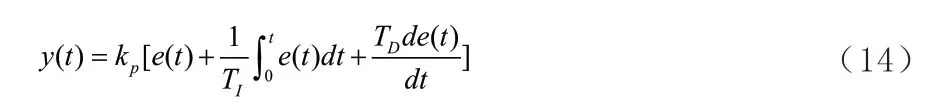
普通PID控制器，控制参数设定后，在实际工作中就很少进行调节。稳定平台属于并联机构，在结构上具有很强的耦合性，也因此会导致系统模型变化很大，普通的PID控制很难满足系统要求。通常采取的方法有自适应 、模糊和前馈，稳定平台延迟严重，为了提高系统的动态响应能力，使用前馈加反馈PID控制。其结构如图4所示。

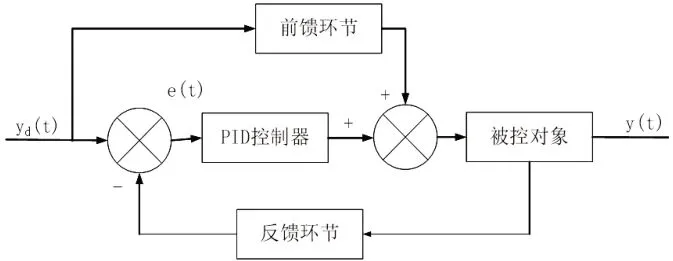
图4 前馈加反馈PID控制器

3.2 稳定平台控制器设计

并联机机构运动控制器设计过程中可分为基于运动学控制和基于动力学控制两大类，基于运动学的控制器设计主要研究并联机构的运动学关系与驱动装置的动态模型，而不用考虑并联机构的动力学模型；基于动力学控制的控制器设计则需要进行动力学分析，建立整个系统的动力学模型。

本部分主要考虑基于并联机构运动学的控制，在控制过程中主要考虑并联机构的运动规律，在控制中简化了模型的结构。其结构如图5所示。

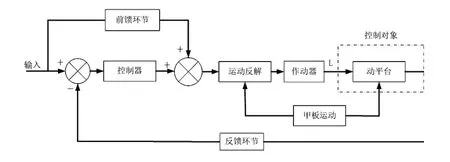
图5 基于运动的并联机构控制

并联机构作为控制结构可分为五个部分，第一部分舰船甲板的运动，这一部分主要为并联机构提供安装位置，所以这一部分的运动始终都存在整个运动控制过程；第二部分为控制器部分，该部分采用PID控制器；第三部分为运动的反解部分，在期待上平台的运动和甲板运动的共同作用下解算出作动气的运动规律；第四部分时作动气的运动，通过第二部分解算出作动气的运动规律转化为作动气的长度变化，作为液压作动器的控制规律；第五部分通过运动正解得到上平台的横摇纵摇和升沉运动，将正解得到的运动作为反馈与期待的运动作差得到控制器的控制输入。

4 不同海况下的仿真分析

4.1 仿真参数的设置

本部分仿真以052D驱逐舰参数为例：船长×船宽×船高：155m×18m×40m；排水：6300t；巡航速度：18节。不同海况的参数如表1。

表1 不同海况参数

4.2 仿真结果分析

通过仿真分析，对比图6、图7，在四级海况下，ADRC控制器横摇纵摇误差范围在±0.5°之间，升沉误差在-0.15～+0.1m之间；前馈加反馈PID控制器横摇纵摇误差在0.05°以内，升沉误差在0.01m以内。对比图8、图9，在五级海况下，ADRC控制器横摇纵摇误差范围在±0.52°之间，升沉误差在±0.15m之间；前馈加反馈PID控制器横摇纵摇误差在0.05°以内，升沉误差在0.01m以内。两种不同的海况不同控制器控制效果误差结果进行对比分析，在本应用场景中，无论在四级海况还是五级海况下前馈加反馈PID控制器都优于ADRC控制器。

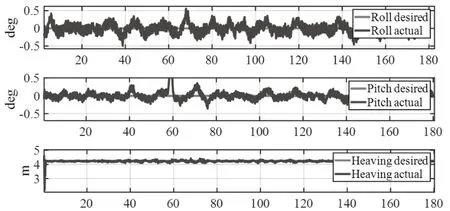
图6 四级海况下ADRC控制器误差

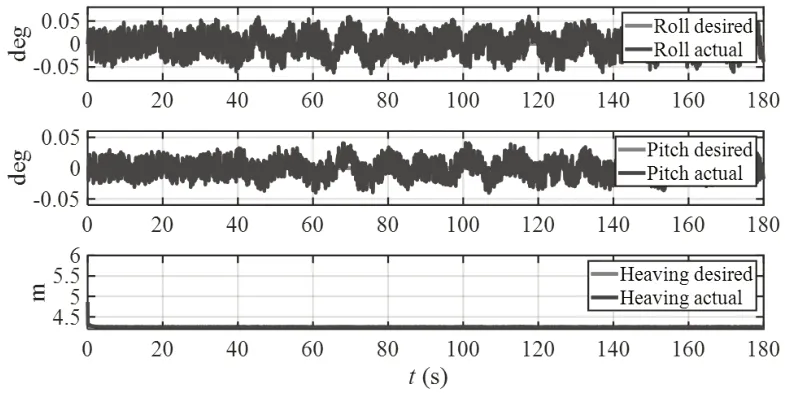
图7 四级海况下前馈加反馈PID控制器误差

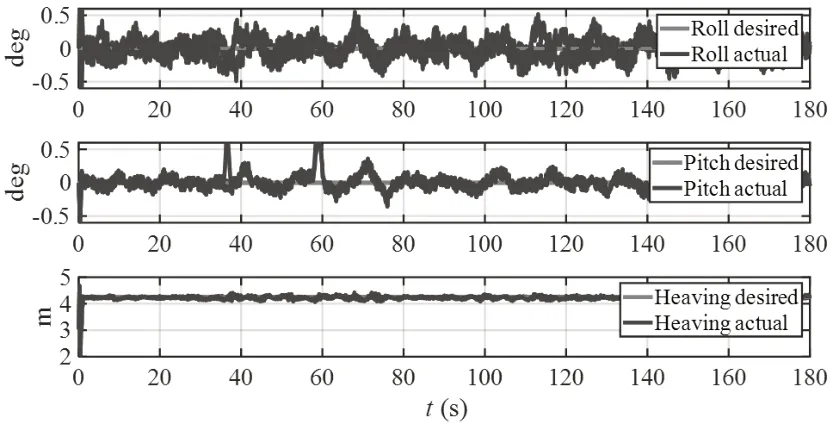
图8 五级海况下ADRC控制器误差

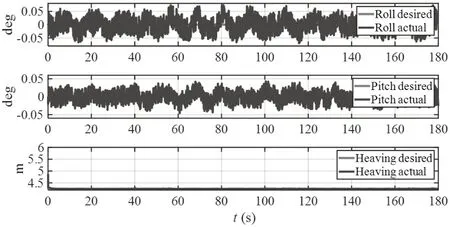
图9 五级海况下前馈加反馈PID控制器误差

5 结语

基于并联3-UPU稳定结构，并通过解析分析得到并联机构的运动学方程，得到了控制仿真的控制对象。在PID控制策略的基础上，设计一种反馈加前馈的PID控制和ADRC控制器，通过对比并联机构运动时的横摇纵摇和升沉运动三个方向的误差进行仿真分析，仿真表明：前馈加反馈PID控制能够很好的满足稳定平台的精度要求，在该场景运行下，前馈加反馈PID控制器的结果明显优于ADRC，并且该控制结构稳态误差小和鲁棒性强等优点。该设计方法和控制策略为稳定平台的研究提供了一种可行的参考方案。