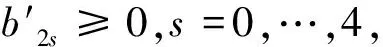直径为5的一类树的拟序
2021-12-20杜轻松贾亚荣李亚宁王志慧火博丰
杜轻松,贾亚荣,李亚宁,王志慧,火博丰,2*
(1.青海师范大学 数学与统计学院,青海 西宁 810008;2.青海省物联网重点实验室,青海 西宁 810008)
0 引言
一个图G的能量可以被定义为其邻接矩阵特征值的绝对值之和[1].研究图能量的排序有一定的化学背景.能量概念最早源于人们对共轭碳氢化合物分子的全部π-电子能量的近似估计.由分子化学理论,共轭分子的图能量越大,相对应的热力学稳定性越强.近年来,关于图能量的研究有很多结果.对于树的极值能量,上世纪70年代Gutman[2]首次得到n个顶点的具有第一、第二极大能量和第一,第二,第三、第四极小能量的树的结构,其中路Pn和星图Sn分别是最大能量和最小能量的图;2008年,李书超等[3]确定了第三大能量树的结构.2010年火博丰等[4]确定了具有第四大能量树的结构.2012年,Andriantiana[5]刻画了直径为n-i-1(其中i=1,2,3,4,6,8,10,12,14,16,18)的极大能量树的结构,对相当大的n,确定出了当n为奇数时从第1到第3n-84的极大能量树和当n为偶数时从第1到3n-87的极大能量树的结构.2005年,晏卫根[6]等人确定了给定直径的具有极小能量的树的结构.关于给定小直径的具有极大能量的树,欧建平[7]确定了中心点的度为且直径为4的具有极大能量树的结构.索南仁欠[8]等人给出了直径为3和4的具有极大能量的树的结构.乔小琴等[9]给出了直径为5的具有极大能量的树的一个必要条件.在此基础上,贾亚荣等[10]给出了直径为5的具有极大能量的树的结构范围.本文讨论当p≥q+2,q=1时,这类直径为5的树的悬挂点分配与拟序变化,进而与能量变化的关系.
1 基础知识
令G是阶为n,邻接矩阵为A(G)的图,并且令G的特征多项式为φ(G,x)或φ(G).
图G的特征多项式与它的结构的关系可以由下面的sachs引理来体现.
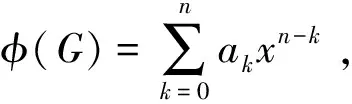
Lk表示图G有k个顶点的Sachs子图的集合,即子图的每个分支要么是k2,要么是圈;ω(S)与c(S)分别表示在S中的连通分支个数和包含圈的个数.此外,a0=1.
从Sachs引理容易看出,如果图G是一个二部图,那么对于任意k≥0,a2k+1=0.因此
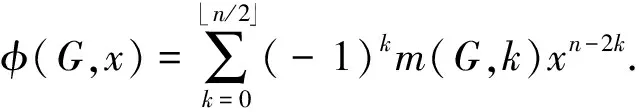
对于图G的特征多项式,有如下的递推公式.
引理1.2[1]令uv是图G的一条边,则
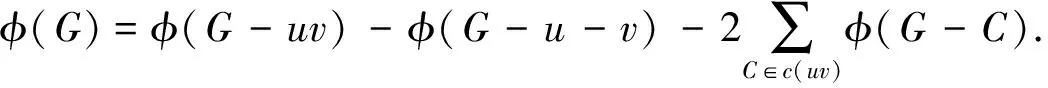
c(uv)表示包含uv的圈集.特别的,如果uv表示悬挂边,v表示悬挂点,则
φ(G)=xφ(G-uv)-φ(G-u-v).
从引理1.2明显看出G是无圈图时的递推公式如下.
推论1.1[2]图G是一个森林且图G的一条边e=uv,则图G的特征多项式为,
φ(G)=φ(G-e)-φ(G-u-v).
关于图G的能量有如下定义.
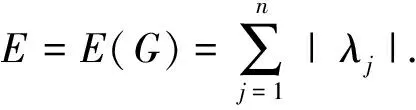
1940年,Coulson[11]获得了经典的Coulson积分公式,它把离散的特征值与如下的连续函数的积分联系起来:
当G1和G2是两个有相同点顶点的图,则可直接应用得到如下公式:
对于n个顶点图G的能量,也可表示为
(1)
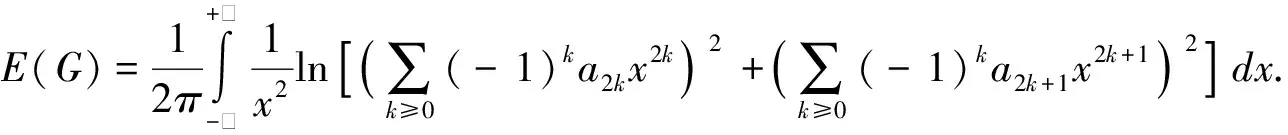

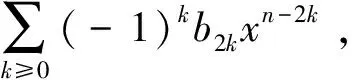
(2)

从(2)以及对数函数和积分的性质,他们观察到拟序和能量大小存在如下关系:
G1≼G2⟹E(G1)≤E(G2),
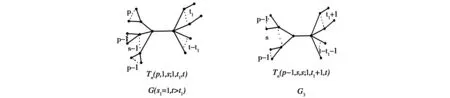
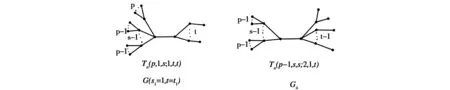
G1G2⟹E(G1) 这个关系是能量研究的一个重要工具. 乔小琴[9]等首先定义了如下的一类树:(1)固定两个中心点的度分别为s+1和t+1;(2)对度分别为s+1和t+1的两个中心点,到每个中心点的距离为2的悬挂点的个数分别固定为a和b.记这样一个树的集合为Tn(a,s;b,t),注意到a+b=n-s-t-2.这相当于给直径为5的n阶树做了一个划分{Tn(a,s;b,t)|s,t≥1;a,b≥1}.他们发现在每个图类Tn(a,s;b,t)中,每一侧的悬挂点分配越均匀,拟序越大.且在每一类图中具有极大拟序的图唯一确定,记为T(p,s1,s;q,t1,t)(如图1),它除了满足图类Tn(a,s;b,t)的条件(1),(2)之外,还要满足条件(3):对于与同一中心点相邻的任意两个(非中心)点,与它们分别相邻的悬挂点的个数之差不超过1.这里a=(p-1)s+s1,1≤s1≤s,b=(q-1)t+t1,1≤t1≤t.注意到p和s1被a,s唯一确定,q和t1被b,t唯一确定.因此我们可以把Tn(p,s1,s;q,t1,t)简写为Ta,s;b,t. 图1 引理1.3[9]对任意T∈Tn(a,s;b,t),有TTn(p,s1,s;q,t1,t)=Ta,s;b,t. 引理1.4[10]对图Tn(p,s1,s;q,t1,t)=G,若p≥q+2,q≥2. (1)当s1>1,t>t1时,Tn(p,s1-1,s;q,t1+1,t)≻G; (2)当s1>1,t=t1时,Tn(p,s1-1,s;q+1,1,t)≻G; (3)当s1=1,t>t1时,Tn(p-1,s,s;q,t1+1,t)≻G; (4)当s1=1,t=t1时,Tn(p-1,s,s;q+1,1,t)≻G. 对于p≥3,q=p-1时的情形,贾亚荣等[10]得到类似结论. 引理1.5[10]令G=Tn(p,s1,s;p-1,t1,t),t>t1≥1,s>s1≥1,p≥3. (1)若s1>1,则GTn(p,s1-1,s;p-1,t1+1,t); (2)若s1=1,则GTn(p-1,s,s;p-1,t1+1,t). 定理设T(p,s1,s;q,t1,t)=G,若p≥q+2,且q=1,s≥s1≥1,t≥t1≥1. (1)当s1>1,t>t1时,Tn(p,s1-1,s;1,t1+1,t)≻G; (2)当s1>1,t=t1时,Tn(p,s1-1,s;2,1,t)≻G; (3)当s1=1,t>t1时,Tn(p-1,s,s;1,t1+1,t)≻G; (4)当s1=1,t=t1时,Tn(p-1,s,s;2,1,t)≻G. 证明:(1)设Tn(p,s1,s;1,t1,t)=G,Tn(p,s1-1,s;1,t1+1,t)=G1;如图2所示. 图2 根据推论1.1的特征多项式的递归公式,可以将G和G1的特征多项式按如下方式化简: φ(G)=φ(T(p,s1,s))φ(T(1,t1,t))-φ(Sp+1)s1φ(Sp)s-s1φ(S2)t1φ(S1)t-t1 =xt-t1-1φ(K2)φ(Sp+1)s1-1φ(Sp)s-s1-1{x2p-2[x4-(2p+s-1)x2+(p2+sp-p-s1)] φ(G1)=φ(T(p,s1-1,s))φ(T(1,t1+1,t))-φ(Sp+1)s1-1φ(Sp)s-s1+1φ(S2)t1+1φ(S1)t-t1-1 =xt-t1-2φ(K2)t1φ(Sp+1)s1-2φ(Sp)s-s1{x2p-2·[x4-(2p+s-1)x2+(p2+sp-p-s1+1)] 令H(x)=φ(Sp+1)s1-2φ(Sp)s-s1-1φ(K2)t1-1φ(S1)t-t1-2 f1(x)=x4-(2p+s-1)x2+(p2+sp-p-s1) f2(x)=x4-(1+t)x2+(t-t1) g1(x)=f1(x)+1 g2(x)=f2(x)-1 h(x)=(p-1)·(x2-p)·(x2-(p-1))(x2-1) 则 φ(G1)-φ(G)=xt-t1-2φ(K2)t1-1φ(Sp+1)s1-2φ(Sp)s-s1-1{φ(K2)φ(Sp)[x2p-2·[x4-(2p+s-1)x2 +(p2+sp-p-s1)][x4-(1+t)x2+(t-t1)]-(p-1)(x2-p)(x2-(p-1)) (x2-1)]-xφ(Sp+1)[x2p-2·[x4-(2p+s-1)x2+(p2+sp-p-s1)] [x4-(1+t)x2+(t-t1)]-(p-1)(x2-p)(x2-(p-1))(x2-1)]} 因为s1>1,t>t1,则: b'0=p-1>0. b'2=p(2p-3)+s(p-2)+tp+1>0. b'4=(p-2)(p2+sp-p-s1)+(p-1)(4p+2tp+st+t-t1)+t>0. b'6=(p-1)((2p+s)(t-t1)+(2p2+1+t1-2p+sp-s)+p(t-t1-1)>0. b'8=(p-1)(p2+sp-p-s1)(t-t1)+(p-1)(t-t1-1)+p(p-1)2>0. 当k=0,1时,(-1)k(b2k(G1)-b2k(G))=0. (2)设Tn(p,s1,s;1,t,t)=G,Tn(p,s1-1,s;2,1,t)=G2;如图3所示.与(1)类似可得 图3 φ(G)=φ(T(p,s1,s))φ(T(1,t,t))-φ(Sp+1)s1φ(Sp)s-s1φ(K2)t φ(G2)=φ(T(p,s1-1,s))φ(T(2,1,t))-φ(Sp+1)s1-1φ(Sp)s-s1+1φ(S3)φ(S2)t-1 =φ(Sp+1)s1-2φ(Sp)s-s1φ(K2)t-2{x2p[x4-(2p+s-1)x2+(p2+sp-p-s1+1)] 令H(x)=φ(Sp+1)s1-2φ(Sp)s-s1-1φ(S2)t-2 f1(x)=x4-(2p+s-1)x2+(p2+sp-p-s1) f2(x)=x2-(1+t) g1(x)=x4-(2p+s-1)x2+(p2+sp-p-s1+1) g2(x)=x6-(3+t)x4+(1+2t)x2 h(x)=(p-2)(x2-p)·(x2-(p-1))(x2-1) 则 因为s1>1,t=t1,则 b'0=1-1=0.b'2=-3-t-p+3+p+t=0. b'4=p-1>0.b'6=(2p+s-1)(p-3)+tp-t+2p-1>0. b'8=(p-1)(p2+sp-p-s1+t)+(1+2t)+(tp-2t-1)(2p+s-1)+2p(p-2)>0. b'10=(tp-2t-1)(p2+sp-p-s1)+(p-1)(1+2t)+(p-2)(p2+p-1)>0. b'12=p(p-1)(p-2)>0. (3)设Tn(p,1,s;1,t1,t)=G,Tn(p-1,s,s;1,t1+1,t)=G3;如图4所示: 图4 φ(G)=φ(T(p,s1,s))φ(T(1,t,t))-φ(Sp+1)φ(Sp)s-1φ(S2)t1φ(S1)t-t1 =xt-t1-1φ(Sp)s-2φ(K2)t1-1{x2p-2[x4-(2p+s-1)x2+(p2+sp-p-1)]·[x4-(1+t)x2 φ(G3)=φ(T(p-1,s,s))φ(T(1,t1+1,t))-φ(Sp)sφ(S2)t1+1φ(S1)t-t1-1 =xt-t1-2φ(SP)s-1φ(K2)t1{xp-1[x2-(p+s-1)][x4-(1+t)x2+(t-t1-1)x2]-xφ(K2)φ(SP)} 令H(x)=φ(Sp)s-2φ(S2)t1-1φ(S1)t-t1-2 f1(x)=x4-(2p+s-1)x2+(p2+sp-p-1) f2(x)=x4-(1+t)x2+(t-t1) g1(x)=x2-(p+s-1) g2(x)=x4-(1+t)x2+(t-t1-1)x2 h(x)=(p-1)(x2-(p-1))(x2-1) 则 因为s1=1,t>t1,则 b'0=1-1=0.b'2=0.b'4=p-1>0. b'6=(2p+s-2)(t-t1)+(p-1)(p+s+t+1)-(2p+s)+(1+t)>0. b'8=8t-3t1+2st-s-1>0. b'10=(p-1)(p+s-1)(t-t1-1)+(p-1)2>0. (4)设Tn(p,1,s;1,t,t)=G,Tn(p-1,s,s;2,1,t)=G4.如图5所示: 图5 φ(G)=φ(T(p,1,s))φ(T(1,t,t))-φ(Sp+1)φ(Sp)s-1φ(S2)t =φ(Sp)s-2φ(K2)t-1{x2p-1[x4-(2p+s-1)x2+(p2+sp-p-1)][x2-(1+t)] φ(G4)=φ(T(p-1,s,s))φ(T(2,1,t))-φ(Sp)sφ(S3)φ(S2)t-1 令H(x)=φ(Sp)s-2φ(K2)t-2 f1(x)=x4-(2p+s-1)x2+(p2+sp-p-1) f2(x)=x2-(1+t) g1(x)=x2-(p+s-1) g2(x)=x6-(3+t)x4+(1+2t)x2 h(x)=(p-2)(x2-(p-1))(x2-1) 因为s1=1,t=t1,则 b'0=1-1=0.b'2=0. b'4=p-2>0.b'6=p2-3p+tp-t+sp-3s+2>0. b'8=p(p-3)(t+1)+s(t(p-2)-1)+t+2>0. b'10=(p-2)(p-1)>0.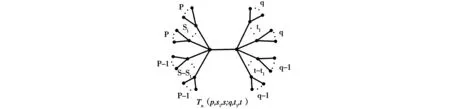
2 主要定理