基于自适应新息卡尔曼滤波的脱靶量预测算法*

杨丽君，刘 博，王 军，陈天群，雷俊杰

(1.南京理工大学自动化学院，江苏 南京 210094；2.上海机电研究所，上海 201109)

脱靶量是始点在目标上，终点在弹头上的一个矢量。脱靶量的精确预测是实现后续闭环校射的基础。所以，为完成真正意义上的火控系统闭环控制，需要提高脱靶量预测的精度。

建立脱靶量预测模型，首先需要对射击误差的特性规律进行分类与分析。查阅国内外学者关于误差源的分析研究可知，脱靶量可以分为确定性误差分量和随机误差分量。确定性误差通常也称为系统误差，在工程应用中一般以常量代替；随机误差分量可依据时间相关性将其分为可修正误差和不可修正误差。综合考虑误差源特性后，叠加生成误差序列。

预测弹丸与已发弹丸之间的相关性是建立各阶次预测模型的基础。目前，广泛使用的脱靶量预测模型大多仅考虑只有前后两发弹之间存在相关性的一阶模型[1-3]，但是，随着火炮射速的不断提高，尤其是在射频很高的情况下，一阶误差模型的假定误差较大，与实际不符。因此，本文对高阶模型进行相关研究。

传统卡尔曼滤波算法是基于最小方差估计的递推式滤波方法，在动态系统的估计、预测和控制中使用广泛[4]。在系统状态已知，过程噪声和测量噪声的统计特性精确的情况下，传统卡尔曼滤波算法能够实现最优估计。但是，实际应用中的系统状态大都是先验未知，而且预测模型单一造成预测的精度较低、稳定性较差，甚至造成滤波发散。目前，国内外学者提出了一系列基于传统卡尔曼滤波的改进算法来解决这些问题，从而提高卡尔曼滤波的精度和普适性。

文献[5]提出了一种Sage-Husa 自适应滤波算法，该算法通过协方差匹配技术实现在线估计噪声统计特性；文献[6]提出了一种通过任意时刻施行 2 次传统卡尔曼滤波算法的方法，来自适应调整测量噪声协方差，以提高滤波精度；文献[7]利用新息自适应估计过程噪声和测量噪声的协方差矩阵，以达到提高滤波性能、防止滤波发散的目的。综上可知，改进卡尔曼滤波算法的关键在于如何最优估计噪声统计特性，以此来提高卡尔曼滤波精度和防止滤波发散。但对于实际的非线性系统，很难获得精确的噪声统计特性来建立系统模型，这就需要综合考虑系统模型和噪声统计特性，来提高卡尔曼滤波的普适性和滤波精度[8-9]。因此，本文从系统建模的角度，提出一种基于新息的自适应 Kalman 滤波算法。

1 构建脱靶量模型

1.1 脱靶量定义

脱靶量在严格意义上表征为射弹与目标之间的最小矢量距离。但是在实际应用中，通常分为二维脱靶量和三维脱靶量，二维脱靶量主要包含高低角误差和方位角误差，三维脱靶量主要包含方位角误差、高低角误差和距离误差[10]。为便于后续需要实现闭环控制，本文采用的是二维脱靶量，即研究方位角误差和高低角误差。因为同一高炮武器系统设备引起的射击误差分量的相关系数和均方差属性相同，所以本文以某一方向的脱靶量(高低脱靶量)进行研究，同样的研究方法适用于另一方向的脱靶量(方位脱靶量)。

假设弹目矢量距离最小时的弹丸坐标和目标坐标分别为(x,y,z)和(xe,ye,ze)，则脱靶量高低角φe和脱靶量方位角αe的计算公式如下：

(1)

(2)

1.2 脱靶量分解

脱靶量偏差是弹丸位置的实际值与理想值之差，射击误差是弹丸位置的理想值与实际值之差，故将脱靶量的始点与终点对调后的矢量称为射击误差。射击误差的分解也就是脱靶量的分解。

脱靶量是各类误差的综合反应结果，为了更好地校正误差，需要对产生脱靶量的误差进行分解，依据武器系统各阶子系统的阶序，逐步找出导致脱靶量的所有原始误差(误差源)所在的部位与产生的原因，为建立误差源与脱靶量间的数学模型，进一步论证、设计、检测武器系统的脱靶量及其各个分系统的误差指标奠定技术基础[11]。

本节从产生原因和统计特性两个方面对误差源进行分析，根据分析结果进行分解与建模。

1)按产生原因分解误差源

依照武器系统各阶子系统的阶序，找出导致产生脱靶量的所有原始误差所在部位与产生原因，将其分解为以下四部分，图1所示为脱靶量传递过程。

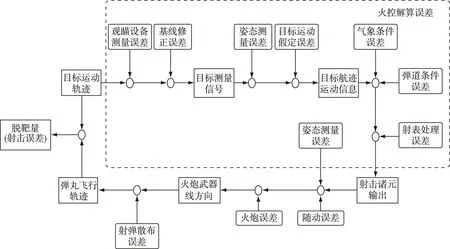
图1 脱靶量传递过程

①火控解算误差

其主要包括气象条件误差、弹道条件误差、基线修正误差、目标运动假定误差、射表处理误差。

②随动误差

其包括：对于人工操炮的武器系统，由于操炮手不能实时准确地跟踪火控系统解算出的射击诸元而导致的误差；对于采用随动系统实现自动跟踪的武器系统，由于在实现实时跟踪时，驱动轴间存在间隙、摩擦等因素而导致的误差。

③火炮误差

其主要包括火炮静态误差和火炮动态误差。火炮静态误差，即火炮与目标均静止时，火炮的调平、对正误差；火炮动态误差，即火炮的运动未加检测或虽加检测、调平、对正，但未调整到位所导致的误差。

④射弹散布误差

在上述三种误差为零的情况下仍出现的弹目偏差。

2)按统计特性分解误差源

误差源可以通过对射击误差的递阶分解得到，各种误差源导致的射击误差所具有的随机特性有明显区别。如果依据统计特性将前述的误差源进行分类，可以分为不相关误差、强相关误差、弱相关误差、系统误差。

各误差的状态方程及组成情况如下：

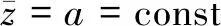
(3)

构成系统误差的误差源是射表处理误差。

②强相关误差xq状态方程

(4)

构成强相关误差的误差源是气象条件误差，弹道条件误差，基线修正误差。

③弱相关误差xr状态方程

(5)

构成弱相关误差的误差源是观瞄设备测量误差，操炮误差，目标运动假定误差。

④不相关误差xb状态方程

(6)

构成不相关误差的误差源是射弹散布误差。

1.3 射击误差数学模型

基于前面误差的分析与归类，可将射击误差(脱靶量)序列的状态方程与输出方程归纳为：

(7)

其中：

xr(k)=(xr(k),xr(k-1),…,xr(k-N+1))T

(8)

N表示脱靶量模型的阶数，表示k时刻状态只与前N个时刻相关。

1.4 脱靶量序列生成

对误差源参数进行设置，叠加生成脱靶量序列，射击误差分量的均方差及相关系数如表1所示。因为认为同一高炮武器系统设备引起的射击误差分量的相关系数相等，且均方差也一样，所以方位脱靶量与高低脱靶量特性一样，本文针对某一方向的脱靶量(高低)进行的研究。在Matlab中进行仿真得到脱靶量序列，假设弹丸发射时间间隔为20 ms，脱靶量时间序列如图2所示。假设火控系统的第k次射击误差满足：

X(k)=a+xq(k)+xr(k)+xb(k)

(9)

不相关误差、强相关误差、弱相关误差、系统误差的射击误差分量均方差及其相关系数的设定如表1中数据所示。

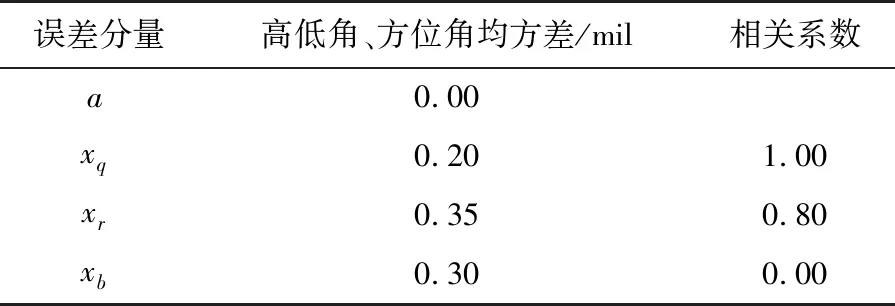
表1 射击误差分量均方差与相关系数

根据前述的射击误差模型建立以及对误差分量均方差值、相关系数的设定，在Matlab中生成射击误差序列如图2所示。

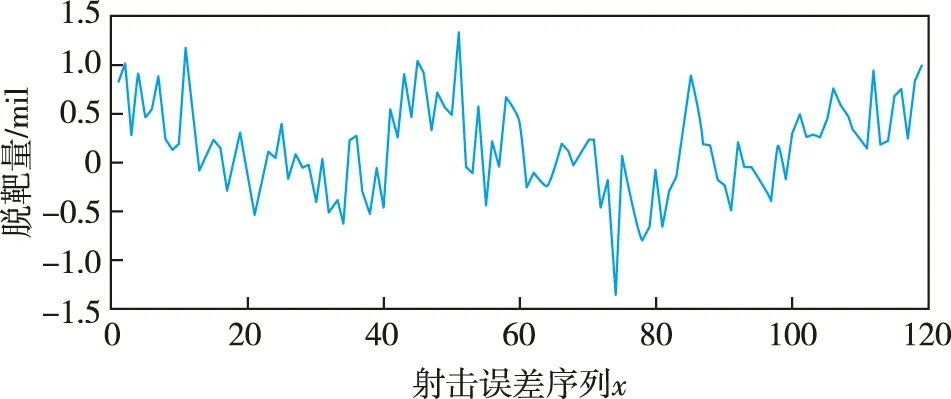
图2 射击误差序列图

2 构建各阶次预测模型及相关系数辨识

脱靶量预测模型的建立与阶次状态有关[11-16]。

2.1 建立脱靶量预测模型

1)脱靶量的一阶预测模型，即表示k时刻脱靶量只与前一个时刻相关。

(10)

2)脱靶量的二阶预测模型，表示k时刻脱靶量只与前两个时刻相关。

(11)

3)脱靶量的三阶预测模型，即表示k时刻脱靶量只与前三个时刻相关。

(12)

2.2 自相关系数辨识

两者之间的相关性会受到中间变量的影响。在考虑这些因素时即为自相关，xt时刻与xt-q时刻的自相关系数表示为

(13)

3 自适应新息卡尔曼滤波

3.1 离散系统卡尔曼滤波状态方程

离散卡尔曼滤波基本公式可参考文献[8-9]，本文不作详细描述。

(14)

其中，Xk为被估计量，Φk|k-1为状态转移矩阵，Γ(k)为系统噪声矩阵，ωk-1为k时刻系统噪声矩阵，Vk为k时刻测量噪声，Hk为观测矩阵，Yk为k时刻量测向量。

3.2 传统卡尔曼滤波预测算法

离散型的传统卡尔曼滤波算法具体步骤如下：

假设系统的过程噪声和量测噪声都是均值为零且互不相关的高斯白噪声，其k时刻协方差矩阵分别为Q、R。

1)计算滤波状态预测

(15)

2)计算其相应的预测协方差

P(k|k-1)=Φ(k)P(k-1|k-1)Φ(k)T+

Γ(k)QΓ(k)T

(16)

随后卡尔曼滤波结合了量测信息与预测信息再次更新了状态信息，基于最小方差的原则实现状态更新。

3)计算滤波增益矩阵

K(k)=P(k|k-1)H(k)T*

[H(k)P(k|k-1)H(k)T+R]-1

(17)

4)计算k时刻状态估计

(18)

5)计算k时刻估计误差方差

P(k|k)=[Ι-K(k)H(k)]P(k-1)

(19)

3.3 自适应新息卡尔曼滤波预测算法流程

在卡尔曼滤波中是根据预测递推方程来进行迭代预测，这将造成一定程度的延迟性。卡尔曼滤波中的噪声协方差包括过程噪声协方差矩阵Q和测量噪声协方差矩阵R。实际应用中的Q和R往往是不固定的，常采用默认值和经验值。Q和R的精确度会影响卡尔曼滤波的性能，本文采用新息来自适应估计Q和R。

1)计算k时刻新息

(20)

2)计算k时刻新息协方差

C(k)=H(k)P(k|k-1)H(k)T+R(k)

(21)

3)更新计算新息的过程噪声协方差矩阵

由式(17)和式(19)可推出Q(k-1)的表达式，稳定滤波时均方误差估计趋于0，所以，Q(k-1)≈K(k)H(k)P(k|k-1)，将式(21)代入式(18)，得基于新息的过程噪声协方差矩阵Q的自适应矩阵为

Q(k-1)=K(k)C(k)H(k)K(k)T

(22)

4)更新计算测量噪声协方差矩阵

由式(22)变形可得基于新息的测量噪声协方差矩阵R的自适应矩阵为

R(k)=C(k)-H(k)P(k|k-1)H(k)T

(23)

5)迭代计算

将考虑新息得到的式(22)和式(23)，代入式(16)至式(19)中进行迭代计算，在一定程度上可以解决噪声统计带来的问题，从而提高脱靶量预测的精度。

本文设计的自适应新息卡尔曼滤波流程图如图3所示。

图3 自适应新息卡尔曼滤波流程图

4 仿真结果与分析

同一高炮武器系统设备引起的射击误差分量即方位脱靶量与高低脱靶量的相关系数、均方差相似，因此，这里着手于高低脱靶量的研究，同样的研究方法适用于方位脱靶量。

本文采用的样本数据经验证均是符合脱靶量序列特性的平稳序列。给定的脱靶量序列如图4所示，随机脱靶量序列则根据上述分析得到的各个误差源特性叠加生成。随机脱靶量序列在后续仿真中一一展示。

图4 给定脱靶量序列图(120发弹丸脱靶量)

4.1 给定脱靶量序列时预测结果对比分析

根据给定的脱靶量序列，分别在传统卡尔曼滤波算法和自适应新息卡尔曼滤波算法中进行仿真[17-18]。预测递推步数的选取为2，预测模型分别为一阶脱靶量预测模型、二阶脱靶量预测模型和三阶脱靶量预测模型。用已知的90个弹丸脱靶量预测后续30发弹丸脱靶量，预测结果分别如图5～7所示。

图5～7中，蓝色星号折线代表给定脱靶量序列，红色圆圈折线代表各阶次多步传统卡尔曼滤波算法的预测结果，黄色菱形折线代表各阶次多步自适应新息卡尔曼滤波算法的预测结果。

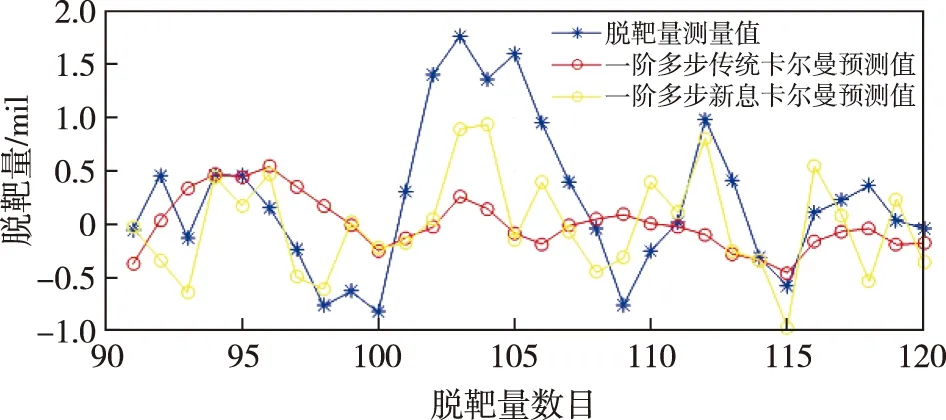
图5 一阶模型预测结果对比图

图6 二阶模型预测结果对比图

图7 三阶模型预测结果对比图

表2、3、4中的数据为给定脱靶量序列时各阶脱靶量递推预测模型的统计特性。

表2 一阶模型预测精度统计表

表3 二阶模型预测精度统计表

表4 三阶模型预测精度统计表

从上述的仿真结果对比图以及特性统计表中，可以得出以下结论：

1)在一阶预测模型、二阶预测模型和三阶预测模型中，自适应新息卡尔曼滤波算法的精度一直高于传统卡尔曼滤波算法。

2)在预测过程中，自适应新息卡尔曼滤波算法的预测结果与给定脱靶量之间的误差逐渐减小。因为，在自适应新息卡尔曼滤波过程中，过程噪声矩阵和量测噪声矩阵会根据之前的预测结果自适应修正。

3)随着脱靶量预测模型阶次的增大，它的预测误差的均值增大，但是变化的幅度不是很大，均方差的变化也不大，趋于平稳。可以得出结论：k时刻脱靶量与k-1时刻脱靶量的相关性比较大，与k-2时刻乃至更早时刻的相关性有所减少(k≥3)。

4.2 随机脱靶量序列时预测结果对比分析

在验证脱靶量模型随机情况下的仿真结果时，以一阶状态方程单步递推预测为例，假设已知前90发弹丸的脱靶量，预测第91发到120发弹丸的脱靶量。采用多次试验，随机选取三次试验结果进行分析。

图8为试验一的随机脱靶量序列示意图，图9为试验一的仿真结果图；图10为试验二的随机脱靶量序列示意图，图11为试验二的仿真结果图；图12为试验三的随机脱靶量序列示意图，图13为试验三的仿真结果图。

图8 试验一随机脱靶量序列图

图9 试验一仿真结果对比图

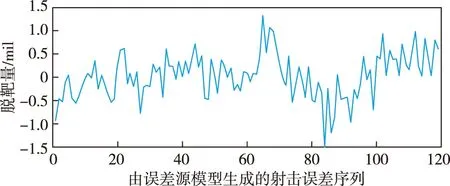
图10 试验二随机脱靶量序列图

图11 试验二仿真结果对比图

图12 试验三随机脱靶量序列图

图13 试验三仿真结果对比图

图9、11、13中，蓝色菱形折线代表由误差源叠加生成的随机脱靶量序列，红色圆圈折线代表传统卡尔曼滤波算法的预测结果，黑色星号折线代表自适应新息卡尔曼滤波算法的预测结果。

随机脱靶量序列时递推预测的统计特性如表5、6、7所示。

表5 试验一预测精度统计表

表6 试验二预测精度统计表

表7 试验三预测精度统计表

从上述的仿真结果对比图以及特性统计表中，除了可以得出和前节相同的结论之外，多次试验结果还表明：自适应新息卡尔曼滤波在工程应用中具有普适性且更加适用于低阶模型。

5 结束语

本文从提高脱靶量精度着手，提出了自适应新息卡尔曼滤波算法，建立了自适应新息卡尔曼滤波脱靶量预测模型，并且进行仿真验证。Matlab仿真结果表明，新息自适应卡尔曼滤波算法，在进行脱靶量预测时，与传统卡尔曼滤波算法相比，预测结果更加精确。同时，仿真结果也表明，在随机脱靶量模型中，自适应新息卡尔曼滤波算法预测精度也高于传统卡尔曼滤波算法，也证明了自适应新息卡尔曼滤波算法在弹丸脱靶量预测方面的应用普适性。