A Structural Damage Detection Method Using XGBoost Algorithm on Natural Frequencies
2021-12-18,
,
(1.Technology and Engineering Center for Space Utilization,Chinese Academy of Sciences,Beijing 100094,China;2.University of Chinese Academy of Sciences,Beijing 100049,China)
Abstract:Structural damage detection and monitoring are vital in product lifecycle management of aeronautic system in space utilization. In this paper,a method based on vibration characteristics and ensemble learning algorithm is proposed to achieve damage detection.Based on the small volume of modal frequency data for intact and damage structures,the extreme gradient boosting algorithm enables robust damage localization under noise condition of wing-like structures on numerical data.The method shows satisfactory performance on localizing damage with random geometrical profiles in most cases.
Key words:structural damage detection;ensemble learning;XGBoost;natural frequencies
Structural damage is intrinsic and it is prone to propagate because of the real environmental and mechanical factors in aeronautics structure. Detecting structural damage is vitally important for sustaining and preserving the service life of the structure. Numerous detecting techniques have been developed to provide practical means for the early warning of structural damage.
Structural Damage Detection (SDD) techniques can be classified into global and local methods.Compared to the local methods such as Ultrasonic Testing(UT),Acoustic Emission(AE),Radiographic Testing(RT),all vibration-based methods,considered as global methods,are easy to preform in practice. The principle of vibration-based SDD methods relys on the fact that structural damage causes reduction of the stiffness in the structure, which is associated with decreases in the natural frequencies and modification of the modes of vibration of the structure[1]. The key point to solve the inverse problem of structural damage detection is mapping the change in measurements between damaged and undamaged structure to the location and size of the structure. In the present study,we propose a SDD method using ensemble learning algorithms based on natural frequencies. As the application of ensemble learning,Extreme Gradient Boosting(XGBoost)[2]is seleted in our study to solve this mapping problem due to high accuracy and low risk of overfitting.
The rest of paper is organized as follows:we review the methods of structural damage detection in Section 1. The theoretical background consisting of proposed method is introduced in Section 2. Then numerical analysis and method verfication including result analysis are presented in Section 3. Finally,the conclusions are drawn in Section 4.
1 Literature Review
In the past decades,considerable effort has been put into vibration-based methods,and with emerging computing power and sensing technology in the last decade,Machine Learning (ML) and Deep Learning(DL) algorithms have become more feasible and extensive used in vibration-based SDD with elegant performance.
1.1 SDD Not Based on Machine Learning
Earlier methods relied on correlating structural damage to the changes in modal characteristics,which can be divided into time-domain algorithms and frequency-domain algorithms including but not limited to Complex Exponential Analysis (CEA)[3],Auto Regressive Moving Average (ARMA)[4],Frequency Domain Decomposition(FDD)[5].
More recently, Miguel et al.[6]developed a method combining Stochastic System Identification(SSI) modal identification with a harmony search algorithm. Ay and Wang[7]introduced a SDD technique depending on Auto-Regressive Moving Average with eXogenous input (ARMAX) models fitted to the measured signals.
1.2 SDD Based on Machine Learning
As an application of AI,ML algorithms have become very popular and broadly utilized in numerous vibration-based SDD methods,providing systems the ability to automatically learn and improve from experience. The most commonly used ML-based approaches are those that rely on modal characteristics such as natural frequencies and mode shapes as extracted features along with the feed-forward,fullyconnected, multi-layer Artificial Neural Networks(ANNs)or called Multi-layer Perceptrons(MLPs)as classifiers[8-10]. Other ML algorithms including Support Vector Machine(SVM)[11]and Principal Component Analysis (PCA)[12]have also been investigated for SDD.
1.3 SDD Based on Deep Learning
Compared to ML,the most attractive and important advantage of DL is that feature engineering can be ignored to some extent. Convolutional Neural Network(CNN)has been used as state-of-art model in some civil areas,especially 1D-CNN.
Yu Yang et al.[13]proposed a deep CNN(DCNN)based method,choosing Fast Fourier Transform(FFT)to transform time-sequence signals into frequency domain features,which are emerged into a 2D feature matrix as the inputs of the DCNN. Abdeljaber et al.[14]designed a real-time SDD system using 1D CNNs with high accuracy.
2 Theoretical Background
The architecture of proposed XGBoost-based SDD method is shown in Fig. 1.
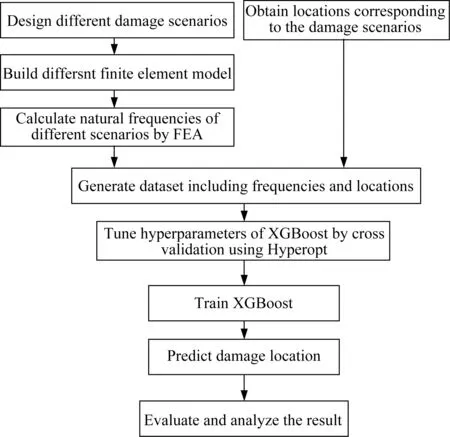
Fig.1 The architecture of proposed method
2.1 Modal Dynamics and Eigenvalue Problem
Modal analysis in structure mechanics is to determine the natural mode shapes and frequencies of an object or structure during free vibration.

whereΦis the eigenvector,namely,mode shape andωdenotes natural frequency of the system. For vibrational modal analysis,the damp is mostly ignored.

whereMis the mass matrix andKis the stiffness matrix. We seek a solution ofU,which results in the eigenvalue problem

Finite Element Method (FEM) can be used to perform this analysis[15]. Solving this eigenvalue problem,we get eigenvalues which represent the natural frequencies of the system.
2.2 XGBoost Algorithm
XGBoost is a boosting algorithm based on gradient tree boosting, which integrates addictive trees to approximate the output.
Considering a dataset withnsamples andmfeatures

where

XGBoost useskadditive trees to predict the output. The predictioncan be calculated as follows:

wherefkis an independent Classification and Regression Tree (CART),F is the space of all CARTs in the following form:

whereqrepresents the structure of each tree mapping an examplexito the leaf index.Tdenotes the number of leaves. Eachfkcorresponds to a tree structureqand leaf weightsw. In order to learnfk,the regularized objective function consisting of loss function term and additional regularization term will be minimized:

2.3 XGBoost-based Detection Method
Based on Section 2. 1 and 2. 2,the proposed method can be divided into three stages,including dataset builting,model training and damage detection.
2.3.1 Dataset Builting with Numerical Analysis
Finite Element Analysis(FEA)is used to calculate the eigenvalue problem as mentioned in Section 2. 1,obtaining natural frequenciesωof the structure. To treat SDD as a pattern recognition problem,the structure is divided into several zones to represent specific locations as shown in Fig. 2.
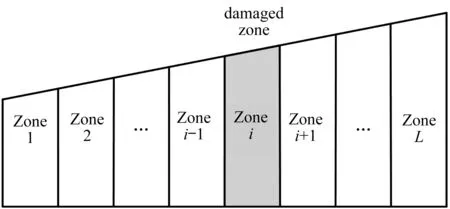
Fig.2 L Zones of the structure
By builting different finite element model associated with specific damage scenarios,a set of natural frequencies of damage scenarios is calculated which composes the dataset.

where

In Eq.(10),yiis the zone number of damaged structure. By setting different damage severity with different stiffness reduction of the structure,we bulid the dataset includingNtraintraining samples andNtesttesting samples. Furthermore,in order to study the noise robustness of the proposed method,noise is added into frequencies as well. The noise level is set to be 1% and 5%. The equation of noise contaminated in modal parameters is formulated as follows:

wherernandrcalare modal parameters with and without noise,respectively.Lnis the noise level.Rnis a random variable generated with uniform distirbution in the interval of [ 0,1].
2.3.2 Model Training
Before training model with training set,normalization is vitally important and reliable in most machine learning tasks. In this method,caculating the ratio of damage is the process of normalization,

whereωIis the natural frequencies of intact structure andηiis the ratio of damage.
XGBoost algorithm contains several parameters which can enormously influence the ability of the approximation. Not all parameters will be concerned in practical use,and some important parameters tuned in our study are presented in Tab. 1.

Tab.1 Parameters list of XGBoost
In order to improve the performance of the model,it is necessary to find the optimal parameters. In this paper, HyperOpt[16]is used to ajust the main parameters.
2.3.3 Damage Detection
In this section,the problem can be described as approximating the location ofi-th example with givenmnatural frequencies
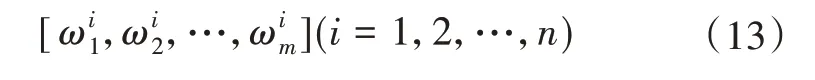
After training XGBoost algorithm with training set,we can use this model to predict the zone of damage location. To evaluate the performance of the proposed method,accuracy is selected

whereZONEiis the damage zone ofi-th sample and 1ZONEiis an indicator function.
3 Numerical Analysis and Method Verification
3.1 Numerical Modeling
XGBoost-based SDD method requires natural frequencies of different structural damage patterns including specific damage location and severity. To obtain adequate patterns,we calculate frequencies with finite element model as shown in Fig. 3.

Fig.3 The finite element model of wing-like structure
The wing-like structure is asymmetric with fixedfree boundary condition. Material properties of the intact wing-like structure are listed in Tab. 2.

Tab.2 Material properties of the wing-like structure
According to the actual mechanical properties of the wing structure,it is known that the structure damage mostly occurs in the wing spars and skins. Therefore,twenty-one potential locations are selected in this paper as shown in Fig. 4.

Fig.4 The wing-like structure FEM damaged at zone 5
The first five natural frequencies of the intact winglike structure and of the structure damaged at zone 5(30 percent reduction in the modulus of elasticity)are listed in Tab. 3 .

Tab. 3 First five frequencies for the intact structure and structure damaged at zone 5
Damage zones for test samples are more random as shown in Fig. 5. Subsequently,168 traning samples and 12 testing samples with first five frequencies are obtained without and with noise respectively.
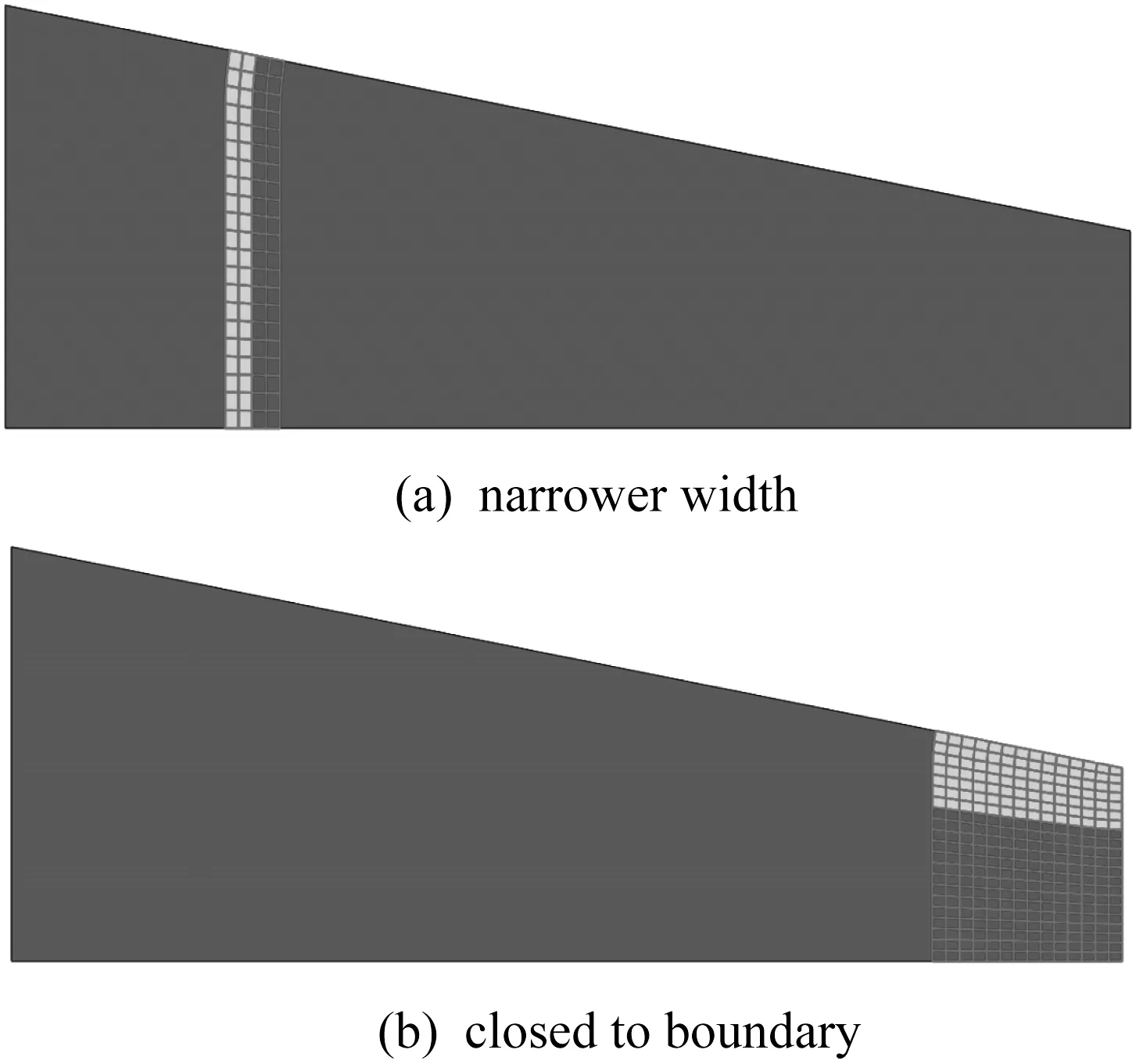
Fig.5 Two examples of damage patterns of test set
3.2 Damage Localization and Evaluation
After XGBoost is constructed for the wing-like structure damage location,the total of 168 damage samples generated by the 21 damage patterns can be used to train XGBoost. The accuracy of training set is 97. 6%. The results of XGBoost verification on test set are shown in Fig. 6 and Fig. 7. When the dot is on the black line,that is,the damage prediction zone and real damage parts overlap,the classification or detection is considered to be correct.
From Fig. 6,the detection of case 4 and 6 are wrong when noise is not added to the natural frequencies. Fig. 7 shows that the detection of case 4,6 and 11 are wrong when noise is added to natural frequencies. Compared to the cases without noise,only one case is mistaken by the proposed method,Therefore,the robustness of proposed method is verified. An overall result of accuracy on different level noise is presented in Tab. 4.

Fig.6 Result of proposed method on dataset without noise
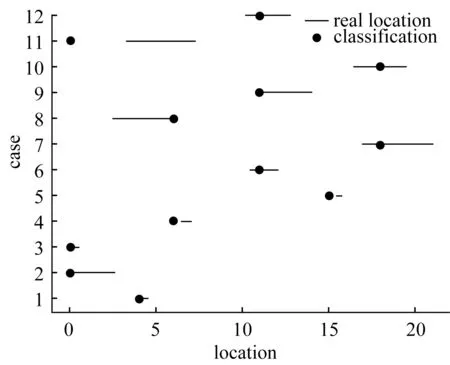
Fig.7 Result of proposed method on dataset without noise

Tab. 4 Accuracy on test set with different noise level
4 Conclusion
Taking the wing-like structure as an example,the method based on natural frequencies and ensemble learning algorithm XGBoost is applied to detect the wing-like structure damage. The result of XGBoost training and verification indicates that proposed method shows satisfactory performance on localizing structural damage with random geometrical profiles in most cases.It is expected that the conjunction use of vibration characteristics and gradient boosting can be promising for damage detection and health monitoring of aeronautic structures with relatively small volume of original data.
