不确定分布时滞系统的全局鲁棒滑模控制
2021-12-18田柳青
田柳青
(吕梁职业技术学院电子信息系,山西孝义 032300)
在工程控制系统中,常存在影响控制性能的因素。如时滞、外加干扰等。从被控对象建模来看,存在分布时滞,与事物的本质更加接近。如文献[1]提出的材料热加工采用的是具有分布时滞的抛物型系统。近几年,针对分布时滞系统的稳定性和控制等问题,各国学者对其进行了广泛的研究[2-7]。
滑模“结构”是不固定的非线性控制(SMC),具有设计简单、抗干扰、无需在线辨识等优点。所以经常用于控制分布时滞系统中。文献[8]中,分布时滞系统没有考虑系统参数不确定性的影响及设计的自适应滑模控制器抖振严重。文献[9]讨论的是含有分布时滞的2-型模糊系统,针对参数抖动设计了带有容错功能的滑模控制器。文献[10]所涉及的中立型系统,含有分布时滞,设计的滑模控制器没有涉及外部干扰的问题。
通常,传统SMC 中包含趋近和滑动两种模态。为消除趋近模态易受到不确定性的干扰,使系统状态始终保持在具有鲁棒性的滑动模态上,众多学者针对全局滑模控制进行了研究[11-14]。同时为了更好地解决被控对象外部干扰引起的系统不稳定问题,文献[15-17]引入自适应方法,通过自适应律实时估计外部干扰,自适应与滑模控制的结合改进了控制性能。
本文针对在状态时滞和分布时滞中同时存在不确定性因素以及外部干扰的一类复杂分布时滞系统,为实现整个控制过程都处在滑动模态阶段,设计了带初始状态条件的滑模面,使系统状态始终保持在具有鲁棒性的滑动模态上,实现全局滑模。为证明滑模稳定,其充分条件由Lyapunov 泛函结合Jensen 不等式与Schur 补,转换成LMI 的形式,方便求解。为解决外部干扰引入自适应方法,设计了自适应滑模控制器,仿真[18]说明了控制方法有效可行并降低了抖振。
1 系统描述及相关引理
考虑以下一类在状态时滞和分布时滞中同时存在不确定性因素和外加干扰的分布时滞系统:

其中,x(t) ∈Rn是状态变量,u(t) ∈Rm是控制输入。h1>0为状态时滞,h2>0为分布时滞。A0,A1,A2∈Rn×n为已知状态矩阵,B∈Rn×m为已知输入矩阵。ΔA0,ΔA1,ΔA2为不确定的系统参数矩阵。f(x,t) ∈Rn为系统外部扰动。φ(t) ∈Rn为连续的任意初始状态向量函数。
在全文做如下假设:
假设1对于被控系统(1),所有状态可直接测量。其中矩阵B列满秩,(A0,B)是完全可控的。
假设2不确定项ΔA0,ΔA1,ΔA2,f(x,t) 满足ΔA0=BE0,ΔA1=BE1,ΔA2=BE2,f=BF的匹配性条件。因此,记F],则系统(1)可化简为

假设3存在未知正常数q1,q2,满足

为证明滑模稳定性,需要下面的引理:
引理1[19](Jensen不等式)
给定实数α,β且α>β及正定矩阵S,则下列不等式成立,即

引理2[20](Schur补定理)对于对称矩阵:
则下面三个条件等价。
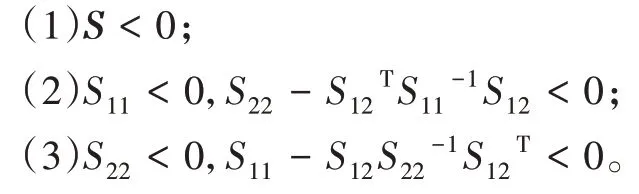
2 全局鲁棒滑模控制器设计
2.1 积分型滑模面设计
对于系统(1),构造如下的带初始状态条件的滑模面:

其中,D∈Rm×n为满秩常数矩阵,D的选择不唯一且满足DB是非奇异。待定常数矩阵K∈Rm×n。
对于任意初始条件x(0),消除了控制到达阶段,滑模面(4)都可以满足S(x(0),0) = 0。对式(4)求导并代入式(2)得

令S= 0,= 0,解出等效控制律为

将式(5)代入式(2),符合假设1 的理想滑动运动方程为
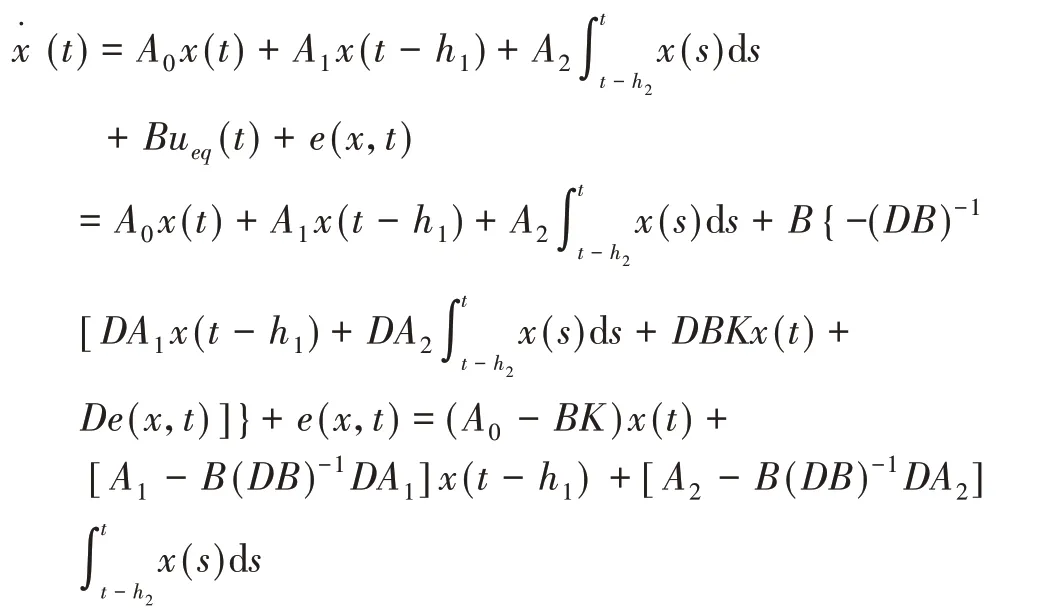
令

即理想滑动运动方程的简化形式为
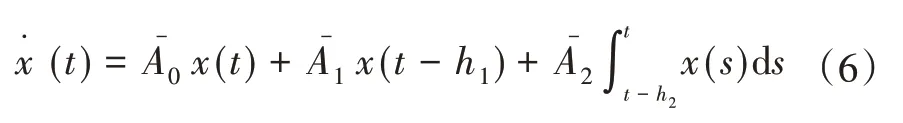
2.2 滑模稳定性分析及主要结论
定理1为证明滑模渐进稳定,使得下列LMI成立:

其中正定矩阵W,W1,W2是对称的,Q是适当维数的矩阵,K=QW-1是状态反馈控制增益。
且

证明:设计Lyapunov-Krasovskii泛函数为
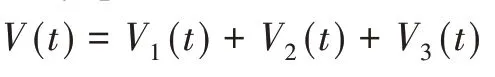
其中,

由引理1得:


其中,

由引理2得公式∑<0,则<0
等价于:

针对滑动模态,为满足其渐进稳定,令P-1=W,用分别左乘、右乘公式,则V·<0。证毕。
2.3 自适应全局鲁棒滑模控制
对于系统(1)设计自适应全局滑模控制器,即

控制律包括两部分,其中,ucon是连续部分,udis是不连续部分。则对于任意初始状态,在控制律(9)作用下系统(1)始终处在滑模面上。首先设计ucon,它等于原系统(1)对应的标称系统(2)在滑模面上的等效控制,即

下面设计udis。由系统的假设3,其中q1和q2是不确定性的上界,是未知的,取和为q1和q2的估计值,参数偏差为

根据滑模面选择适当的自适应律为

不连续控制律为

其中,ε为正常数。
将式(10)和(12)代入(9)即可得到完整的自适应全局鲁棒滑模控制律,即

定理2对于在状态时滞和分布时滞中同时存在不确定性因素以及外部干扰的分布时滞系统(1),在有限时间内,控制律(13)能保证状态保持在积分滑模面(4)上。
证明取Lyapunov函数

沿着式(2)对其求导,得

所以

证毕,即满足有限时间内,系统(1)在控制律(13)的作用下到达并稳定于滑模面(4)上。
由于控制律(13)中符号函数可能导致严重的抖振,饱和函数为

代替符号函数可以得到降低抖振的自适应全局鲁棒滑模控制律,即

3 仿真实例
考虑系统(1),参数如下:
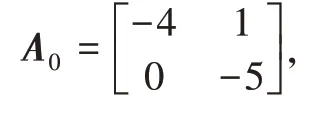

通过MATLAB工具箱,求解LMI(7)-(8),得

解得

滑模面为

控制律(13)为

控制律(15)为
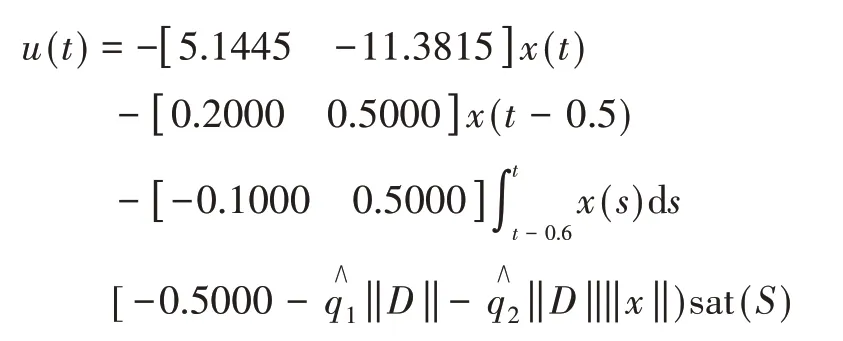
设初始条件为x(t) = [ 0.5 1]T,t∈[ -0.6,0 ]
在控制律(13)的作用下自适应参数、状态、滑模面、控制律,仿真结果如图1-5。

图1 控制律(13)作用下的xFig.1 x with control law(13)

图2 控制律(13)作用下的SFig.2 S with control law(13)

图3 控制律(13)作用下的uFig.3 u with control law(13)

图4 控制律(13)作用下的q1Fig.4 q1 with control law(13)

图5 控制律(13)作用下的q2Fig.5 q2 with control law(13)
在自适应全局鲁棒滑模控制律(15)的作用下自适应参数、状态、滑模面、控制律,仿真结果如图6-图10。

图6 控制律(15)作用下的xFig.6 x with control law(15)

图10 控制律(15)作用下的q2Fig.10 q2 with control law(15)
由图1-5 仿真结果表明,在控制律(13)的控制下,状态x、滑模面S、控制律u抖振严重,控制性能差。通过对比,图6-10 所设计的自适应全局鲁棒滑模控制器(15)减小了控制抖振,图6 中系统状态曲线更加平滑,响应速度更快。图7 表明在响应的全过程,消除了控制的到达阶段,改善了动态性能。图8 表明控制律降低了抖振。通过MATLAB 仿真,结果显示控制方法有效可行。

图7 控制律(15)作用下的SFig.7 S with control law(15)

图8 控制律(15)作用下的uFig.8 u with control law(15)

图9 控制律(15)作用下的q1Fig.9 q1 with control law(15)
4 结论
针对在状态时滞和分布时滞中同时存在不确定性因素以及外部干扰的一类复杂分布时滞系统,本文采用全局滑模的思想,设计了带初始状态条件的滑模面,消除了传统滑模控制器中的到达模态,提高了鲁棒性能。通过合理构造自适应律解决了外部干扰的问题。用饱和函数降低系统抖振,曲线更加平滑,仿真结果验证了本文提出的全局鲁棒滑模有效可行。但分布时滞系统结构复杂,控制起来比较困难,其实际的控制方法与稳定性能需进一步研究。
