培养问题意识，提升数学自主探究能力

钱云

小学生思维活跃，充满想象力，对生活和未知领域充满好奇和疑问。教师要结合小学生的年龄特点，在小学数学教学中，引导学生的思维方向，鼓励学生在学习过程中敢于提问、善于提问，及时解决思维困惑和数学难题;通过提问的方式集中学生专注力、提高数学学习兴趣，让学生体会到主动参与课堂教学带来的成就感，从而促进学生产生探索数学的欲望。对此，笔者结合日常教学经验，提出四种授课方式：针对学生独到见解，要求继续向深处研究探讨;在学习过程中寻求不同的答案，培养学生的逆向思维;借用生活原型，训练学生的观察能力;以数学实验为基础，鼓励学生大胆猜测。通过上述方式，改变了以往教师讲、学生听的模式，让学生成为课堂的主人。

一、针对独到见解，深处追问

小学生虽然年纪小，对数学的理解能力有限，但依然不乏学生学习能力比较强，针对某些题目有自己独到的见解，并且这些见解已经初步具备数学逻辑原型。教师应在授课过程中及时抓住这些见解，引导学生继续开展逻辑思维，采用自问或者他问的方式向深处探讨追问，从而激发学生主动探索的欲望，培养学生主动探索的能力。

例如，学习了“长方体和圆柱体”后，教师准备教具，要求长方体的底面积等于圆柱体的底面积，二者等高。现在有一个大的水槽，水槽中盛满水，分别把长方体和圆柱体浸入水中，问溢出水的体积是否相同？如果把圆柱以底面直径为分界线，垂直对半切开，把长方体均分成两个长方体，把圆柱的一半和长方体的一半投入该水槽中，溢出的水是多少？

针对该问题，学生开始思考：溢出水的量和什么有关系？有的学生指出长方体投入水槽中，意味着长方体将水槽中的水“赶”出去了，那么溢出水的体积应该刚好就是长方体的体积。对于圆柱体也是一样的思维。那么二者溢出水量的计算，也就转化为二者体积的计算比较，那么二者体积又呈现什么关系呢？学生通过计算，发现二者体积相同，意味着溢出水的量相同。在第二问中，二者都是将一半体积投入水中，很容易得出溢出水的量依然和上问中单独投入时溢出的量相同。

教师继续追问，如果将与圆柱等底等高的圆锥投入水中，溢出水量呢？学生思考回忆这些物体的体积计算公式以及相互关系，从而计算出答案。

针对问题的不同变形，有部分学生可以快速理解数学内涵并有独到见解，教师在顾及全体学生接受知识的同时，适当对反应快速的学生进行深入追问，从而形成你追我赶的课堂模式，大家争相思考探索，营造和谐、高效的课堂氛围。

二、寻求不同答案，逆向思维

逆向思维是数学解题常用的思维方法。小学阶段培养学生的逆向思维有一定的挑战，需要教师结合学生的年龄特点和教材内容，引导学生从不同角度提出问题，寻找问题的不同答案。借助逆向思维法则，帮助学生理解问题思路，激发学生主动探索的欲望。

例如，学校组织开展兴趣小组活动，参加活动的男生有40人，参加活动的女生人数是男生人数的2/5，求该小学一共有多少人参加该兴趣小组活动？

教师先引导学生仔细读题，要求学生明确题目中的条件和问题，学生理解题意后从问题开始着手思考，要求一共多少人参加活动，必须知道参加活动的男生和女生人数，男生人数题目已知，如何求解女生人数呢？学生自己回答，借助男女生人数的比值可以算出女生人数。

总人数计算公式为：40×2/5+40

有的学生另辟蹊径，认真思考题目中的比例关系。指出这道题既然是求总人数，上述方法是通过男女生相加的方式计算，那么是否可以借用男女生比值的关系计算男生人数和总人数的比例关系，直接计算得到总人数呢？学生开始思考，女生人数是男生的2/5，假设男生人数是1，那么总人数就是1+2/5=7/5，学生开始提问，总人数比值的含义是什么，是男生人数/总人数的比值呢，还是总人数/男生人数的比值？学生通过绘制逻辑结构图，领悟7/5的比值关系，计算出总人数。

逆向思维解题模式，可以将试题简单化，而运用逆向思维要求学生一题多解，则培养了学生认真思考、逻辑判断的习惯。为了防止学生在思维过程中出现盲区或者进入“死胡同”，教师应要求学生以自我提问或者对他人提问的方式进行题目探究，以及时纠正思维方向，解出正确答案。

三、呈现生活原型，科学观察

呈现生活原型、借助生活情境是小学数学常用的教学方法，旨在借助学生熟悉的事件或物品，让学生在熟悉的环境中思考新的问题，激发学生发现和探索的欲望，给学生以生活的启迪，从而完成专业数学知识的学习。由于小学生不具备相应的思维能力，导致他们在学习过程中会忽略细节问题，所以需要教师引导，培养学生的问题意识及观察的能力，从而提高学生自主探究能力。

例如，教学“认识物体”时，教师将皮球、牙膏盒、茶几、电视、碗等带入课堂，学生发现这些都是生活中常见的物品，甚至是天天接触的物品，但是从未想过将这些和数学中的专有名词结合。首先从物体名称引导，这些物品叫什么名字呢？它们的形状相同吗？学生观察后提出问题，长方形和正方形有什么不同？长方体和正方体呢？皮球到底是圆形还是球形的？太阳是圆形的还是球形的？什么是圆形？什么是球形？皮球可以装进一个正方体盒子中，是不是意味着正方体可以切割成球体？碗口和碗底都是圆形，但是大小不一样，又是什么形状？学生在提问过程中仔细观察每个模型的异同，认识常见生活物品形状的数学学科术语，在学习过程中，培养了学生科学观察的能力。

利用生活物体的原型引导小学生学习数学，培养学生主动观察和思考的习惯，在思考过程中产生问题，在寻找真理的过程中掌握数学知识，简化了数学难度，丰富了学生的想象。同时，上述理论和实际相结合的授课模式，为学生提供了数学学习的新途径，让学生在熟悉的生活中寻找数学知识和规律，从而将被动学习转化为主动探索。

四、组织实验活动，猜测验证

小学数学实验课程在数学教学中占据重要地位，可以将虚拟的数学计算和逻辑思维实体化。在实验过程中，通过设计合理的实验操作流程，引导学生动手的同时积极动脑，学习和娱乐相结合，知行合一。教师引导学生合理假设实验结果，并通过实验验证猜测结果，以引发学生对数学实验的兴趣。借助数学实验，开阔学生数学视野，拓宽数学教学思路，同时提高数学教学效率。

例如，给定平行四边形，如下图1，要求学生计算面积。

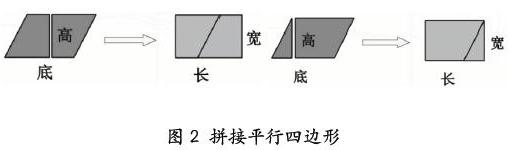
该图形和之前学习过的长方形、正方形不同，但又有相似的地方。那么如何进行面积计算？学生提出，按照长方形计算面积的方式，两个邻边的乘积为面积。有学生提出，计算方法不对，不管是正方形还是长方形，两个邻边的关系都是垂直的，但平行四边的邻边不垂直。有的学生將平行四边形进行裁剪拼接，将其拼接为长方形，再测量长、宽，然后计算面积。如下图2所示。学生在拼接过程中，发现平行四边形可以剪裁成不同的形式，如果平行四边大小形状完全相同，那么在其底边不同位置裁剪，是否改变面积大小？裁剪后的平行四边形底边长是多少？宽又是多少？学生通过测量，发现不管在什么位置裁剪，其底边和宽的长度都不变。学生继续提出疑问，那么裁剪后图形的底边和原来平行四边形的底边有什么关系呢？

有的学生为了防止裁剪失误，将平行四边形框在固定大小的格子中，但发现平行四边形的边是斜的，意味着在数格子时，出现了大半个格子被占或者小半个格子被占的情况，他们发现单纯挪格子可能会导致结果出现错误，学生再次陷入思考中。

通过组织实验活动，培养了学生积极动手的习惯;通过实验——猜想——验证——提问——验证的方法，培养了学生的问题思维;通过问题引导，激发学生主动探究的欲望，在探究中思考，在思考中寻找正确答案，循环往复，将被动听、记的数学课堂转变为主动探索、寻求真理的过程，开发了学生的数学思维，也培养了学生好问的品质。

小学生是“十万个为什么”，在进行提问式课堂教学中，教师应引导学生的思维方向，鼓励学生提问，培养学生的数学逻辑思维，同时掌握课堂内容和教学效果，防止课堂节奏严重偏离预期，从而帮助学生更快、更好地掌握相应的专业知识。