超声复合电解加工与抛光的振动系统优化

王 芳，孙延普，孙希强，王 见，朱玉全

（临沂科技职业学院，山东 临沂 276000）

1 超声振动系统动力学分析

1.1 超声振动系统模型建立

超声振动系统理论设计的建立，一般采用共振设计法和整体共振设计法两种方式[1]，单独采用其中一种方式时，振动系统设计频率与工作频率20 kHz差距较大，综合考虑压电换能器采用共振设计法，指数型变幅杆与工具电极采用整体共振设计法，让这两部分各自工作频率接近于系统工作频率20 kHz。设计要求：压电换能器额定功率500 W、激振电压200 V，工作频率20 kHz左右时，压电换能器端面输出振幅达到10 m左右，指数型变幅杆大端面直径D1=30 mm，小端面直径D2=16 mm；工具电极实际工作长度l2=26 mm，大端面直径d1=12 mm，小端面直径d2=10 mm。压电换能器、指数型变幅杆中各组成部分的材料、密度等参数如表1。

表1 超声系统各部分材料参数

如图1，超声复合电解加工系统主要由超声加工部分、电解加工部分、工作台进给部分、测量部分等组成。工作原理：电源接通，超声波发生器发出交变电信号，通过压电换能器转换为机械振动并放大，随后指数型变幅杆及工具电极进一步将振幅放大，满足加工要求。加工过程中，工件表面的深度不断加深，为实现工件和工具电极之间恒定的微压力，工作台在弹簧和磁极对的作用力下不断进给[2]。

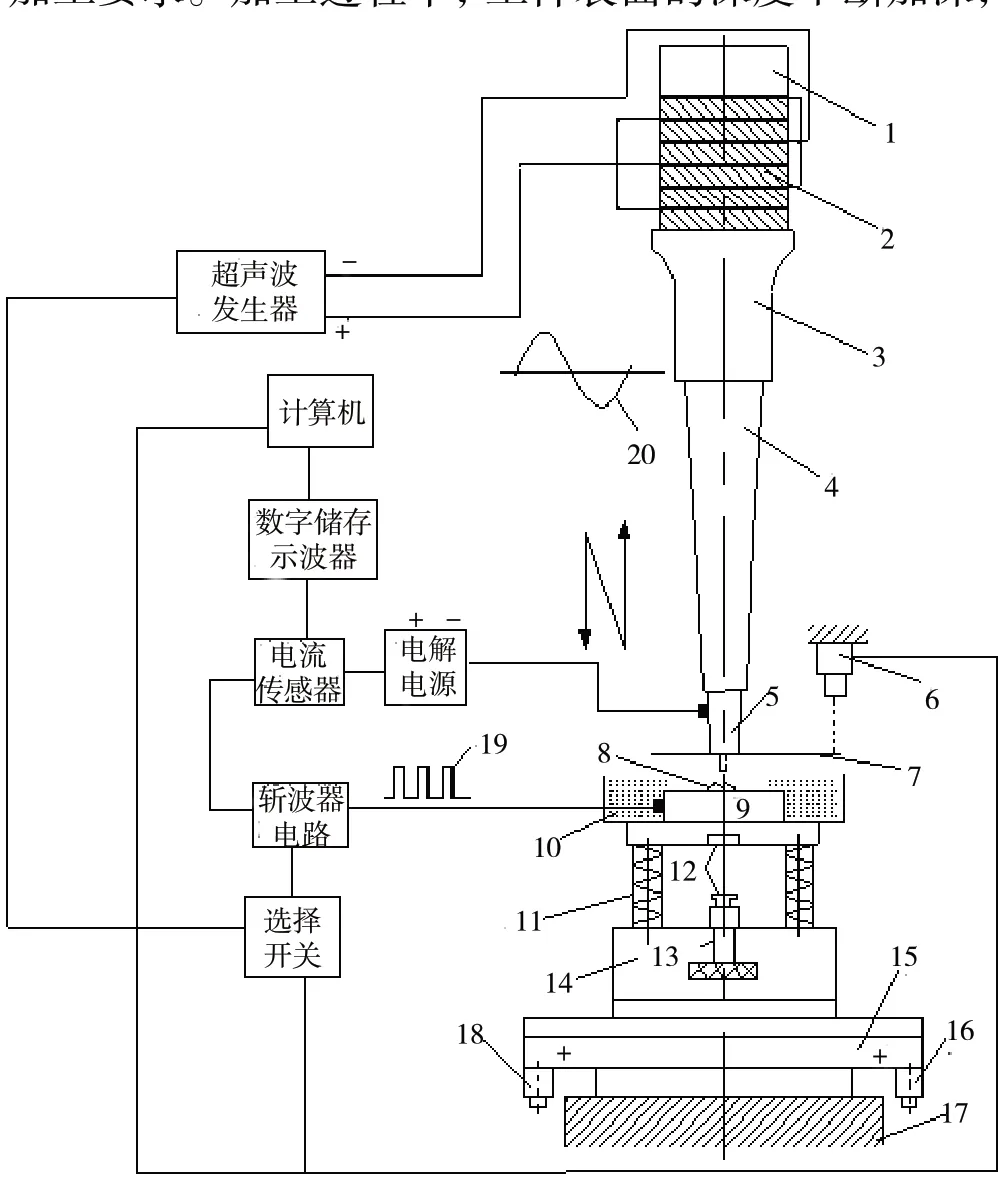
图1 超声复合电解加工系统图

1.2 超声振动系统模态分析

超声振动系统动力学分析包括模态分析与谐响应分析，首先通过分析模态分析，得到超声振动系统在20 kHz附近的纵振模态，为设计超声振动系统提供理论依据。超声振动系统是轴对称图形，为简化运算，提高效率，采用四分之一简化模型[3]。采用自下而上方式构建模型，建模时只考虑形状和大小，忽略其他因素，指数型变幅杆与压电换能器、指数型变幅杆与工具电极均采用无螺纹连接，认为压电换能器为实心圆柱体，不考虑预应力螺栓、电极片的因素。

对于超声振动系统模态分析来说，电路状态是唯一约束条件，在压电换能器压电陶瓷晶片的正极表面和负极表面分别施加0 V电压，因为超声振动系统模型只有四分之一，需对模型施加xoz面和yoz面的对称约束，采用分块Lanczos方法求解，频率范围设置为10 kHz～30 kHz，提取前7阶模态。

电源接通后，超声波发生器把发出的交变电信号传递给压电换能器陶瓷晶片，压电换能器陶瓷晶片把交变电信号传递到前、后盖板，压电换能器从而作纵向振动，指数型变幅杆与工具电极接收到压电换能器的振动后，将振幅进一步放大，因此，超声振动系统的最大纵向振幅位于工具电极的小端面处。由图2可以看出，17.812 kHz、22.349 kHz为第一、二阶模态频率，利用谐响应分析选择出最佳的模态频率。

图2 超声振动系统模态分析振型图

1.3 超声振动系统谐响应分析

对于谐响应分析，当超声振动系统的纵振模态频率等于工作频率时，工具电极端面振幅达到最大，进行超声振动系统谐响应分析，可以得到工具电极的最大位移值、振动系统的应力极大点、位移节点等性能参数。

在压电换能器上加载正弦电压，模拟交变信号转换成机械信号，首先将模态分析后压电换能器中的陶瓷晶片正、负极上的电压U=0 V删除，使同一电极表面各节点等电势，其次命名正极为压电耦合部1，负极为压电耦合部2，在耦合部1的节点上施加电压U=200V，在耦合部2的节点上仍施加电压0 V[4]。

谐响应分析的分析类型Harmonic，设置求解频率范围1 525 kHz，求解子步stepped 设置为30步，采用Full计算方法，常数阻尼系数设置为0.3%，采用稀疏矩阵（Sparse）定义求解器。运算结束后进入后处理查看超声振动系统工具电极端面的纵向振动振动位移情况，如图3。

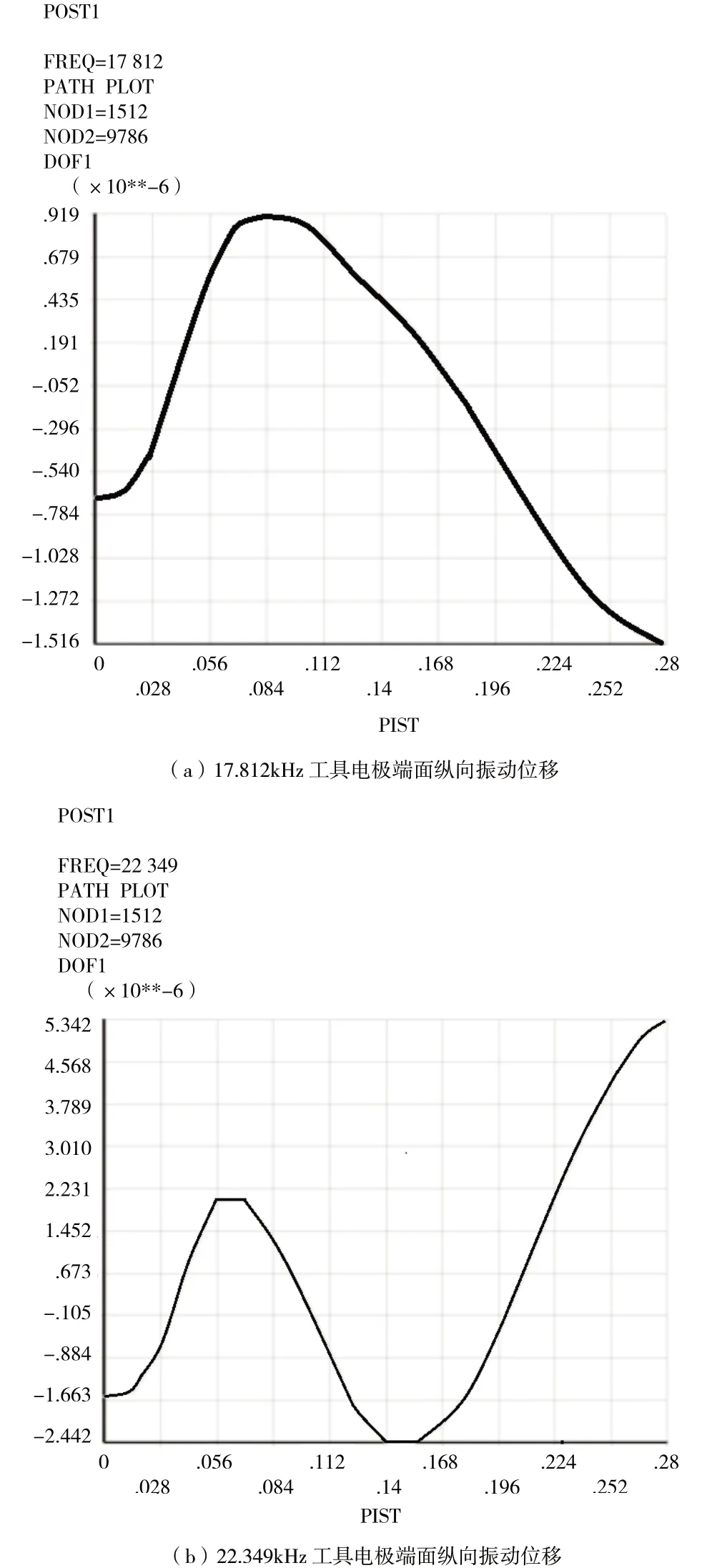
图3 超声振动系统工具电极端面纵向振动位移

超声振动系统存在两处振幅为0的节面，其中一处为压电换能器的压电陶瓷与前盖板的结合面，另一处为指数型变幅杆的位移节点位置[5]，由图3可知，频率17.812 kHz时，位移节面有两处等于0；频率22.349 kHz，位移节面有三处等于0，因此超声振动系统固有频率是17.812 kHz。

通过后处理器post26，提取工具电极表面中心节点9 786的Z向幅频曲线，如图4，在谐振频率17.812 kHz时，超声振动系统振幅达到峰值为30 m，这基本能满足超声复合电解加工振幅需要，但谐振频率17.812 kHz与工作频率20 kHz有一定差距，需要对超声振动系统的一些基本参数优化，以更好的完成加工。

图4 工具电极端面Z向幅频曲线图

1.4 超声振动系统优化设计

最优设计即最有效率的设计方案，可以通过优化物体形状、结构尺寸等方面（图5），达到工作需要。对于超声振动系统，采用缩短压电换能器前、后盖板长度，指数型变幅杆长度来的方式提高频率[6]。

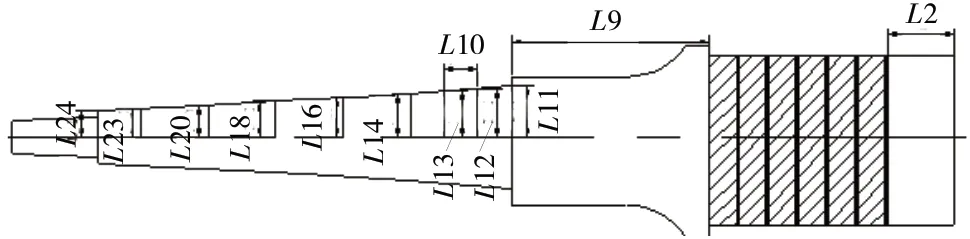
图5 优化后超声振动系统尺寸设计图

（1）建立循环所用的分析文件。参数化建模、动力学分析、添加约束、施加电压载荷、提出状态变量和目标函数等GUI操作都可以利用APDL命令流完成。

（2）进入优化处理器（OPT）。

①定义优化设计变量：

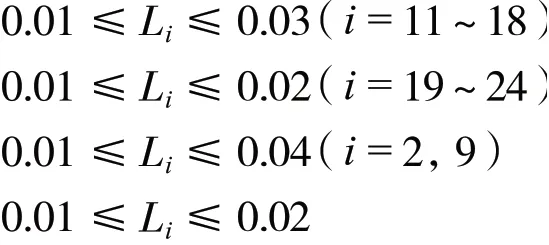
②定义优化状态变量：

③定义目标函数：

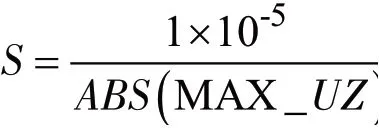
（3）选择优化方法。选择一阶优化方法，循环次数10。

（4）查看优化结果。包括设计序列结果和后处理POST26，优化后超声振动系统的频率和最大应力如表2。

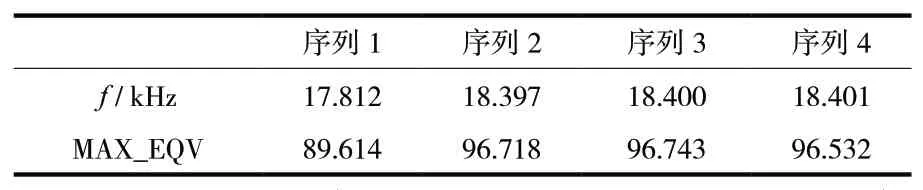
表2 超声振动系统的优化结果

由表2可知，序列1为优化前原始尺寸，序列2、3、4为优化后尺寸，其中序列2为最优序列，优化后固有频率提高到18.397 kHz，更加接近要求的工作频率20 kHz。优化完成后，将优化后的数据通过命令流的方式建模，再次进行超声振动系统动力学分析，如图6提取工具电极表面的幅频曲线。优化后工具电极端面的振幅达到31.2μm仍满足加工需要。

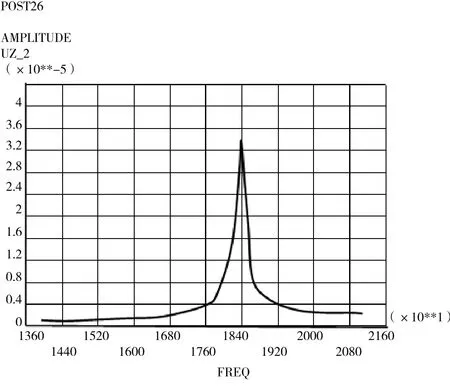
图6 优化后工具电极端面Z向幅频曲线

1.5 超声振动系统振幅检测

压电换能器、指数型变幅杆、工具电极、工作台、高精度激光微位移传感器、计算机分组成超声振动系统振幅检测装置。其中，高精度激光微位移传感器具有超高的采集速度，可直接测量工具电极端面振幅，振幅通过计算机显示出来。测量优化后的振动数值与理论分析值对比，验证理论分析的正确性，为制作超声振动系统提供理论依据。

检测过程：将该装置按图7（a）连接，试验过程中保持压电换能器功率500 W不变，超声振动系统频率设置在20 kHz。计算机采样、处理后，得到工具电极端面位移—时间曲线图7（b），通过该图可清晰看到工具电极端面最大振幅值。分析值与测量值对比结果如表3。

图7 超声振动系统振幅测量装置及检测结果

表3 超声振动系统的输出振幅

从图7（c）可以看出，采样得到的曲线形成效果好，工具电极端面的幅值大小可直观看出。通过表3可以看出，测量值达到32.35μm，这完全满足超声复合电解加工要求，将分析值与测量值对比发现，理论分析值在31.2μm，这也验证了动力学分析、优化设计的正确性。

1.6 超声复合电解抛光

对于四冲程内燃机，缸体是主要部件，是安装零部件和零配件的支撑骨架[7]，结构如图8。为保证安装精度，缸体在安装其他零部件前，主要表面、摩擦表面、润滑油道等要具备很高的清洁度，这就要求采用一种新工艺进行清洗四冲程内燃机缸体。

图8 四冲程内燃机缸体

超声复合电解抛光是集超声振动抛磨和电解加工优点的新工艺，这对于四冲程内燃机缸体的清洗来说是一种十分有用的镜面加工方法，技术难点在于如何使超声加工抛磨与电解加工相匹配，去除毛刺，从而获得较好的缸体镜面。

超声复合电解抛光的振动系统与超声复合电解加工振动系统类似，其动力学分析、参数优化过程不再赘述。超声复合电解抛光四冲程内燃机缸体试验目前还不是完全具备条件，故省略。

2 结论

（1）对于超声振动系统，压电换能器采用共振设计法，指数型变幅杆与工具电极采用整体设计法，既有创新性又更满足加工的要求。

（2）运用ANSYS软件中压电耦合模块进行动力学分析，得到工具电极端面的最大纵向振动位移值，并且满足加工要求，为进一步提高加工效率，进行尺寸优化设计，缩短了设计周期、降低了制作成本。

（3）利用超声振动系统振幅检测装置进行振幅检测发现，采用优化后的数据制作的超声振动系统更加稳定，工具电极端面的振动幅值也更加满足加工要求。

（4）冲洗四冲程内燃机缸体的难点在于超声加工抛磨与电解加工的匹配，这也是以后研究的重点。