纳米ZnO改性沥青分子动力学模拟研究

2021-12-17苏曼曼司春棣张洪亮

重庆交通大学学报(自然科学版) 2021年11期

苏曼曼, 司春棣, 张洪亮

(1. 烟台大学土木工程学院, 山东烟台 264005; 2. 石家庄铁道大学交通运输学院, 河北石家庄 050010; 3. 长安大学特殊地区公路工程教育部重点实验室, 陕西西安 710064)

0 引言

为延长沥青道路的使用寿命并减缓沥青病害的发生，改性沥青在高速公路建设中被广泛使用。纳米材料拥有颗粒粒径较小、比表面积大等特性，能改变共混材料的微观结构。因此，纳米材料改性沥青受到越来越多道路研究者的关注[1-2]。G.SHAFABAKHSH等[3]、D.WANG等[4]研究了纳米TiO2对AH-70基质沥青的影响，研究结果表明，纳米TiO2增大了沥青的软化点，并提高沥青的高温抗车辙能力，同时纳米TiO2具有较好的耐光氧化能力，可提高沥青的抗氧化和抗老化能力；XU Xu等[5]对纳米ZnO热拌沥青混合料进行了室内试验研究，研究表明，纳米ZnO可改善沥青的抗老化及抗疲劳性能；H.Y.LIU等[6]则通过室内试验验证了经过表面修饰后的纳米ZnO能均匀分散于沥青中，并提高了沥青的抗老化性能；ZHANG Hongliang等[7]则通过纳米ZnO改性沥青的三大指标试验及老化试验等，验证了纳米ZnO能有效改善沥青的抗老化性能，并通过红外光谱试验验证了纳米ZnO与沥青之间发生了化学反应。

随着对纳米改性沥青研究的不断深入，越来越多的学者从不同角度采用不同的手段对纳米改性沥青的改性机理进行研究。ZHU Juncai等[8]、LI Rui等[9]分别通过原子力显微镜及扫描电镜试验观察纳米黏土、纳米ZnO在沥青中的微观结构，并通过对比基质沥青和改性沥青的微观形貌观察改性剂在沥青中的分散性；M.ABDELRAHMAN[10]通过红外光谱试验发现，纳米黏土与沥青之间产生了化学反应，打破了基质沥青的结构，同时具有较大比表面积的纳米颗粒与沥青之间产生较强的作用力，导致沥青具有较好的物理性能；张庆等[11]提出，可以通过差式扫描量热法研究橡胶改性沥青在老化过程中的相态转变温度，采用热重分析技术分析改性沥青组分，揭示改性沥青的改性机理；陈渊召等[12]采用组分分离试验分析了纳米ZnO改性沥青的改性机理，试验表明，纳米ZnO加入沥青中后，沥青质处于胶束中心，增大了沥青质的含量，进而提高了沥青的高温性能。目前对纳米改性沥青的研究大多均停留在宏观试验层面，主要研究改性剂对沥青物理性能改善效果，对改性沥青的改性机理研究仅限于红外光谱和扫描电镜等表象试验。扫描电镜和荧光显微镜仅能通过影像图片研究改性剂在沥青中的分散形貌，但仅根据分散情况推测沥青形貌的改变及对沥青性能的影响。红外光谱可以判定改性剂与沥青之间是否出现新的官能团，是否发生化学反应，但不能测定沥青分子与改性剂之间的相互作用力。因此，红外光谱和扫描电镜试验结果并不能全面、深入解释改性剂对沥青性能的改善原因。

分子动力学作为研究材料性质、揭示材料力学行为机理的一种新途径，在很大程度上起到沟通微观机理与宏观力学特性的桥梁作用。近几年，越来越多的学者将分子动力学研究方法应用于改性沥青的研究中。WANG Peng 等[13]构建了沥青分子模型、碳纳米管分子模型并进行分子动力学模拟，采用键接能和非键接能表征了各分子体系中的相互作用；SU Manman等[14-15]采用分子动力学方法研究了SBS改性剂与沥青之间的相互作用及沥青物理性能改善效果，进而，对聚合物/纳米ZnO共混材料的物理性能及共混体系中沥青分子结构变化进行了分子力学计算。笔者在前述研究的基础上进一步探究纳米ZnO与沥青的相互作用，揭示纳米ZnO对沥青物理性能及分子结构的影响。

笔者以SK-70沥青为研究对象，采用MS软件构建沥青分子模型、纳米ZnO模型及纳米ZnO/沥青共混体系，对各体系进行分子动力学模拟，然后研究纳米ZnO分子与沥青之间的相互作用、纳米ZnO在基质沥青中的扩散、纳米ZnO对沥青物理性能及分子结构的影响，通过分子动力学模拟结果解释纳米ZnO改性沥青的改性机理。

1 计算参数

1.1 相互作用能

采用分子间的非键接、范德华和静电相互作用能作为各体系稳定性的评价指标。以a、b两体系为例，相互作用能计算公式如式(1)～式(3)[16]：

En=Eabn-Ean-Ebn

(1)

EV=EabV-EaV-EbV

(2)

Eε=Eabε-Eaε-Ebε

(3)

式中：En为a、b体系非键接相互作用能，kcal/mol；EV为a、b体系范德华相互作用能，kcal/mol；Eε为a、b体系静电相互作用能，kcal/mol；Eabn、Ean、Ebn分别为ab共混体系、a体系、b体系的非键接能，kcal/mol；EabV、EaV、EVb分别为ab共混体系、a体系、b体系的范德华势能，kcal/mol；Eabε、Eaε、Ebε分别为ab共混体系、a体系、b体系的静电势能，kcal/mol。

1.2 扩散系数

纳米材料在沥青中的分散、迁移能力采用扩散系数进行表征，计算公式如式(4)[17]：

(4)

式中：D为扩散系数；t为时间，ps；r(t)为t时刻分子的坐标；s(t)为分子均方位移，Å2；m为均方位移随时间变化曲线的斜率。

1.3 物理模量参数

在分子模拟计算中，任一受到外力作用的体系均处于应力状态下，会引起体系内粒子相对位置的改变。对于各向同性的材料，其应力应变行为仅由拉梅常数便可完全描述，此时体系的刚度矩阵[c]则可通过拉梅常数建立其与应力应变之间的关系式，进而可计算各体系的体积模量K、剪切模量G，如式(5)～(10)：

(5)

(6)

(7)

(8)

(9)

(10)

式中：KH为Voigt-Reuss-Hill法体积模量近似均值；KV为Voigt-Reuss-Hill法体积模量近似上限值；KR为Voigt-Reuss-Hill法体积模量近似下限值；cij(i=1,2,…,6；j=1,2,…,6)为刚度矩阵中的分量值；Sij(i=1,2,…,6；j=1,2,…,6)为柔度矩阵分量值；GH为Hill法剪切模量近似均值；GV为Voigt法剪切模量近似上限值；GR为Reuss法剪切模量近似下限值。

1.4 结构参数

1.4.1 径向分布函数

径向分布函数反映分子间相互作用的本质，可用于分析共混体系微观结构[18]，其表征公式如式(11)：

(11)

式中：NAB为体系中A、B原子的个数；ΔNAB为对于A原子或者B原子，在r～r+δr范围内出现B原子或者A原子的个数；K为时步，ps；δr为间隔宽度，Å；ρAB为体系密度，g/cm3。

1.4.2 回转半径

回转半径能够反映分子体积与形状的动态变化规律，可用于评价分子体系的紧密程度和状态[19]，其计算公式如式(12)：

(12)

式中：Rg为回转半径；ri为分子质心到第i个链单元的距离；mi为第i个链单元的分子质量。

2 模型构建与模拟方法

2.1 沥青分子模型

SK-70基质沥青广泛应用于中国沥青路面，其基本性能参数如表1。

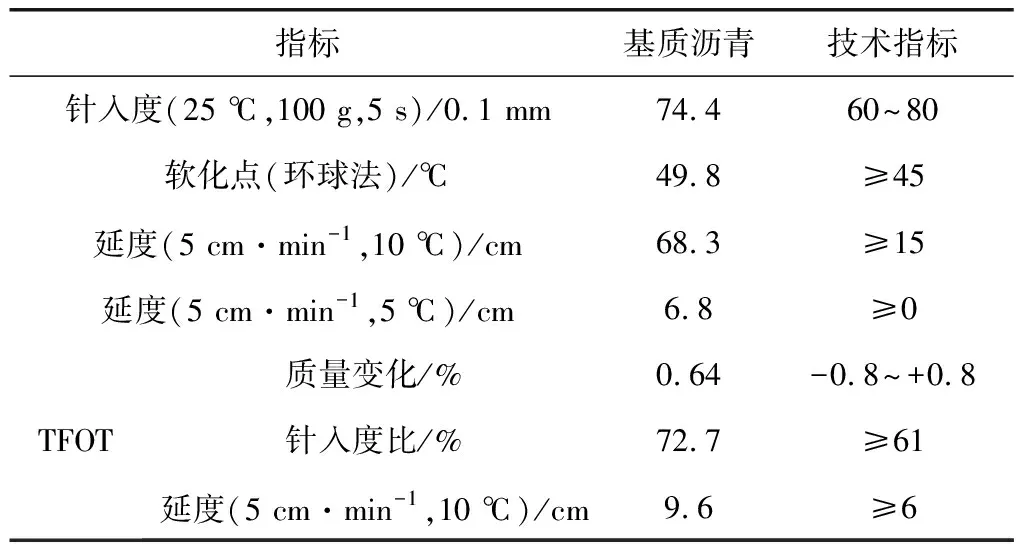
表1 SK-70基质沥青基本性能Table 1 Basic properties of SK-70 matrix asphalt

目前，沥青分子建模的方法有2种：一种为平均分子法，采用核磁共振、红外光谱等技术获取沥青的平均分子结构并建立沥青分子模型，此种方法无法获得沥青中不同组分化合物与其他物质的相互作用；另一种为组装法，可选定代表性分子代表沥青各组分，进而组装成沥青分子模型，组装法可更好地了解组分与其他物质的相互作用。笔者采用组装法构建沥青分子模型。

2.1.1 代表性分子

参照现有研究成果，选择沥青四组分代表性分子(图1)，其中：图1(a)～(c)为沥青质分子模型；图1(d)～(h)为胶质分子模型；图1(i)～(k)为芳香分分子模型；图1(l)～(m)为饱和分分子模型[20-25]。

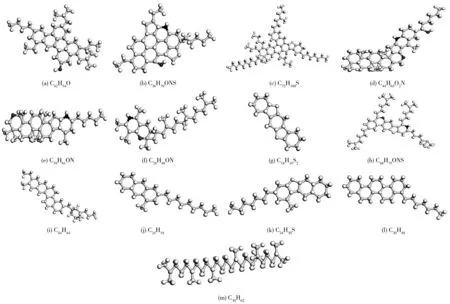
图1 沥青各组分代表性化合物Fig. 1 Representative compounds of asphalt components

2.1.2 沥青分子模型组装与验证

SK-70沥青分子模型组成如下：沥青质代表性分子a～c的分子个数分别为2、2、1；胶质代表性分子d～h的分子个数分别为3、6、6、4、9；芳香分代表性分子i～k的分子个数分别为10、16、15；饱和分代表性分子l～m的分子个数分别为10、13。各组分与元素含量的计算值与实验值如表2。显然，沥青分子模型各组分与各元素含量的计算值与实验值均较为接近。

表2 沥青组分相对含量及元素试验值与计算值对比Table 2 Comparison between test and calculated values of relative content of asphalt components and elements

2.2 纳米ZnO簇团模型

根据表3中纳米ZnO的晶格常数及空间群号构建纳米ZnO簇团模型(图2)，簇团直径分别设为4、6、8、10 Å。

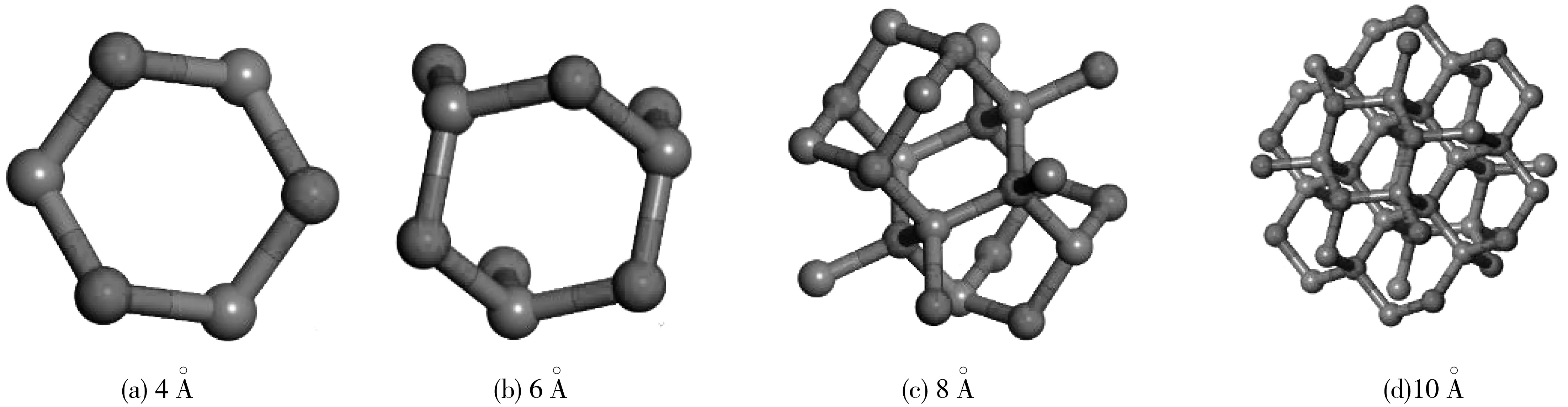
图2 不同粒径纳米ZnO簇团模型Fig. 2 Nano-ZnO cluster model with different particle sizes

表3 纳米ZnO晶格常数及坐标[26]Table 3 Lattice constants and coordinates of ZnO

2.3 共混体系模型

采用MS软件的Amorphous模块构建ZnO/沥青共混体系模型，各共混体系组成信息如表4，其中粒径为6 Å的ZnO/沥青混体系三维模型如图3。

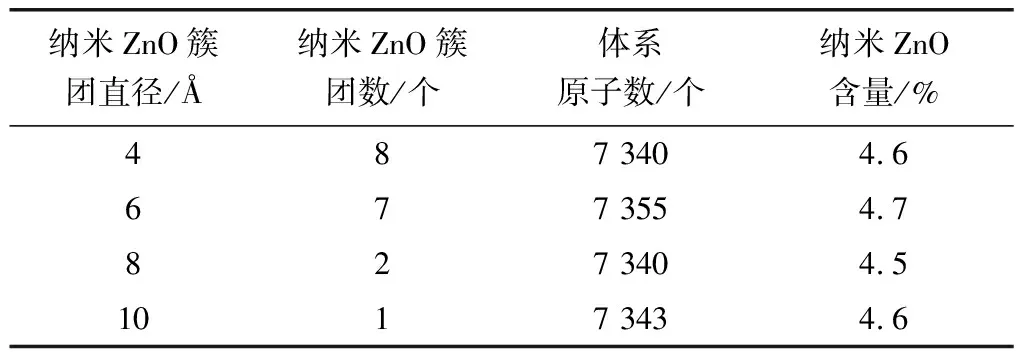
表4 各体系组成信息Table 4 Composition information of each system

图3 纳米ZnO/沥青共混体系Fig. 3 Nano-ZnO/asphalt blends system

2.4 模拟方法

笔者主要研究了纳米ZnO与沥青分子间的相互作用、纳米ZnO在沥青中的扩散、纳米ZnO对沥青分子结构及性能的影响等，分子模拟时选用力场为COMPASS力场，系综为等温等压系综，具体模拟过程如下：

1)首先，运用Focite模块对各体系进行能量优化和几何结构优化。

2)然后，进行退火处理，退火过程采用Amorphous模块的Protocols程序，温度为200～450 K，间隔为50 K。

3)体系结构稳定后利用Focite模块进行分子动力学模拟，体系分子动力学计算前后对比见图4。显然，分子动力学模拟后沥青四组分的排布基本符合胶体模型，即以沥青质为核心、胶质包裹着沥青质，随后是芳香分和饱和分，纳米ZnO则填充与沥青分子间隙。

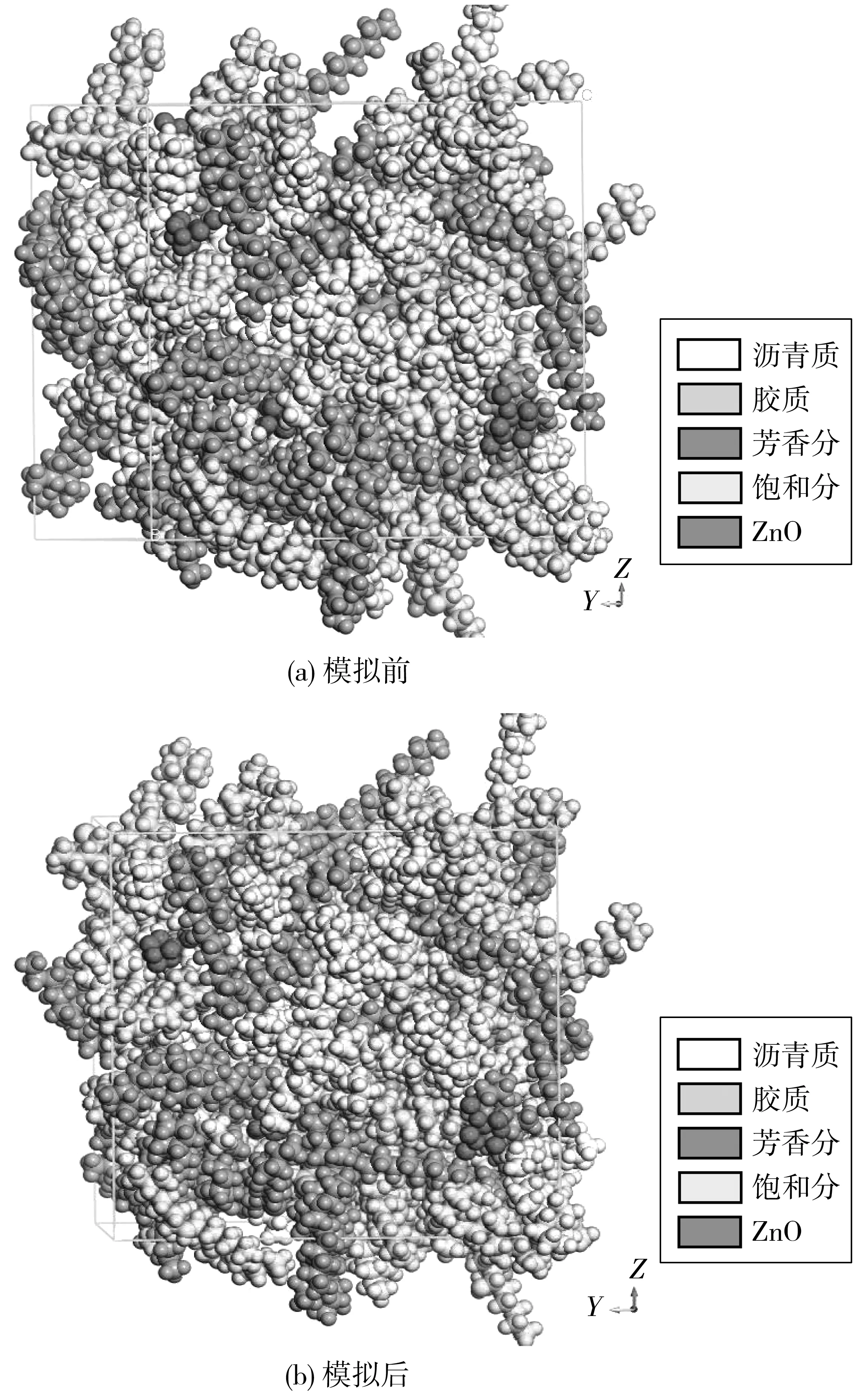
图4 ZnO/沥青共混体系分子动力学模拟前后对比Fig. 4 Comparison before and after molecular dynamics simulation of ZnO/asphalt blend system

4)对完成分子动力学计算的体系进行模拟，并计算物理性能、均方位移、回转半径等参数。

3 结果与讨论

3.1 ZnO对共混体系相互作用能的影响

图5为各共混体系在不同温度下的非键接相互作用能、范德华相互作用能和静电相互作用能模拟计算结果。显然，对任一共混体系，静电相互作用能几乎不受温度的影响，但范德华、非键接相互作用能则随温度的增长变化较大。对粒径为4、6 Å纳米ZnO/沥青体系，模拟计算温度小于410 K时，范德华相互作用能和非键接相互作用能随温度的增长波动较小；温度大于410 K时，二者随温度的增长波动较为剧烈。簇团粒径为8 Å时，共混体系范德华相互作用能和非键接相互作用能随温度的波动幅度最大。簇团粒径为4、6、8、10 Å的纳米/沥青共混体系的范德华相互作用能和非键接相互作用能绝对值分别在温度为423.3、422.5、418.3、423.2 K时达到最大。可见，粒径对纳米ZnO/沥青体系结构最稳定对应的温度影响不大，约在150 ℃时各体系分子间相互作用能最大。通常，分子间相互作用能越大，分子结构越稳定，从热力学观点可以认为，当纳米ZnO/沥青体系结构破坏时需要更多的能量，可以理解为加入ZnO后沥青结构体系变得更稳定了。

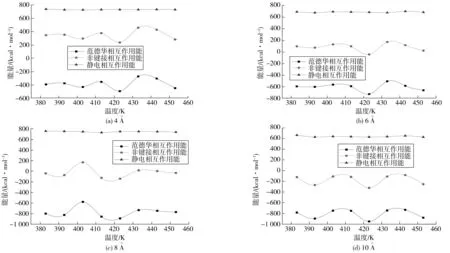
图5 不同粒径纳米ZnO/沥青体系相互作用能随温度的变化Fig. 5 Variation of interaction between nano-ZnO with different particle sizes chaning with temperature

3.2 ZnO粒径对扩散系数的影响

图6为不同纳米粒径ZnO在沥青中时间-均方位移的变化规律。

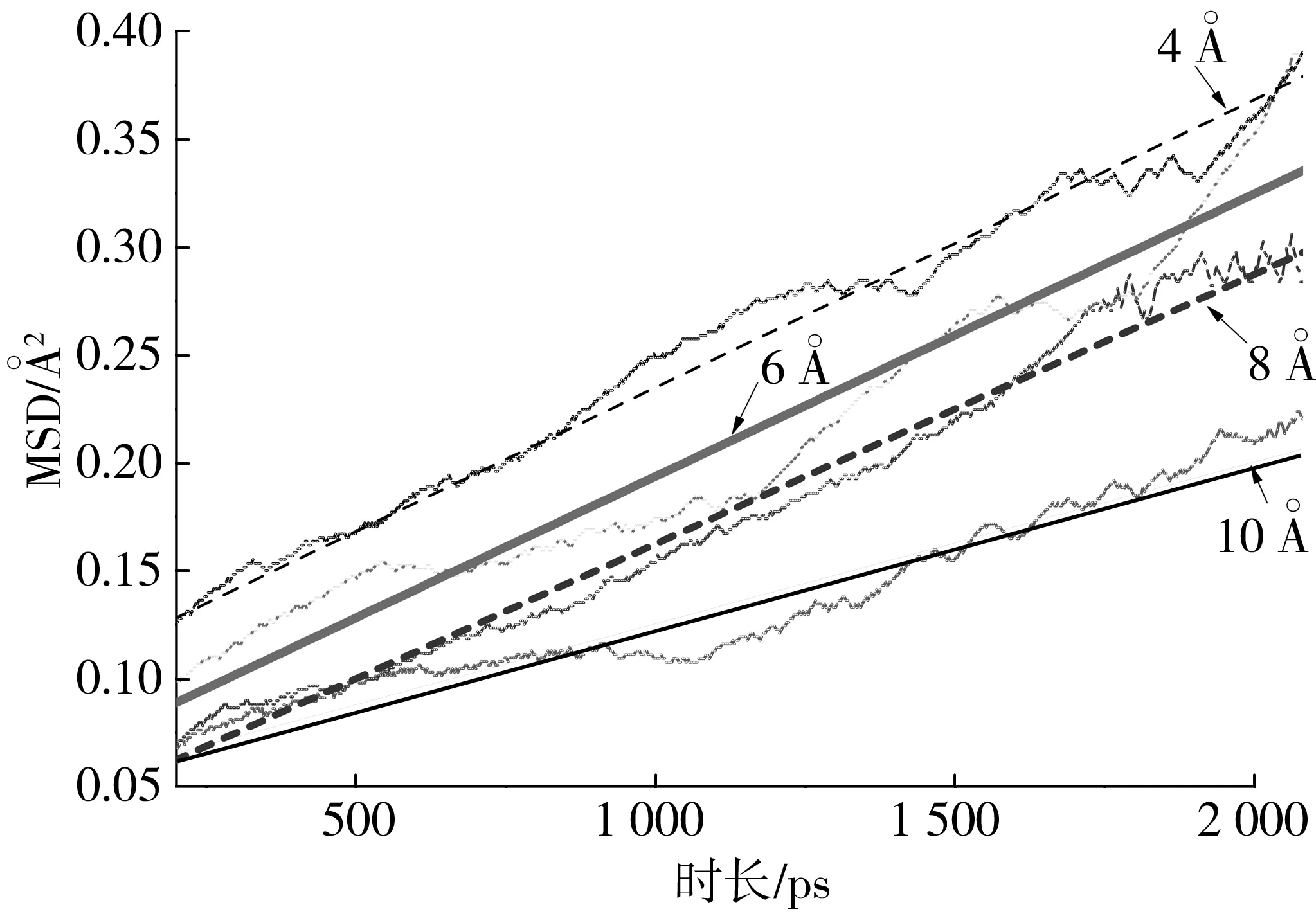
图6 ZnO粒径均方位移随模拟时间的变化Fig. 6 Variation of mean square displacement of nano-ZnO particle size changing with simulation time

由图6可知，不同纳米粒径ZnO/沥青体系中纳米ZnO均方位移随模拟时间的延长逐渐增大，且纳米ZnO粒径对纳米ZnO均方位移有一定影响。

对各曲线进行一次线性拟合的拟合方程见表5。根据式(4)可计算粒径为4、6、8、10 Å时纳米ZnO在沥青中的扩散系数，分别为0.336 8×10-4、0.328 4×10-4、0.293 1×10-4、0.258 0×10-4。粒径为6、8、10 Å纳米ZnO簇团在沥青中的扩散系数分别比粒径为4 Å纳米ZnO在沥青中的扩散系数降低了2.5%、12.9%和23.4%。可见，随着纳米ZnO粒径的增大，纳米ZnO粒子在沥青中的扩散能力减弱。因此，仅从纳米颗粒扩散能力角度考虑，在实际工程中应选取粒径较小的纳米材料。

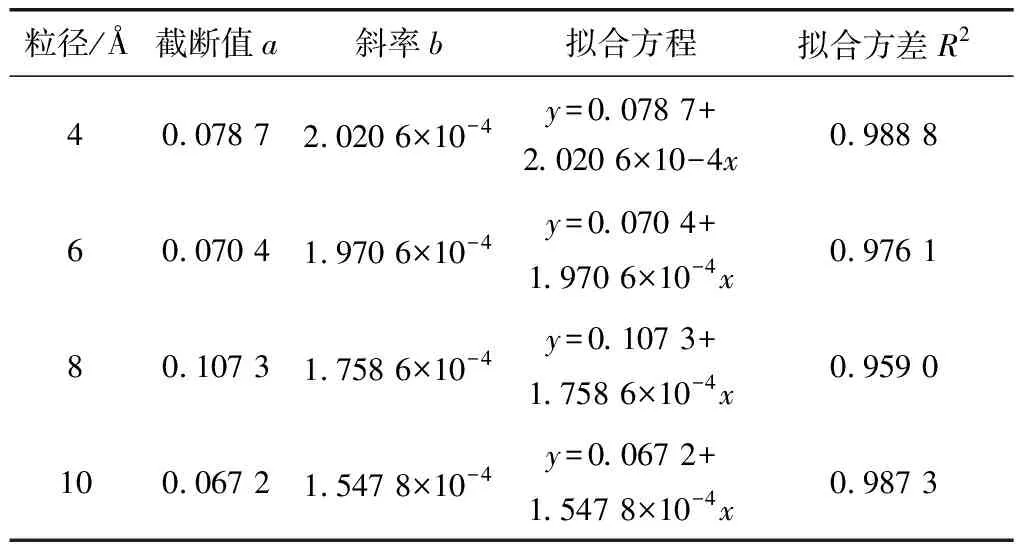
表5 不同粒径ZnO均方位移拟合式Table 5 MSD formula of nano-ZnO with different particle size

3.3 ZnO对沥青物理模量的影响

图7为各共混体系剪切模量、体积模量和弹性模量的模拟计算结果。向沥青体系中加入纳米ZnO颗粒后，沥青的弹性模量(E)、体积模量(K)和剪切模量(G)均发生了改变。4、6、8、10 Å纳米ZnO/沥青体系的弹性模量比基质沥青体系的弹性模量分别增长了2.03%、6.27%、6.5%和5.85%；体积模量则较沥青体系分别增长了15.09%、12.46%、10.06%和8.51%；剪切模量较沥青体系分别增长了1.33%、1.71%、5.33%和2.21%。可见，粒径大于4 Å后的纳米ZnO对弹性模量的影响较小；粒径为8 Å时，弹性模量增长幅度最大，此时剪切模量增长幅度亦达到最大。纳米ZnO对沥青物理性能的改善原因在于纳米ZnO颗粒粒径较小，可以在沥青分子孔隙中穿越，在一定程度上起到了填充作用，增大了沥青的体积模量。同时，也在一定程度上提高了沥青的剪切模量和弹性模量。而剪切模量的提升则意味着沥青在高温下的抗剪能力得到提升，从而改善了沥青的高温性能。该模拟计算结论与室内试验结果一致[7]。

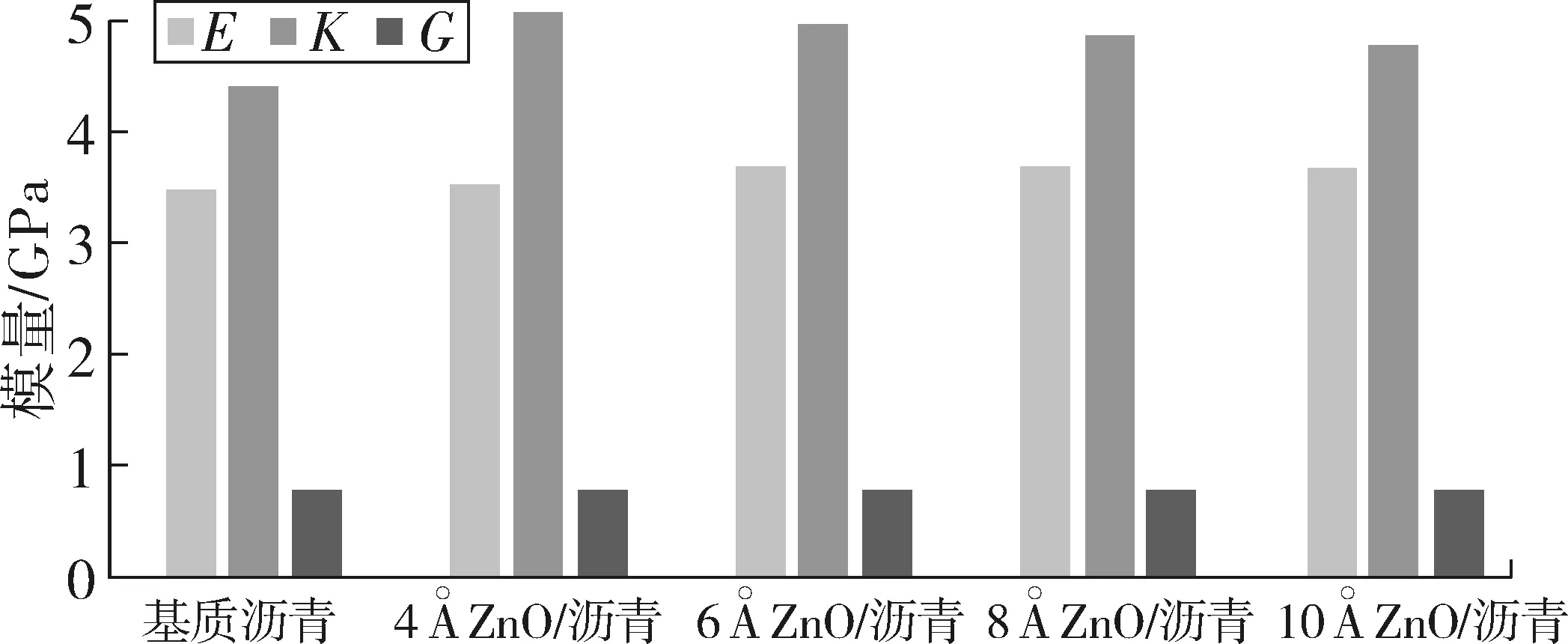
图7 沥青体系与共混体系力学参数Fig. 7 Mechanical parameters of asphalt system and blend system

3.4 ZnO对沥青分子结构的影响

取粒径为8 Å的ZnO簇团与沥青分子构建共混体系，研究ZnO对沥青分子结构的影响。

3.4.1 ZnO对沥青各组分芳环质心径向分布函数的影响

图8为纳米ZnO对沥青各组分芳环质心径向分布函数分子动力学模拟结果。不同体系的g(r)随着原子间距的增加均趋近于1，此为典型的非晶结构特点。未加入ZnO时，沥青质、胶质、芳香分和饱和分体系出现第一个峰值的位置分别为1.08、1.12、1.11、1.08 Å；加入ZnO后，沥青质和胶质体系第一个峰位置分别右移了0.02、0.03 Å，饱和分体系出现第一个峰值的位置则左移了0.07 Å，芳香分体系第一峰的位置未改变。未加入纳米ZnO簇团时，沥青质、胶质、芳香分和饱和分体系的首个峰值分别为41.61、29.03、24.18和41.71；加入纳米ZnO后，各体系峰值分别改变为65.77、56.51、45.77和57.23，提高量分别为34%、49%、48%和37%。峰值强度提高说明芳环在该范围内堆积密度提高，而且各体系径向分布函数在不同位置的峰值均呈现出高而尖的特点，这表明分子的有序性增强，原子之间联系较为紧密。

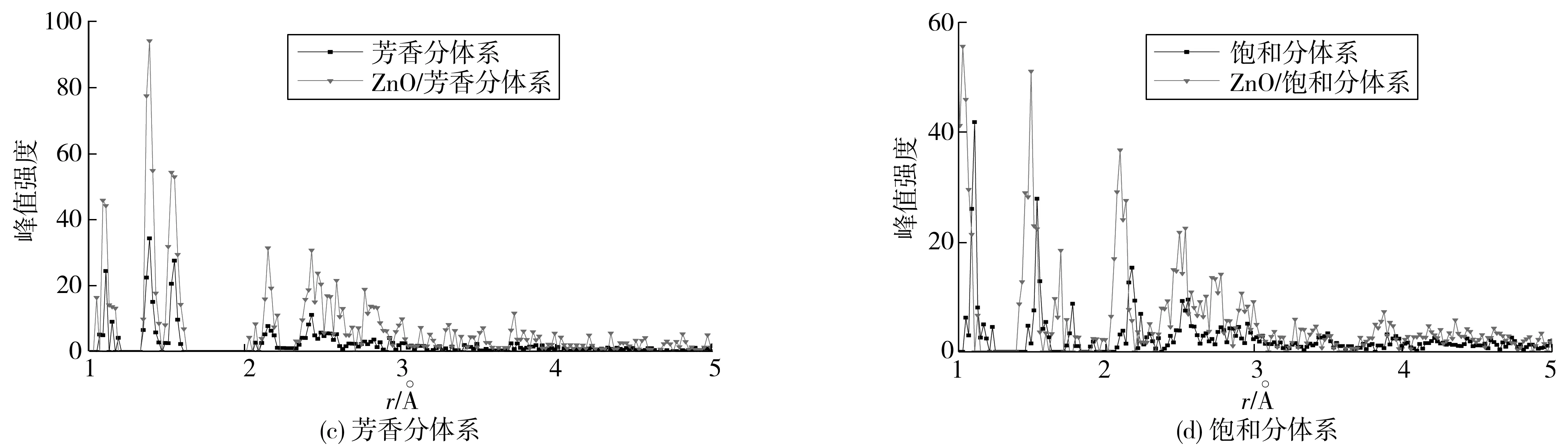
图8 各组分在添加纳米ZnO前后的峰值强度比较Fig. 8 Peak intensity for asphalt components before and after adding nano-ZnO

3.4.2 ZnO对沥青各组分支链回转半径的影响

图9为加入纳米ZnO前后沥青各组分代表性分子支链回转半径变化情况。未加入纳米ZnO时，沥青质、胶质、芳香分分子侧链和饱和分回转半径值分别在4.32、5.31、5.75、4.81 Å处。加入纳米ZnO后，沥青质、饱和分、胶质和芳香分支链回转半径峰位分别左移了0.66、0.71、0.21、0.17 Å。未加入纳米ZnO时，沥青质、胶质、芳香分和饱和分分子支链回转半径峰宽为1.5、1.9、2.6、3.0 Å，加入纳米ZnO后，各组分支链回转半径峰宽则变为1.6、1.9、1.62、2.2 Å。可见，纳米ZnO对沥青质峰宽影响较小，对胶质峰宽没有影响，对芳香分和饱和分峰宽影响较大，二者峰宽分别减小了0.58、0.80 Å。各组分的回转半径可以反映其致密程度，回转半径峰值左移表明体系发生了塌缩，体系致密程度增大。峰宽越小则表明支链在空间的延展性越强，越容易包裹周围的分子。

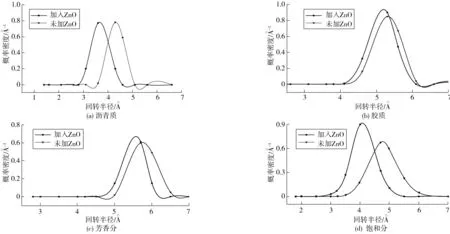
图9 不同组分分子支链回转半径计算结果Fig. 9 Calculation results of molecular branch chain radius of gyration of different components

由纳米ZnO对沥青分子结构影响的模拟结果可知，纳米ZnO增大了沥青质与胶质体系分子间的芳环质心距离，减缓了强极性组分的堆积，同时缩小了芳香分和饱和分分子间芳环质心的距离，加强了支链在分子间的延展性。可见，纳米ZnO从整体上加强了沥青各组分之间的交错，增加了沥青结构的致密性，促使沥青形成更稳定的胶体结构，从而提高了沥青的物理性能。