最小二乘叠前时间偏移在川东南复杂构造成像中的应用

袁茂林

（中国石化勘探分公司油气勘探管理部，四川成都 610041）

针对岩性油气藏、复合型油气藏以及隐蔽性油气藏等复杂的勘探目标，不仅要求构造成像精确，而且对岩性成像提出了更高的要求。地震偏移技术在实际生产中存在如下问题：陆上震源子波时空变化剧烈、有限的波场带宽、数据不规则及稀疏性等，这些客观因素往往会导致偏移结果的振幅保真度和成像分辨率较低，难以满足岩性解释的需求。理论上，在油气勘探领域被广泛应用的互相关成像算子仅仅是正演算子的共轭，而不是它的逆。因此，常规的地震偏移只能对地下构造进行模糊成像，往往提供欠估计的反射系数信息。本质上，偏移成像是地下反射系数经过Hessian 算子滤波后的结果。为了消除Hessian 算子对成像结果的模糊化影响，可以将地震成像看作最小二乘框架下的线性波形反演（最小二乘偏移，LSM）问题，在数据空间域估计出分辨率较高、振幅信息可靠的地下反射系数的像，从而有利于后续的AVA/AVO 反演、叠前反演以及岩性解释等工作。

Tarantola［1］早在1984年提出了基于最小二乘反演的地震成像思路。LeBras 和Clayton［2］、Lambare等［3］、Nemeth 等［4］以及Duquet 等［5］对最小二乘偏移技术进行了完善。但是，最小二乘偏移技术在工业界仍然没有得到广泛应用，影响其推广应用的因素主要有两个：一方面是计算效率较低，其计算工作量大约是常规地震偏移的N×2 倍（N是反演迭代的次数，次）［6-8］。另一方面，在实际资料处理中，子波问题、速度问题、资料信噪比问题、资料振幅一致性问题等等都会影响最小二乘偏移质量，尤其是实现最小二乘叠前深度偏移的难度非常大，主要原因如下：①陆地震源子波吸收衰减强，其时空变化剧烈，导致实际采集的地震记录与模拟的地震记录振幅匹配度较低［9］；②叠前深度偏移成像对速度模型的精度要求极高，高精度深度域速度模型建立已经成为深度域成像的最大难题［10］；③地震资料中存在的多种噪声、多次波等干扰不在数据匹配的理论框架内，成为LSM 方法迭代反演难以有效收敛甚至不收敛的阻碍因素［11］。

基于以上分析，将一对互为共轭数学关系的叠前时间偏移及反偏移算子引入到共轭梯度的最小二乘反演框架中，通过编写C 语言程序实现了最小二乘叠前时间偏移（LS-PSTM）技术。通过模型数据和实际资料处理验证了本文方法可以有效压制成像噪声、提高成像分辨率以及补偿常规偏移的成像振幅，在川东南复杂构造区具有良好的应用效果。

1 基本原理

在born 近似的线性化条件下，地震正演可以表达为如下矩阵的数学形式［12］：

其中，d为地震数据；m为地下的反射系数；L为叠前时间反偏移算子。

同样地，线性化地震正演的共轭算子也可以写成矩阵的数学形式：

此处，mmig表示反射系数的成像结果；LT为叠前时间偏移算子［13］。

将式（1）带入式（2），得到

从式（3）可以看出，mmig是地下反射系数m经过Hessian 算子LT L滤波后的模糊成像，为了消除Hessian 算子LT L对地震成像的影响，可以将地震成像看作最小二乘框架下的线性波形反演问题，其目标是反偏移数据d与地震数据d0之间的误差最小，从而最优化地估计出地下反射系数。定义如下目标误差泛函［14］：

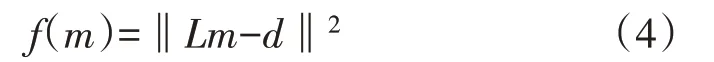
该泛函要求反演成像一定要使反偏移数据遵循地震数据的振幅变化规律，因此，数据预处理阶段需要对数据进行单炮能量一致性校正。

为了求解式（4）所示的目标误差泛函，可以采用共轭梯度类算法：

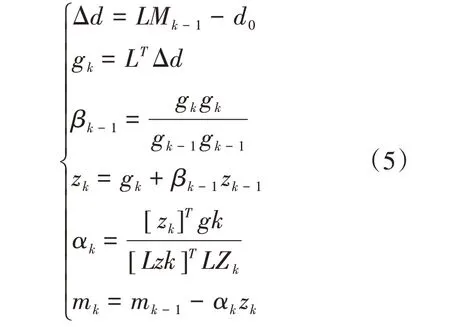
其中，Δd是数据残差；mk（m0=0）是第k次迭代的反演成像结果；gk是梯度；βk-1为更正因子；zk为共轭梯度；αk为迭代的步长。当数据残差减小到低于预设阈值时，迭代算法自动停止［15］。

LS-PSTM 技术流程如图1 所示，从流程图中可以看出，LS-PSTM 计算量为常规叠前时间偏移的N×2倍。

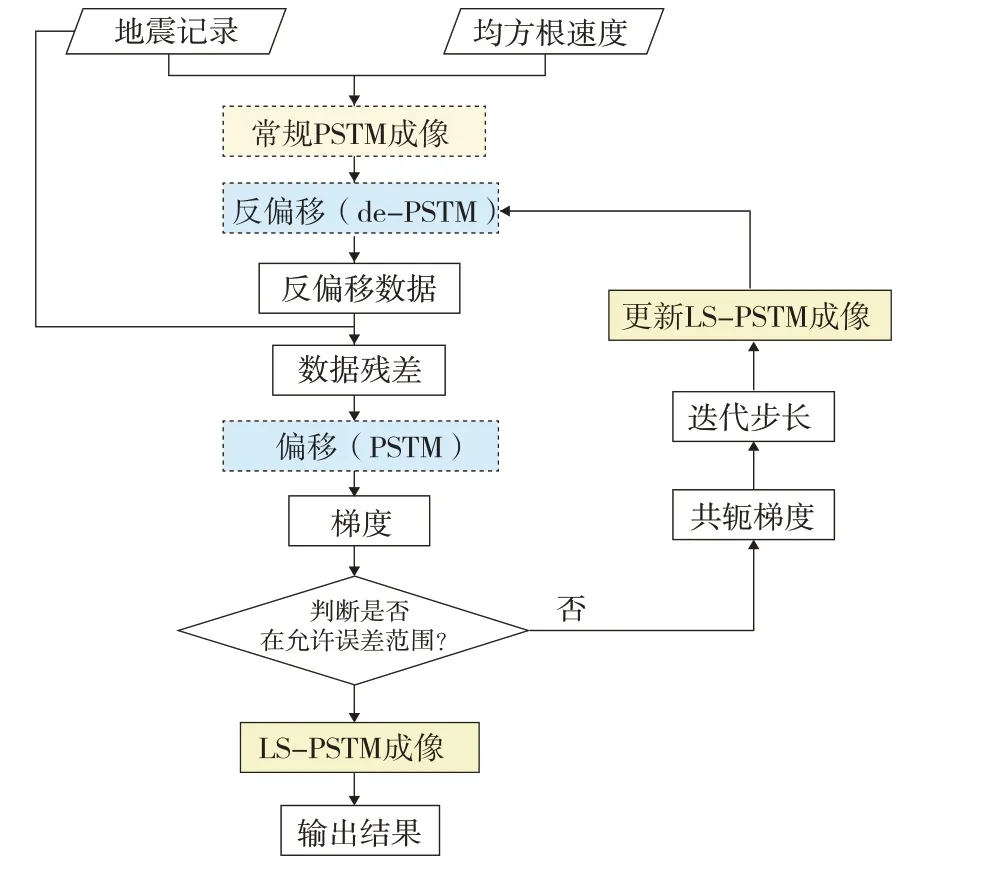
图1 最小二乘叠前时间偏移技术流程

2 测试与应用

2.1 缝洞体模型测试

为了验证本文发展的最小二乘叠前时间偏移技术的正确性、有效性和适应性，在编程实现LSPSTM算法的基础上，采用缝洞体模型进行测试。

图2a 为层速度模型，模型大小为1 000×2 001，纵横向间隔为5 m，可以看到在两个水平层下面有五个尺度大小不一的缝洞体，最小缝洞体尺度为5 m×5 m，缝洞体是异常低速度。图2b 为迭代反演使用的均方根速度场。

图2 速度模型

为了比较真实地模拟实际地震数据，采用波动方程高阶有限差分算子进行正演。地震数据总共350 炮，炮间隔10 m，每炮151 道接收，道间隔10 m，每道有2 001个采样点，采样率2 ms。图3是地震数据的单炮记录，可以看出，除了有效的反射波和绕射波之外，记录中还存在两组多次波，分别来自第二层反射界面和缝洞体。

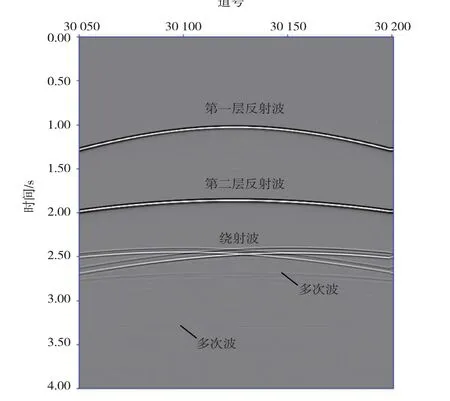
图3 地震单炮记录

根据式（5）所示的共轭梯度算法，采用上述模型和地震记录进行LS-PSTM，并且在实际计算过程中隔炮隔道对数据进行抽稀。图4a 和图4b 分别为常规PSTM结果和LS-PSTM结果。

图4 成像结果

可以看出，常规PSTM 成像分辨率较低，振幅不均衡，而且缝洞体成像能量聚焦性较差，且存在较严重的多次波成像和偏移噪声。LS-PSTM 成像分辨率更高，补偿了成像振幅，多次波和偏移噪声在一定程度上得以压制，缝洞体成像能量更加聚焦，缝洞体刻画更加清晰，这一特点同样可以延伸应用到断裂、高陡构造侧翼（传播距离大、衰减多）以及小尺度岩溶缝洞体成像中。

为了定量地分析成像分辨率与成像振幅，接下来计算常规PSTM 和LS-PSTM 结果的频谱。从图5可以看出，常规PSTM 结果缺少反射的高频成分，导致频谱带宽很窄，表明成像分辨率很低。此外，常规PSTM 成像振幅是欠估计的。相反，LS-PSTM 恢复了反射系数的高波数成分，拓宽了频带，并且没有损失有效的低频信息，表明LS-PSTM 能够提高成像分辨率。而且，LS-PSTM 有效地补偿了成像振幅，达到保幅成像的目的。

图5 频谱

收敛曲线是检验LS-PSTM 的有效指标。图6是15 次迭代的反演收敛率曲线，可以看出，在最初的几次迭代中，数据残差降低得很快，接着收敛速度开始减慢，并且保持继续降低的趋势。然而，由于地震数据中存在严重的多次波干扰，导致迭代收敛速度明显减慢。

图6 收敛曲线：数据残差经过归一化处理

2.2 川东南实际资料应用

为了分析验证本文发展的最小二乘叠前时间偏移技术在实际生产中的应用效果，针对川东南岩溶缝洞储层及高陡构造页岩气勘探，开展了实际地震资料处理。

2.2.1 岩溶缝洞体成像

川东南茅口组发育规模断层岩溶缝洞体，油气高产富集条件优越，是实现少井带动高效勘探的有利目标。但是，实际地震资料目的层分辨率较低、振幅能量相对较弱，岩溶缝洞异常识别困难。

图7a 是川东南实际资料常规PSTM 结果，图7b是川东南实际资料LS-PSTM 结果。从图7a 可以看出，常规PSTM 成像分辨率较低，振幅保真度较低，无法识别二叠系反射层（Tp2）茅口组岩溶缝洞储层。从图7b可以看出，LS-PSTM不仅提高了茅口组成像分辨率，突出了岩溶缝洞异常，岩溶缝洞体成像更加清晰，而且补偿了成像振幅，保持了常规PSTM结果的波组特征和振幅强弱相对关系，层间信息更加丰富，能够有效地支持岩溶缝洞地质评价工作。

图7 川东南实际资料地震成像

为了定量地分析成像分辨率与成像振幅，接下来计算常规PSTM 和LS-PSTM 结果的频谱。从图8可以看出，PSTM 结果的主频为26 Hz，缺少反射系数的高频成分，导致频谱带宽很窄，表明成像分辨率很低。相反，LS-PSTM 恢复了地下反射系数的高频成分，且没有损失低频成分，拓宽了频带，并且地震资料的主频提高至31 Hz，表明LS-PSTM 能够提高成像分辨率。

图8 频谱对比

图9 是20 次迭代反演的收敛率曲线，收敛曲线是检验LS-PSTM 稳定性的有效指标。从图9 可以看出，在最初的几次迭代中，数据残差降低得较快，接着收敛速度开始减慢，并且保持继续降低的趋势，说明LS-PSTM过程是稳定且收敛的。

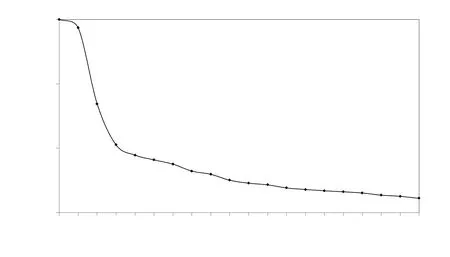
图9 收敛曲线：数据残差经过归一化处理

2.2.2 高陡构造成像

川东南高陡构造钻井、野外露头显示，高陡构造主体具有较好的页岩气勘探潜力。但是，由于受多期构造运动的影响，构造变化剧烈，地层倾角变化大，地层速度纵横向变化快，地震波场极其复杂，地震成像困难。

图10 是川东南高陡构造成像处理结果，图10a是商业软件常规PSTM 结果，图10b 是LS-PSTM 结果。对比可以看出，LS-PSTM 压制了偏移噪声，改善了高陡构造成像质量，高陡构造内幕波组特征更加清晰，断背斜顶部成像较完整，有利于志留系（Ts）页岩气保存条件评价工作。此外，向斜区Ts 反射层波组连续性好,断层位置更加明确，基底断裂成像分辨率更高（图中黑色虚线方框所示），有利于二叠系茅口组储层评价工作。

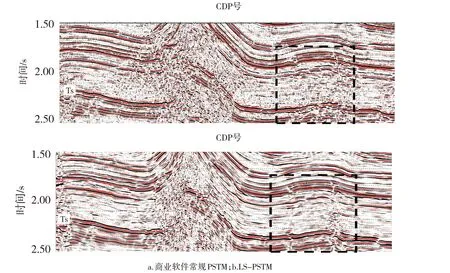
图10 川东南实际资料地震成像

3 结论与认识

将地震成像看作最小二乘框架的反演成像问题，构建了互为共轭关系的偏移/反偏移算子，利用共轭梯度法进行最小二乘叠前时间偏移（LSPSTM），在数据空间域计算出分辨率较高、振幅信息可靠的地下反射系数的像。通过缝洞体模型数据测试验证了LS-PSTM 技术的正确性和有效性，相比于常规PSTM，更能够提高成像信噪比、成像分辨率以及振幅保真度。

将LS-PSTM 技术应用于川东南实际资料处理中，取得良好的应用效果。①LS-PSTM 提高了二叠系茅口组成像分辨率，突出了岩溶缝洞异常；②LSPSTM 改善了高陡构造成像质量以及向斜区志留系反射层波组连续性，并且提高了向斜区基底断裂成像分辨率。

随着勘探目标日趋复杂，实际生产对地震成像精度的要求越来越高。LS-PSTM 技术展现了解决复杂构造成像难题的能力，伴随计算机运算能力不断提升，LS-PSTM 技术具有良好的推广应用前景。