基于中性等效风速的海上风廓线建模方法研究
2021-12-17刘永前马晓梅高小力
刘永前, 马晓梅,2, 高小力, 阎 洁, 韩 爽
(1.华北电力大学 新能源电力系统国家重点实验室, 北京 102206; 2.青海师范大学 物理与电子信息工程学院 青海 西宁 810016)
0 引 言
海上风资源储量丰富稳定且靠近负荷中心[1],能够有效缓解目前资源和环境危机,相比于陆上风电,还能减少视觉和噪声影响[2];除此之外,由于海上风切变较低,风电机组轮毂高度即使低于陆上也可以带来较好的经济效益。因此,海上风电成为近年来的发展热点。海上风资源评估是海上风电场开发建设的基础[3],但是由于海上风资源气象属性复杂,海上测风资料相对缺乏,加之评估技术还处于初级研发阶段[4],可行性论证难度较大。因此,提高海上风资源评估的准确性是降低海上风电项目投资风险,提高核心竞争力的关键。
海上风资源评估最重要的基本要素是测风资料,由于海上长期、准确的观测数据相对缺乏,海上风资源评估一般采用有限的陆上测站数据、浮标数据、卫星数据或再分析数据。其中,再分析数据由于渠道多、获取方便而被广泛使用。Sheridan L M等利用再分析数据表征海上风资源的不确定性,指出再分析数据与观测数据存在一定偏差[5]。Chancham等人利用再分析数据评估了泰国湾的海上风资源并提出了海上风电场优化设计方案[6]。Zheng Chongwei 等人利用欧洲天气预报中心再分析数据重新评估了全球海上风能资源[7]。但是再分析数据往往不能满足海上风电机组轮毂高度要求,需采用外推的方式评估轮毂高度风资源,而目前普遍采用的外推方式忽略了大气稳定度、海面动力学粗糙度等影响,加之再分析数据本身与观测数据就有误差,将可能导致不合理的风资源评估结果。
海上大气边界层下垫面是变化复杂的海面,研究海洋表面状况参数化模型有助于深入认识海上大气边界层物理过程,从而提高海上风资源评估精度。Charnock[8]和Smith[9]最早提出了海洋表面粗糙度参数化模型,建立了摩擦速度和粗糙度之间的线性模型。文献[10]研究了不同海面动力学粗糙度参数化模型对风、温等气象要素垂直廓线数值模拟的影响。大气稳定度也是影响海上风资源分布的重要因素。文献[11]研究了大气稳定度对风资源时空分布的影响,文献[12]分析比较了不同大气稳定度分类标准对沿海地带风切变指数计算的适用性,得到风切变指数与大气稳定性存在高度相关性的结论。文献[13]通过风电场精细化建模得到大气稳定度对风电场功率输出有较大影响。文献[14]利用测风塔观测资料分析了渤海湾北岸湍流强度特征,提出了调整风电机组抗湍流参数的建议。但是,上述文献在研究海上风资源特性时,都采用单一参数描述,且部分研究直接用海面动力学粗糙度参数化模型拟合海上风廓线,忽略了模型中大气始终处于中性层结的假设。
实际上,海洋表面状态时刻都在变化,且大气出现中性层结的时段很少,这种近似方式将带来风资源评估误差,导致整场发电量设计值与实际运行值的偏差[15]。本文采用海上测风塔实际测风数据,引入中性等效风速,将处于稳定及不稳定状态的风速转化等效于中性状态的风速,再结合莫宁奥布霍夫相似理论和海洋表面动力学粗糙度参数化模型来描述海上风资源的垂直分布,为提升海上风资源评估精度、降低海上风电项目的投资风险提供依据。
1 海上风资源评估参数及模型研究
1.1 大气稳定度参数模型
莫宁奥布霍夫长度(以下称莫奥长度)L和梯度理查森数Ri都是表征大气稳定度状态的稳定度参数,用实际观测得到的离散资料计算梯度理查森数时,用如下计算方法[16]:
(1)
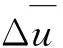
莫奥长度和梯度理查森数的关系如下:
(2)
1.2 摩擦速度参数化模型
研究海洋与大气的相互作用时,基于雷诺应力关系,利用 10 m 高度处平均风速U10及其对应的拖曳系数Cd可得到摩擦速度计算式[17,18]:
(3)
拖曳系数决定了大气与海洋之间的动量传输率,随风速的变化而变化,并与海面粗糙度和大气稳定度有关[19]。本文考虑的拖曳系数参数化模型为Largeand Pond模型:
(4)
1.3 海洋表面动力学粗糙度参数化模型
Charnock[8]最早提出了海面粗糙度与摩擦风速的关系:
(5)
式中:α=0.018 5,Charnock方案被广泛地应用,之后的参数化方案研究基本都是在此基础上进行的,Smith[9]在Charnock模型基础上加入了海面光滑流的影响:
(6)
Charnock参数化模型能较好的模拟海上边界层物理过程,因此本文采用Charnock模型。
1.4 不同稳定度下的风廓线模型
由莫宁-奥布霍夫相似理论得到近地面层风速的通量—廓线关系的积分形式为
(7)
式中:ψm是风廓线稳定度修正函数;z0为海洋表面动力学粗糙度;u*为摩擦速度;k为冯卡门系数,取0.4:
(8)

2 基于中性等效风速的海上风廓线模型
现有海面动力学粗糙度参数化模型及风资源评估软件等考虑到建模难度、计算速度等限制,均假设大气始终为中性状态,在一定程度上限制了评估精度的进一步提升。目前风电机组轮毂高度已经超过了160 m,当轮毂高度超出测风高度时,需要将测风高度的风速外推到轮毂高度。为了满足某些模型及评估软件对大气状态的假设,本文提出基于中性等效风速的海上风廓线模型。
2.1 基于中性等效风速的海上风廓线模型
假设uzn为满足中性条件的高度z处的风速,则有
(9)
联立式(7)和(9),得
(10)
式中:u(z)为测风高度z处任意时刻的实测风速;ψm为该时刻对应的稳定度函数。
考虑到计算方便及数据可利用性,本文先用两个高度层逐时刻的风速、温度数据计算梯度理查森数及莫奥长度,判断大气稳定度分类并将逐时刻ψm代入式(10),将逐时刻风速转化为中性状态下的等效风速,该等效风速对逐时刻的大气状态进行了中性等效转化,可以满足某些模型及评估软件对大气状态的假设。
假设u1n为高度z1对应的中性状态等效风速,z2,u2分别为需要外推的轮毂高度及风速,由于低层风速已经做了等效转化,因此本文外推时用中性状态下的对数率,即
(11)
代入式(10),得
(12)
式中:z0采用Charnock模型,即
(13)
式(13)为基于中性等效风速的海上风廓线模型。由于高度z1处的风速采用的是中性等效风速,大气状态及海面动力学粗糙度等已经作为低层的考虑因子,因此外推得到的u2即为高度z2处接近于实际状态的风速。相比于直接用低层风速和对数率外推轮毂高度风速的方法,模型综合考虑大气稳定度和海面动力学粗糙度对海上风廓线的影响,其结果更能接近实际情况,减少由于外推带来的计算误差。图1为基于中性等效风速的海上风廓线模型流程图。

图1 模型流程图Fig. 1 Flow chart of proposed model
2.2 模型评价指标
在实际应用中,均方根误差RMSE和平均绝对误差MAE可以用来衡量预测值与真值之间的偏差,因此,本算例采用这两个指标来评价模型的精确度,计算公式如下:
(14)
(15)
3 算例分析
3.1 海上测风塔信息
本文以大连庄园某海上风电场测风塔数据为1号风电场数据,江苏某海上风电场测风数据为2号风电场数据,首先利用1号风电场数据进行海上风资源分布分析,再利用1号和2号海上风电场数据验证本文提出的基于中性等效风速的海上风廓线模型。1号测风塔位于黄海北部大南岛附近海域;数据采集时间为2016年1月1日0时~2016年12月31日23时50分,采样周期为10 min。原始数据完整率较高,达到95%以上,根据国家标准GB/T18710-2002及行业标准NB/T 31147-2018,经数据插补后完整率为100%;2号测风塔数据采集时间为2017年1月1日0时~2017年12月31日23时45分,采样周期为15 min,经数据插补后完整率为93%,表1为1号和2号测风塔基本信息。

表1 测风塔基本信息Tab.1 Information of wind mast
3.2 海上风资源分布
3.2.1 大气稳定度参数及分类
大气稳定度是造成风速垂直变化的主要热力因素。根据式(1)、(2)计算逐时刻梯度理查森数及莫奥长度,利用表2的分类标准将大气状态进行分类。

表2 大气稳定度分类标准Tab.2 Standard of atmospheric stability classification
为了验证大气稳定度分类的准确性,保证外推计算的精度,统计了1号风电场大气状态分类情况。图2是大气稳定度逐时刻的分类情况,图3是不同季节大气稳定度的分类情况。可以看出,无论是什么时间尺度,中性状态的比例都不高,在图1中,中午时刻不稳定占的比例高于其他时刻,夜里稳定时刻所占的比例更高,综合来看,全年大气处于不稳定状态比例更多。
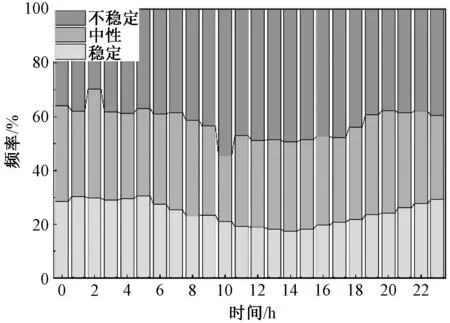
图2 逐时刻大气稳定度分类 Fig. 2 Classification of atmospheric stability by hour
一般情况下近地层中气温随高度的升高而降低,而气温随高度的升高而升高的现象称为逆温。当陆地较暖的空气平流至较冷的海面时,海面上就可能形成逆温层。逆温层的存在阻止气流的垂直运动,使大气处于稳定状态,且逆温层越厚,影响就越大。在图3中,春季稳定状态所占的比例明显高于其他季节,分析其成因,计算统计了出现逆温现象的时刻在各个季节的分布情况,由表3可以看出,春季出现逆温的比例明显要高于其他季节,因此春季稳定状态占的比例较高可能是逆温现象引起的,同时也说明大气稳定度分类基本准确。
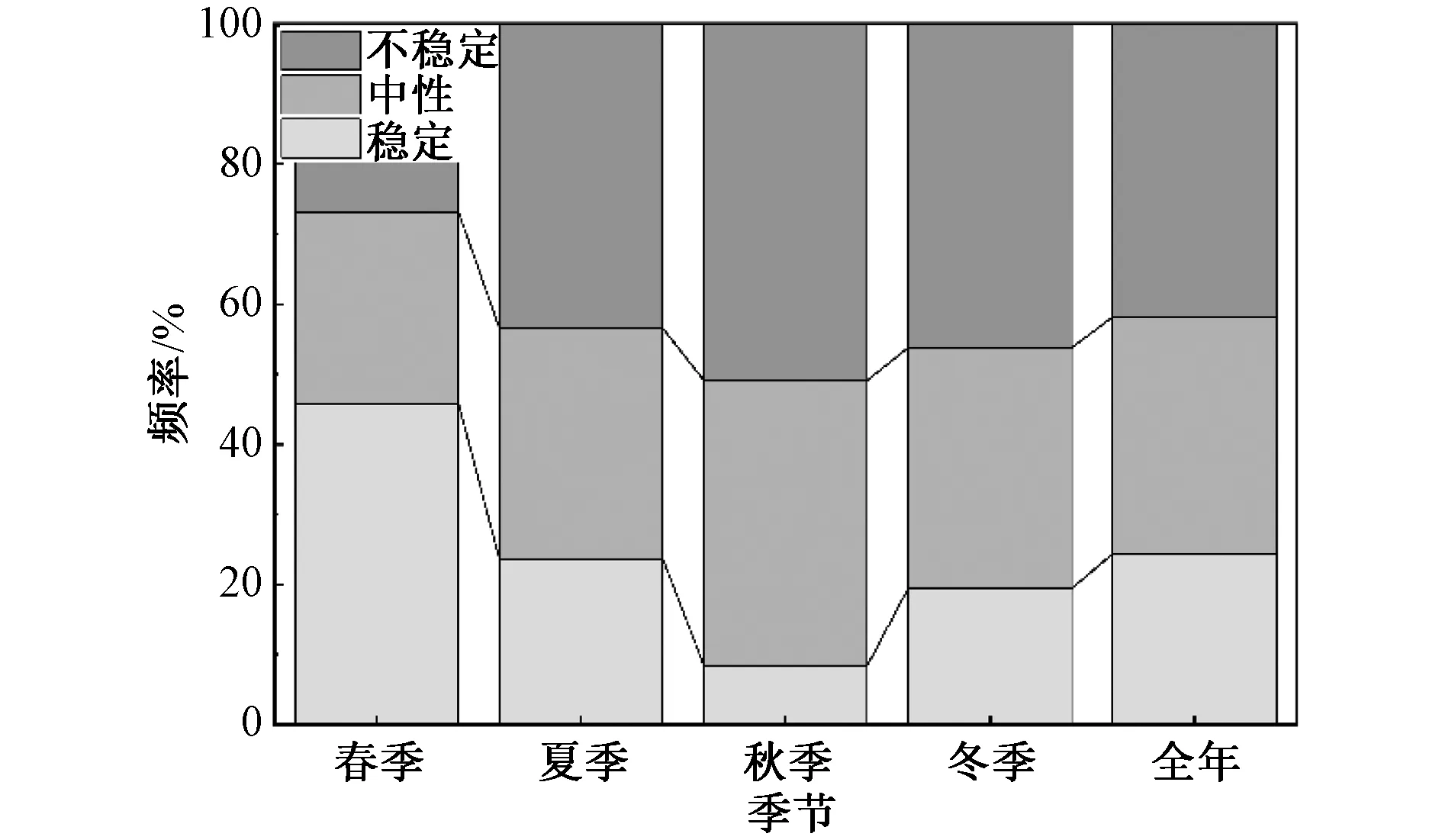
图3 不同季节大气稳定度分类Fig.3 Classification of atmospheric stability by season

季节春夏秋冬全年比例/%7.853.081.203.2215.35
图4及图5分别为不同高度的风速图及70 m与90 m风速相关性分析。由图4可以得出,10 m高度风速与其他高度风速之间差别较大,其他高度层尤其是60 m以上,风速差较小,可以看出海上风能资源随高度的变化较小,且该规律也说明在外推风速时,尽量将相近的高度层风速作为基准风速。图5是本文拟采用的基准高度70 m 及外推高度90 m风速之间的相关性。

图4 不同高度风速Fig. 4 Wind speed of different heights

图5 70 m和90 m高度风速相关性Fig. 5 Relevance of wind speed at 70 m and 90 m
3.2.2 风切变指数
空气运动因受湍流粘性和下垫面摩擦的影响,风速随高度的增加而增加的变化规律用风切变指数来表征。风切变指数是确定风电场风力发电机组选型及其安装高度的重要依据,其大小反映风速随高度增加的快慢。在风力发电资源评估过程中,轮毂高度通常在70~140 m之间,但是测风塔高度一般达不到轮毂高度,就需要用风切变指数外推轮毂高度风速[20]。
计算了不同高度层的风切变指数,如图6所示,1号风电场全场平均风切变指数仅为0.053 2,明显低于陆上大部分风电场。不同高度差之间的风切变指数变化趋势基本一致,但是12月和1月部分高度出现了负切变,且由于大气状态较稳定,各高度之间风切变指数相差较大。
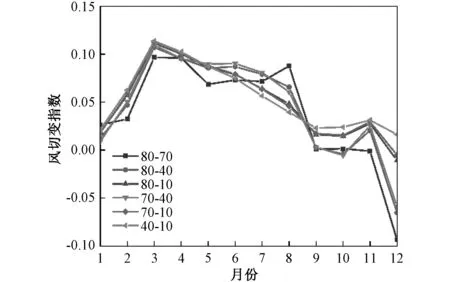
图6 不同高度差的风切变指数Fig. 6 Wind shear exponent at different height interval
3.2.3 湍流强度
湍流强度是10 min内风速随机变化幅度的大小,反映的是风速的波动情况[21],其变化和大气稳定度密切相关[22],产生湍流的原因主要有两个,一个是气流流动时,会受到海面粗糙度的摩擦或者阻滞作用,另一个是空气密度和大气温度差引起的气流垂直运动[23]。这两个原因正好对应海面动力学粗糙度和大气稳定度影响,图7是不同大气稳定度下的风廓线,图8是不同稳定度下的湍流强度。

图7 不同稳定度下风廓线 Fig. 7 Wind profile of different atmospheric stability

图8 不同稳定度下湍流强度Fig.8 Turbulence intensity of different atmospheric stability
1号风电场90 m年平均风速和年平均湍流强度分别为6.122 m/s,0.108。由图7和图8可以看出,大气稳定度影响风速及湍流强度的垂直分布。综合来看,风速和湍流强度随高度的变化规律正好相反,且均受大气稳定度影响。在稳定情况下,由于各层之间气流的垂直交换少,导致湍流强度的变化不全符合高度越高,湍流强度越小的变化规律。中性情况下风速及湍流强度的垂直分布与全年平均水平最为接近,这是传统风资源评估假设大气状态均为中性的依据,但是为了进一步提高风电项目落地的经济性和稳定性,应充分考虑大气稳定度对风资源评估各参数的影响。
3.3 模型计算结果
为了验证本文提出的基于中性等效风速的海上风廓线模型的实际应用效果,用两个海上风电场实测数据分别采用以下两种方法外推轮毂高度风速,并与轮毂高度实际风速比较,利用选定的评价指标评价不同方法的准确性和可靠性,设轮毂高度为90 m,基准层风速均为70 m。
方法一:目前风资源评估中常用外推方法,即用全场平均风切变指数外推轮毂高度风速;
方法二:用本文提出的基于中性等效风速的海上风廓线模型外推轮毂高度风速。
表4为分别用两种外推方法得到的平均风速及用最小二乘法拟合的风速威布尔分布参数,图9、图10分别为两个风电场风速和风功率密度的均方根误差及平均绝对误差。

表4 不同方法外推得到的海上风电场风资源参数Tab.4 Offshore wind resource parameters by different extrapolations

图9 1号风电场风速及风功率误差Fig. 9 RMSE and MAE of 1# wind farm

图10 2号风电场风速及风功率误差Fig.10 RMSE and MAE of 2# wind farm
表4分别从轮毂高度年平均风速、风功率密度、风速分布三个维度度量基于中性等效风速的海上风廓线模型的外推效果。由表中数据得到,方法二的优势在两个风电场中均有体现,尤其是2号风电场,外推得到的平均风速、风功率密度及风速分布参数都较传统方法更接近实测值。在海上风电场发电量计算过程中,风功率密度及风速分布参数都是极其重要的因子[24],其越接近实测值,越能更好地模拟海上风资源垂直分布,风资源评估结果就越接近实际储量。由于风功率密度和风速是立方关系,因此在大风速下由外推带来的评估误差就会更加显著。2号风电场年平均风速比1号风电场高1.246 m/s,两个风电场由方法一得到的年平均风功率密度绝对误差分别为5.8 W/m2和41.8 W/m2,而方法二为0.8 W/m2和19 W/m2,可以得到模型在大风速下的鲁棒性更强。
由图9、图10可以得到,以平均绝对误差和均方根误差为确定性外推精度评价指标,所提模型改善外推精度的效果明显。其中,风速均方根误差在两个风电场内可降低0.03 m/s到0.37 m/s,风功率密度均方根误差在两个风电场内可降低9.04 W/m2到83.58 W/m2;模型的风速及风功率密度平均绝对误差在两个风电场内均低于传统外推方法。综合来看,基于中性等效风速的海上风廓线模型在不同风电场外推过程中取得了较理想的计算效果,为更精确的海上风资源评估提供了参考依据。
4 结 论
针对海上风电机组轮毂高度高于测风塔高度、外推精度难以保证的问题,根据2座海上测风塔的实际测风资料,综合分析研究了海上风资源的评估参数及模型,并提出了基于中性等效风速的海上风廓线模型,得到以下几个结论:
(1) 海上风资源特性明显区别于陆上,主要表现在平均风速大、风切变低、海洋表面动力学粗糙度持续性变化,因此陆上风资源的时空分布研究方法不适用于海上,不宜用陆上风切变模型拟合海上风廓线。
(2) 海上测风阶段,除测量不同高度的风速、风向外,还应测量至少在两个高度层的温度,以计算大气稳定度参数,提高风资源评估精度。
(3) 大气状态时刻都在发生变化,且中性状态所占的比例较小,出现逆温的比例也会影响大气稳定度分布,进而影响海上风资源分布。
(4) 提出了基于中性等效风速的海上风廓线模型,且所提模型的风速均方根误差在两个风电场内可降低0.03 m/s到0.37 m/s,风功率密度均方根误差在两个风电场内可降低9.04 W/m2到83.58 W/m2,均优于传统外推方法,为海上风资源评估工程实际应用提供了参考。
