基于MPC的综合能源微网非线性鲁棒能量管理

田 旭， 王 炜， 黄存强， 王 猛， 李红霞， 郑天文

(1.国网青海省电力公司 经济技术研究院，青海 西宁 810000；2.清华四川能源互联网研究院， 四川 成都 610000；3.国网青海省电力公司，青海 西宁 810000)

0 引 言

现代能源供应系统需要高效的能源转换，以减少人类对环境的影响。供能系统中热电厂是集中供热的基础，它们能够利用从燃料中提取的不同温度能量，分别进行电能和热能的生产，以实现能源的梯级利用，其能源利用率高达80%[1]。近年来，随着适用于社区或工业设施的小规模热电联产厂规模化发展[2]，综合能源微网的概念被提出[3]，根据微电网的定义，微电网是一组相互连接的负荷和分布式能源，相对于电网来说，它们是一个单独的可控实体[4]。这一定义可以进一步扩展到包括热能，形成综合能源微网。

虽然热电联产电厂连接了热力和电力供应系统，但它们往往是分开运行的，特别是在能源管理方面。通常，优先考虑一种形式的能量，另一种是根据这个运行点可提取的最大能量确定的。随着监控、通信、控制和预测系统的飞速发展，有可能开发更先进的能源管理方案，利用现有的信息，以更经济和技术上实现有效的能源供应。最理想的控制方案是模型预测控制，它可以兼顾集中供热系统和热电联产电厂的所有特性。此外，经济模型预测控制概念在应用于热电联产能量转换过程控制时，将有助于提高能源利用效率。本文证明了经济非线性MPC在满足所有安全要求的同时，在能源供应的经济效率方面具有更好的效果。天气预测和市场价格的随机性要求控制具有鲁棒性，以确保极端情况下系统的灵活性。本文引入了一种实用的鲁棒优化，以确保系统将能够承受场景空间的外界，而不违反运行安全条件。

针对微电网能量管理问题的研究，主要集中在电方面，一个典型的例子是电能混合[5]，而热能很少被考虑。其他，还有微电网建模[6]，微电网的运行方法[7]，和能量管理的新算法[8]。与这些课题相比，电热联合能量管理的研究较少。文献[9]提出了一种基于混合整数线性规划的含热电厂微电网随机调度模型。然而，热分量仅被认为是被动需求，系统模型不是动态的。文献[10]考虑了一个联合的热电联产和暖通空调系统并执行基于遗传算法的优化。同样，该模型缺乏对热能需求的详细动态建模。文献[11]和[12]着重研究微电网运营的经济方面，而文献[12]则把这个问题放到了MPC的背景下。这两篇论文都忽略了系统动力学和热能需求模型。文献[13]通过对建筑热交换的详细建模，建立了热能需求的动态模型。然而，所提出的模型采用线性MPC，逼近各种非线性，但所建立的模型忽略了热网络。文献[14]在区域能量控制中采用了数据驱动的鲁棒预测控制。该方法的重点是基于历史数据的扰动识别。得到的模型用有限维线性程序近似。与文献[14]中提出的方法相比，本文更关注集中供热系统的详细非线性模型和详细的市场关系建模，而较少关注干扰集成。本文考虑了电/热联合环境下的集中供热系统建模问题。文献[15]提出了一个详细的集中供热网与电网的非线性模型，其重点是对联合电/热网络的分析，而不是控制。此外，需求建模为静态热负荷。该模型将作为集中供热网络液压元件模型的基础。

基于此，本文提出了一种基于非线性经济模型预测控制的综合能源微网能量管理方法，以提高能源的综合利用率。本文具体创新点为：(1)本文采用非线性经济MPC对综合能源微网能量管理进行精确建模，该方法可解决区域供热系统数学建模中遇到的非线性问题，与传统的线性MPC方法相比，该方案的复杂性要大得多，但随着计算能力的发展，该控制方案将会成为一种实时的解决方案；(2)本文中发电厂与用户侧的综合能源微网分别作为不同利益主体参与电热市场的竞争，故本文将系统运行的经济结果反馈到过程控制的能力中，并在系统控制中设定了一个实际目标；(3)本文采用建筑热动力学和天气/习惯预测对能源网络和建筑物进行了建模，此外，考虑到预测的不确定性，本文还在模型中增加了鲁棒优化，以应对天气预测的误差和负荷需求的不确定性。

1 综合能源微网的系统概述

图1为综合能源微网的一般示意图。它包括能源生产方的热电联产电厂和能源需求方的区域热电网的建筑物，这些建筑属于小型能源系统，吸收太阳能，并根据居民的习惯提供热能，电能也是如此。建筑的屋顶上集成了光伏板，剩余的电力消耗高度依赖于天气和用户用能习惯。该系统具有中央管理单元，每个建筑设置其所需的温度，并将其与中央管理单元通信。

图1 综合能源微网的一般示意图Fig. 1 Microgrid model block diagram representation

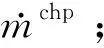
图1的系统的中心部件是热电联产装置。根据系统的再加热器和泵的设计，火力发电厂的数学模型有很大的不同。由于本文的重点是网络优化和能量优化，因此将采用简单的单涡轮模型。这种热电厂的动力学更简单，下面的模型描述了能量输出对控制信号的响应:

(1)

(2)

式中：Tchp,p和Tchp,q分别为控制电能和热能转换的供热阀门的时间常数。根据提取的能量(热和电)，输入的热量将进行校正，以达到预期的提取。输入热量由提取的能量和装置的能量转换效率确定:

(3)

式中：Qin为输入热量；η为能量转换效率。上式表明，能量转换效率为两种形式提取能量的函数。这个函数通常用三阶多项式来描述:

η=Υ1+Υ2Pchp+Υ3(Pchp)2+Υ4(Pchp)3+

(Υ5+Υ6(Pchp)+Υ7(Pchp)2)(Qchp)+

Υ8(Qchp)2

(4)

为了正确地描述能量转换过程，需考虑热电厂的运行约束。由于能量转换过程的不同特性，热电厂的运行范围被限制在一个特定的区域。图2描述了热电联产电厂的能量转换效率和典型运行范围。

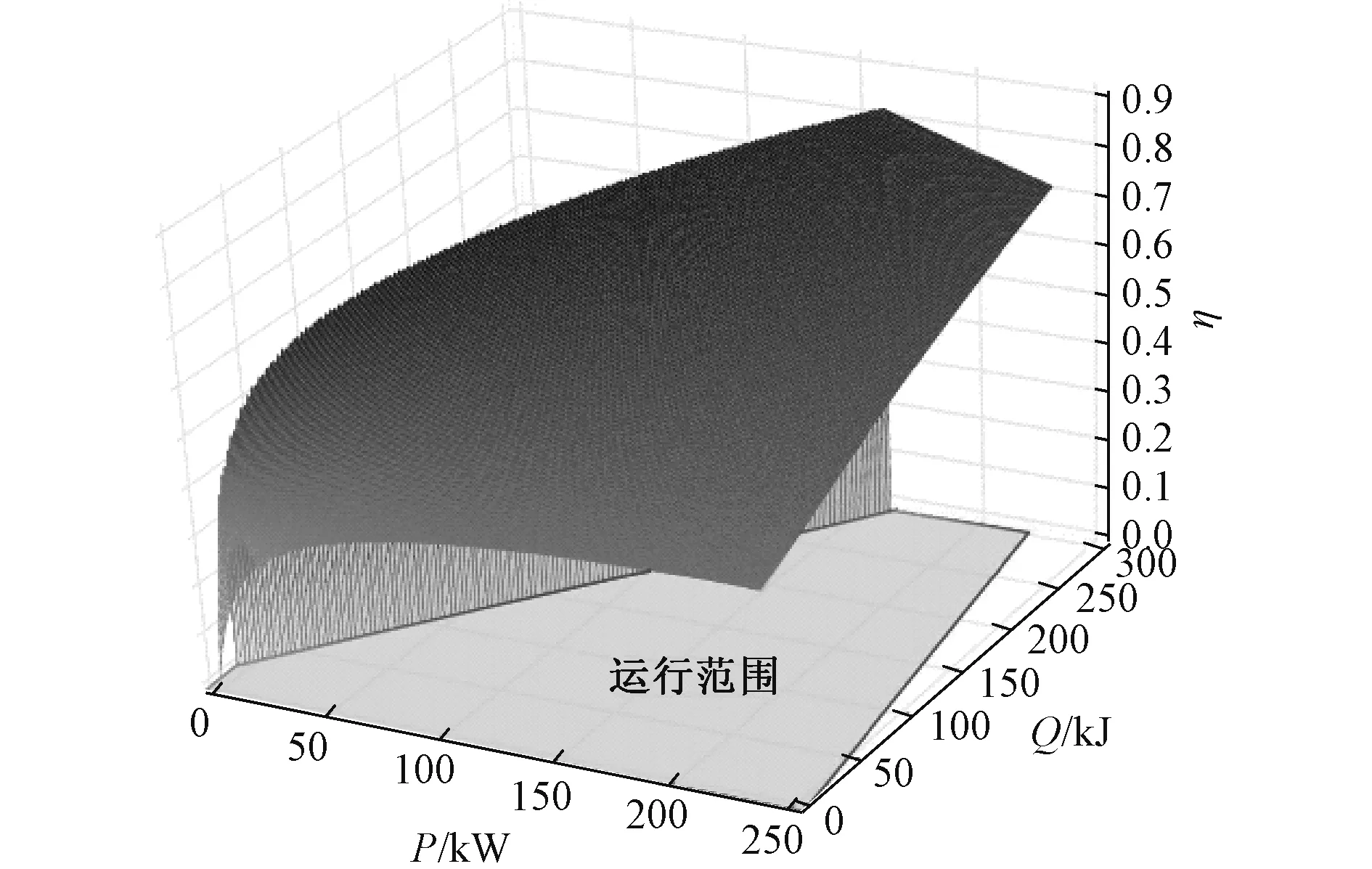
图2 热电厂的运行范围和能源效率Fig. 2 Operating range and energy efficiency of plant

上图中的运行范围可以用一组N个线性不等式来描述:

AiPchp+BiQchp+Ci≤0，i=1…N

(5)

提取的热量进入热交换器，并被转移到循环水中，循环水将热量通过供应网络供应给消费者。消费者通过散热器使用这些热量，以保持建筑所需的温度。因此，热量需要补偿由于建筑和环境之间的交换而损失的热量。在为建筑物供热后，循环水被返回到工厂的热交换器中，在那里它被重新加热。下述将详细介绍供热系统的通用模型，从拓扑上看，供热系统可以看作是一个有向图G= (N,B)，有节点、分支和各自的矩阵:连接节点到分支的关联矩阵A，连接回路到分支的环路关联矩阵B。此外，还需要两个位置矩阵和一个位置向量来保持模型的通用表示。第一个位置矩阵记作C，将建筑物与节点连接起来。第二个位置矩阵D，连接热市场和节点。最后，向量E将CHP工厂连接到一个节点。热网络实际上是一个水力网络，它的状态可以完全由水力定律决定，故本文采用这些定律的节点公式。如第一定律是质量守恒原理，表述如下:

(6)

第二定律是能量守恒原理，表述为

(7)

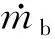
(8)

吸收/释放的热量决定了住宅建筑的温度动态变化。如果将此表达式纳入一个封闭系统的温度动力学一般定律中，则每座建筑的热方程可对应如下：

(9)

下一组方程与市场交易有关,交换热能由下式确定:

(11)

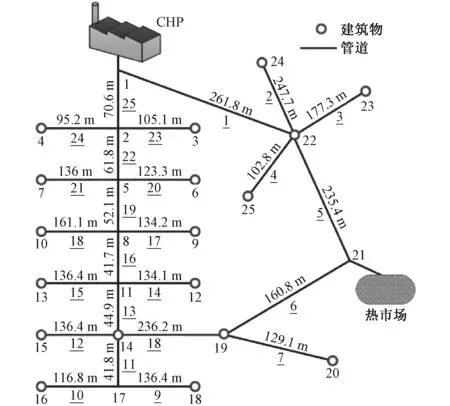
式中：cp是水的比热容。交换电量确定为

Pgrid+-Pgrid-=Pchp-Prl,Pgrid±≥0

(12)

(13)

(14)

(15)

2 基于MPC的非线性鲁棒能量管理

2.1 物理模型及目标函数

集中供热运行中最重要的要求是在众多影响建筑温度的外部参数之后，保持住宅建筑所需的温度。此外，建筑的电力需求也必须得到满足。满足热电需求是综合能源微网运行的首要目标。由于该系统与外部市场的互连具有灵活性，因此，决策过程的第二个组成部分是经济性质的。根据市场情况，从外部市场购买热/电或生产和出口可能具有成本效益。此外，由于价格不对称，减少任何交易并满足微网内的需求可能具有成本效益。这里采用的市场假设高速率交易，这意味着实时运行紧随交易，计划与交付的能量偏差可以忽略不计，不会造成不平衡惩罚。目前这种交易方式并不常见。但是，随着智能电网的发展，这有望成为未来市场的普遍做法。能量管理的总体目标可以分为两个不同的组：跟踪目标和经济目标。跟踪目标与建筑内部的温度控制有关，需要根据居民的舒适偏好来维持所需的温度。为此，在目标函数中采用了二次罚项，实现更灵活的温度跟踪。然而。严格的温度跟踪可以对经济状态动态进行清晰的分析，并与传统方法进行精确的比较。经济目标与热/电市场交换和生产成本有关。所有这些目标都可以定义为以下函数的最小化：

J(X(·),U(·),Θ(·))=

(16)

式中：λe±为电的买卖价格；λq±为热的买卖价格；λfuel为燃料价格。上式中权重α是必要的，以便设定温度跟踪相对于目标经济部分的重要性，故这个权重将被设置为104。

2.2 MPC的规划周期

模型预测控制在严格的形式下是无限水平控制问题的有限水平近似。找到一个合适的有限视界近似是一项困难的任务，对于具有长期存储的系统来说，情况更加复杂。另一方面，在更大范围内参数的不确定性允许在更低范围内宣布更高的重要性。如果上述系统在其性质上具有特定的周期性，则适当地组织相应的能量管理。在区域供热系统中，可以识别出一个特征日周期性，并根据日周期性设计热储。因此，终端约束为

Ts(24h)=Ts,full

(17)

式中：Ts,full是系统额定供电温度。计划的时间跨度将从t0到这一天结束。这意味着规划范围将随着时间的推移而减少，直到新的计划规划范围开始的那一天结束。

2.3 鲁棒模型的建立

一天开始时的运行计划是一天为优化单位。就参数预测而言，这是一个长期的过程，在MPC的制定中必须考虑参数预测的不确定性。鲁棒公式将控制轨迹推离边界范围，以使自由响应不同场景的实现。为了实现这一点，将两种极端的场景区分为完整场景集的包络。这种极端轨迹在参数实现中的概率很小。需要指出的是，鲁棒轨迹通常会带来经济损失。然而，这种损失被认为是可以接受的。可以采用一个更严格的公式，以便更精确地根据风险来计算这种经济权衡。然而，这超出了本文的研究范围。为了构建鲁棒模型，模型中的每个状态、控制和参数将被表述为场景相关的参数，即每个状态/控制轨迹对应于每个不确定参数的场景轨迹。每个场景用表示，所有场景的集合为Ωξ={exp,min,max}，其中exp为预期情景，min和max为极端情景。预期情景与式(16)中所述的原始确定性问题有关。该情景支配预期的经济交互作用。另一方面，会引入极端情况的鲁棒性，确保系统能够安全运行，极端情况下对经济较少关注的。将Θ,X和U变成了Θξ,Xξ和Uξ，并且在原问题中加入了额外的约束集。完整优化问题可表述为

g(Xξ(τ),Uξ(τ),Θξ(τ))=0,

h(Xξ(τ),Uξ(τ),Θξ(τ))≤0,

Uexp(τ0)=Umin(τ0)=Umax(τ0)

(18)

式中：πξ代表每个目标的权重因子。这个因素通常反映每个场景的概率。该问题的最后一个约束保证了当前控制回路中控制信号的唯一性。这个约束连接所有场景。此外，耦合是通过目标的跟踪组件来执行的。也就是说，在每一种情况下，目标都是在建筑物中保持理想的温度。因此，对于所有场景，问题(18)都是同时解决的。

2.4 求解策略

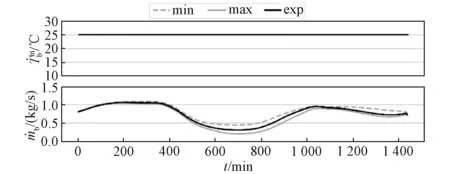
式(18)中定义的优化问题是由微分和代数方程组成的最优控制问题。这类问题通常通过一系列称为直接法的数值方法来解决，该方法是通过状态和控制函数的时间维度离散化，将原始问题转化为非线性约束优化问题。在这个过程中，无限维的时间空间被近似为有限维的时间空间。本文将采用搭配法。首先，该方法把每个控制区间[tk,tk+1]分成一个用ng+ 1个点以h为间隔的等距网格tk，0

(19)

式中：xk,j,i为多项式系数，Pi(τ)为d阶的拉格朗日多项式基:

(20)

配置点tr通过Radau方案选择。状态导数为

(21)

为了实现连续性，有必要将所有相邻的间隔用下列方法连接起来:

j=0,…,nj-1

(22)

这些近似方法将原始问题转化为非线性优化问题。

3 仿真验证

以图3所示的某热网为例，验证了本文提出的MPC能量管理的有效性。在该网络中引入的热交易市场。

图3 某海岛热电网络Fig. 3 Thermoelectric network of an island

模型参数Θ取自文献[16-19]中的温度和太阳辐照参数，剩余载荷通过对典型载荷数据的缩放得到。除了这些轨迹之外，我们还使用自回归模型模拟了一系列情景，以在预测时纳入不确定性。这些场景如图4所示。

图4 场景参数Fig. 4 Parameters scenarios

图4中黑线和红线分别为期望场景和极端场景，期望的建筑温度为25 ℃，电力销售价格为60元/MW·h，电力购买价格为150元/MW·h。该模型在Intel i7机器上使用Python(PYOMO)环境中的IPOPT求解器，模型的采样时间为1 min。离散化步骤数为100个，每个分段上有3个配置点。典型求解时间在第一次运行的2 min范围内。然而，当算法在循环中实现，并且解决方案可以在每次运行时作为初始化转移时，这一时间将进一步减少。由于我们处理的是低时间常数的热系统，这种性能是令人满意的。所提出的控制方案将适用于两种运行模式:在供热方面的孤岛模式和互联模式。

图5为热电联产的输入热、输出热和供应温度的状态轨迹。黑线表示预期场景，灰线表示极端场景，红线表示运行范围。输入热量是热量和电能的输出以及相应的转换效率的结果。第二种状态是CHP的热输出。

图5 热电联产输入热、输出热、供应温度和交换质量流量的状态轨迹Fig. 5 State trajectories for CHP input heat, CHP output heat, supply temperature, and grid exchange mass flow rate

由上图可知，一个典型的下降在一天的中间。这是由于环境温度升高导致热需求下降的结果。供应温度的变化趋势与此相反。这意味着热能被储存在CHP蓄热器中，而不是额外减少热量输出，从而导致低效率的运行点图6为建筑1的温度和质量流量的轨迹。

图6 建筑物1温度和质量流量的状态/控制轨迹Fig. 6 State/control trajectories for Building 1 temperature and mass flow rate

由上图可知，通过改变建筑质量流量来维持25 ℃的理想温度。同样，随着环境温度的升高，在中午可以注意到一个明显的下降。假设一个相互关联的状态，其极限为±2 kg/s。假设固定的供应温度符合交易所必需的供应质量标准。在这种情况下，可以获得更便宜的热源。因此，其会最大限度地从电网输入热量。因此，进口热的质量流率是最大的，除了在图7中可以看到的一个短暂的时段。这将导致CHP输出热量的减少。CHP的热输出被最小化到一个转换效率降低的点，同时，电力侧的工作范围缩小。图8显示，与孤岛状态一样，温度保持在理想水平。虽然两种情况下的热需求是相同的，但由于供应温度的不同，在这种情况下质量流量略有不同。两种情况下的电力市场状况是相同的，但轨迹不同。图9显示了这些轨迹。与孤岛运行相比，它增加了中午的电力进口。这是在上面解释的热输出减少后，电力运行极限改变的直接结果。由于电力进口的增加而带来的经济损失是合理的，因为进口的热量更便宜，从而避免了燃料成本。

图7 热电联产的输入热、输出热、供应温度和电网交换质量流量的状态轨迹Fig. 7 State trajectories for CHP input heat, CHP output heat, supply temperature, and grid exchange mass flow rate

图8 建筑物1温度和质量流量的相互连接的状态/控制轨迹Fig. 8 Interconnected regime - state/control trajectories for building 1 temperature and mass flow rate

图9 热电联产电力输出和电力交换的状态/控制轨迹Fig. 9 Interconnected regime - state/control trajectories for CHP electric power output and electric power exchange

为了指出所提出的MPC框架的主要优点，有必要将其与传统方法进行比较。传统和本文所提方法的成本结构如表1所示，传统情况下换电的利润更高。然而，这一利润不能补偿总输入热量增加的燃料成本。本文所提方法的总成本要低612.6元。每天的成本降低9.75%。所提方法的总成本要低545.5。每天的成本降低了9.11%。这证明了综合能源微网的经济模型预测控制的好处。在保持理想舒适水平的同时，可以实现显著的节省。

表1 传统和所提MPC框架的成本比较

4 结 论

在现代能源系统中，需要同时考虑电能供应和热能供应。本文考虑了综合能源微网，该微网的中心部件是连接电和热供应系统的热电联产装置。基于鲁棒非线性经济模型预测控制提供了一个具有高模型精度的综合能量管理系统。此外，还引入的鲁棒性为系统参数实现中的极端轨迹做好了准备，从而保证了系统的安全运行。控制目标的经济性质描述了控制轨迹的经济后果。这种方法在容许轨迹的集合中寻找最经济可行的轨迹。因此，所提出的方法符合能源系统发展的预期。