实测类噪声数据辨识所得负荷模型参数的时变性和分布性研究

陈 茜， 王 卫， 王 颖， 吴沛萱， 王海云， 陆 超

(1.国网北京市电力公司 电力科学研究院， 北京 100075；2.国网北京市电力公司 电力调度控制中心， 北京 100031；3.清华大学 电力系统及发电设备控制与仿真国家重点实验室， 北京 100084)

0 引 言

负荷建模是电力系统稳定分析重要而困难的关键环节。采用不合适的负荷模型会得到不准确的分析结果，极端情况下甚至得到完全相反的稳定性结论[1-3]。近年来，电力负荷侧变得越来越复杂，为此，建立与实际负荷特性相符的模型变得更具挑战[4-8]。

此外，电力负荷具有时变性和分布性，不同站点在不同时间辨识所得模型参数存在一定的差异，为探究电力负荷的时变性和分布性，国内外研究学者分别采用统计综合法和总体测辨法开展了大量的研究工作。WECC模型和校验工作组(Modeling and Validation Work Group, MVWG)采用统计综合法统计得到WECC12个气候区在5个典型日的负荷模型参数[9]，华北电网则针对76座典型220kV变电站开展详细调查，建立了考虑配电网络的综合负荷模型[10]，此外，文献[11]采用总体测辨法辨识得到不同站点的负荷模型参数，文献[12-13]则采用不同时间的量测数据，辨识得到同一站点在不同时间的辨识参数，进一步文献[14]采用鲁棒性的参数辨识方法来跟踪负荷模型参数的时变性。一方面上述研究虽在一定程度上体现了电力负荷的时变性和分布性，但仅得到典型站点在典型时段的辨识参数，难以在全网范围内实时进行；另一方面，电力负荷的时变性和分布性对系统仿真的影响研究并未涉及。

近年来，广域测量系统的发展可准确捕捉电力系统的实际动态，为负荷建模研究提供了重要的数据来源[15]，同时现有研究表明，电力系统正常运行状态下的小幅扰动数据可用于电力系统的机电动态分析[16]，在此基础上，基于类噪声数据的负荷模型参数辨识方法得以提出[17，18]，为实时跟踪电力负荷的时变性和分布性提供了科学的思路和有效的解决方案。现有基于类噪声数据的负荷模型参数辨识研究解决了负荷模型结构选择和参数辨识方法的基本问题，同时从不同角度对辨识参数的有效性进行了综合验证[19，20]。在此基础上，本文针对实测类噪声数据，辨识得到不同站点在不同时间的负荷模型参数，分析辨识参数的时变性和分布性规律，进而从系统仿真角度指出研究电力负荷时变性和分布性的重要性和必要性。

本文首先简要介绍基于类噪声数据的负荷模型结构和相关参数辨识方法；进而对辨识参数的时变性和分布性分析的基本思路进行详细说明；最后通过电力系统实际量测数据对本文研究思路进行综合验证，指出在全网范围内实时开展负荷模型参数辨识的重要意义。

1 基于类噪声数据的负荷模型参数辨识

负荷模型参数辨识主要包括模型结构选择和参数辨识两个关键环节。

1.1 综合负荷模型结构

综合考虑类噪声数据波动较小和系统仿真对模型简便性的要求，本文以图1所示恒阻抗并联感应电动机的综合负荷模型结构为例进行分析：

图1 恒阻抗并联感应电动机模型结构Fig. 1 The structure of constant impedance paralleling induction motor

由图1可见，电压幅值U和电压相角θ为输入，有功功率P和无功功率Q为输出。R和Xp分别为静负荷的电阻和电抗，Xs和Xr为感应电动机定子电抗和转子电抗，Xm为励磁电抗，Rr为转子电阻。

针对感应电动机模型，为便于分析计算，图1所示电路参数转化为如下形式：

(1)

进而，采用如下三阶状态方程来描述感应电动机的动态特性：

(2)

(3)

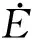
(4)

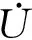
针对恒阻抗模型，考虑到静态电抗Xp可以包含到等效感应电动机模型中，因而待辨识参数只包括静态电阻R。

为此，恒阻抗并联感应电动机的综合负荷模型待辨识参数包括：

[X,X′,T′d0,H,R]

(5)

除上述待辨识参数，综合负荷模型一个重要参数是动静负荷比例：

K=(U2/R)/P

(6)

即动静负荷比例描述的是静负荷消耗的有功功率所占的比例。

1.2 参数辨识方法

图2 基于类噪声数据的负荷模型参数辨识Fig. 2 Ambient signal based load model parameter identification

其中，预测输出Pp和Qp的详细计算公式可参考文献[18]，这里不再展开，然后采用差分进化算法优化得到满足如下目标函数的辨识参数：

(Qp(k)-Q(k))2]

(7)

式中：P和Q为实际量测有功功率和无功功率。Pp和Qp为模型预测有功功率和无功功率。kend为参数辨识数据段长度。

在辨识得到机电参数后，根据式(2)中第一个方程可得计算滑差s，同时，式 (2)中第二个方程的积分形式如下：

(8)

需要指出，考虑到实际类噪声数据波动较小，机械参数不易辨识，因此本文不再考虑。

2 辨识参数的时变性和分布性研究思路

本文采用图3所示思路从实测数据辨识参数的分析和系统仿真角度对辨识参数的时变性和分布性进行分析验证：

图3 辨识参数的时变性和分布性研究思路Fig. 3 The basic idea to study the time-varying and the distributed characteristics of power loads

(1) 针对实际系统的类噪声量测数据，辨识得到不同时间和不同站点的负荷模型参数；

(2) 针对实际系统发生的故障扰动数据，用实测类噪声数据辨识参数替换仿真系统固定参数进行仿真，通过仿真数据和故障扰动数据的对比来完成辨识参数时变性和分布性的验证。

3 实测数据辨识参数的分析验证

本文从实际量测出发，从不同角度对辨识参数的时变性和分布性进行分析验证。

3.1 实测数据介绍

2018年8与19日16∶03左右实际系统发生BC相相间故障，为体现电力负荷的时变性，分别采用2018年8月19日16∶00和2018年9月16日11∶00实测类噪声数据进行负荷模型参数辨识，同时，为体现电力负荷的分布性，针对实际系统中SX、ZJ和HL三个站点的实测数据辨识所得模型参数进行分析。

在上述基础上，分别用不同时间和不同站点辨识所得模型参数替换仿真系统中的固定模型参数，从系统仿真角度对辨识参数的时变性和分布性进行综合验证。

3.2 实测类噪声数据辨识参数

以2018年8月19日16∶03左右SX站实测类噪声数据为例，图4所示为该站点的实际量测数据和相应量测的频谱：

图4 实际量测数据和相应数据的频谱Fig. 4 The field PMU measurements and their corresponding spectrum

其中，图4 (e)～(f)分别为图4 (c)～(d)所示有功功率和无功功率的频谱，由此可见类噪声数据是电力系统在正常运行状态下的小幅扰动数据，同时，类噪声信号频谱集中在2 Hz以内，这与机电暂态频谱范围相一致，由此表明基于类噪声数据参数辨识的可行性。在此基础上，以图4 (a)～(b)所示16 s电压幅值和相角为输入，图4 (c)～(d)所示16 s有功功率和无功功率为输出，辨识所得模型参数如表1所示。

表1 实测数据辨识所得模型参数

针对表1辨识所得模型参数，图5 (a)-(b)所示分别为辨识参数的有功功率和无功功率拟合曲线：

图5 辨识参数对实测数据的拟合曲线Fig. 5 The fitting curves of the identified load model parameters

其中，实线为实际系统量测输出，虚线为辨识模型的预测输出。为进一步量化辨识所得模型参数对实际量测曲线的表征能力，定义如下所示拟合度指标：

(9)

式中：y为实际量测数据输出，yp为模型预测输出，且输出包括有功功率和无功功率；mean(·)为向量的均值；拟合度的取值范围为[-∞，1]，且dfit=1表示完全拟合。图5所示有功功率和无功功率的拟合度分别为0.875 8和0.908 4，可见，辨识所得模型参数可以较好的拟合实际量测数据，由此表明辨识参数的有效性。在此基础上，取典型值H=2.0，假设Rs=0，Xs=Xr，将实测数据辨识参数根据式(1)转化为BPA格式的模型参数，如表2所示：

表2 BPA格式的辨识参数Tab.2 The identified load model parameters in BPA form

至此，实测数据辨识所得负荷模型参数可应用于BPA仿真系统。

3.3 辨识参数的时变性和分布性分析验证

进一步针对实际系统量测数据，从不同角度对辨识参数的时变性和分布性进行分析验证。

3.3.1 辨识参数的时变性和分布性分析

采用2018年8月19日故障前实测类噪声数据辨识所得相关站点的模型参数如表3所示。

表3 采用8月19日类噪声数据辨识所得模型参数

为体现辨识参数的时变性，采用2018年9月16日11∶00实际量测数据辨识所得负荷模型参数如表4所示：

表4 采用9月16日类噪声数据辨识所得模型参数

由表3和表4所示辨识结果可见，一方面相同时间不同站点辨识所得模型参数存在一定的差异，由此表明电力负荷的分布性，另一方面，相同站点在不同时间辨识所得模型参数也不相同，由此体现了电力负荷的时变性。

3.3.2 辨识参数的时变性和分布性验证

(1) 时变性验证

在3.3.1节辨识参数的基础上，得到如下三个场景的量测或仿真数据如图6所示。

图6 实测数据和采用不同时间辨识参数所得仿真曲线Fig. 6 The comparison between measurements and simulation curves obtained with load model parameters identified during different times

场景1：实际量测数据；

场景2：采用表3所示故障前类噪声数据辨识所得模型参数替换仿真系统中相应站点固定参数所得仿真曲线；

场景3：采用表4所示非故障相近时间类噪声数据辨识所得模型参数替换仿真系统中相应站点固定参数所得仿真曲线。

进而，定义不同曲线之间的距离d如下所示。

(10)

式中：Vm为实际系统量测数据；Vs为仿真所得数据；n为样本点数据。则图6 (a)～(b)所示仿真曲线与实际量测数据的距离分别如表5和表6所示：

表5 ZJ站实测数据和仿真曲线的距离(1)

表6 ZC站实测数据和仿真曲线的距离(1)

由图6、表5和表6所示结果可见，采用故障相近时间辨识参数所得仿真曲线与实际量测数据较为接近，这在一定程度上表明了实测类噪声数据辨识所得模型参数的有效性。同时，采用故障相近时间辨识参数所得仿真曲线较采用其它时间辨识参数所得仿真曲线与实际量测数据更为接近，由此表明电力负荷的时变性及实时辨识负荷模型参数的必要性。

(2) 分布性验证

进一步，得到如下三个场景的量测或仿真数据如图7所示。

图7 实测数据和各站点采用不同辨识参数所得仿真曲线Fig. 7 The comparison between measurements and simulation curves

场景1：实际量测数据；

场景2：采用表3所示各站点辨识所得模型参数替换仿真系统中相应站点固定参数所得仿真曲线；

场景3：采用表3所示ZJ站辨识所得模型参数替换仿真系统中三个站点固定参数所得仿真曲线。

根据式(10)所示距离度量，图7 (a)～(b)所示仿真曲线与实际量测数据的距离分别如表7和表8所示：

表7 ZJ站实测数据和仿真曲线的距离(2)

表8 ZC站实测数据和仿真曲线的距离(2)

由图7、表7和表8所示结果可见，各自站点采用各自量测数据辨识所得模型参数所得仿真曲线较各站点均采用ZJ站辨识参数所得仿真曲线与实际量测数据更为接近，由此表明电力负荷的分布性及在全网范围内开展负荷模型参数辨识的必要性。

4 结 论

本文以基于类噪声数据的负荷模型参数辨识方法为基础，从实测类噪声数据辨识参数角度对电力负荷的时变性和分布性进行分析，本文所得结论如下：

(1) 基于类噪声数据的负荷模型参数辨识方法可有效跟踪电力负荷的时变性和分布性；

(2) 不同站点在不同时间的辨识参数不同，由此体现了电力负荷的时变性和分布性；

(3) 实测数据和采用不同负荷模型参数仿真所得曲线的对比结果再次验证了电力负荷时变性和分布性，指出在全网范围内实时开展负荷模型参数辨识的重要意义。