降维虚同相轴法压制陆地层间多次波

谢飞 安圣培 朱成宏 刘嘉辉 胡天跃,

降维虚同相轴法压制陆地层间多次波

谢飞1安圣培1朱成宏1刘嘉辉2胡天跃2,†

1.中国石化石油勘探开发研究院, 北京 100083; 2.北京大学地球与空间科学学院, 北京 100871; †通信作者, E-mail: tianyue@pku.edu.cn

针对陆地层间多次波压制效果不明显的问题, 提出降维虚同相轴法, 实现叠前陆地地震资料的层间多次波压制。对经过精确动校正的叠前道集, 逐道应用虚同相轴法预测层间多次波, 实现降维处理。与传统的虚同相轴法相比, 运算量大大降低, 且不再要求炮检点规则且密集地分布。同时, 引入加权叠加的高信噪比参考道, 参与叠前道集的互相关和褶积运算, 提高了虚同相轴法的预测精度。将所提方法应用于中国西部地区实际陆地地震资料, 取得明显的层间多次波压制效果。

层间多次波; 虚同相轴; 降维; 互相关; 自适应相减

多次波是地震勘探中常见的相干噪声, 在海洋勘探和深层陆地勘探的地震资料中均会出现。常用的地震成像技术基于一次反射波信号的假设, 但多次波不满足该假设, 因此常被视为相干噪音, 会影响目的层信号的振幅、相位和频率, 并可能产生构造假象, 降低成像结果的可靠性和信噪比[1]。

多次波分为表面多次波和层间多次波。表面多次波是由地表反射产生的, 广泛存在于海洋勘探数据中, 压制表面多次波的方法较为成熟, 已经商业化, 在主流地震数据处理软件(如 GeoVision, Omega和 GeoEast 等)中均有相应的模块。层间多次波是由地层间多次反射产生的, 常见于深部陆地和部分海洋勘探数据中。层间多次波至少在地层间反射 3次, 振幅衰减较大, 只有在两个强反射界面间产生的层间多次波容易被观测到[2]。与表面多次波相比, 预测和压制层间多次波的难度更大。

随着陆地勘探的目标逐渐由浅层延展到深层, 由简单构造延展到复杂构造(如盐丘高速体、高倾角构造以及碳酸盐岩缝洞储集体等), 层间多次波的压制越来越受重视。与海洋勘探资料相比, 陆地勘探资料的信噪比通常更低, 使得陆地层间多次波的压制更具挑战性, 尤其是针对中国西部地区具有复杂地表条件的陆地地震资料, 鲜见好的层间多次波压制效果。

多次波压制方法通常分为滤波类和预测相减类[3]。常用的滤波类方法包括-滤波、-滤波、Ra-don 域滤波、预测反褶积[4]以及聚束滤波类方法[5‒6]等, 这些滤波类方法计算成本低, 计算效率高, 但精度不高。预测相减类方法是通过建模来预测多次波, 再通过自适应相减, 将预测的多次波去除, 达到压制的目的。常用的方法如下。1)波场延拓法: 将地表接收的波场反向延拓到地下, 得到地下某点的波场, 主要用于海上数据多次波的压制[7]。2)地表相关多次波压制法(surface-related multiple elimina-tion, SRME): 是一种基于反馈迭代的方法, 主要通过对输入数据的自褶积运算, 得到多次波的预测响应, 再通过自适应相减去除多次波, 广泛应用于表面多次波的压制[8‒9]。3)虚同相轴法: 通过互相关运算, 构建虚同相轴, 再与原始数据褶积, 得到层间多次波[10‒11]。虚同相轴法为数据驱动类方法, 计算量小于反馈迭代类方法。另外, 基于散射理论的逆散射级数法[12]和基于单边自聚焦系统的 March-enko 方程法[13]等均可用于多次波压制。

上述方法在表面多次波压制以及海上勘探资料的多次波压制方面取得不错的效果, 但对于叠前陆地资料, 层间多次波的频率和视速度等特征信息与一次波接近, 常用的滤波类方法对两者的区分能力有限, 难以保证压制层间多次波的同时不损伤一次波信号。

应用预测相减类方法有以下难点: 1)叠前陆地地震道集的信噪比通常较低, 影响多次波预测的准确性; 2)诸如 SRME 和虚同相轴法这类方法, 要求使用规则化数据, 并且要求足够密集的炮检点分布, 但中国西部地区的复杂地表条件难以满足这些要求。

针对上述问题, 本文提出降维虚同相轴法, 用于叠前陆地资料的层间多次波压制。输入数据为经过动校正的叠前共中心点(common mid-point, CMP)道集, 通过参考道构建、虚同相轴方法、多次波预测和自适应相减, 实现叠前陆地资料的层间多次波压制, 并应用于中国西部地区的实际陆地地震资料, 取得良好的效果。

1 方法原理

虚同相轴法最早由 Ikelle[10,14]提出, 思路是基于克希霍夫积分表示定理, 将地下反射层产生信号的基准面重置到自由表面, 再利用以自由地表为基准面的散射信号预测层间多次波。该方法中, 虚同相轴记录相当于波场延拓算子, 通过与原始地震数据褶积来预测层间多次波。这一过程与 SRME 方法类似, 只是 SRME 方法中以原始数据作为波场延拓算子[8]。如图 1 所示, 虚同相轴法预测层间多次波的实现过程如下。

第 1 步, 通过互相关构建虚同相轴记录。对来自地层2和3的一次反射波进行互相关运算, 图 1 (a)中灰色粗线标示两组反射波共用的射线路径, 其对应的旅行时在互相关过程中相互抵消, 由此构建2与3之间的虚同相轴记录, 其物理意义是以2处的虚拟震源为源点, 经3反射后在地表接收的地震记录。图 1(a)中虚线表示旅行时为负的射线路径,这一过程实现将地表某点激发的地震记录, 通过基准面重置, 得到地下某点激发的地震记录。选取不同地层的一次反射波, 可以得到以不同地层为基准面的虚同相轴记录。

(a)示意互相关构建虚同相轴记录; (b)和(c)分别为来自地层 w3和 w4 的一次反射波与虚同相轴记录褶积, 构建与 w2 有关的层间多次波。实线(虚线)表示旅行时为正(负)的射线路径, 灰色粗线表示共用的射线路径

第 2 步, 将虚同相轴记录与原始地震记录褶积, 构建层间多次波。如图 1(b)所示, 将3的一次反射波与2,3之间的虚同相轴记录进行褶积, 灰色粗线标示的共用射线路径具有正、负号相反的旅行时, 在褶积运算中相互抵消, 由此重构2与3之间的一组层间多次波。

第 3 步, 如图 1(c)所示, 使用来自地层4的一次反射波重复第 2 步, 可构建4,2,3间的层间多次波。同理, 只要使用来自不同地层的反射波, 就可以构建与2有关的全部层间多次波, 再通过自适应相减, 从地震记录中去除。本文的自适应相减采用基于 2 范数准则的多道最小二乘匹配方法[15], 将预测的层间多次波与叠前 CMP 道集中的多次波做振幅与相位的匹配, 再将经匹配后的多次波从叠前数据中减去。

第 4 步, 虚同相轴法预测和压制层间多次波是自上而下进行的, 即先去除2有关的层间多次波, 再针对地层3重复第 1～3 步, 预测并去除与3有关的层间多次波, 再针对4,5, …, 直到所有的层间多次波都被压制。

利用合成数据验证虚同相轴法预测层间多次波的有效性。图 2 为水平层状速度模型, 密度为 2000kg/m3, 地表为指数吸收边界, 因此该模型不产生自由表面多次波, 通过声波有限差分正演模拟得到合成地震资料。图 3 展示应用虚同相轴法的结果, 可以看到能量较强的层间多次波都被很好地压制, 且没有损伤有效波信号。该实例证明了虚同相轴法预测和压制层间多次波的正确性。

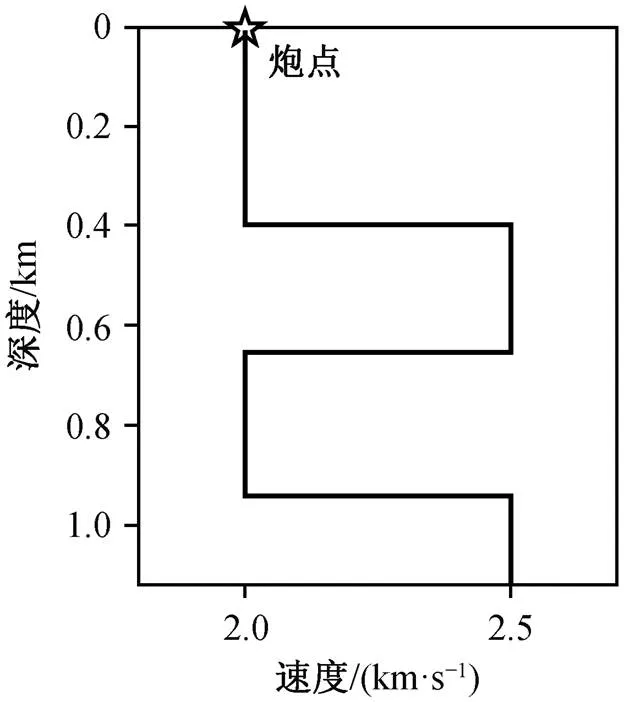
地表为吸收边界, 炮点和检波点均位于地表

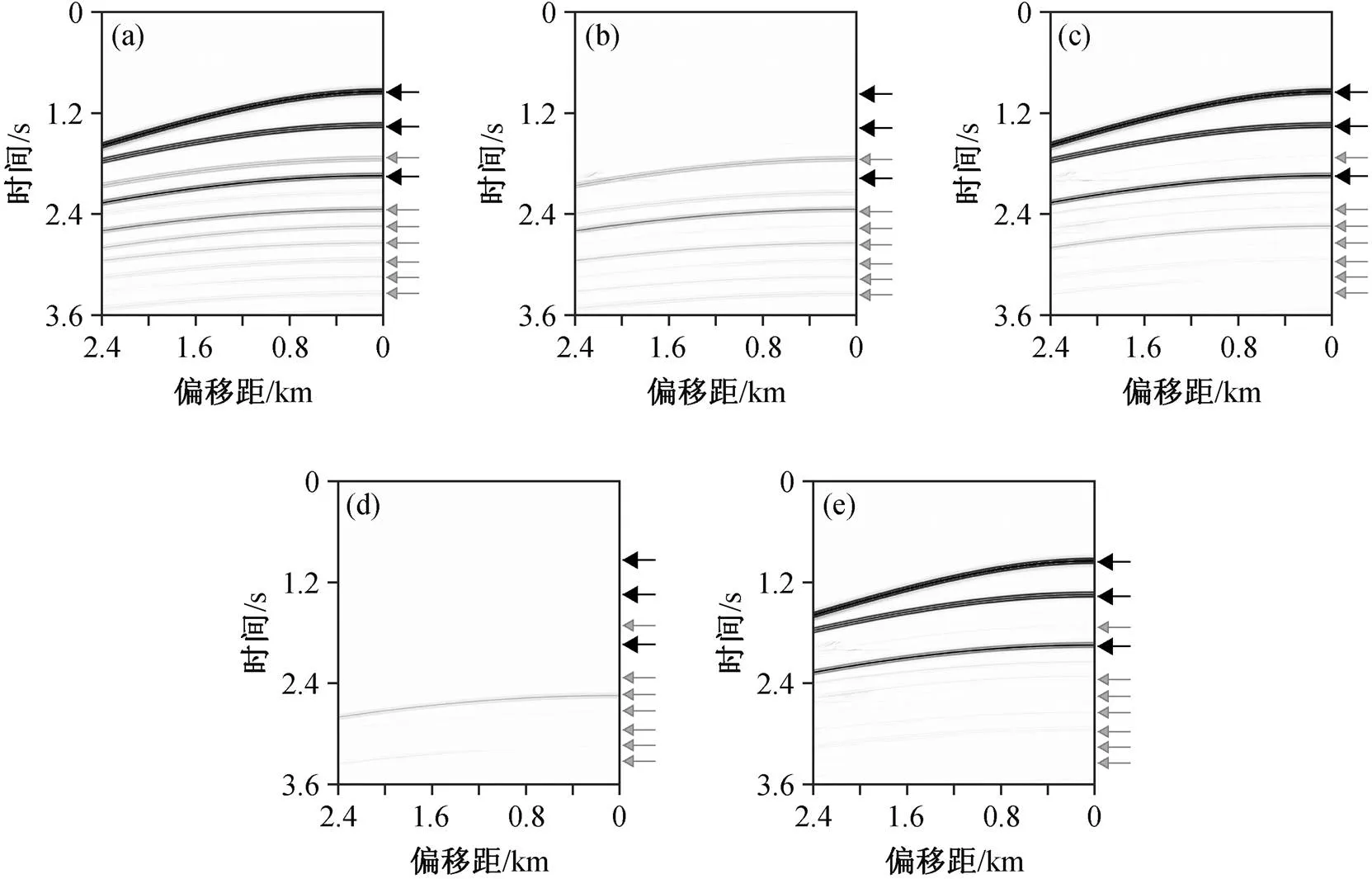
(a)为原始数据, 已切除直达波; (b)为预测的与第1层反射界面有关的层间多次波; (c)为自适应相减(b)中层间多次波的结果; (d)为预测的与第2层反射界面有关的层间多次波; (e)为自适应相减(d)中层间多次波的结果。合成数据通过图2模型的正演得到, 黑色箭头指示一次反射波, 灰色箭头指示层间多次波

当常规的虚同相轴法应用于炮点域或检波点域的数据中, 在计算两点间的地震波信号时, 需要使该两点周围炮检点的地震数据参与积分运算, 要求炮检点的分布相对规则且足够密集, 以便保证积分精度[10,14]。对于二维或三维的数据处理, 这样做会产生巨大的运算量, 并且中国西部地区的复杂地表结构难以保证规则且密集的炮检点分布。为解决这些问题, 本文对方法做以下两点改进。

1)在叠前 CMP‒偏移距域中, 对经过精确动校正的数据逐道应用虚同相轴方法预测层间多次波。由于动校正将各观测点的旅行时修正为各点的法向反射时间, 即 CMP‒偏移距域中的每道记录都成为自激自收的地震记录, 相当于将二维和三维数据降成一维数据, 大大减少后续运算量。应用虚同相轴法, 一维数据(即单道数据)仅需要自身数据就可以预测层间多次波, 不需要周围炮检点的地震道参与积分运算, 因此不再要求炮检点密集而规则地分布。另外, 该方法处理的是叠前地震资料, 能够更好地改善速度分析、叠前属性分析和叠前偏移的效果, 具有比叠后资料的多次波压制更大的价值。

2)引入加权叠加的参考道, 参与虚同相轴法的互相关和褶积运算, 提高预测层间多次波的精度。虚同相轴法中的互相关和褶积容易受数据噪声影响, 而叠前陆地地震资料的信噪比往往较低, 单道数据应用虚同相轴法难以保证好的预测和压制效果。本文方法对叠前 CMP 道集进行加权叠加, 得到高信噪比参考道, 将该参考道与叠前 CMP 道集做互相关, 构建虚同相轴记录, 再将虚同相轴记录与叠前 CMP 道集进行褶积, 预测层间多次波。

引入加权叠加的目的是, 减小误差较大道集在叠加中的权重, 提高叠加参考道的信噪比, 加权叠加的计算公式[16]如下:

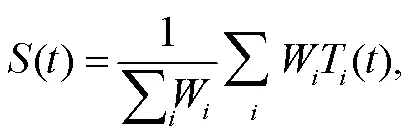
其中,T()为叠前 CMP 道集中的第道,为旅行时,W为第道记录的权重函数,()为加权叠加得到的参考道。权重函数W由相似度确定:

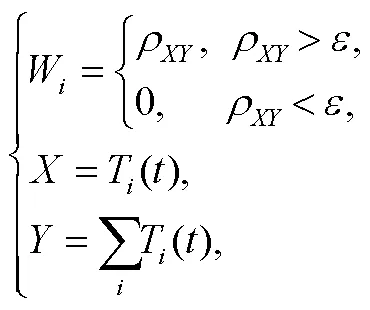
应用本研究改进的方法预测层间多次波的过程如下。

1)将经过精确动校正后的数据重排至 CMP‒偏移距域, 获得叠前 CMP 道集。

2)构建参考道: 对叠前 CMP 道集进行加权叠加, 得到高信噪比参考道。

3)将虚同相轴法应用于经过精确动校正的叠前 CMP 道集, 实现过程如下。

①数据切割: 记来自地层的反射波旅行时为t, 将参考道切割成仅包含来自地层的反射波数据upper()和旅行时大于t的数据lower()。对叠前CMP 道集做同样的切割, 即切割成仅包含来自地层的反射波数据upper()和旅行时大于t的数据lower()。

②在叠前 CMP 道集中, 将upper()与每道的upper()做互相关, 构建虚同相轴数据vir(), 互相关计算公式如下:

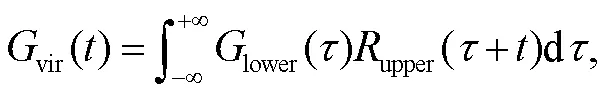
其中,表示时间,表示积分自变量时间。

③将vir()与lower()褶积, 预测与地层1有关的层间多次波, 褶积式如下:

其中,IM()为预测的层间多次波。

引入加权叠加的参考道, 不影响后续互相关和褶积的计算精度。原因是, 用于加权叠加的是经过精细动校正的道集, 被“校平”的地震同相轴可实现同相位叠加, 因此基本上保留了原始信号的相位和位置信息。振幅经过叠加后会发生改变, 但本文方法在预测层间多次波后, 进行最小二乘匹配, 可以避免预测信号与原始道集信号的振幅和相位不匹配问题。

2 应用实例

选择中国西部某工区陆地地震实际资料, 应用本文方法压制层间多次波。经过动校正的叠前 CMP道集(图 4(a))中, 一次波和多次波的位置是根据该工区的地震波速度模型反推得到的。使用常用的商业软件 Radon 变换压制层间多次波。由于层间多次波与一次反射波的视速度和频率很接近, 在 Radon域、-域和-域中均难以有效地将两者分离。如图 4(b)所示, 虽然层间多次波被压制, 但一次反射波同时被压制, 损伤了有效信号, 不利于后续成像显示和构造解释。使用本文方法预测的多次波结果(图 4(c))显示, 在椭圆所示区域均能够较好地预测多次波, 经过自适应相减而去除多次波后的结果(图 4(d))中, 虚线椭圆指示的层间多次波得到有效的压制, 而实线椭圆中混叠的多次波被压制, 两组一次反射波很好地突显出来。

(a)为经过动校正的原始CMP道集; (b)为Radon变换压制多次波的结果; (c)和(d)分别为本文方法预测的多次波和压制多次波后的结果。虚线椭圆标示多次波发育的位置, 实线椭圆标示一次反射波和层间多次波混叠的位置

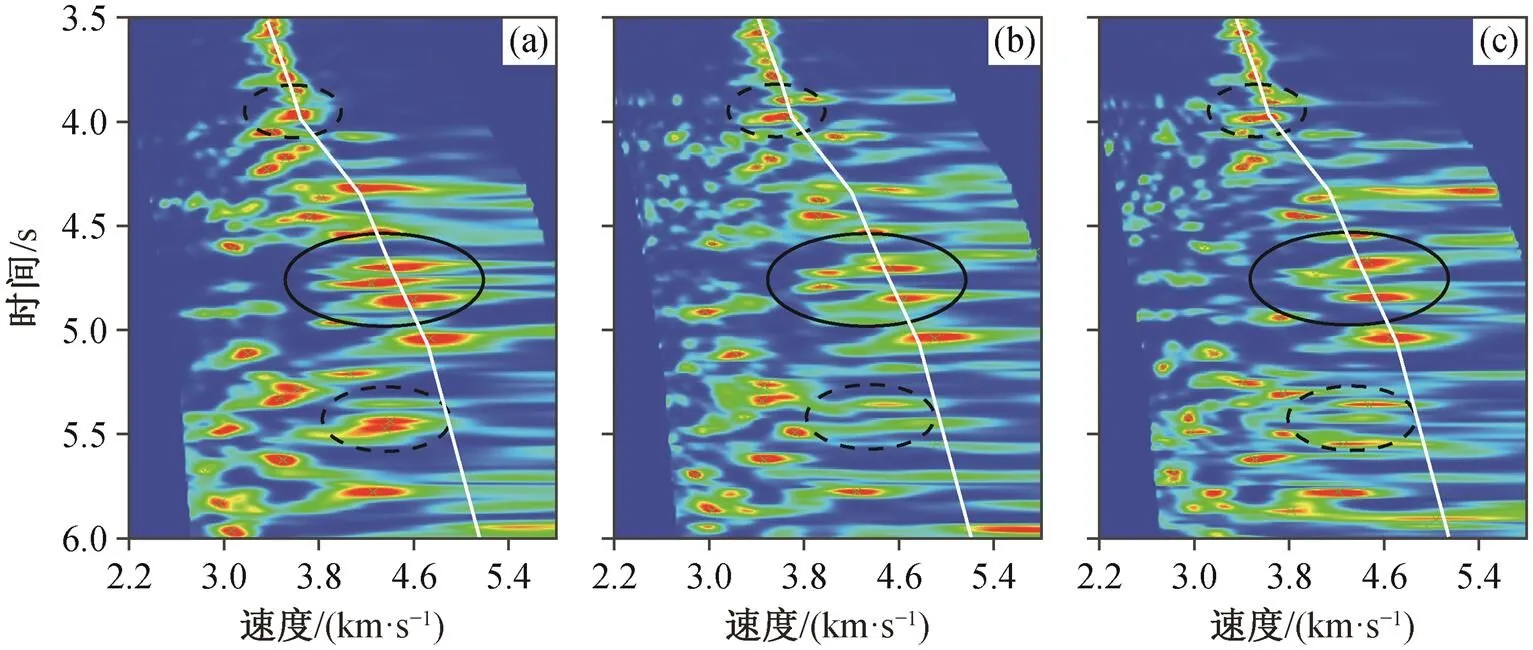
(a)未压制多次波; (b)Radon变换结果; (c)本文方法结果。实(虚)线椭圆标示的区域与图4中实(虚)线椭圆标示的区域一一对应, 白线为拾取速度的位置; 颜色变化体现地震同相轴叠加后的能量强弱, 从红色到蓝色表示能量从强变弱, 能量较强的位置可能指示地层的叠加速度

图 5 为图 4 中 CMP 道集对应的叠加速度谱。图5(a)中, 4.8s 处一次波和多次波混叠的位置(实线椭圆), 上下两个能量团对应一次波, 而中间的能量团对应多次波, 多次波的视速度略低于一次波, 因此通过 Radon 变换等传统滤波类方法去除多次波的同时, 难免损伤一次波。图 5(b)中, 经过 Radon 变换, 虽然多次波的能量团被压制, 但一次波对应的上下两个能量团也在一定程度上受到损伤, 能量团左侧部分被明显压制, 能量团中心向右侧偏移。图 5(c)中, 采用本文方法, 多次波的能量团被很好地压制, 同时一次波的能量团得到较好的保留, 能量团的中心并未漂移。另外, 4.0 和 5.5s 处的多次波能量团, 其视速度与一次波相差较多, 因此 Radon 变换和本文方法均可以有效地压制该多次波, 甚至 5.5s 处Radon 变换压制多次波更彻底, 而本文方法有少量能量团残留, 但两者在叠后剖面上的差异不明显(图 6(c)和(e)中 5.5 s, 4.0～4.5km 处), 主要因为动校正是根据拾取速度进行的, 即偏离拾取速度的同相轴无法“校平”, 5.5s 处的能量团偏离拾取速度(图 5中白线所示)较多, 其对应的同相轴无法“校平”, 因此在叠加时无法实现同相位叠加, 被相对压制。

从图 6 可以看到, 叠加剖面中存在两组明显的强反射层, 在这两组强反射层之间容易产生层间多次波。在两组强反射层同相轴的下方, 出现明显的“窜层”现象(图 6(a)), 会影响后续剖面解释的精度。用 Radon 变换压制层间多次波的效果不佳(图6(c)), “窜层”现象并未改善, 且强反射层振幅有所减弱, 即损伤了一次反射波, Radon 变换预测的多次波结果(图 6(b))中也包含较多的有效信号。应用本文方法很好地压制了层间多次波(图 6(e)), “窜层”现象几乎消失, 强反射层同相轴的连续性得到改善, 并且本文方法预测的层间多次波(图 6(d))中几乎不包含强反射层同相轴的信号, 对有效信号起到很好的保护作用。

3 结论与讨论

本文提出降维的虚同相轴法, 实现叠前陆地地震资料的层间多次波压制。与传统的虚同相轴法相比, 本文方法实现变相的降维处理, 大大减低运算量, 同时引入加权叠加的高信噪比参考道集, 保证单道数据应用虚同相轴法的预测精度。将本文方法应用于中国西部某工区陆地地震实际资料的多次波压制, 取得明显的效果, 展现了本文方法对陆地层间多次波压制问题的理论意义和应用前景。

本文方法是对目前主流的基于共中心点叠加方法的处理流程中多次波压制环节的改进, 因此适用范围与共中心点叠加方法一致。虽然共中心点叠加方法是基于地下为水平层状结构的假设, 但依然适用于大部分地震资料的处理。然而, 当存在严重的非水平结构(如垂向的盐丘体)或横向非均匀性强烈的地下结构(如极其破碎的近地表以及复杂溶洞结构等)时, 共中心点叠加方法难以获得满意的叠加剖面。

本文方法应用效果的关键是精细的叠前处理。一是叠前去噪, 比如压制陆地资料中的强频散面波后, 一般都有面波残留(因为完全压制面波会损伤有效信号), 会明显地降低深部叠前道集的信噪比; 如果叠前去噪不完善, 可能残留野外噪声、外源噪声和表面多次波, 这些噪声都会影响叠前单道应用虚同相轴法预测层间多次波的精度。二是精细的动校正, 必须保证可以近似地将叠前单道包含的地震记录视为沿法向自激自收的地震记录, 才能保证层间多次波的预测精度。“层间多次波压制→改善速度谱→提高速度拾取精度→提高动校正精度→提高层间多次波预测和压制效果”可循环进行, 直到处理效果不再改善为止。当连续两次的速度谱能量团变化不大时, 即可认为处理效果不再改善。一般情况下, 1～2次循环即可。

后续工作中, 拟进一步增强本文方法的普适性, 包括提高方法的抗噪性和提高对动校正误差的容错空间。

[1]Yilmaz Ö.Seismic data analysis: processing, inver-sion, and interpretation of seismic data.2nd ed.Tulsa: Society of Exploration Geophysicists, 2001

[2]Verschuur D J.Seismic multiple removal techniques — past, present and future (revised edition).DB Hou-ten: European Association of Geoscientists & Engi-neers, 2013

[3]张广利, 郝重涛, 姚陈.海洋地震资料多次波衰减方法综述.地球物理学进展, 2016, 31(6): 2777–2787

[4]赵昌垒, 叶月明, 姚根顺, 等.线性拉东域预测反褶积在海洋多次波去除中的应用.地球物理学进展, 2013, 28(2): 1026–1032

[5]胡天跃, 王润秋, 温书亮.用聚束滤波方法消除南海地震资料中的多次波.石油地球物理勘探, 2002, 37(6): 18–23

[6]刘语, 刘建红, 刘国峰, 等.陆上地震资料多次波识别与压制技术.石油地球物理勘探, 2018, 53(增刊1): 24–28

[7]匡伟康, 胡天跃, 段文胜, 等.基于自适应变步长波场延拓的可控层分阶层间多次波模拟.地球物理学报, 2020, 63(5): 2043–2055

[8]Verschuur D J, Kelamis P G.Surface-related multiple elimination on 3D land data // SEG Technical Pro-gram Expanded Abstracts.Dallas, 1997: 1383–1386

[9]叶月明, 郭庆新, 庄锡进, 等.不同阶次自由表面相关多次波预测与成像方法.地球物理学报, 2019, 62(6): 2237–2248

[10]Ikelle L T.A construct of internal multiples from surface data only: the concept of virtual seismic events.Geophysical Journal International, 2006, 164 (2): 383–393

[11]刘嘉辉, 胡天跃, 彭更新.自适应虚同相轴方法压制地震层间多次波.地球物理学报, 2018, 61(3): 1196–1210

[12]谢越越, 胡天跃.1.5维逆散射级数法消除海上地震勘探资料中的鬼波.北京大学学报(自然科学版), 2018, 54(3): 80–90

[13]Zhang L, Slob E.Marchenko multiple elimination of a laboratory example.Geophysical Journal International, 2020, 221(2): 1138–1144

[14]Ikelle L T, Erez I, Yang X.Scattering diagrams in seismic imaging: more insights into the construction of virtual events and internal multiples.Journal of Applied Geophysics, 2009, 67(2): 150–170

[15]吴静, 吴志强, 胡天跃, 等.基于构建虚同相轴压制地震层间多次波.地球物理学报, 2013, 56(3): 985–994

[16]吕雪梅, 安圣培, 胡天跃, 等.相似度加权的超虚干涉法加强初至波信号.北京大学学报(自然科学版), 2018, 54(1): 87–93

Dimensionality Reduced Virtual Event Method to Suppress Internal Multiples for Land Seismic Data

XIE Fei1, AN Shengpei1, ZHU Chenghong1, LIU Jiahui2, HU Tianyue2,†

1.Petroleum Exploration and Production Research Institute, Sinopec, Beijing 100083; 2.School of Earth and Space Sciences,Peking University, Beijing 100871; † Corresponding author, E-mail: tianyue@pku.edu.cn

As the land internal multiples could not been obviously attenuated, theauthors develop the dimensionality reduced virtual event method to suppress the internal multiples in pre-stack land seismic data.Compared with the traditional virtual event method, the authors apply the virtual event method trace by trace on the pre-stack gathers after accurate dynamic correction to predict internal multiples.It achieves dimensionality reduction, greatly reduces the amount of calculation, and no longer requires a regular and dense enough distribution.Meanwhile, this method introduces a weighted reference trace with high signal-to-noise ratio to participate in the cross-correlation and convolution operations of the pre-stack gathers, which improves the prediction accuracy of the virtual event method.This method is applied to actual land seismic data in western China and achieved obvious effect when suppressing internal multiples.

internal multiples; virtual event; reduced dimensionality; correlation; adaptive subtraction

10.13209/j.0479-8023.2021.083

2020‒12‒02;

2021‒01‒26

国家重点研发计划(2018YFA0702503)和国家自然科学基金(41674122)资助