基于GRA-LSTM 与SARIMA 组合模型的季节性时间序列预测
2021-12-17罗广诚郜家珏蔡文学
罗广诚,郜家珏,蔡文学
(华南理工大学 电子商务系,广州 510000)
0 引言
时间序列预测是通过历史观测数据建立模型以解释数据变化规律,并对未来进行预测的技术,广泛应用在水文气象、信号处理以及金融经济等许多领域。时间序列数据分为平稳性时间序列和非平稳性时间序列。对于平稳时间序列,尤其是线性模型的建模和预测,已有许多成熟的技术和方法。但在实际问题中,大多数序列并非平稳、线性的,而目前对于这类时间序列的分析和处理上没有较为完善的方法。
随着人工智能技术的发展,神经网络、支持向量机等模型以其良好的非线性预测和实用性,被广泛应用在时间序列预测中。其中长短期记忆网络(Long Short-term Memory,LSTM)是应用最广泛的预测方法之一,主要应用方面有交通流预测、故障时间预测、语义关系分类、文本分类、情感分类、股票预测等方面[1-5]。LSTM 模型是一种时间递归神经网络,对于时间序列的数据而言预测精度高,并且LSTM 模型拥有大量的非线性传输层,不仅可以依据历史数据对未来变化趋势进行预测,还可以通过输入影响因素等非线性数据敏锐捕捉非线性因素影响下的未来变化;基于灰色关联度分析(Grey Relation Analysis,GRA)进行LSTM 模型中非线性输入因素的选择是常用的方式[6]。但其也存在对季节性时间序列中的周期、趋势性变化不敏感的特点[7]。而季节性差分自回归移动平均模型(Seasonal Autoregressive Integrated Moving Average,SARIMA)对于包含周期、趋势性变化的季节性时间序列预测具有良好的效果,目前被广泛应用在城市交通流预测、价格预测、疾病预测、CPI 和GDP指数预测等方面[8-10]。然而SARIMA 模型仅适用于短期线性时间序列的预测并且预测精度较低[11]。
综上所述,若采用组合思想则能够充分利用二者的优势,实现对序列更为准确的预测。针对SARIMA 模型和LSTM 模型的组合,文献[12]中提出将两种模型进行串联组合,将SARIMA 模型预测后的结果作为输入层数据,重新输入到LSTM 模型中,得到最终结果。而本文针对两种模型预测上的优劣势,提出采用并联方式将两种模型进行组合,即将数据分别输入SARIMA 模型与LSTM 模型,然后再对两种预测结果进行合理并联,以实现将SARIMA 对周期、趋势性变化敏感的优点及LSTM预测精度高且可以用来非线性数据进行预测的优点相组合,提高季节性时间序列预测精度。其中GRA-LSTM 模型的输入数据需要基于GRA 法选取关键影响因素作为非线性数据输入。本文以某民航公司春运数据为例,对组合模型进行了验证。结果表明,组合模型的预测精度高于支持向量机、灰色预测、GRA-LSTM 单模型以及SARIMA 单模型。
1 GRA-LSTM 模型
GRA—LSTM 模型是由GRA 和LSTM 模型组合而成,基本原理是先根据GRA 法结果,选择相关性高的因素作为关键影响因素,然后将其作为非线性输入量输入到LSTM 模型中进行预测。
1.1 GRA法
GRA 法是一种基于各影响因素数据分析,用灰色关联度来描述因素间关系的多因素统计分析方法。GRA 法原理简单,不需要大量数据作为基础,计算量小、运行速度快,适用于分析各种影响因素与客流量之间存在的相关关系。因此,采用GRA 法求得各影响因素与民航客流量之间序列变化趋势的相似或相异程度,从而删选出影响民航客流量的关键影响因素,并作为LSTM 模型的输入进行预测。
灰色关联度分析法具体步骤如下:
(1)确定反映系统行为特征的参考序列X0;影响系统行为的比较序列X1,X2,...,Xn;其中Xi={Xi(k)|k=1,2,...,m}。
(2)对参考序列和比较序列进行无量纲化处理:

其中,ρ为分辨系数,取值区间为(0,1),具体取值视情况而定,ρ值越小,分辨力越大。当ρ≤0.546 3时,分辨力最好,通常取ρ=0.5。
(4)计算X0序列和Xi序列的关联度ri:
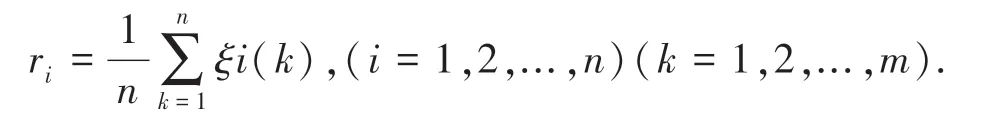
基于GRA 法分析结果,对灰色关联度ri=1,2,...,p按从大到小进行排序。若设灰色关联序列为r1>r2>...>rp,则表明第一个比较序列对应的影响因素对参考序列影响最大,第p个因素影响最小。对设定的最小关联度阈值σ,取σ∈(0,1),对满足ri <σ的比较序列则认为这些序列对网络输出的影响较小,将其删除从而优化输入数据,将余下的比较序列对应的影响因素作为关键影响因素输入到LSTM 模型中。
1.2 LSTM 模型
LSTM 深度神经网络通过复杂的非线性单元构建,具有长期记忆效应和深度学习能力。LSTM 网络由1 个输入层、1 个输出层以及多个隐藏层构成。其中隐藏层由记忆元组组成,每个元组包含输入门、遗忘门和输出门,门控制着元组和网络之间的信息流动,其基本结构如图1 所示。
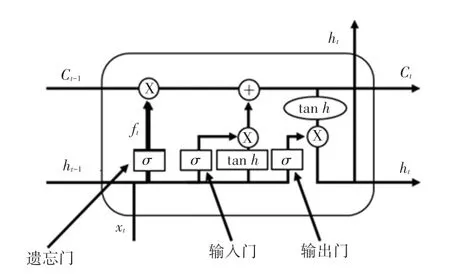
图1 LSTM 网络元组结构Fig.1 Tuple structure of LSTM network
图1 中,Ct-1和Ct表示细胞的旧状态和新状态,细胞状态是LSTM 网络的关键,像传送带一样在整个链上运行。在LSTM 中,门结构可以决定信息是否通过,以对细胞状态信息有选择地进行增删。其主要计算步骤如下:
第一步:用来决定什么信息可以通过,即遗忘门。其中,输入为当前层的输入xt和上一层的输出ht-1,遗忘门状态输出ft为:

第二步:产生需要更新的新信息并存储于细胞状态中,即输入门。新的细胞状态Ct首先通过旧的细胞状态Ct-1乘以ft来忘记不需要的信息,然后加上新的候选信息it·。其中,it为输入门状态。
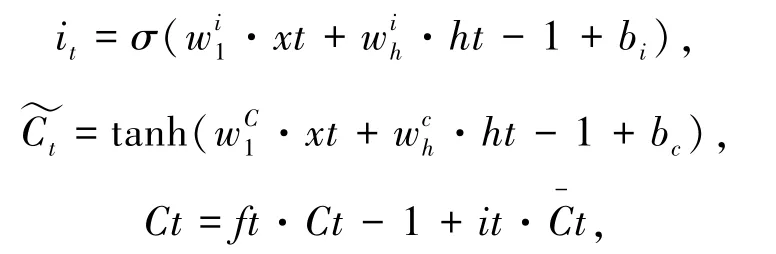
第三步:输出门用来决定模型的输出。首先,通过sigmoid 层得到初始输出状态值ot后,使用tanh层将细胞状态的值缩放到[-1,1]之间,相乘得到输出值ht。

其中,ft、it、ot分别表征遗忘门、输入门和输出门的状态值;为沟通输入xt与元组的遗忘门、输入门、输出门以及元组输入的权重矩阵;为连接上一层输出ht-1与元组的遗忘门、输入门和输出门以及元组输入的权重矩阵;bf、bi、bo、bc为遗忘门、输入门、输出门和元组输入的偏置向量;σ为sigmoid激活函数。
1.3 GRA-LSTM 模型预测流程
首先,根据GRA法的分析结果选择合适的影响因素作为关键影响因素,然后对历史客流量数据和关键影响因素数据进行归一化处理后,构成输入量输入到LSTM网络模型中。PCA-LSTM预测模型的表达式如下:
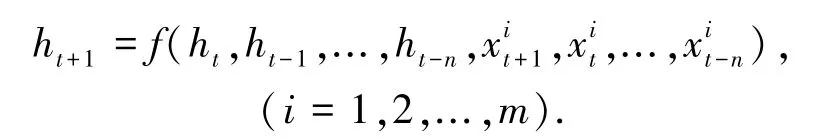
其中,ht+1为预测值;ht,ht-1,...,ht-n是历史数据;是通过GRA法选出的m个关键影响因素数据。其中包括历史数据及预测值ht+1对应的当前输入值。根据设定目标误差不断训练模型,直至误差小于目标误差,此时输出预测结果。
2 SARIMA 模型
SARIMA模型又称季节性差分自回归滑动平均模型,是在ARIMA模型的基础上演化出的一种针对具有季节性或周期性规律变化数据的预测模型,是时间序列预测领域中的主要预测模型之一。该模型的通用表达式为:
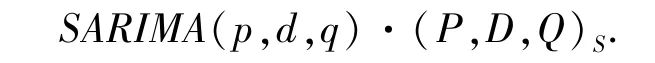
其中,p为自回归阶数;q为移动平均阶数;d为差分阶数;P、Q、D分别为季节求和自回归移动平均模型中的自回归、移动平均和差分的值;S为季节周期和循环长度。
SARIMA模型的主要处理步骤为:
(1)判定数据平稳性
首先将初始数据进行预处理,对处理后的数据构造时间序列折线图进行可视化,通过观察折线图对数据的平稳性进行初步判断。
(2)数据差分
若初步判定为非平稳数据,则需要对数据进行差分,不断进行差分操作直到数据变为平稳时间序列。
(3)通过ACF(自相关函数)和PACF(偏自相关函数)图形确定参数值引入ACF和PACF图形,通过判断可视化的图形是截尾还是拖尾来确定模型参数中p、P、q和Q的值。判定规则如下:若ACF拖尾且PACF截尾,通过可视化的阶数确定p和P;若ACF截尾且PACF拖尾,通过可视化阶数确定q和Q;若ACF和PACF均为拖尾,则通过可视化阶数可以确定p和P、q和Q。
(4)确定S值
通过对季节性时间序列数据进行平均法、移动平均趋势剔除法等方法分解来确定S的值。
(5)模型确定
得到所有参数后,需要使用参数估计对模型进行校验,直至确定最终模型。
3 组合模型设计
组合模型是在SARIMA和LSTM单模型预测结果的基础上设计了组合层,即基于SARIMA模型预测结果中提取的包含周期、趋势信息的单位节点比例序列,对LSTM得到的初步预测结果进行修正得到最终预测结果,实现了将SARIMA对周期、趋势性变化敏感的优点及LSTM预测精度高且可以用来对非线性数据进行预测的优点相结合。设计思路为:
(1)LSTM单模型预测
将历史数据以及根据GRA法确定的关键影响因素数据输入LSTM模型,得到初步预测结果Li(i=1,2,...,n)。其中,n为最小时间节点个数。
(2)SARIMA单模型预测
将历史数据输入到SARIMA模型得到预测结果Si(i=1,2,...,n)。
(3)组合设计
根据SARIMA模型中的预测结果si抽取包含周期、趋势信息的单位节点比例序列θi,对LSTM得到的初步预测结果进行修正以得到最终预测结果。
①首先根据LSTM模型初步预测结果,得到总时段预测结果数值总和L总:
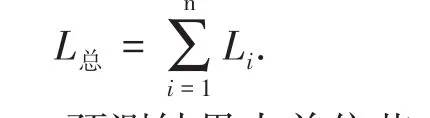
②提取SARIMA预测结果中单位节点Si比例序列θi(i=1,2,...,n),以抽取时间序列中周期、趋势信息,具体计算公式如下:
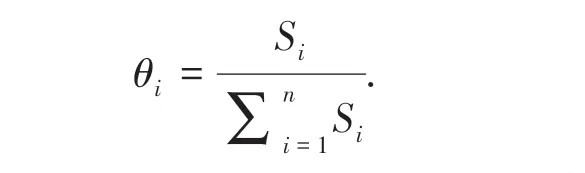
③将SARIMA模型中的单位节点比例序列θi与总时段预测结果数值总和L总相乘,得到最终预测结果fi(i=1,2,...,n)。计算公式为:
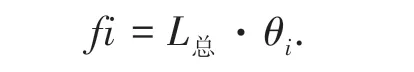
通过组合使得预测结果既可以很好地拟合时间序列中的周期、趋势性变化,也可以敏锐捕捉非线性因素影响下的变化。fi的完整表达式为:

组合模型处理步骤如图2 所示。
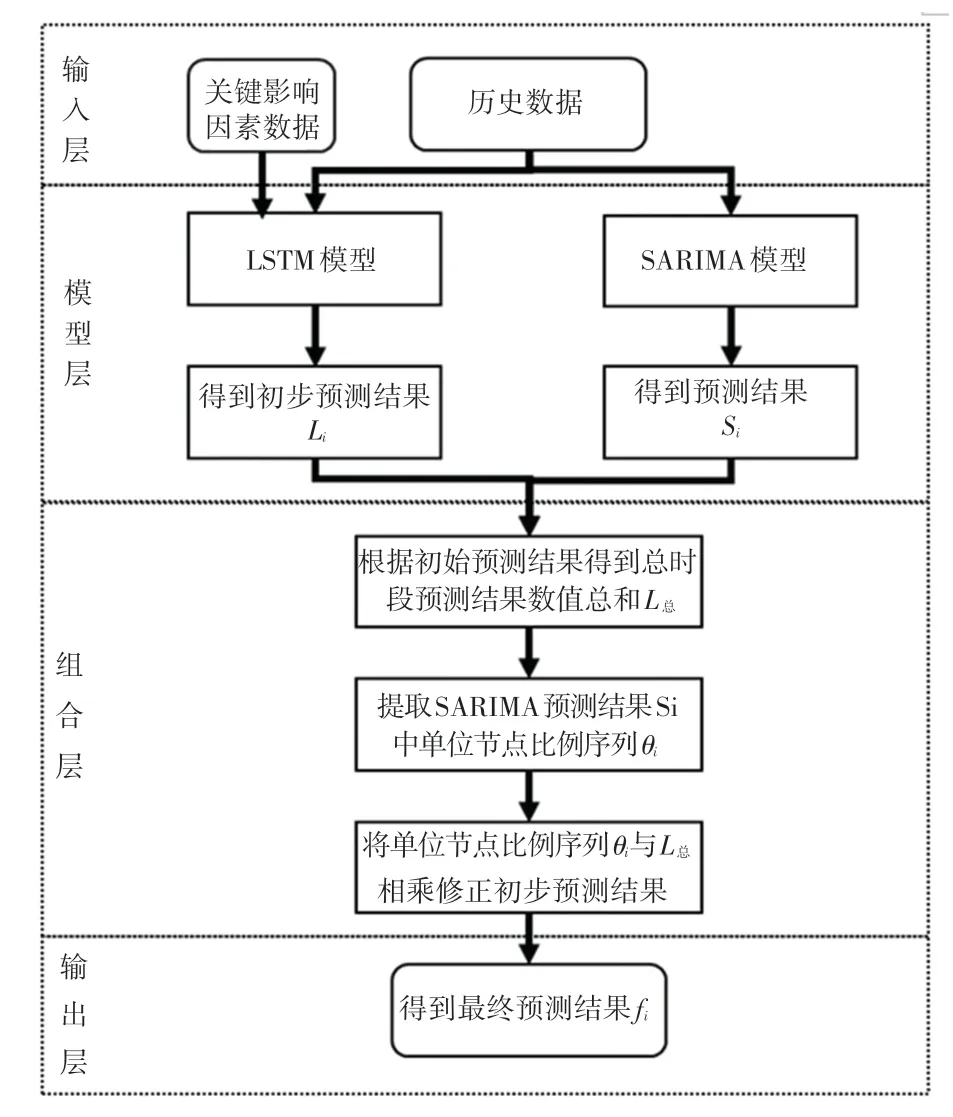
图2 组合模型处理步骤Fig.2 Processing steps of combined model
4 实例分析
实例以某民航公司2016~2018 年春运客流量数据作为测试数据,用于对模型进行训练;将2019年春运客流量数据作为预测数据判断模型预测准确度。
4.1 基于GRA 法选取客流量关键影响因素
影响客运量的因素多种多样,为了更好地研究客运量的关键影响因素,参考相关文献[13-14],提出以下影响航运客运量因素,见表1。

表1 民航春运客流量影响因素Tab.1 Influencing Factors of Air Spring Festival travel rush Passenger Flow
从统计局官网上收集了2016~2018 年春运典型日民航日出港旅客数以及影响因素数据,对其进行灰色关联度分析后,得到的分析结果见表2。
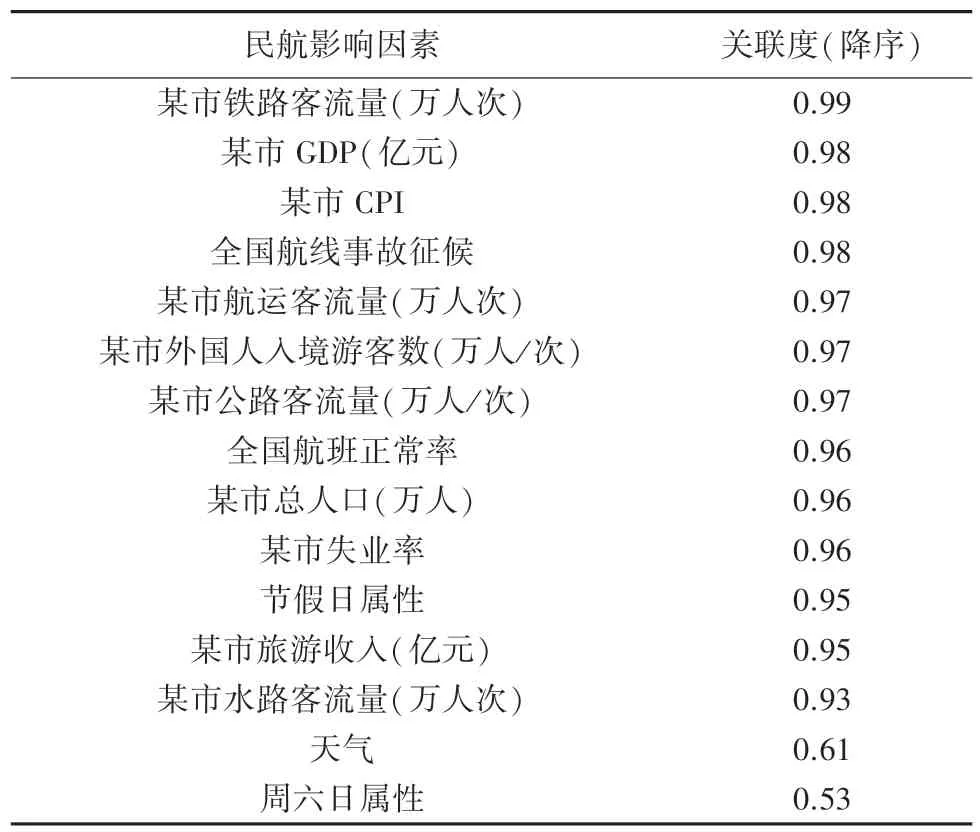
表2 关联度分析结果Tab.2 Correlation Analysis Results
根据关联度分析结果可以得出:
(1)经济社会发展、旅游发展、自身的发展以及其它相关运输方式的发展这4 方面,对航运客流的影响因素均在0.9 以上。
(2)其它因素中,只有节假日属性对航运客流的影响因素大于0.9;天气因素、周六日属性航运客流的影响因素均小于0.7。因此选取影响程度大于0.7 的13 项因素作为关键影响因素。
4.2 模型预测
将2016~2018 年民航春运日出港旅客数以及2016~2019 年关键影响因素数据输入到LSTM 模型中,得到图3 预测结果。

图3 LSTM 单模型预测结果Fig.3 LSTM single model prediction results
由图3 可以看出,LSTM 模型预测结果与真实值拟合度较高,但与真实值相比预测趋势存在延迟。将2016~2018 年民航春运日出港旅客数输入到SARIMA 模型中,得到图4 预测结果:

图4 SARIMA 单模型预测结果Fig.4 Prediction results of single ARIMA model
SARIMA 模型的预测结果在趋势上与真实值基本吻合,但预测精度不甚满意。根据组合模型设计思想,将两种模型进行组合后,得到的预测结果如图5 所示。
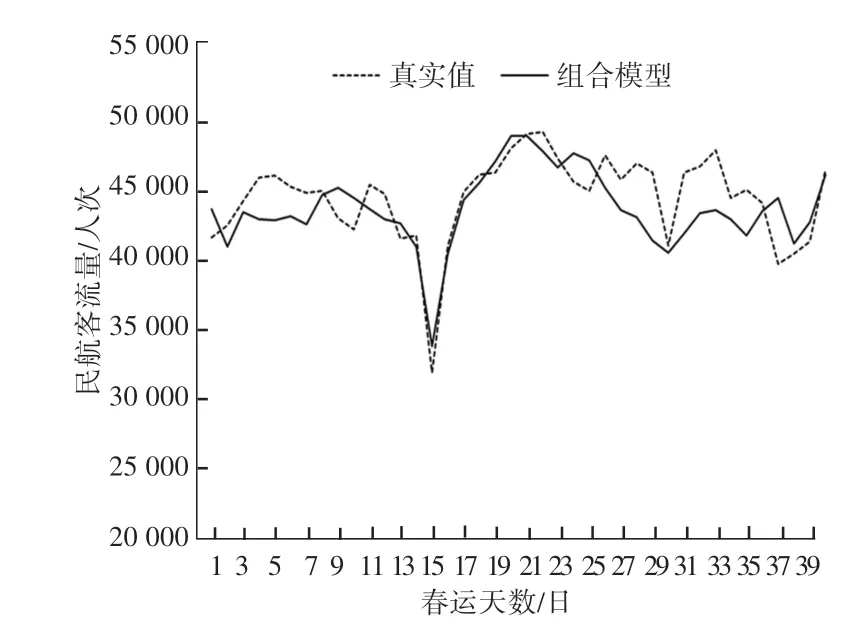
图5 组合模型预测结果Fig.5 Prediction results of combined model
可以看到组合模型无论是在预测精度和趋势变化上都比单模型效果要好。根据表3 可知组合模型预测平均绝对百分比误差为3.9%。

表3 组合模型预测误差Tab.3 Prediction error of hybrid model
4.3 与其它预测模型的对比
为检验和说明组合模型的预测性能,采用支持向量机、灰色预测、GRA-LSTM 单模型以及SARIMA单模型等经典的预测模型与之进行对比,其预测曲线如图6 所示。同时采用MAE(平均绝对误差)、RMSE(均方根误差)以及MAPE(平均绝对百分比误差)作为误差衡量指标,几种模型的预测误差见表4。

图6 几种模型预测结果Fig.6 Prediction results of several models
由表4 和图6 可知,本文提出的GRA-LSTM+SARIMA 组合模型与真实值的拟合程度是最好的,预测误差也是几种模型中最低的。其中,MAPE 比支持向量机、灰色预测、GRA-LSTM 单模型以及SARIMA单模型分别降低了2.1%、1.1%、0.7%、6.7%。

表4 几种模型预测误差Tab.4 Prediction errors of several models
5 结束语
通过评估LSTM 模型和SARIMA 模型的优劣势,提出将两种模型进行组合。通过实验表明,组合模型在预测上比单模型具有优越性。其次组合模型之一的LSTM 模型的输入层不仅仅是历史数据,还有基于GRA 法选取的关键影响因素,因此组合模型能够捕捉非线性时间序列的变化,更好地针对实际变化进行预测。
