基于网络攻击和事件触发的H∞神经网络控制器
2021-12-17陈玲琦高燕马健武燕恬池
陈玲琦,高燕,马健武,燕恬池
(上海工程技术大学 电子电气工程学院,上海 201600)
0 引言
近年来,随着神经网络的发展,各个行业的研究有了新的突破。控制领域的专家充分利用神经网络的自适应性与抗干扰性,将传统控制器与神经网络相结合,使得控制器的性能得到了极大提高。但是数据丢包,网络攻击等现象依然存在。针对上述问题,如何充分利用网络进行数据传输,达到节约网络能量的目的,保证数据的安全性,仍然是个研究的难题。
目前为止,已经发表了许多新的成果来解决网络传输效率的问题。其中,针对有限的带宽传输,提出了一种周期性触发机制[1]。但是进行传输时,会产生大量的冗余信号,造成资源的浪费以及网络传输的拥挤,从而导致网络的性能下降。为了解决这种问题,一种事件触发机制被提出。研究者通过设计函数和阈值,实现对必要的数据进行传输[2]。大大减少了冗余信息的传输,节约了网络资源,网络带宽得到充分利用。基于上述思想,各种控制器开始涌现,例如:利用事件触发机制设计了反馈控制器[3];事件触发机制被应用到模糊神经网络系统中,对事件触发机制的改进也是层出不穷[4]。结合实际场景,本文针对已有的事件触发机制进行了改进,增大了触发间隔,提高了传输效率。
网络传输过程中,网络安全也是一个热点话题,数据的修改或者丢失都可能产生意想不到的后果,造成灾难性的危害,因此研究网络安全刻不容缓。研究网络安全就必须深入理解网络攻击的原理,网络攻击是指利用通信链接并向操作且发送错误的控制信号,一般来说,网络攻击主要包括拒绝服务型攻击和欺骗型攻击。应用满足伯努利的欺骗型攻击,但是如果这种攻击和控制器不匹配,就可能变成阻塞通信通道的干扰信号[5]。针对上述问题,基于动态积分的网络攻击出现,但是很少有文献进行多种攻击相互结合并且作用到神经网络控制器上。
基于上述思考,利用服从伯努利和动态积分的网络攻击并结合改进的事件触发机制构造了H∞神经网络控制器。本文针对每一个传感器,改进事件触发的传输方案来确定本地传输信号,减少了通信资源的消耗。针对累积的动态攻击,本文提出了满足给定约束条件的积分函数;将多时滞增加到系统模型中,构造了新颖的李亚诺普函数。通过上述的约束条件,证明了系统是闭环稳定的且通过LMI 工具箱求解出合适的控制器增益以及触发参数。最后,通过例子说明了其可行性。
1 问题描述
本文应用的时滞网络模型,式(1):
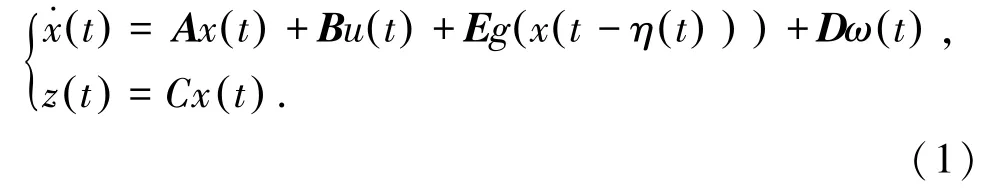
其中,x(t)=[x1(t)x2(t)…xn(t)]为n个神经元的状态变量;u(t)为模型的输入;z(t)为输出变量;g(t)=[g(x1(t))g(x2(t))…g(xn(t))]为网络的激活函数;η(t)为网络延迟的变化且满足0≤η(t)≤ηM;ηM为最大延迟常数;A为对称矩阵;B,C,D,E为适当维度的实数矩阵。
1.1 事件触发机制设计
为了更好的节约网络资源,设计式(2)触发机制[2]:
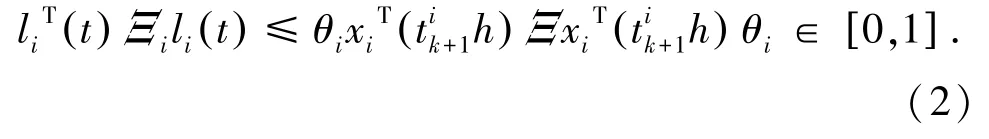
Ξi >0 是一个正定加权矩阵(Ξi=0 变成时间触发器)。事件触发机制有两部分组成:寄存器和比较器。寄存器用来记录最近的采样数据状态x(),设置采样间隔;比较器对当前采样数据的状态x(),判断数据是否满足式(2)触发条件。第i个传感器误差,式(3):
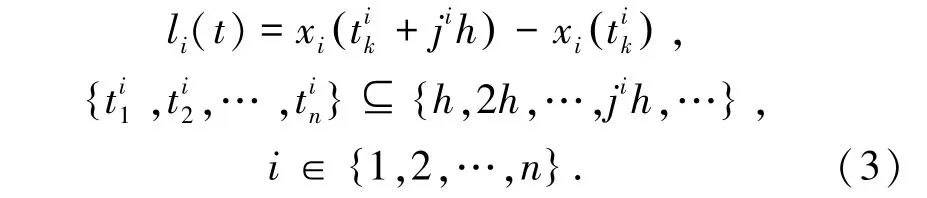

定义:τ(t)=t-tkh-jh可以得到不等式(5):

根据(3)~(5),进而可以确定每一个事件触发器都满足不等式(6):

θ和Ξ都是对角矩阵,分别为:diag{θ1,θ2,…,θn},diag{Ξ1,Ξ2,…,Ξn}。
1.2 网络攻击事件
由于网络传输是很容易遭到攻击进而改变网络传输的信息,本文通过控制输入信号,运用两种攻击方式并结合事件触发得到模型,式(7):
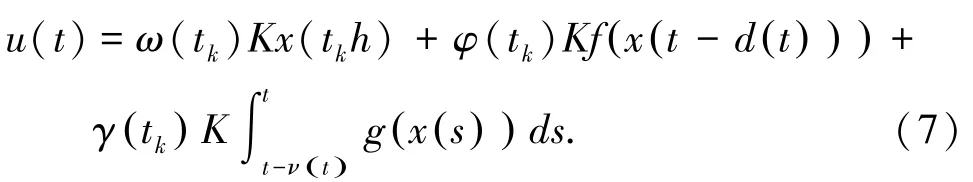
其中:ω(tk)= α(tk),φ(tk)=[1-α(tk)]β(tk),α(t)∈{0,1},β(t)∈{0,1},K表示控制器的增益,f(•)和g(•)表示伯努利攻击函数和动态积分攻击函数,分别如式(8):
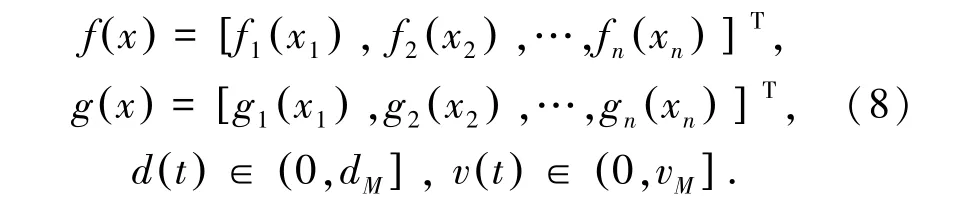
α(tk)=1 意味着网络正常,没有网络的攻击,α(tk)=0,β(tk)=1 发生了伯努利方式的攻击,α(tk)=0,β(tk)=0 发生了积分式的网络攻击。
1.3 相关引理及约束
两种类型的网络攻击函数f(s)和g(x)满足以下条件(9):
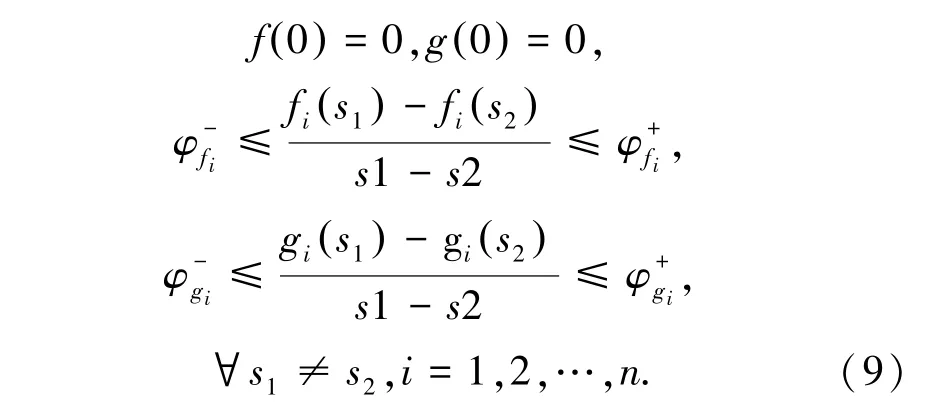
引理1存在对角矩阵vi≥(i=1,2)满足式
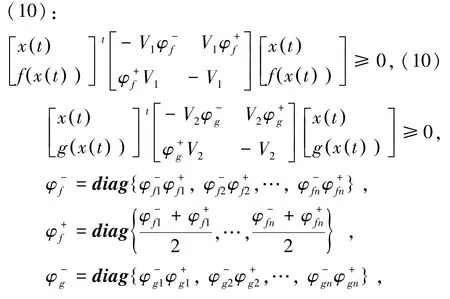

引理4对于列满秩矩阵M,通过奇异值分解得:M=UΣVT,U和V都为正交矩阵,Σ为正实数对角矩阵。如果存在P且P=Udiag{P1,P2}UT,就一定存在一个常数矩阵X,使得PM=MX成立,且存在X满足PBK=BXK,且令Y=XK。
2 建立模型
随机产生的网络攻击可能影响事件触发的条件,进而造成控制器做出错误的判断。因此结合公式(1)和(7),获得控制模型,式(13):
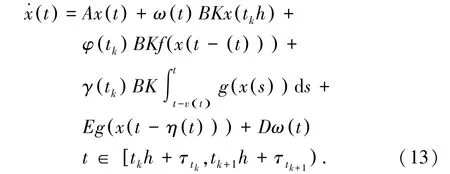
考虑τ(t)的定义以及α(t)∈{0,1},β(t)∈{0,1},可以在(13)的基础上重写模型,式(14):
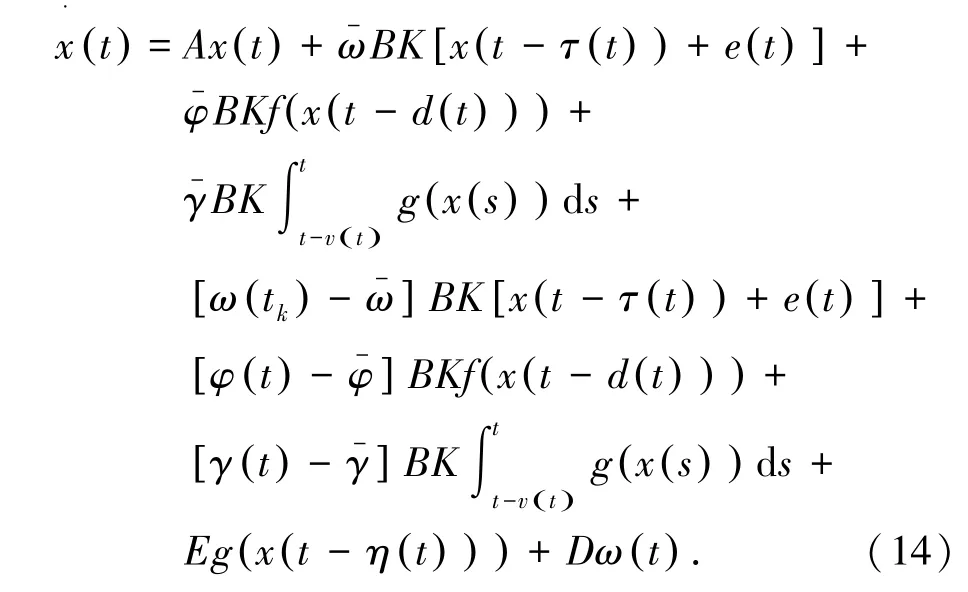
3 主要结果
应用LMI 工具箱,结合以上引理,进而获得充分条件确保了闭环系统(14)的渐近稳定性。
定理已知τM,vM,dM,θ,α,β,如果存在正定矩阵P,R1,R2,R3,Q1,Q2,Q3;适当维度的M1,M2,M3;对角矩阵Ξ,V1,U1,U2以及矩阵Y,则闭环系统(14)是渐近稳定的。

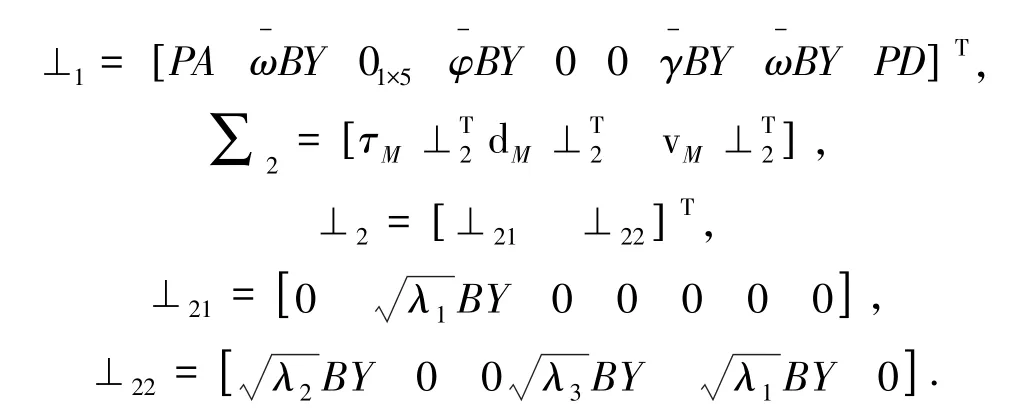
证明针对闭环系统(14),构造了新颖的李雅诺普函数(17):
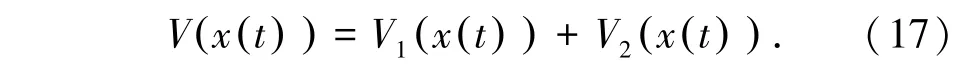
其中,V1(•)和V2(•)分别表示为式(18):
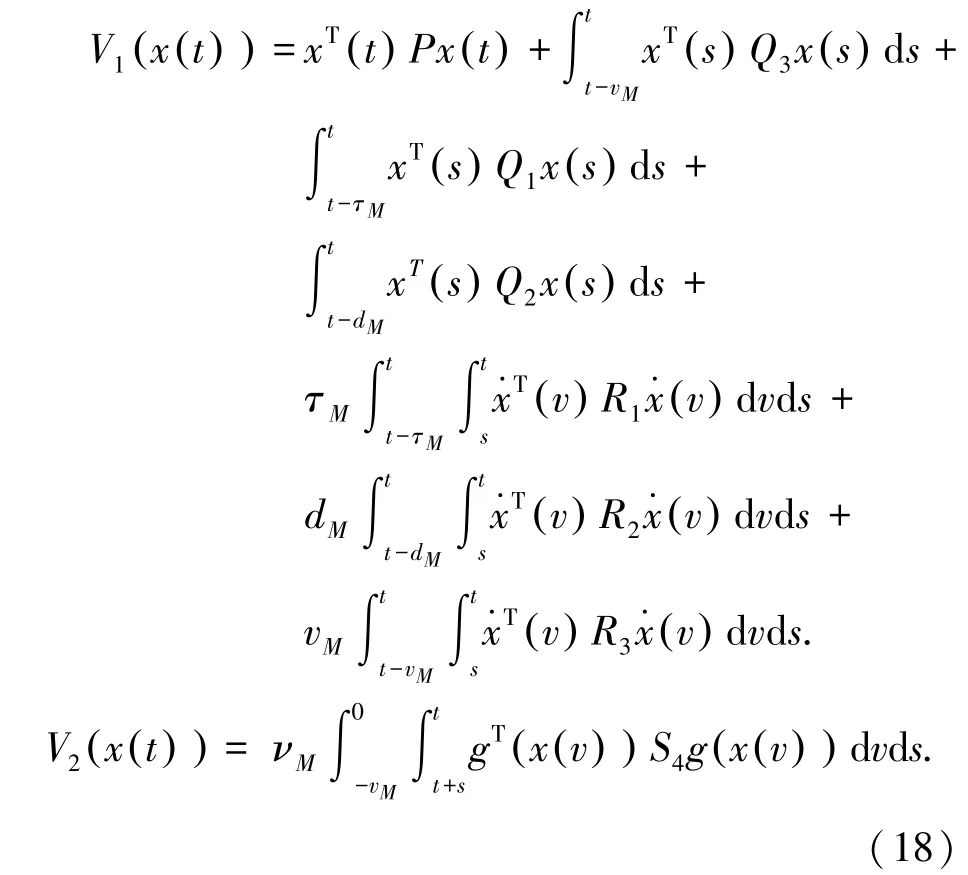
沿着时间轨迹t对v(x(t))的导数求期望,式(19):

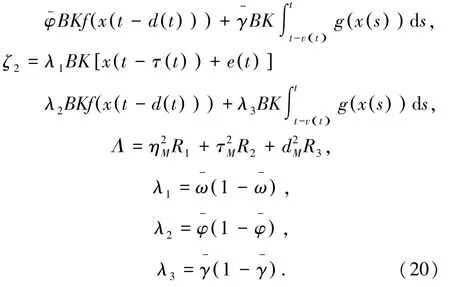
通过引理1,可以对攻击网络函数f(·)和g(·)进行约束,式(21):
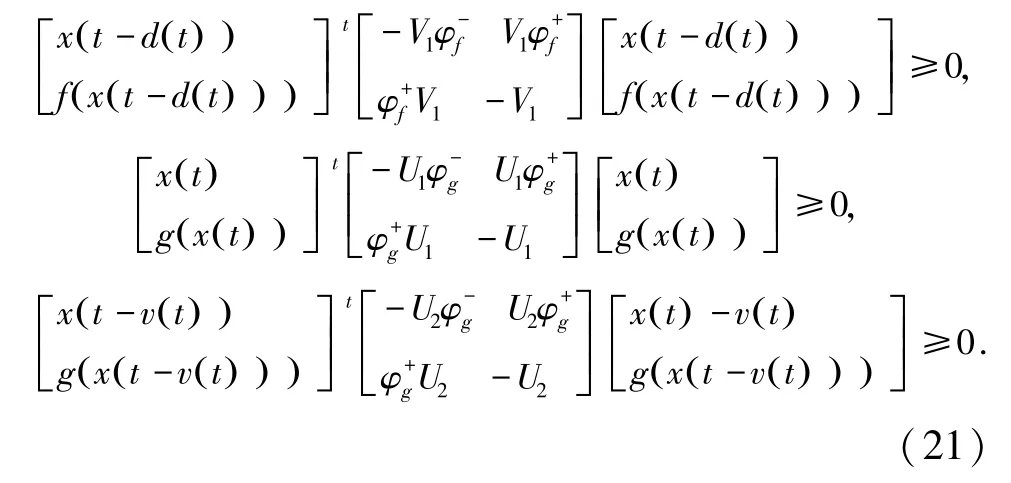
如果存在Ma(a=1,2,3)满足(10),根据引理2可以获得不等式(22):

结合(2),(17)~(20)以及引理3,引理4 可以推出结论,式(23):
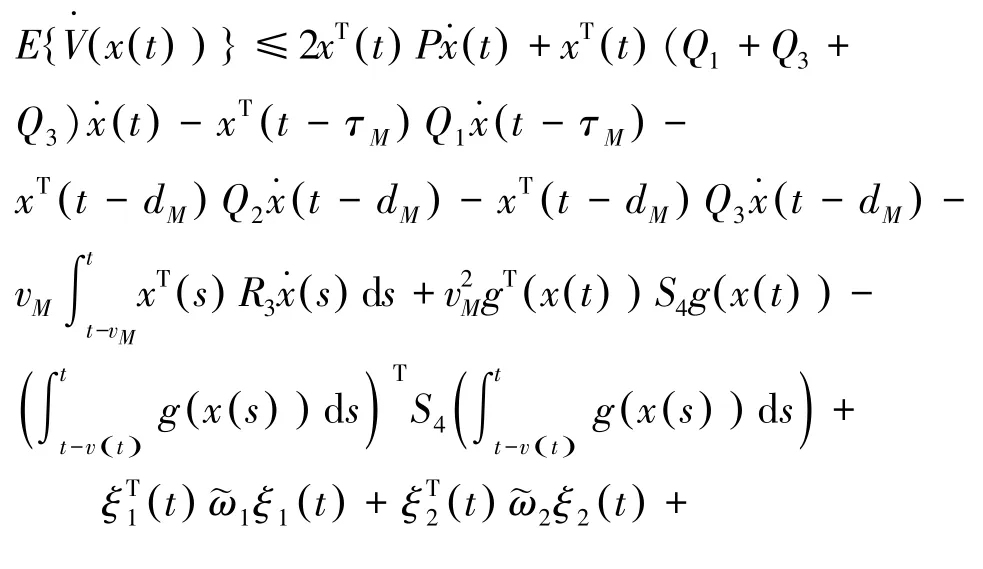
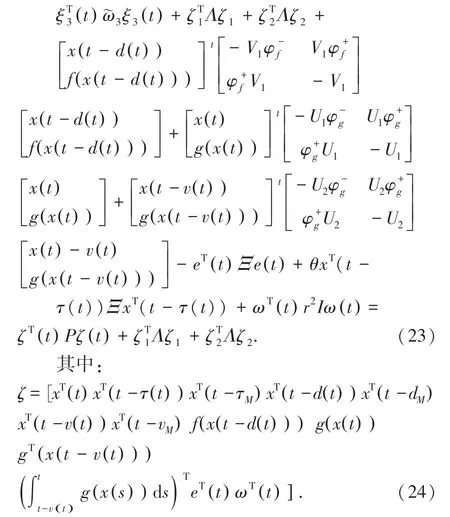
由Schur 定理可以得到(15),即式(25):
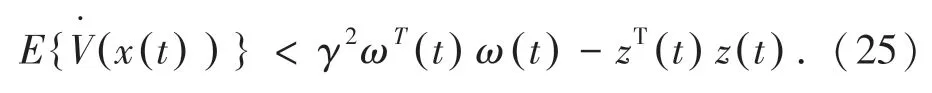
定理证明完毕。
4 数值仿真
用例子(26)对上述理论进行了验证,证明本文控制器的优越性。

仅仅考虑了网络攻击函数f(·),主要基于伯努利分布进行随机改变控制器的输入信号,达到网络攻击的目的[2],正是本文α(tk)=0,β(tk)=1 的情况。而本文采用了两种随机攻击,并且获得了触发器触发情况和控制器响应的实验结果。
根据给定的数值,可以获得如下约束:
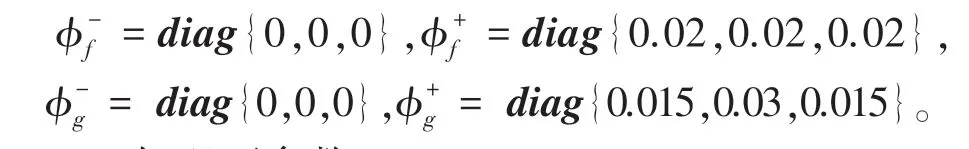
已知以下参数:
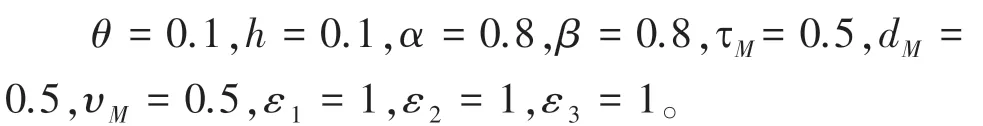
将其带入本文控制器(15)中,利用LMI 工具箱,获得控制器增益,进而得到事件触发矩阵(27):

根据控制器增益,可以分别得到各个传感器的触发情况,如图1~图3 所示。

图1 传感器1 的触发和释放Fig.1 Trigger and release of sensor 1
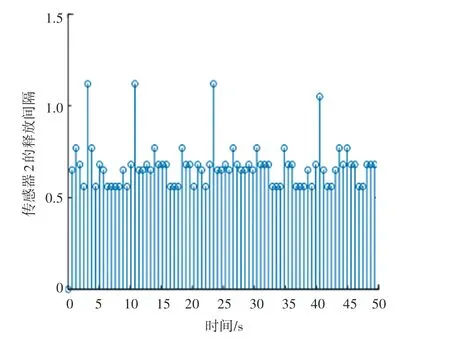
图2 传感器2 的触发和释放Fig.2 Trigger and release of sensor 2
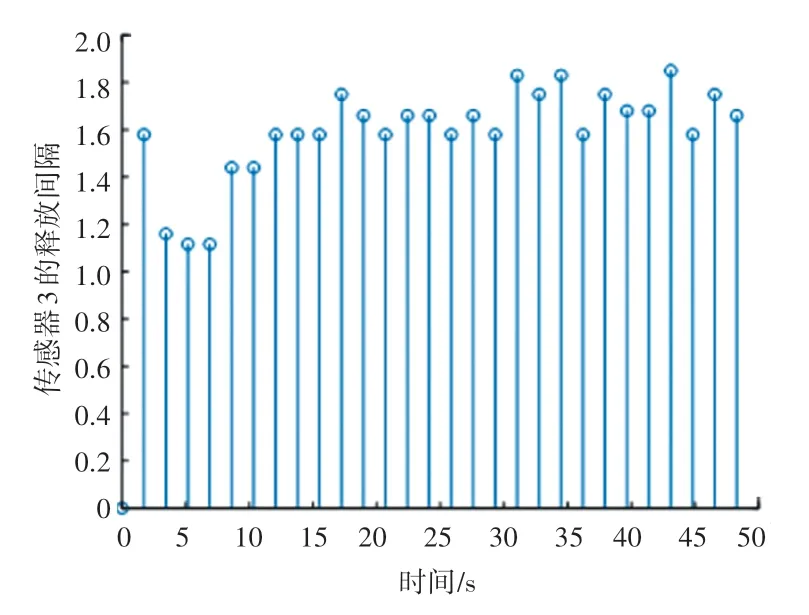
图3 传感器3 的触发和释放Fig.3 Trigger and release of sensor 3
在给定的样本值(1 500)中,传感器1 在事件触发驱动的情况下触发了82 次。
在给定的样本值(1 500)中,传感器2 在事件触发驱动的情况下触发了79 次。
在给定的样本值(1 500)中,传感器3 在事件触发驱动的情况下触发了29 次。
控制系统的状态轨迹如图4 所示,从图中得出该闭环系统渐近收敛到零。在事件触发机制下,传感器1~传感器3 的平均传输率为12.67%,平均传输速率为13.07%[2]。本文增加网络攻击方式,依然能够保证网络的安全,提高带宽的利用率,进而说明本文控制器的优越性。
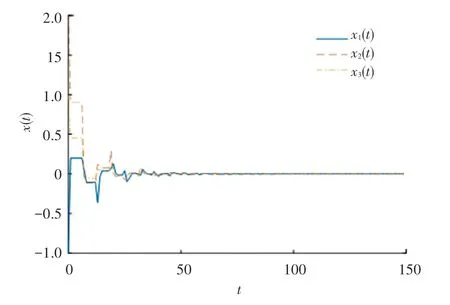
图4 x(t)的状态曲线Fig.4 State curve of x(t)
5 结束语
本文利用时滞神经网络,针对有限的网络带宽结合两种随机网络攻击,研究了H∞神经网络控制器。改进了事件触发机制的触发阀值,进而避免了不必要的数据传输,减轻了网络负担。在构造神经网络控制器时,增加了网络攻击类型,控制器在不同网络攻击下,依然具有良好的鲁棒性。本文构造了新颖的李雅普诺夫函数,对控制器进行了稳定性分析,证明了闭环系统的渐近稳定性,最后通过LMI工具箱,利用数学例子验证了结果的可靠性,并且获得各个传感器触发情况。虽然本文在事件触发,网络攻击等方面进行了改进,同时将多时滞添加到神经网络控制器中,但网络攻击的函数如何取消上下边界的约束,以及自适应事件触发和该模型的结合等问题是仍是今后研究的主要内容。
