计算基坑抗隆起稳定安全系数的卸荷法
2021-12-16阳吉宝
阳吉宝
[上海市政工程设计研究总院(集团)有限公司,上海市200092]
0 引言
基坑抗隆起稳定性验算是基坑围护设计、施工、监测和周边环境保护等各方广泛关注的问题,也是岩土工程界持续进行理论研究和不断探索的课题。目前,基坑抗隆起稳定性分析研究方法有极限平衡法、极限分析法和数值模拟计算法等;但主要用于基坑围护设计工程实践且为我国行业和各省、市规范规程所采用的仍然是地基承载力和圆弧滑动这两种计算模式,其中采用极限平衡理论求得的地基承载力计算模式[1]又分按假定基底光滑情况下的Prandtl(1920)计算式和假定基底粗糙情况下的Terzaghi(1943)计算式;Prandtl计算式较为常用,也被我国行业标准[2]和上海市工程建设标准[3]等大多数省、市规范所采用。Prandtl计算式是一经典的根据极限平衡理论计算地基承载力公式,汪炳鉴、夏明耀[4]最早于1983年提出可以采用此公式进行抗隆起安全系数的验算,以求得基坑围护地下连续墙的入土深度。邹广电[5]分别利用极限分析的上限法和陈立国等[6]利用极限分析法的下限法也都通过推导得出与Prandtl计算式同样的表达式。显然,上述研究始终以墙底下部土体为研究对象,从研究地基承载力为出发点,与基坑开挖卸荷所产生的隆起破坏还是有明显差异。本文在参考郑大同先生一书[7]中对Prandtl计算式推导过程的介绍,依据极限平衡理论,结合基坑开挖卸荷特征,提出基坑抗隆起稳定安全系数验算的卸荷法,并与Prandtl计算式进行敏感度对比分析,尝试从开挖卸荷角度去分析研究基坑抗隆起稳定性。
1 现行规范中的Prandtl计算式
1.1 Prandtl 计算式推导
郑大同[7]曾详细介绍Prandtl计算式的推导过程。
假定材料的容重为零,条形基础宽度为、基础埋深为,Prandtl应用塑性平衡原理,所得的滑动面形成了两个对称的被动状态区及一个主动状态区,中间夹着对数螺线的过渡区,这样就有可能不用高深的数学微分方程来求解,而用力系平衡方法求得条形基础极限承载力计算公式。
为推导极限荷载的计算式,考虑作用在土体OCDI上的力系,见图1(b)。对数螺线CD 的方程为:r=r0eθtanφ,其符号的意义示于图1(a)。由图可看出:
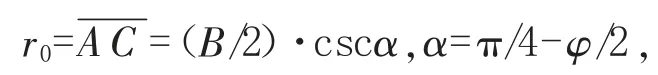
于是r=(B/2)·csc α·eθtanφ。
有:

根据假定,把土体OCDI的重量略去不计。从图1(b)可看出,作用在对数螺线CD 上任意点的法向力与摩擦力的合力F,都通过对数螺线的中心点。这样,就可以把A 点作为矩心,得:

图1 Prandtl 计算式的推导

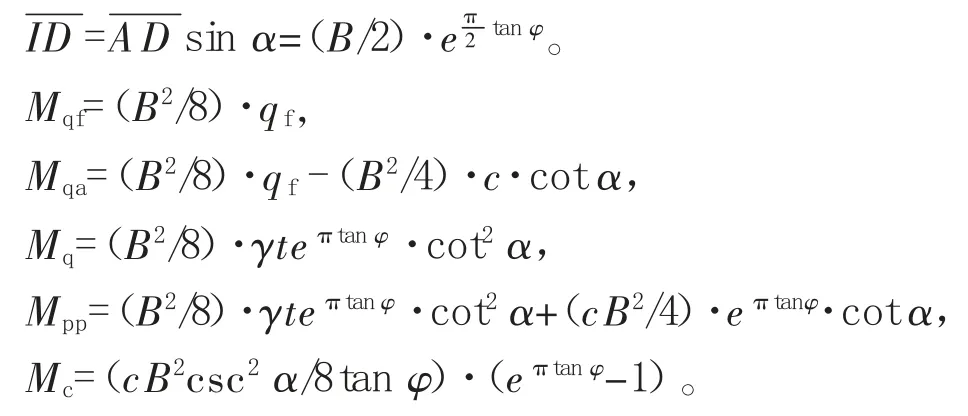
依据平衡条件:
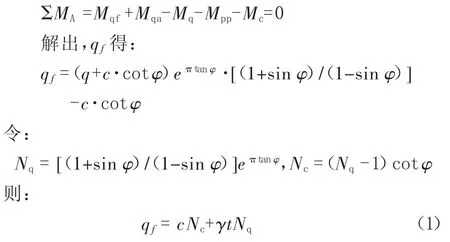
可以看出,Prandtl的极限承载力公式与条形基础的宽度无关;这是由于推导公式时忽略不计地基土的容重,因此Prandtl公式是一个近似公式。
1.2 规范中抗隆起稳定性验算Prandtl 计算式
汪炳鉴、夏明耀[4]最早于1983年提出可以利用式(1)进行抗隆起安全系数的验算,以式(2)的形式来求得基坑围护体地下连续墙的入土深度;后经过研究,式(2)成为验算基坑围护体墙底抗隆起稳定性的承载力计算模式,即Prandtl计算式。我国国家标准、上海市工程建设标准、浙江省工程建设标准《建筑基坑工程技术规程(DB 33/T 1096—2014)》和浙江省宁波市细则《宁波市建筑基坑工程技术细则(2019甬DX-06)》均按式(2)来验算围护墙底抗隆起稳定性,只是Kb取值不同。
当基坑底部土体为淤泥、淤泥质土或粘性土时,坑底土抗隆起稳定性应按式(2)验算围护体墙底地基承载力。

式中:Nq、Nc为地基土的承载力系数,Nq=eπtanφtan2(45°+/2φ),Nc=(Nq-1)tan φ;γ1为坑外地表至围护体墙底或软弱下卧层顶面,各土层天然重度的加权平均值,kN/m3;γ2为坑内开挖面以下至围护体墙底或软弱下卧层顶面,各土层天然重度的加权平均值,kN/m3;h 为基坑开挖深度,m;t 为围护体的插入深度,m;qk为基坑坑外地面超载,kPa;Kb为围护体墙底端土体抗隆起安全系数,不同规范取值不同。
计算图示见图2。
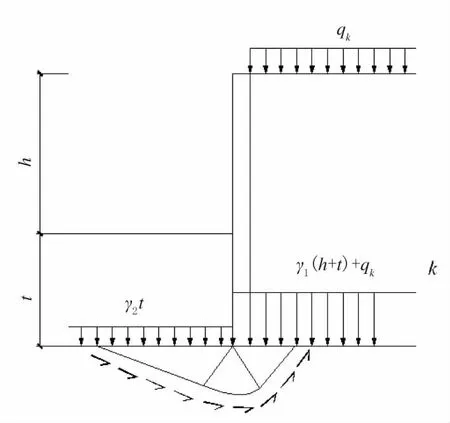
图2 围护体墙底地基承载力验算图示
对于Kb取值,按一级、二级、三级基坑,我国国家标准、浙江省标准和宁波市细则均为分别不应小于1.8、1.6、1.4;上海市标准为分别不小于2.5、2.0、1.7。
2 基坑抗隆起稳定安全系数验算卸荷法
没有开挖就没有基坑隆起破坏。基坑隆起破坏是在竖向开挖卸荷条件下,基坑外侧主动土压力作用下产生的,也即基坑外侧主动土压力是基坑隆起破坏的动力源,是水平向荷载作用。而目前规范方法中的Prandtl计算式,是假定基坑外侧土体作为垂直向荷载作用而引起的地基破坏来计算基坑抗隆起稳定安全系数。为计算卸荷条件下的基坑抗隆起稳定安全系数,参考Prandtl地基承载力抗隆起稳定安全系数的计算式推导原理,依据极限平衡理论,需要对基坑开挖形成的应力场进行概化,首先需根据开挖卸荷特征确定计算的荷载边界条件,然后进行滑动力矩、抗滑力矩计算,最后根据力矩平衡计算抗隆起稳定安全系数。
2.1 确定开挖卸荷计算模型几何边界
基坑开挖在围护体两侧形成主动、被动土压力区,可根据朗肯土压力理论,计算其主动、被动土压力。由摩尔-库仑强度[8]理论可知,当土体达到极限平衡状态时,破坏面与大主应力面的夹角为θ=45°+φ/2。所以,当基坑外侧土体达到主动极限平衡状态时,因水平面为大主应力面,其破坏面与水平面的夹角为θ=45°+φ/2;当基坑内侧土体达到被动极限平衡状态时,因竖直面为大主应力面,其破坏面与水平面的夹角为θ=45°-φ/2。这样就可以确定如图3 所示的计算模型的边界:基坑开挖深度h(m)、围护体插入深度t(m)。

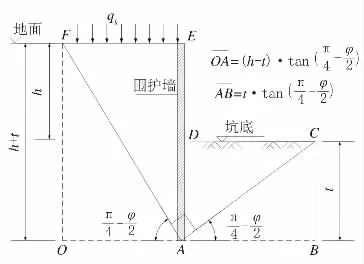
图3 卸荷法计算模型几何边界
2.2 确定计算模型的边界荷载
如图4 所示,在开挖荷载作用下,根据朗肯土压力理论的假定,其主应力方向与水平和垂直方向重合,水平向土压力与垂直向重力呈直角相交,并不产生剪切力。水平向,在基坑外侧OF 侧和基坑内侧BC侧的边界上分别作用有基坑开挖所形成的梯形分布的主动、被动土压力;因基坑开挖导致坑外土体向坑内发生隆起破坏趋势,这样,坑外土体和坑内开挖后剩余土体的重力为抵抗隆起破坏,在围护体端部段和段因坑内、外土体重力作用就产生了抗滑剪力。在竖向,在基坑外侧地面作用有地面超载qk(kPa);在基坑内侧围护体端部作用有因开挖形成的反力γh(kPa)。这样就得到如图4 所示计算模型的荷载边界条件。
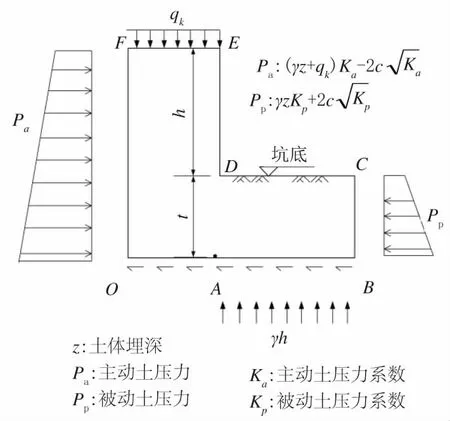
图4 卸荷法计算模型的边界荷载
2.3 计算抗隆起稳定安全系数
根据图4 计算模型及边界条件,以A 点为矩心,根据参考文献[7]中Prandtl计算式的推导原理,运用刚体极限平衡理论,则有:
(1)OF 侧主动土压力产生的滑动力矩

(2)BC 侧被动土压力产生的抗剪力矩


(5)基于开挖卸荷条件下的基坑抗隆起稳定安全系数Kk。

以上所有计算式中的土体参数γ(kN/m3)、c(kPa)、φ(°)分别代表土体重度、粘聚力和内摩擦角。
3 敏感度分析
为科学、合理地分析本文提出的卸荷法中计算式(6)与规范[2-3]中的Prandtl计算式即本文式(2)在反映基坑抗隆起稳定安全系数对各影响因素的敏感性,运用系统分析中的敏感性分析方法[9],评价基坑开挖宽度、挖深、围护体插入深度、土层重度、土体内聚力和内摩擦角等因素对基坑墙底抗隆起稳定性影响的差异。
假定本文提出的抗隆起稳定安全系数为Kk,根据Prandtl计算式[2-3]计算所得的抗隆起稳定安全系数为Kb。通过敏感度比较就可以研究上述两式对各因素的敏感性并进行对比评价。援引参考文献[10]工程实例,并参考已有类似工程经验,影响因素基准参数和变化范围列示于表1。

表1 影响因素基准参数和变化范围
经计算,如图5~图9 所示,两式对各影响因素的敏感度不同,但趋势一致。

图5 与基坑开挖深度的敏感度曲线

图6 与围护体插入深度的敏感度曲线
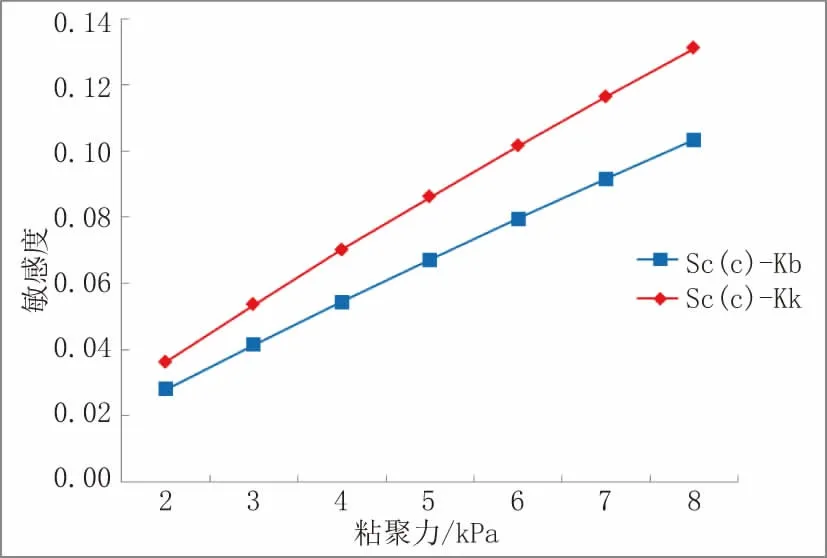
图7 与土层重度的敏感度曲线
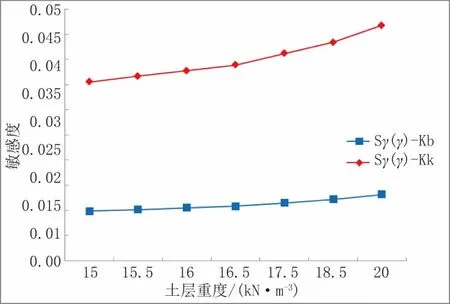
图8 与土层黏聚力的敏感度曲线

图9 与土层摩擦角的敏感度曲线
经对两式敏感度的归一化处理,两计算式对各影响因素的敏感度排序见表2。

表2 影响因素敏感度排序表
从图5~图9 和表2 可以看出,土体的内摩擦角是首要影响因素,这在两个公式均表现一致,但相对于Kb公式,本文提出的计算公式Kk对内摩擦角的敏感程度有较大的降低,由Kb式中的0.5 降至0.349。围护体插入深度和基坑挖深是主要影响因素,公式Kk比Kb对这两因素敏感度要高,说明卸荷法主要反映基坑开挖所形成的主动、被动土压力对基坑抗隆起稳定性的作用,而且对于Kk式,围护体插入深度(敏感度0.330)的影响与内摩擦角(敏感度0.349)的影响接近。土层粘聚力和土层重度是次要影响因素,对基坑抗隆起稳定性影响较小,但卸荷法的土层重度比地基承载力法影响程度要高。
利用表2 中的基准参数计算得到,Kb=1.52,Kk=1.233。Kb>Kk,对于评价基坑抗隆起安全稳定性偏于安全。
4 工程实例分析
本基坑工程位于温州市瓯海区核心片区站南单元A-19 地块,整个用地范围内下设二层地下室,基坑开挖总面积27 610 m2,周长841 m,基坑普遍开挖深度为9.05 m;基坑北侧距基坑开挖边线30 m 有正在运行的轻轨R 1 线,安全等级为一级,其他三侧基坑安全等级为二级。根据勘察报告,项目场地属冲海积平原地貌,地面以下30 m 范围内除浅部3 m 为粘土外,其他均为淤泥。场地分布的②1、②2层淤泥具有分布广泛厚度大、含水量高、孔隙比大、压缩性高、抗剪强度低、灵敏度高等特点。②1、②2层淤泥的基坑设计岩土参数见表3。
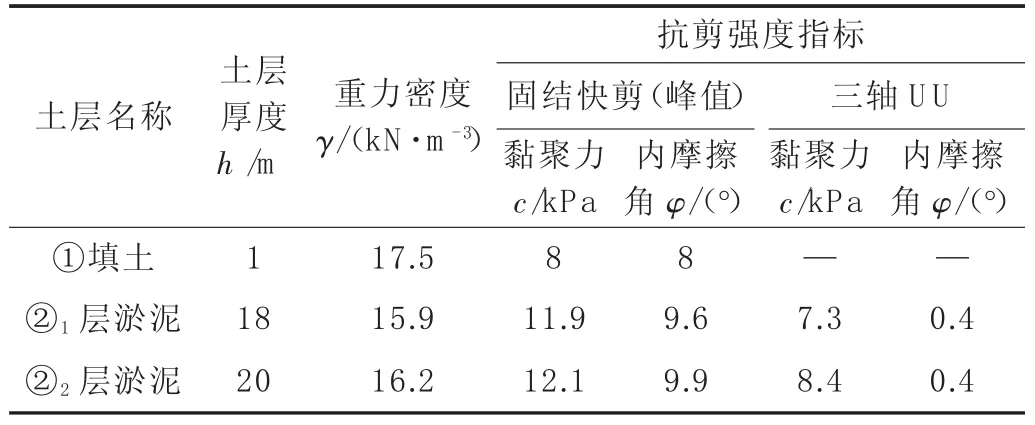
表3 基坑设计岩土参数表
基坑围护设计采用桩径900(北侧)/850(其他三侧)的钻孔灌注桩加二道混凝土内支撑,为优化桩长,按围护桩插入比为1∶1.5~1∶3.0 等7 种情况分别验算基坑墙底抗隆起稳定安全系数Kk和Kb,土层粘聚力和内摩擦角按表3 中固结快剪峰值指标取值,计算Kb时按围护桩桩底所在土层参数取值,计算Kk时,按围护桩桩长范围内土体厚度加权平均值取值,重力密度均按16.1(kN/m3)取值,计算结果见表4。按规范要求基坑围护体四周需满足Kb≥1.6,为保护基坑北侧环境和控制该侧的变形,设计时基坑北侧采用1∶2.2 的插入比,其他三侧采用1∶2.0 的插入比。目前,基坑工程已施工完毕,施工过程围护体变形监测结果也表明基坑北侧最大水平位移控制在25 mm 以内,其他三侧最大水平位移控制在35 mm以内,原设计满足环境保护要求,实践证明原设计的桩长是合理的。利用规范中Prandtl计算式计算所得的Kb始终略大于Kk,但两者均满足规范要求,按Kk式计算偏于安全。

表4 墙底抗隆起安全系数计算结果对比
5 结论与建议
(1)本文根据极限平衡原理,建立基坑在开挖卸荷条件下的围护体墙底抗隆起稳定性验算模式,推导出计算公式,为验算基坑围护体墙底抗隆起稳定性提供了新方法。
(2)通过归一化敏感度分析,本文提出的计算式(Kk)与规范中Prandtl计算式(Kb)对影响基坑抗隆起稳定性的各因素的敏感度排序表现一致。土体的内摩擦角是首要影响因素,相对于Kb,Kk对内摩擦角的敏感程度有较大的降低。围护体插入深度和基坑挖深是主要影响因素,Kk比Kb对这两因素敏感度要高。土层黏聚力和土层重度是次要影响因素,对基坑抗隆起稳定性影响较小,但卸荷法(Kk)的土层重度比地基承载力法(Kb)影响程度要高。
(3)通过温州某已成功实施的基坑工程实例验算分析,本文提出的计算式计算值略小于规范中Prandtl计算式的计算值,与工程实际安全状况相符,也更偏于安全。
(4)本文首次根据基坑开挖卸荷条件,提出基坑抗隆起稳定安全系数计算新方法,或有可能存在不足。建议同行共同对本文提出的计算模式和计算方法开展进一步研究和讨论,并在基坑工程实践中加以验证、完善和推广应用。
