独立互通式立交间的最小净距分析研究

2021-12-16吴晓旭

城市道桥与防洪 2021年11期

曹正，吴晓旭，舒航

（中国市政工程西南设计研究总院有限公司，四川成都 610036）

0 引言

城市外环快速路已经成为现代城市道路的重要组成部分，常与高速公路以相邻独立互通式立交的方式直接连接。而独立互通式立交间的净距常因设置长度不足，引发车流交织混乱，进而导致交通拥堵，甚至会引起交通事故的发生。为有效地消除上述问题的发生，亟需提出一种合理计算独立互通式立交间的最小净距的分析方法。

国内外专家学者在此方面已有一定的研究成果：美国的Bared[1]等人基于行车安全性指标分析，研究了相邻快速路互通立交间的合理间距，给出了安全设计推荐范围；美国TRB 组织[2]在分析独立互通式立交间合理间距时，从道路标志设置、安全性指数、交通量大小，以及线形特征等方面展开，论证了合理净距设置的必然性，结合当地交通量特征进行分析，给出了合理的推荐值。国内针对该问题也有一定的研究基础：高鲁宾[3]等人在参照已有的独立互通式立交净距设置经验，结合实际建设工程项目，针对一定区域内的互通式立交设置密度进行了讨论并给出一定建议，但在具体的独立互通式立交间距分析上没有展开；此外，还有多位专家针对独立互通式立交间距分析研究这一课题展开论证，但大都未建立起具体的量化模型，无法直接指导应用[4-5]。

综上所述可以发现，现行规范和现有研究针对独立互通式立交净距设置未形成一致的结论，尤其是在交通特征、互通结构，以及互通类型存在差别时，其最小净距设置存在经验性主导的弊端，无法有效贴近车辆分布特征及驾驶人员感受，从而引发各类交通问题。基于此，搭建了最小净距数学分析模型，在剖析车辆驾驶人员获取、分析道路信息、作出决断，以及操纵车辆响应全过程的基础上，搭建变换车道场景模型；结合工程经验，确定变换车道转角与行车速度间的递归关系；分析车辆获取可接受间隙过程中的行进距离，获得独立互通式立交间的合理最小净距；并结合公路立交设计实例展开论证。其研究成果能为独立互通式立交间的合理净距设置提供一定的参考价值。

1 交通特征及净距概念分析

1.1 交通特征分析

城市外环快速路作为现代城市交通的主干道组成部分，同时兼备公路特征，能够便捷快速地连接城际、城内及区间交通。

设置于城市外环快速路中的各类互通式立交是快速路实现快速便捷连通的重要关口。其设置密度不宜过大，否则将无法实现通行车辆的安全快速运转，尤其是频繁的车辆车道变换操作，容易阻碍快速路快速通行特征的发挥，甚至会引发各类交通问题。此外，不同城市快速路的交通等级、交通量，以及交通流特征也存在一定区别，互通式立交结构形式也存在着较大差别，因此，现着眼于搭建独立互通式立交间最小净距数学分析模型，以获得合理的工程指导数据。

1.2 净距概念分析

独立互通式立交间的净距指的是同行驶方向上，后方互通式立交加速车道终止处，到前方互通式立交减速车道起始处的须保留的距离范围。考虑到各互通式立交车道布置形式的差别，可分为如下三种类别，如图1～图3 所示。

图1 独立互通式立交连接方式1 图示

图2 独立互通式立交连接方式2 图示

图3 独立互通式立交连接方式3 图示

其中，图1 和图2 所示的两种独立互通式立交连接方式适用于两者之间净距较短、容易导致行车流交织混乱的场景，采取了设置辅助车道的形式，连接后方互通式立交加速车道和前方互通式立交减速车道，以避免过多的车流交织影响正常直行车辆。图3 所示的两种独立互通式立交连接方式适用于两者之间净距较长的场景，该种方式不会对正常直行车辆产生明显影响，可作为一个独立区域，能够有效地控制施工造价和占地面积，也是本文所研究数学分析模型的主要参照。

2 最小净距数学分析模型

2.1 模型选择分析

按照驾驶人员的行车实际状况，独立互通式立交间的合理净距设置需要贴合驾驶人员在行车流交织过程中获取、分析道路信息、作出决断，以及操纵车辆响应的全过程，选取了最不利分析方案，如图4所示。

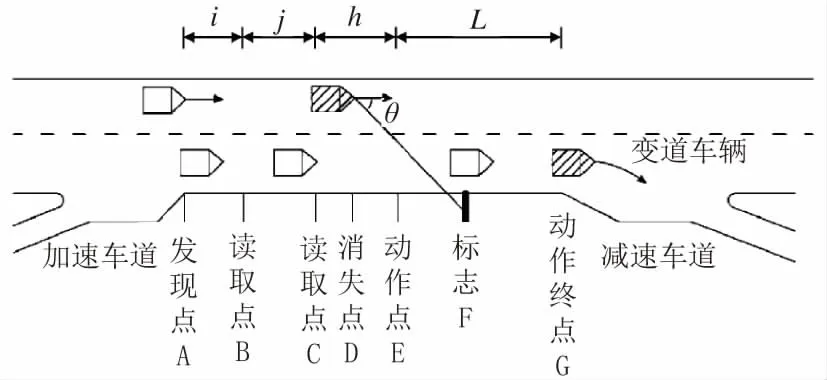
图4 道路信息识认过程图示

将上述过程划分为两个主要组成部分：第一部分为道路信息获取-分析-决断阶段，也就是驾驶人员在后方互通式立交加速车道终止处A 发现交通标志牌，在B-C 期间读取标志牌，在C-E 期间分析道路信息、作出决断；第二部分是操纵车辆响应阶段，也就是在完成道路信息获取、分析、决断后，处于内侧车道的车辆变道至外侧车道并从前方互通式立交减速车道驶出的过程E-G。上述全过程中驾驶人员所需的总净距LJ为：

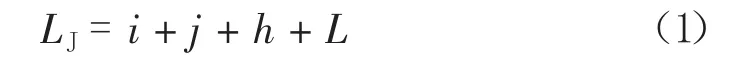
2.2 计算参数选取

2.2.1 道路信息获取-分析-决断阶段

在车辆行进的过程中，驾驶人员处于高速运动状态，其视觉信息获取能力与静止状态存在一定的差别，且随着其运动速度的加快，驾驶人员的注意力集中点视距范围、视角均将随之产生变化，如图5 所示。因此，独立互通式立交间应降低非必要交通标志设置密度。

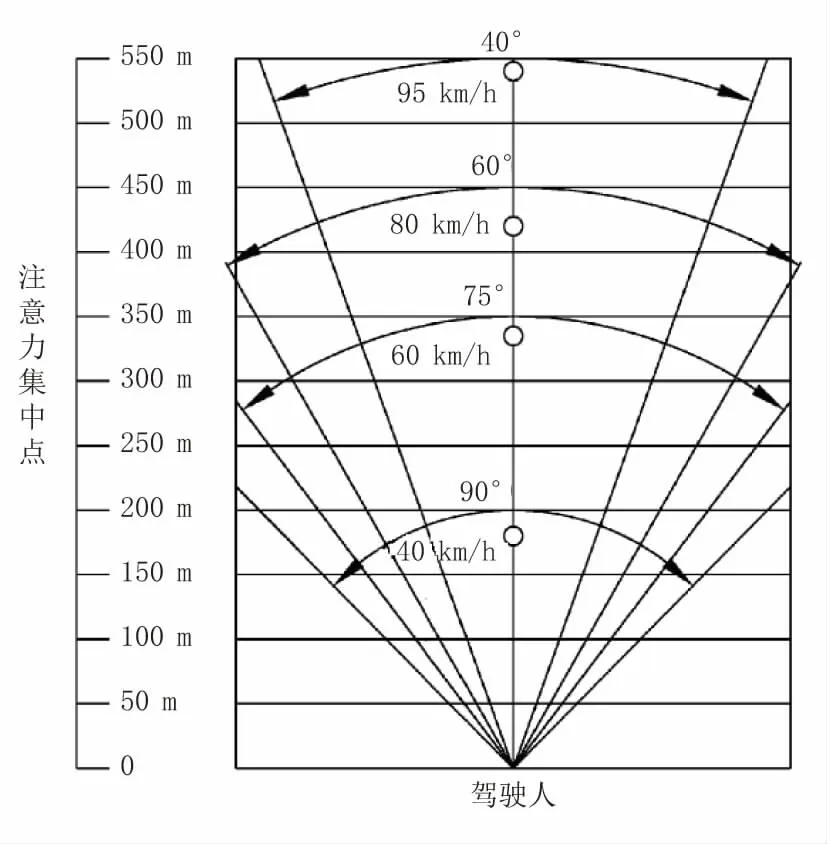
图5 驾驶人员视距范围、视角变化示意图

一般可以认为人体视觉系统获取一个目标物的时间为0.5 s，读取清晰所需的时间为1.0 s，因此可取i为0.5v，j 可取1.25v，其中v 为车辆行驶速度。在驾驶人员识别出标志牌信息后要对道路信息进行分析、作出决断，这一时间平均为2.0 s，即h 可取2.0v。

2.2.2 操纵车辆响应阶段

内侧车道行驶的驾驶人员在实施变道操作时，须在其外侧车道获取可插入间隙，并以一定的角度θ实施变道，可概括为两个部分，其中第一部分为车辆获取可接受间隙过程中的行进距离，第二部分为实施变换车道过程的行进距离。

2.2.2.1 变道过程分析

车辆在实施变换车道的过程中，其x 和y 方向的运动方程如下：

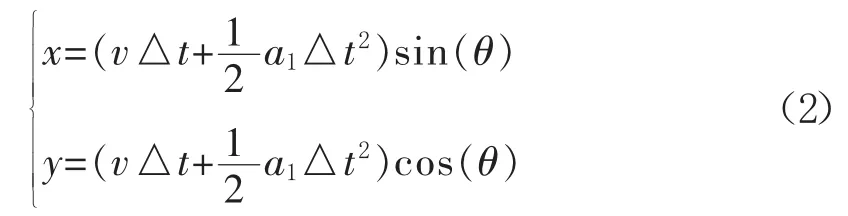
式中：a1为内侧车辆变换车道时的加速度，可取1.5 m/s2；△t 为变换车道所需时间，s。

已有研究表明[6]：角度θ 通常小于1.6°，且行车速度越大，角度θ 越小，两者存在如下关系式：

因此，在明确v 的基础上可计算得到相关角度θ值，在明确横向距离x 的基础上进而通过公式（2）计算出△t，最终可计算得出纵向距离y。

2.2.2.2 可接受间隙分析

相对内侧车辆变换车道至外侧时，外侧车道的车间距τ 应满足：

式中：△S 为安全距离，如图6 所示，其值与速度的关系见表1 所列。

图6 变道过程示意图

表1 安全距离与车速对照表

根据距离相对逻辑关系，以及行车速度距离管理，可以确定外侧车道产生驾驶人员可接受间隙时外侧车道的车辆排队长度S1和等待期间内外车道产生的行驶距离差S2关系如下：

其中，n 指的是驾驶人员可变道空档数量，可通过交通流理论进行取值；V1指的是内侧车道车辆行驶速度；V2指的是外侧车道车辆行驶速度；Vmin指的是内侧车道最低速度，a2指的是变道车辆加速度，一般可取-2 m/s2（车辆减速）。

进而确定外侧车道产生驾驶人员可接受间隙的等待时间t，以及车辆在内侧车道行驶的距离S 关系如下：

根据公式（2）和公式（6），可以计算得到L=（N-1）（S+y），进而可以推得：

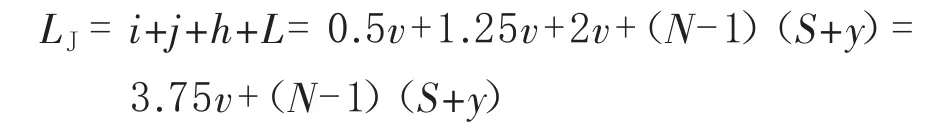
3 工程实例计算

3.1 参数情况

现依托四川省某城市外环高速快速干线工程进行计算论证。该干线为双向六车道，设计时速分为80 km/h 和100 km/h 两段。其中，80 km/h 限速段的内、中、外车道限速范围分别为：60～80 km/h、50～80 km/h 及50～60 km/h；100 km/h 限速段的内、中、外车道限速范围分别为：80～100 km/h、70～100 km/h及60～80 km/h。