应用统计学专业实践教学案例的量化分析
2021-12-16胡攀
胡 攀
(四川文理学院 数学学院, 四川 达州 635000)
0 引 言
《国家中长期教育改革和发展规划纲要(2010-2020 年)》中提出了在人才培养体系改革中要“注重知行统一”,“坚持教育教学与生产劳动、社会实践相结合”,突出强调了高校在人才培养工作中加强大学生实践教学培养的重要性.[1]应用统计学专业具有较强的实践性、应用型和综合性特点,而实践教学是本专业人才培养方案的重要组成部分.实践教学不仅可以培养学生的创新精神和实践能力,而且能培养学生理论联系实践,提高实际动手能力和分析问题、解决问题的能力.
为了全面深入贯彻落实党的十九大精神和习近平新时代反腐倡廉建设的新思想、新部署和新要求.四川文理学院数学学院受川东A市纪委委托,对本市辖区范围内58个申请创建“廉洁细胞”的单位,按照六大类“廉洁细胞”的建设标准,通过问卷调查的方式进行第三方监测评估,以巩固和发展A市良好的政治生态.数学学院接到任务后,深知本次监测评估工作即是一项艰巨的政治任务,更是应用统计学专业一次难得的实践教学机会.通过本次实践活动,既可以加强应用统计学专业实践教学内容与考核方式的建设,又可以培养学生的创新精神和实践能力,还可以检验本专业的教学质量.
传统的应用统计学专业的实践教学研究,主要是从定性的角度进行分析和总结.[2-5]从定量的角度进行分析和研究的成果少之又少.因此,本文以川东A市六类“廉洁细胞”工程建设中“廉洁机关”的建设为例,通过问卷调查的方式,综合运用数学建模和描述性统计的思想和方法,对10个申报建设“廉洁机关”单位的调查问卷进行量化分析,探索应用统计学专业实践教学的过程和内容设置,希望能加快完善本专业的实践教学体系.
1 调查问卷设计概述
做好应用统计学专业的实践教学,既是提高本专业人才培养质量的重要保证,也是培养学生理论联系实践的主要途径.作为应用型与实践性较强的专业,要搞好实践教学,关键是做好两方面的工作:一方面是做好抽样与调查;另一方面是运用恰当的方法对抽样调查的结果进行整理和分析.抽样与调查作为实践教学的主要内容,既是前期获取高质量调查数据的保证,又是后期对调查结果整理和分析的基础.因此,做好抽样与调查环节,能使实践教学达到事半功倍的效果.本节结合川东A市“廉洁细胞”工程建设中“廉洁机关”的建设,介绍调查问卷内容的设置与抽样方法的选取.
1.1 调查问卷内容的设定
根据川东A市纪委《关于对“廉洁细胞”创建示范单位进行考评验收的通知》要求,本次监测评估需对“廉洁细胞”建设情况和整治“群众最不满意的10件事”活动成效进行监测评估.基于此,本次评估将调查问卷的内容设置为:机关制度设定、机关作风、宣传教育、社会评价和整治活动成效五个方面.
1.2 抽样方法的确定
为了全面了解川东A市“廉洁机关”建设的成效,依据调查问卷的内容,按照分层抽样的方法,将各申报点的调查对象分为中层及以上机关领导、机关普通员工和机关服务的群众三个层.考虑到机关单位中,中层及以上领导人数较少,采用随机抽样可能会造成较大误差,所以,对机关领导采用整群抽样的方式进行问卷调查.根据黄金分割比,对机关普通员工按照62%的比例进行随机抽样.由于部分机关的服务群众具有人数多、分布广、调查难度大的特点.因此,监测评估小组到各机关单位的办事窗口随机抽取100名群众进行问卷调查.[6]各机关单位的调查内容、题目数量和抽样方法见表1.各机关单位抽样总体分布及问卷整理结果见表2.

表1 各机关单位调查内容分配明细
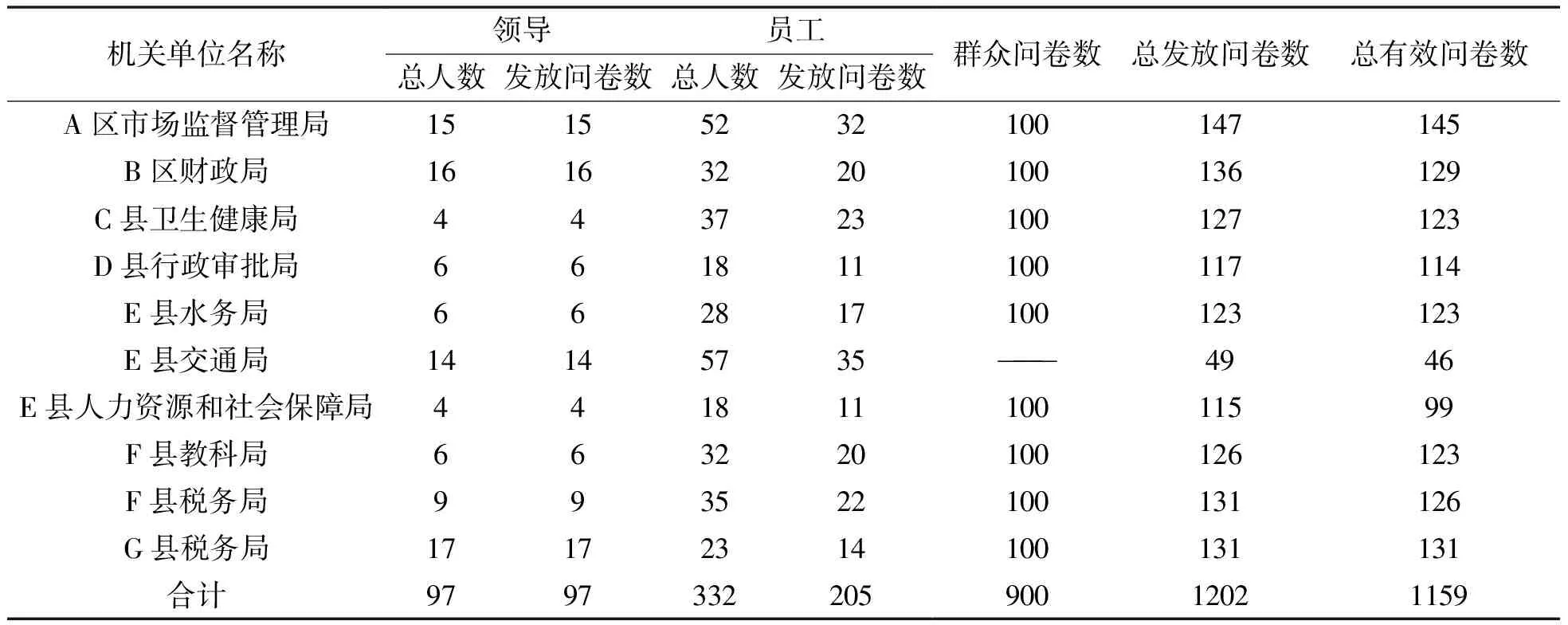
表2 各机关单位抽样总体分布及问卷整理结果
将调查问卷的结果录入excel表格中,将未填写完整的问卷、填写过程中存在逻辑错误的问卷及部分答案选择不明确的问卷均视为无效问卷,整理过程中共删除无效问卷43份.表2中总有效问卷数=总发放问卷数-无效问卷数.
2 监测评估成绩统计的数学模型
问卷调查结果的整理和分析是应用统计学专业实践教学的另一项主要内容,运用恰当的数学统计方法分析调查结果,从分析中发现问题、提出问题进而解决问题,这既可以培养学生将所学基本知识和基础理论用于解决实际问题的能力,又可以进一步探索专业实践教学的内容和考核方式.为了对“廉洁机关”的问卷调查结果进行量化分析,并最终以百分制的形式对10个机关单位的廉政建设成效进行排名.本节借助数学建模的思想和方法,建立问卷成绩计算的数学模型.[7]
2.1 权重系数的确定
首先将 “廉洁机关”调查问卷中的问题分为正向问题和反向问题两类;其次,依据每小题的答案选项设置答案权重,并将每小题的答案权重分为普通权重和特殊权重两类.规定:① 每小题中积极性和正向性强度越强的答案,权重系数越高,反之亦然.② 对于问卷中选项后面留有填空的题目,领导和普通员工如果选了对应选项,但选项后面填空内容留空白,视本小题权重为0,如果选了对应选项,依据选项后面的填空内容设置特殊权重(如:领导问卷中的第8小题,员工问卷中的8、9小题);③ 对于题目后面没有选项只有填空的小题,将根据问卷答案设置特殊权重(如:群众问卷的第7小题).最后,结合每小题的答案选项数量和强度等级(强度等级由强到弱依次定为I级、Ⅱ级、Ⅲ级和Ⅳ级),制定各答案的权重系数. 特殊权重系数范围[0,1],普通权重系数见表3.

表3 不同答案选项的普通权重系数
2.2 监测评估成绩统计的数学模型
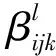
(1)
由于三类调查问卷的题目数量各不相同,各小题的赋分结果也不尽相同,造成三类调查问卷的总分均不是百分制,不便于后续统计分析和排序.因此,需要先对三类调查问卷的实际得分作如下百分制转化:
(2)
记nij表示第i个监测点第j类问卷的问卷份数,从而可得第i个监测点第j类问卷的平均得分为:
(3)
记α1,α2,α3分别表示领导、员工和群众问卷得分在总评成绩中的比重.综上可得监测评估成绩的数学模型:
(4)
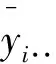
3 监测评估成绩统计与分析
3.1 监测评估成绩统计
结合上节的数学模型,编程求出川东A市“廉洁机关”建设10个监测评估点的考评成绩及排名如表4.
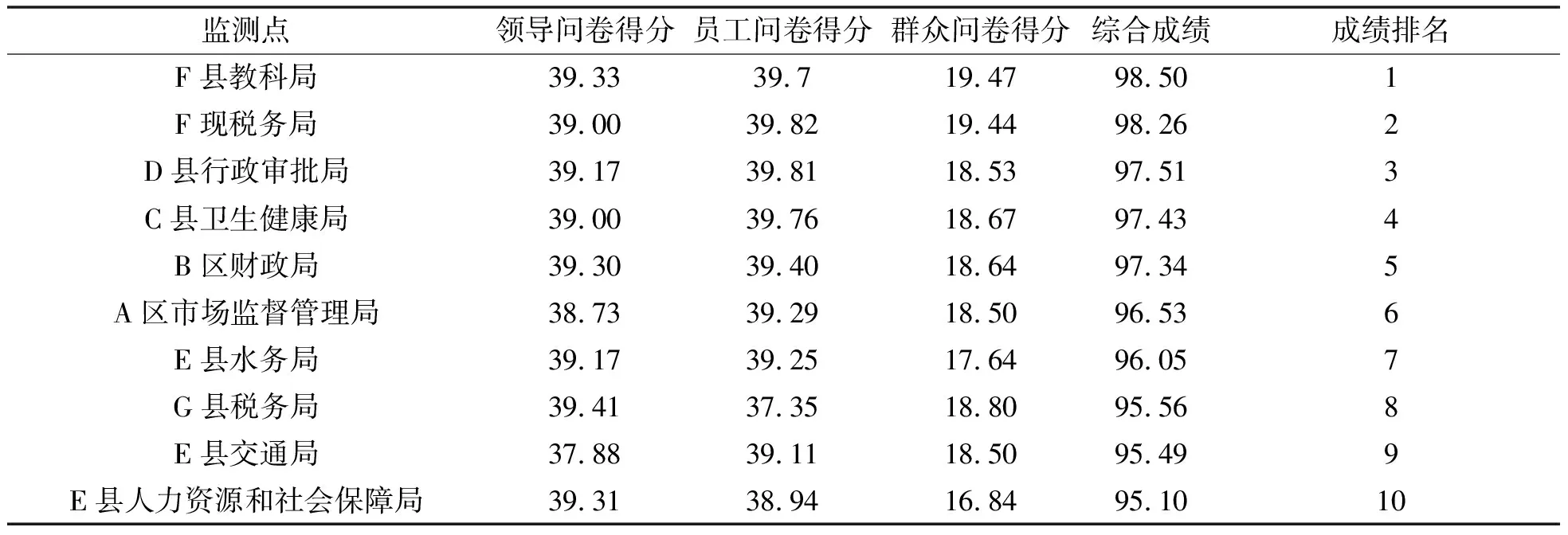
表4 监测评估点考评成绩及排名
由于E县交通局的原因,造成本单位的群众问卷缺失,在成绩处理过程中,将其余9个单位群众问卷的综合成绩取平均后作为E县交通局的群众问卷得分.表中的问卷得分是在问卷得分百分制转化基础上乘以总评得分权重系数后的结果,权重系数α1,α2,α3分别取0.4,0.4和0.2.
3.2 考评成绩统计分析
(1) 描述性统计分析
从表4的数据统计结果可知,10个监测评估点领导问卷平均得分39.03,最高得分39.41,最低得分37.88,极差为1.53;机关单位员工问卷平均得分39.243,最高得分39.82,最低得分37.35,极差为2.47;群众问卷平均得分18.503,最高得分19.47,最低得分16.84,极差为2.63.
(2) 综合成绩结构对比分析
10个“廉洁机关”监测评估点的综合成绩差异不大,为了看清各监测评估点综合成绩差异的本质,将10个监测评估点领导问卷成绩、员工问卷成绩和群众问卷成绩绘制成如下蜘蛛图.[8]

图1 各监测评估点问卷成绩结构对比图
从图1可知,E县人力资源和社会保障局和E县水务局群众得分偏低,是导致两单位综合成绩排名靠后的直接原因;G县税务局员工得分略低于其它区县,也是导致该县综合成绩偏低的主要原因;E县交通局机关领导得分略低,导致其成绩排名靠后.
(3)相关性检验
下面讨论10个“廉洁机关”监测评估点领导问卷、员工问卷和群众问卷得分之间的相关关系.由于只有10个评估点,数据不具有正态性,不宜使用Pearson相关性检验,此处考虑Spearman秩相关系数检验和Kendallτ相关系数检验.[9]
Spearman秩相关系数检验的假设为:
H0:ρ=0↔H1:ρ≠0
(5)
Spearman秩相关系数:
(6)
其中,Ri表示Xi在(X1,X2,…,Xn)中的秩,Qi表示Yi在(Y1,Y2,…,Yn)中的秩.其对应的检验统计量:
(7)
当T>tα(n-2)或P(T>tα(n-2))<α时,拒绝原假设,表明两变量有相关关系,反之则不能表明有相关关系.
Kendall于1938年提出另一种与Spearman秩相关系数检验相似的检验方法.设有n对观察值(X1,Y1),…,(Xn,Yn),若乘积(Xj-Xi)(Yj-Yi)>0,∀j>i,称数对(Xi,Yi)与(Xj,Yj)满足协同性;若乘积(Xj-Xi)(Yj-Yi)<0,∀j>i,则称该数对不满足协同. Kendallτ相关系数统计量:
(8)
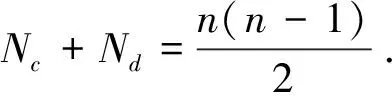
在95%的置信水平下,用上述两种非参数相关性检验方法进行检验,结果见表5.
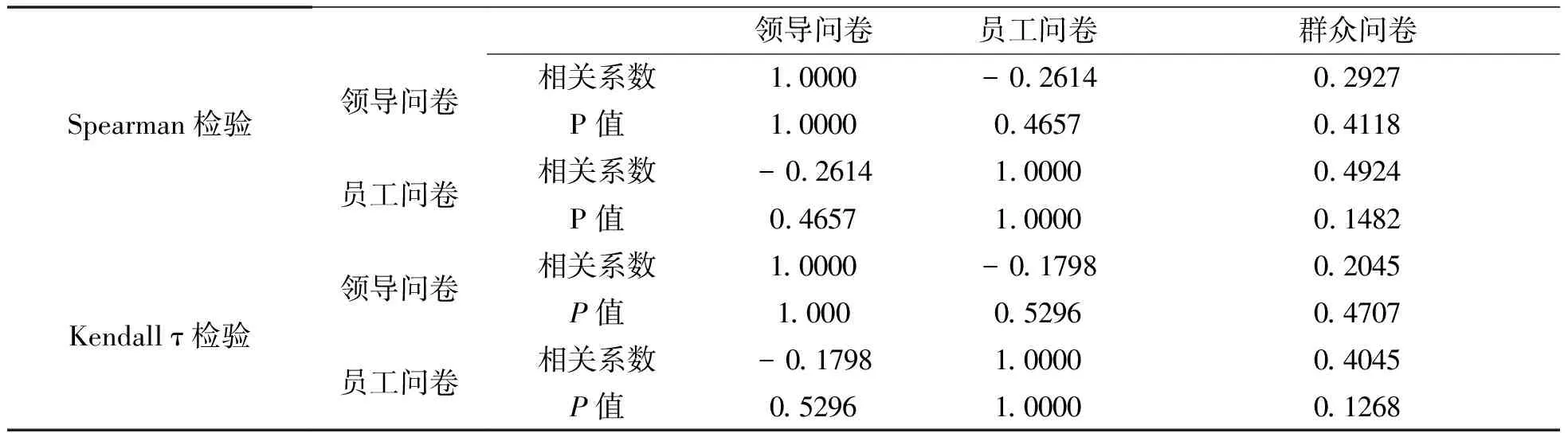
表5 两种非参数相关性检验结果
表5中的数据结果表明,尽管领导问卷、员工问卷和普通群众问卷的相关系数均不为0,但在95%的置信水平下,所有的概率值均大于0.05,故接受原假设,即认为三类调查问卷成绩两两间不存在相关性.用上述两种非参数相关性检验方法进行检验的数值结果有一定差别,主要是由两种检验方法的统计量不同造成的,并不影响最终的结果判定.
结 论
针对现实生活中的具体实例,将数学建模和描述性统计的思想和方法有机结合起来,从定量的角度,介绍应用统计学专业实践教学的内容和方法,具有一定的理论研究意义和实际应用价值.用自然科学的方法解决社会科学类问题,从方法论的角度看,是一次大胆的尝试,它将定性的问题转化为定量研究,且数值研究的结果表明,此方法具有一定的可行性.前期问卷问题设置的不足,使得后期在选用统计方法对调查结果的分析上显得过于单一,很难进行深层次的数据挖掘与分析,但这并不影响本次监测评估结果的可信度.
