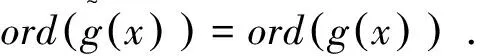斜互反多项式的阶
2021-12-16朱帅樱范逸鹏
朱帅樱,范逸鹏,谢 涛
(湖北师范大学 数学与统计学院,湖北 黄石 435002)
1 引言与预备引理
在本文我们用Fq表示阶为q的有限域,用Fq[x]表示在Fq上的多项式所构成的集合,并用def(f(x))表示这个多项式的次数.在文献[1]中Rudolf Lidl、Harald Niederreiter和P.M. Cohn给出了多项式的阶的定义,即:f(x)∈Fq[x]为非零多项式,若f(0)≠0,则满足f(x)|xe-1的最小正整数e,称为f(x)的阶,记为ord(f(x));若f(0)=0,则有f(x)=xhg(x),其中h∈,g(x)∈Fq[x],g(0)≠0,则记ord(f(x))=ord(g(x)).并且文献[1]中作者还提出了互反斜多项式的定义,即:
定义1:[1]设
f(x)=anxn+an-1xn-1+…+a1x+a0∈Fq[x],其中an≠0.
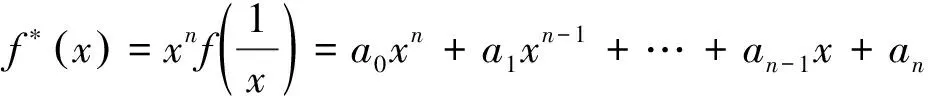
由此本文在f*(x)定义的基础上提出了f(x)的斜互反多项式的定义,即:

在文献[1]中作者得出了ord(f(x))与ord(f*(x))之间的关系,即:
引理1[1]:设f(x)Fq[x]为上的一个非零多项式,且f*(x)为f(x)的互反多项式,则有ord(f(x))=ord(f*(x)).
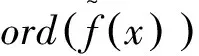
下面给出本文需要的有关引理.
引理2[1]:设c为正整数,且多项式f(x)∈Fq[x],f(0)≠0,则f(x)|xc-1当且仅当ord(f(x))|c.
引理3[1]:设非零多项式g1(x),g2(x),…,gk(x)∈Fq[x],且(gi,gj)=1,1≤i,j≤k.令f(x)=g1(x)g2(x)…gk(x),则有ord(f(x))=[ord(g1(x)),…,ord(gk(x))].
2 斜互反多项式的阶
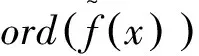
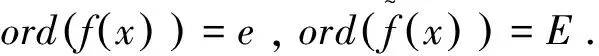
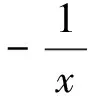
两边同时乘以xn可得
整理得
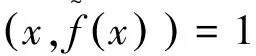
可得
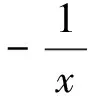
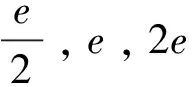
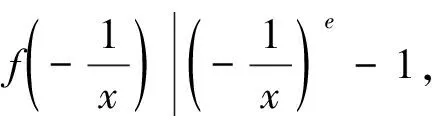
故有
整理得
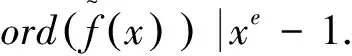
当e=h,其中h为奇数时,则由f(x)|xe-1可知
故有
由e为奇数可知
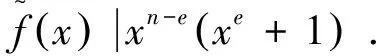
当e=2h,其中h为奇数时.先设f(x)=gb(x),其中g(x)为不可约多项式.由f(x)|x2h-1
可知f(x)|(xh-1)(xh+1).
又f(x)不整除xh-1(若f(x)|xh-1则有ordf(x)|h,但由于ord(f(x))=2h,矛盾),因此有
f(x)|xh+1.
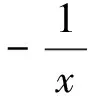
两边同时乘以(-1)nxn可得
整理得
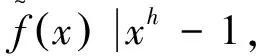
ord(f(x))=[ord(g1(x)),…,ord(gk(x))].

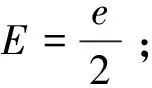
再考虑f(0)=0的情况,此时f(x)=xhg(x),g(0)≠0.由定义1可知
ord(f(x))=ord(g(x)).