轮毂低压铸造缺陷预测数学模型研究
2021-12-16何静瑜
何静瑜
(江苏信息职业技术学院 基础课部,江苏 无锡 214153)
0 引 言
低压铸造是一种由下而上利用压力将液态金属合金压入铸型型腔,同时在压力作用下凝固成型的一特种铸造方法,主要用于汽车轮毂、内燃发动机的气缸体、导弹外壳等形状复杂镁合金件的零件铸造成型,其在汽车、国防等领域得到广泛应用并具有重要的基础地位,[1-2]然而低压铸造成型铸件易产生"缩孔、疏松"等铸造缺陷,将导致铸件成品率低.低压铸造工艺参数的选择,对成品质量有着重要的影响,为了优化工艺参数,减少因工艺参数的选择不当而导致铸件成品率低,学者们研究了低压铸造的工艺优化问题.张响等人根据模拟结果,采用BP人工神经网络建立了工艺参数与缩松缺陷、凝固时间、温度等之间的数学模型,并利用GA算法实现了对低压铸造工艺的优化.[3]张雅晴等人基于正交试验方案讨论了浇注温度、模具预热温度、充型速度等参数对C5M4端盖低压铸造影响并实现其参数的优化.[4]王朝涛等人基于神经网络和遗传算法建立了浇注温度、模具预热温度、传热系数和模具壁厚等影响铸造因素与温度场模拟、有效应力之间的关系并通过GA算法实现了参数优化,并提高了成品的质量.[5]李宁等人利用响应面方法建立了模具结构、压铸工艺参数与低热应力等之间的数学关系,并实现了参数的优化,提高铸件品质.[6]为提高汽车轮毂低压铸造成品质量,优化铸造工艺参数,本文提出了一种基于代理模型技术汽车轮毂低压铸造工艺参数与缩松缺陷体积之间的关系建模方法;代理模型主要有kriging、[7]响应面、[8]神经网络、[9]支持向量机等,[10]本文提出了一种基于QPSO-SVR算法的轮毂低压铸造缩松缺陷体积预测数学模型,利用SVR算法建立低压铸造工艺(模具预热温度、浇注温度、浇注速度)与缩松缺陷体积之间的数学模型,同时采用QPSO算法对SVR 算法进行优化,提高数学模型的精度,并利用有限元方法验证数学模型的正确性,建立的数学模型能有效的实现轮毂低压铸造缩松缺陷体积预测,也为采用相应的智能优化算法对其优化奠定了基础,能够实现压铸成型工艺参数与热应力之间的最佳匹配
1 轮毂低压铸造试验设计与数值模拟
1.1 试验设计
本文主要讨论低压铸造工艺与缩松缺陷体积之间的数学模型,工艺参数选择模具预热温度、浇注温度、浇注速度三个工艺参数,每个工艺参数取5个水平,具体的工艺参数水平取值如表1 所示.
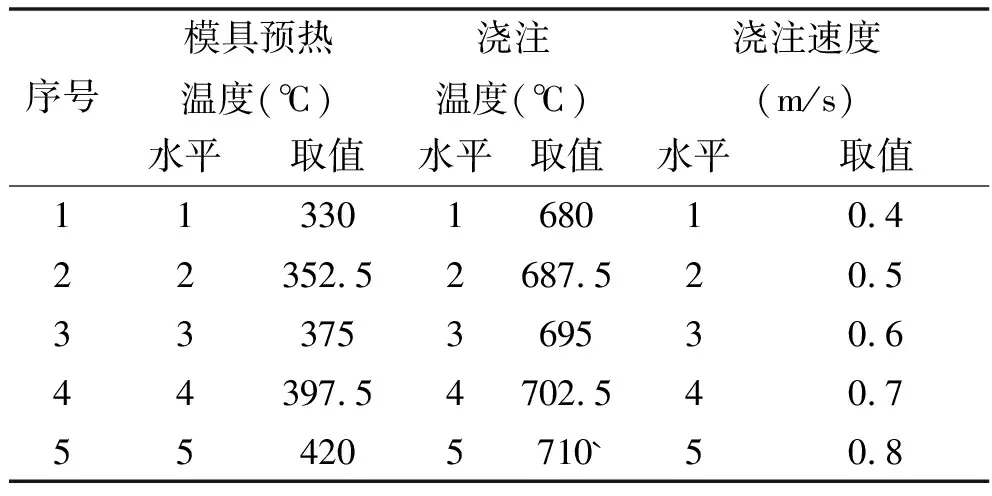
表1 工艺参数及其水平取值
采用正交试验方案完成试验设计,正交试验结果如表2 所示.

表2 正交试验结果
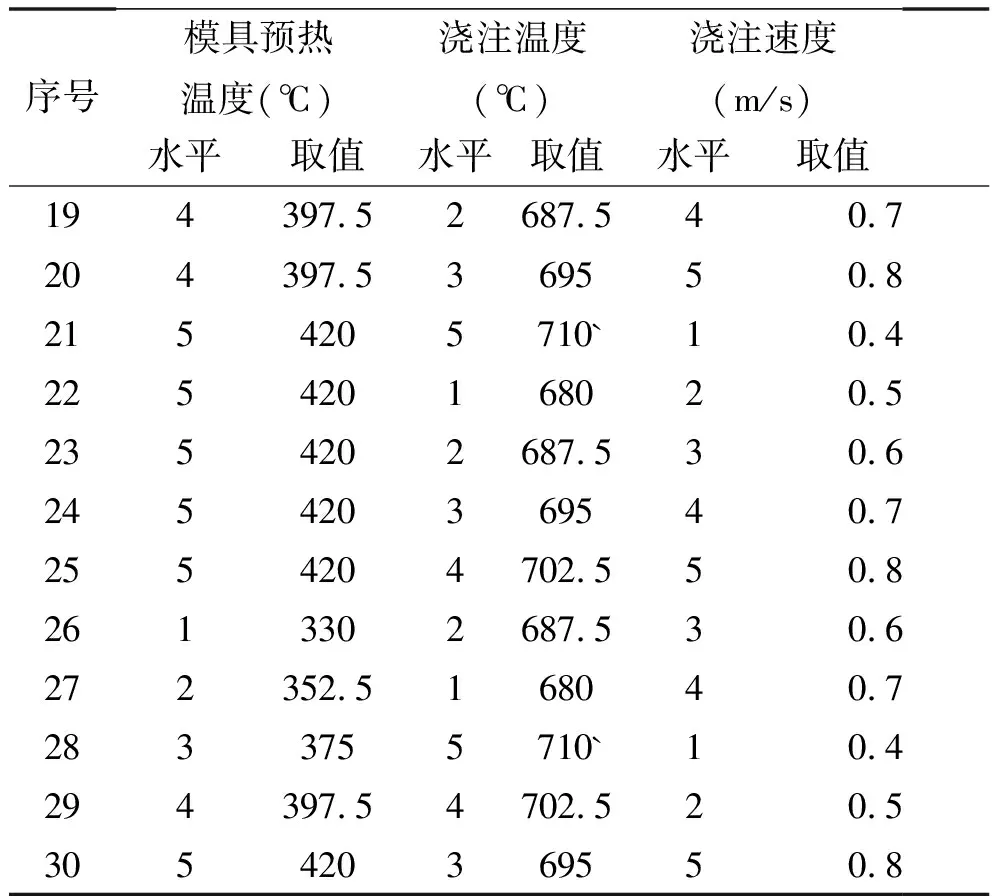
序号模具预热温度(℃)浇注温度(℃)浇注速度(m/s)水平取值水平取值水平取值194397.52687.540.7204397.5369550.82154205710`10.4225420168020.52354202687.530.6245420369540.72554204702.550.82613302687.530.6272352.5168040.72833755710`10.4294397.54702.520.5305420369550.8
1.2 轮毂低压铸造数值模拟
利用PORCAST铸造仿真软件进行轮毂低压铸造数值模拟仿真,浇注方式为“底注式”,分别得到正交试验各组参数组合下的轮毂铸造缩松体积情况.以参数正交试验的第一参数工艺参数为例,说明具体的仿真过程和结果,图1为轮毂的三维模型,图2 则为有限元模型,图3则为不同分析步下轮毂铸造的充型过程与凝固过程,图4为轮毂铸造缩松分布情况.

图1 轮毂三维模型

图2 轮毂有限元模型
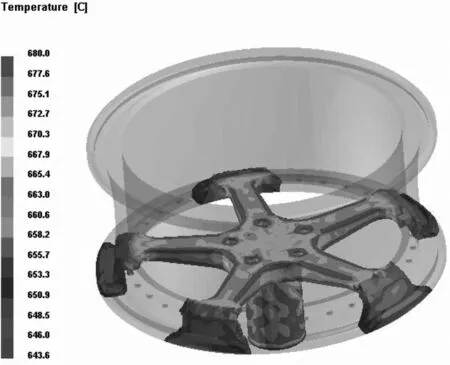
(a)第100步
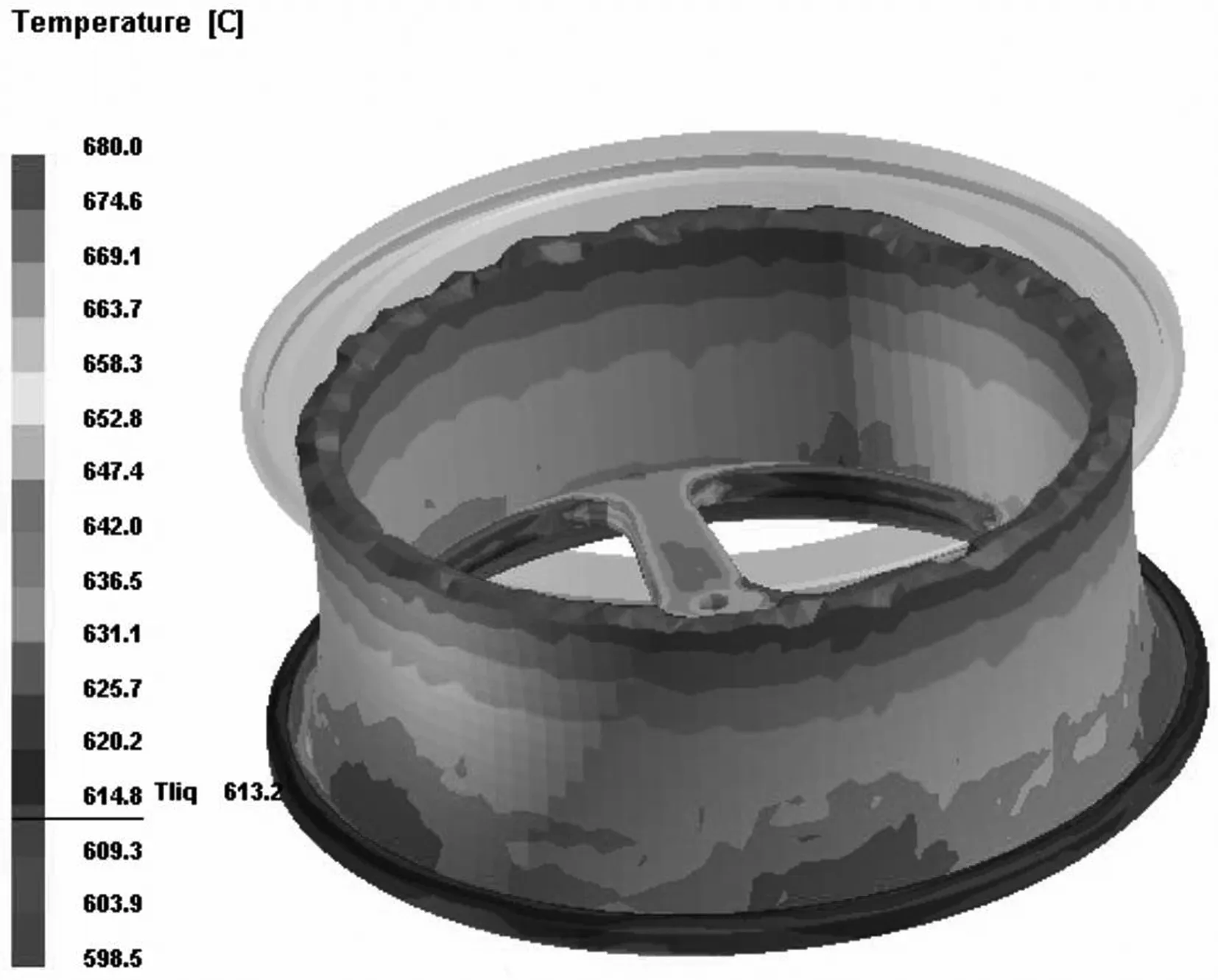
(b)第300步

(c)第500步
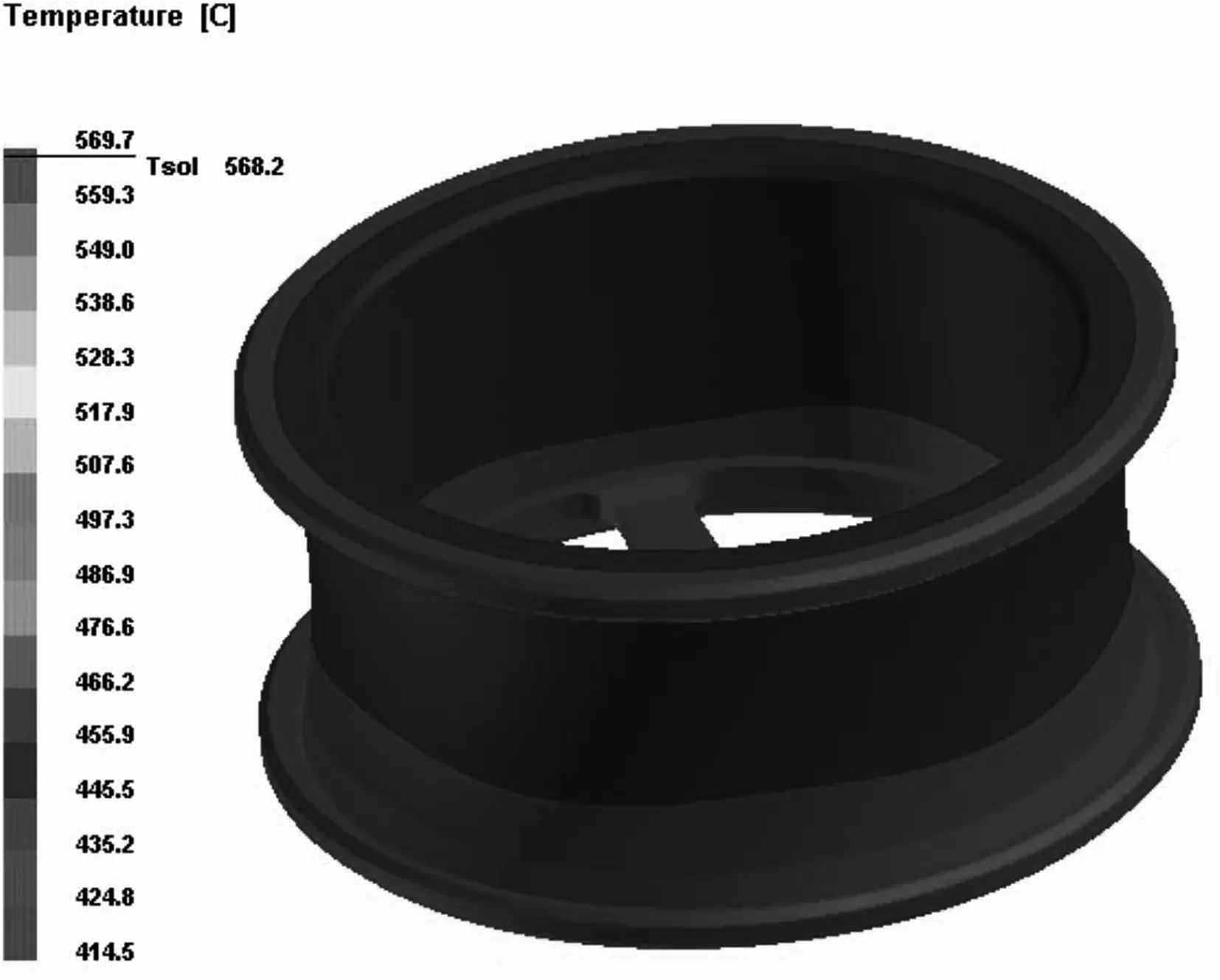
(d)第700步

图4 轮毂铸造缩松
采用上述分析过程,对每一组正交试验进行模拟仿真,分析不同条件下的轮毂铸造缩松情况,具体结果如表3所示.
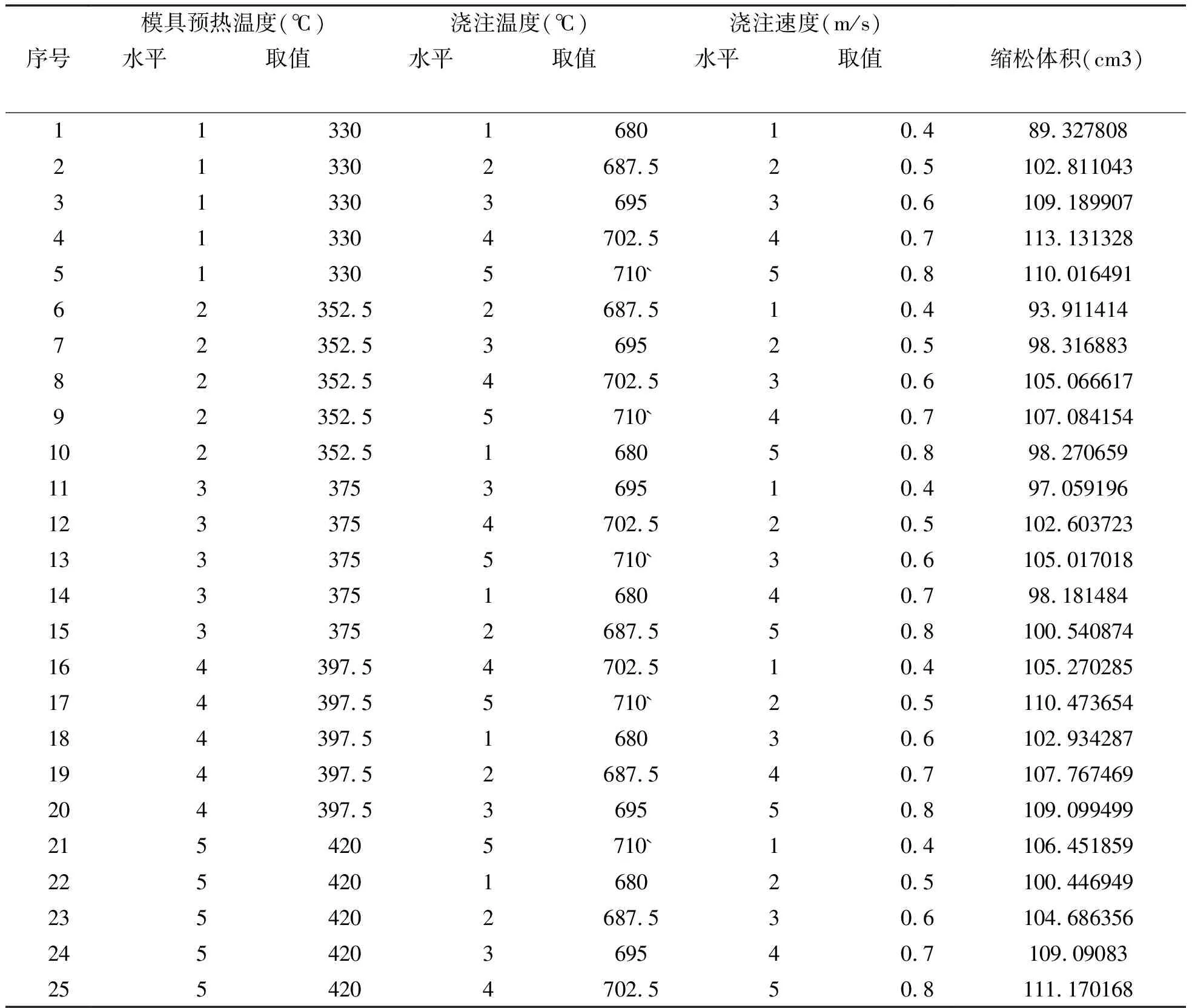
表3 正交试验条件下的轮毂铸造缩松情况
2 基于QPSO的支持向量机
2.1 QPSO算法原理
标准QPSO的速度和位置更新公式为:
Vi,j(t+1)=w(t)Vi,j(t)+c1r1[Pi,j(t)-Xi,j(t)] +c2r2[Pg,j(t)-Xi,j(t)]
(1)
Xi,j(t+1)=Xi,j(t)+Vi,j(t+1)
(2)
上式中,*i,j(t),*=V,P,X等表示第t次迭代粒子i第j维*分量,c1,c2为加速度常数,用于调整学习步长,r1,r2为[0,1]之间的随机数.Vi,j一般在限制在[Xmin,Xmax].

φi,j(t)~U(0,1),1≤j≤N,则粒子收敛时以点pi(t)=(pi,1(t),pi,2(t),…,pi,N(t).)为吸引且pi(t)为pbest和gbest间的随机值,其表达式为:
pi,j(t)=φi,j(t)Pi,j(t)+(1-φi,j(t))Pg,j(t)
(3)
在迭代过程中,粒子不断的靠近并最终到达点pi.因此,在迭代过程时,如果存在着一种势能(吸引势)在引导粒子向着pi点靠近,从而保证了整个粒子群体的聚集性,而不会趋向无穷大.
具有量子行为的粒子群算法的位置更新方程表达式为:
(4)
本文中采用Li,j(t)=2α|Cj(t)-Xi,j(t)|,α为扩张—收缩因子,QPSO方程可转换为:
Xi,j(t+1)=pi,j(t)±α|Cj(t)-Xi,j(t)|ln(1/ui,j(t)),ui,j(t)~U(0,1)
(5)
pi,j(t)=Pg,j(t)+φi,j(t)[Pi,j(t)-Pg,j(t)]
(6)
(7)
2.2 支持向量回归机(SVR)
对于样本集D={(xi,yi)|i=1,2,...l},其中xi∈Rn为n输入变量,yi∈R为输出变量.支持向量回归拟合采用回归函数f(x)=wx+b对样本点进行拟合,w为函数的广义参数,b为偏置值.引入ξi和ξi*两个非负松弛因子来允许拟合误差,则函数的拟合问题转化为优化问题:
(8)
(9)
基于最优化理论中的对偶原理,则可得到其对偶形式为:
(10)
(11)
根据式(9)和(10),则有支持向量回归机拟合表达式为:
(12)
在拟合非线性问题时需要采用非线性映射,将拟拟合的数数据通过非线性映射到高维特征空间后进行线性回归,同时在高维特征空间中进行线性回归时用核函数替代线性问题中的内积运算,即:
K(xi,xj)=φ(xi)φ(xj)
(13)
最后得到支持向量回归机拟合表达式为:
(14)
本文支持向量回归机的核函数选用高斯径向基核函数:
(15)
本文采用QPSO算法对SVR模型的参数进行优化, 以提高其拟合精度,基于QPSO算法的SVR预测模型改进流程如图6所示.
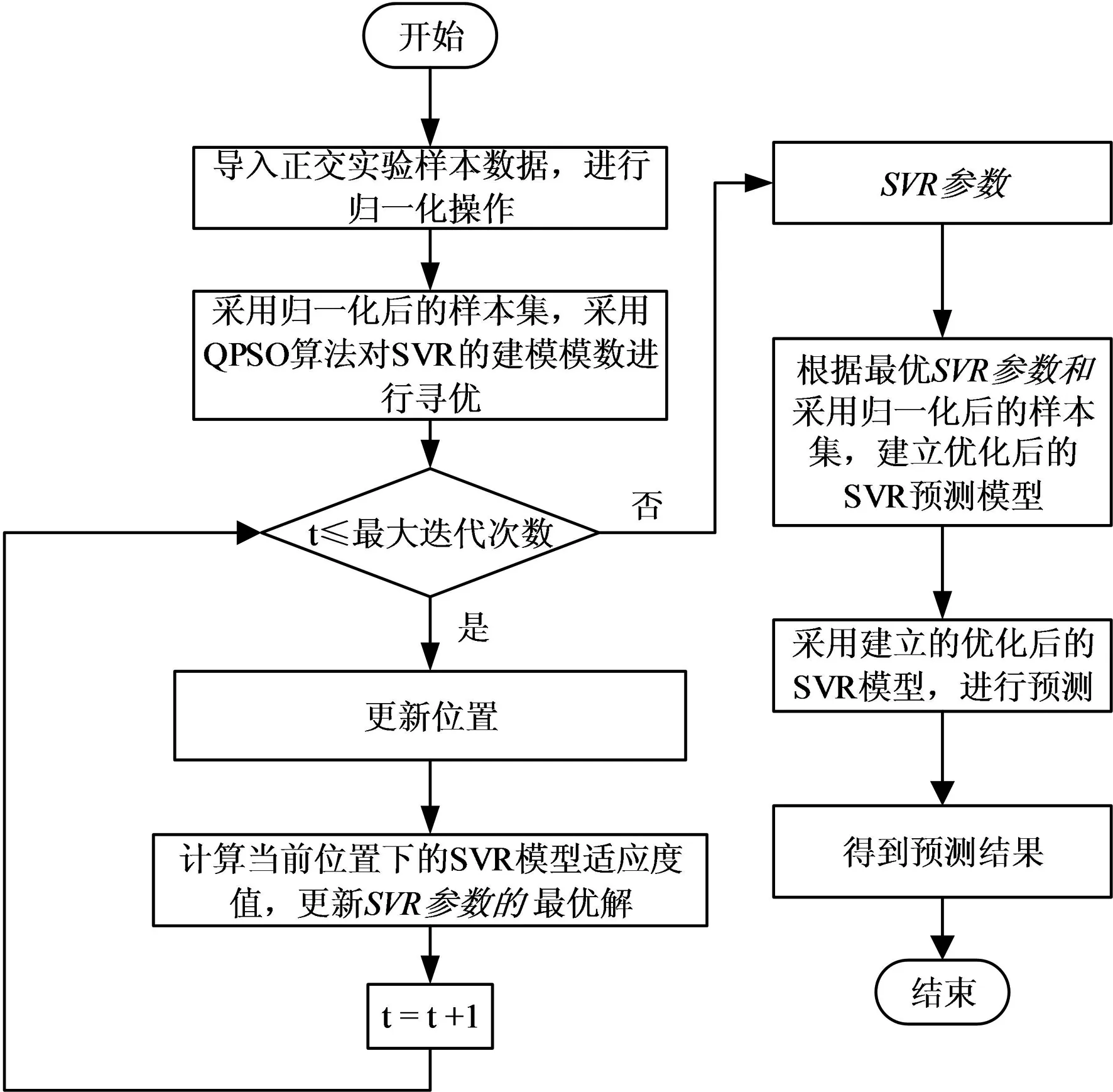
图5 基于QPSO算法的SVR建模流程
3 数值仿真
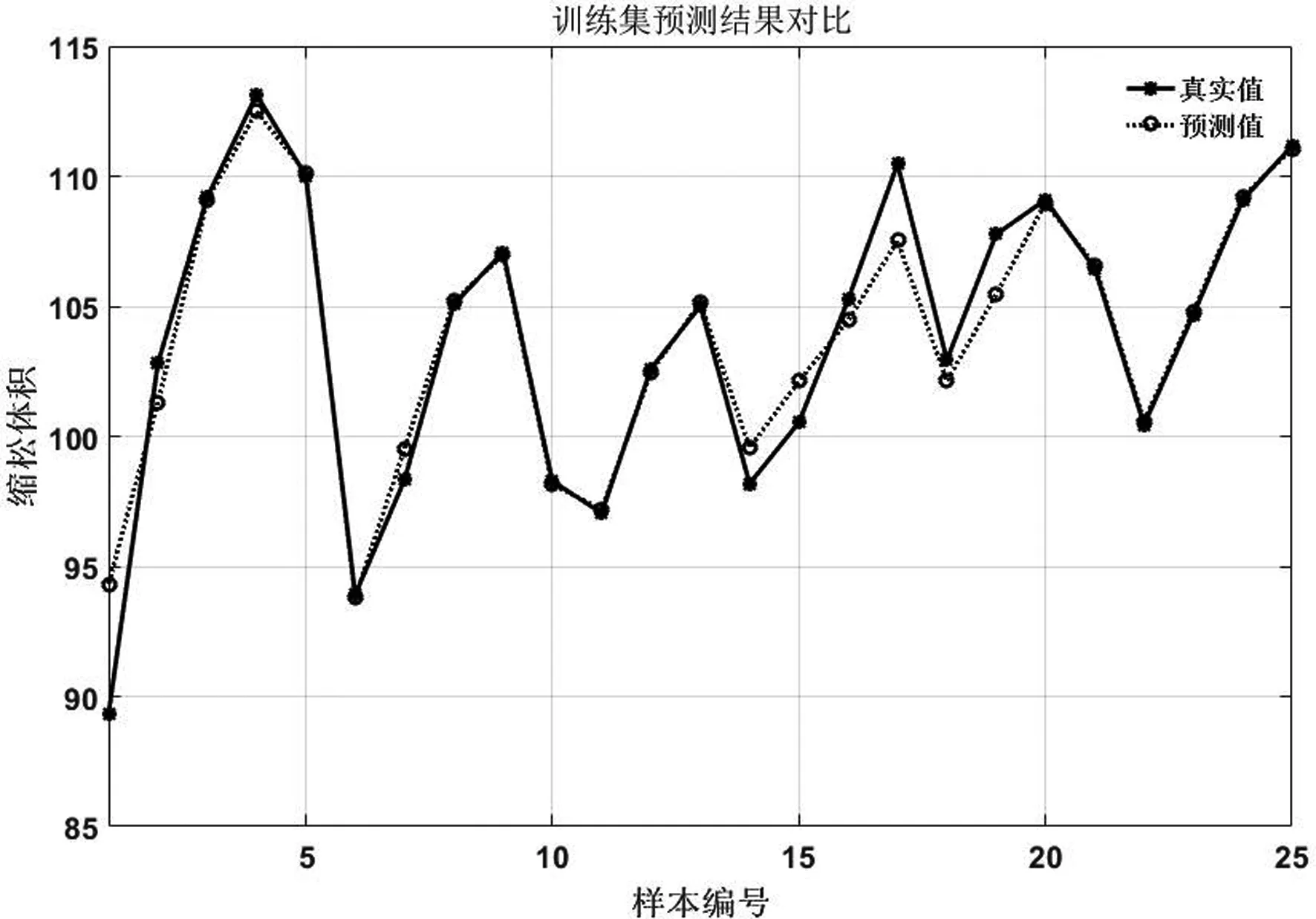
为验证本文所提出算法,采用MATLAB,分别实现基于SVR模型和基于QPSO算法改进的SVR模型建立轮毂铸造缩松缺陷的预测模型,基于SVR模型和基于QPSO算法改进的SVR模型的轮毂铸造缩松缺陷预测效果如图7所示.图7 优化前后轮毂铸造缩松缺陷预测效果(训练集),其中(a)为基于SVR模型的轮毂铸造缩松缺陷预测效果,图(b)为基于QPSO算法改进的SVR模型轮毂铸造缩松缺陷预测效果.从图7中,可以看到采用QPSO改进后的SVR的模型的拟合精度更高.
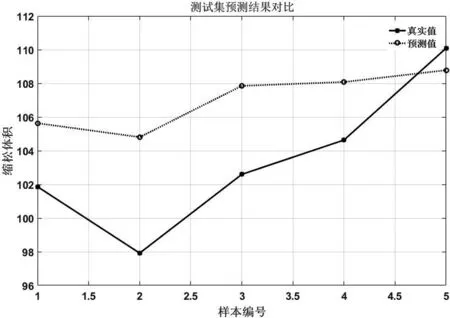
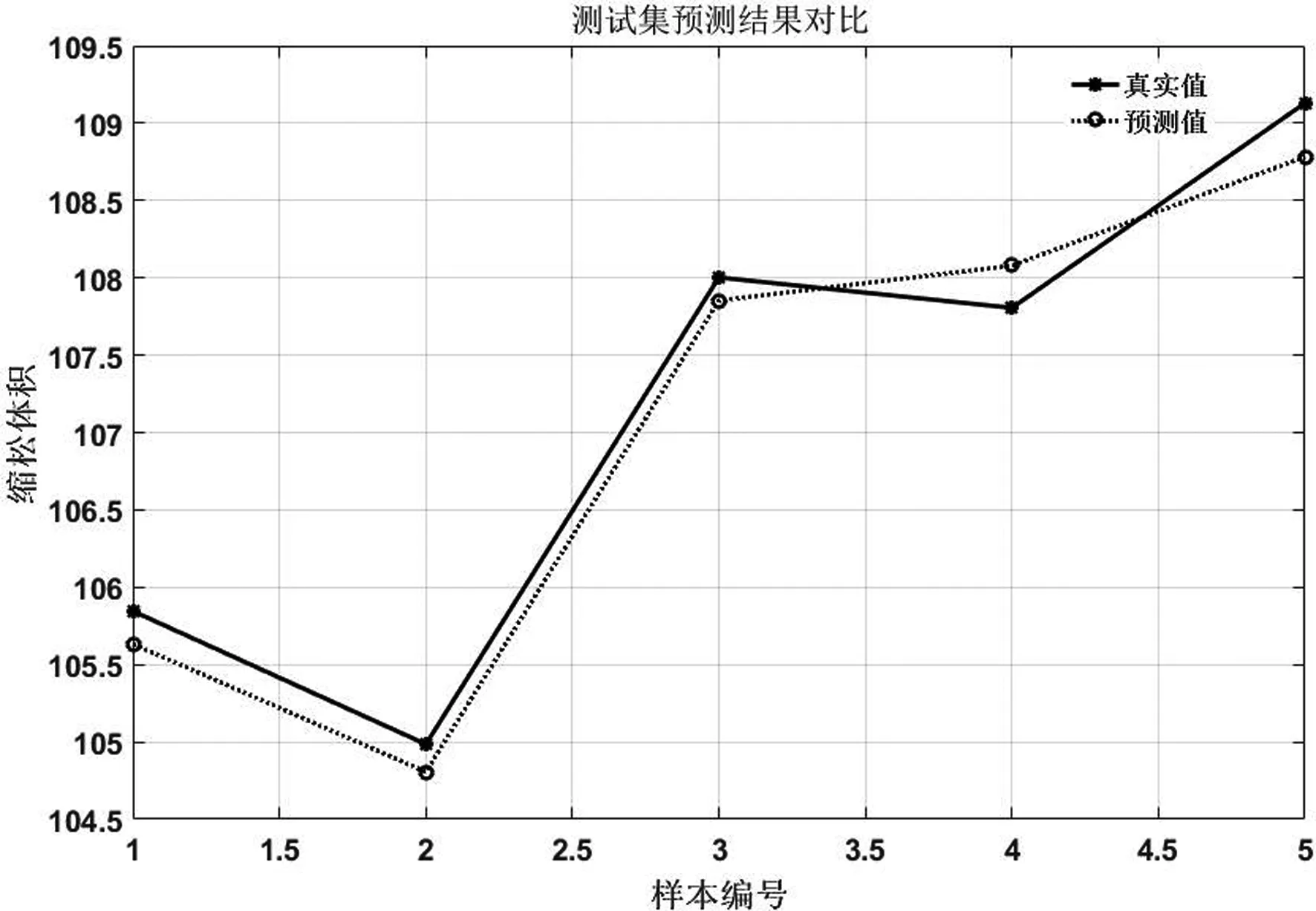
同时随机选取5组模具预热温度、浇注温度、浇注速度三个工艺参数的组合,采用PROCAST分析其轮毂铸造缩松缺陷情况,采用基于SVR模型和基于QPSO算法改进的SVR模型建立轮毂铸造缩松缺陷的预测模型进行预测,基于SVR模型和基于QPSO算法改进的SVR模型的轮毂铸造缩松缺陷预测效果如图8所示.图8优化前后轮毂铸造缩松缺陷预测效果(测试集),其中(a)为基于SVR模型的轮毂铸造缩松缺陷预测效果,图(b)为基于QPSO算法改进的SVR模型的轮毂铸造缩松缺陷预测效果.图9优化前后轮毂铸造缩松缺陷预测效果(测试集)箱型图,其中(a)为基于SVR模型的轮毂铸造缩松缺陷预测箱型图,图(b)为基于QPSO算法改进的SVR模型的轮毂铸造缩松缺陷预测箱型图.
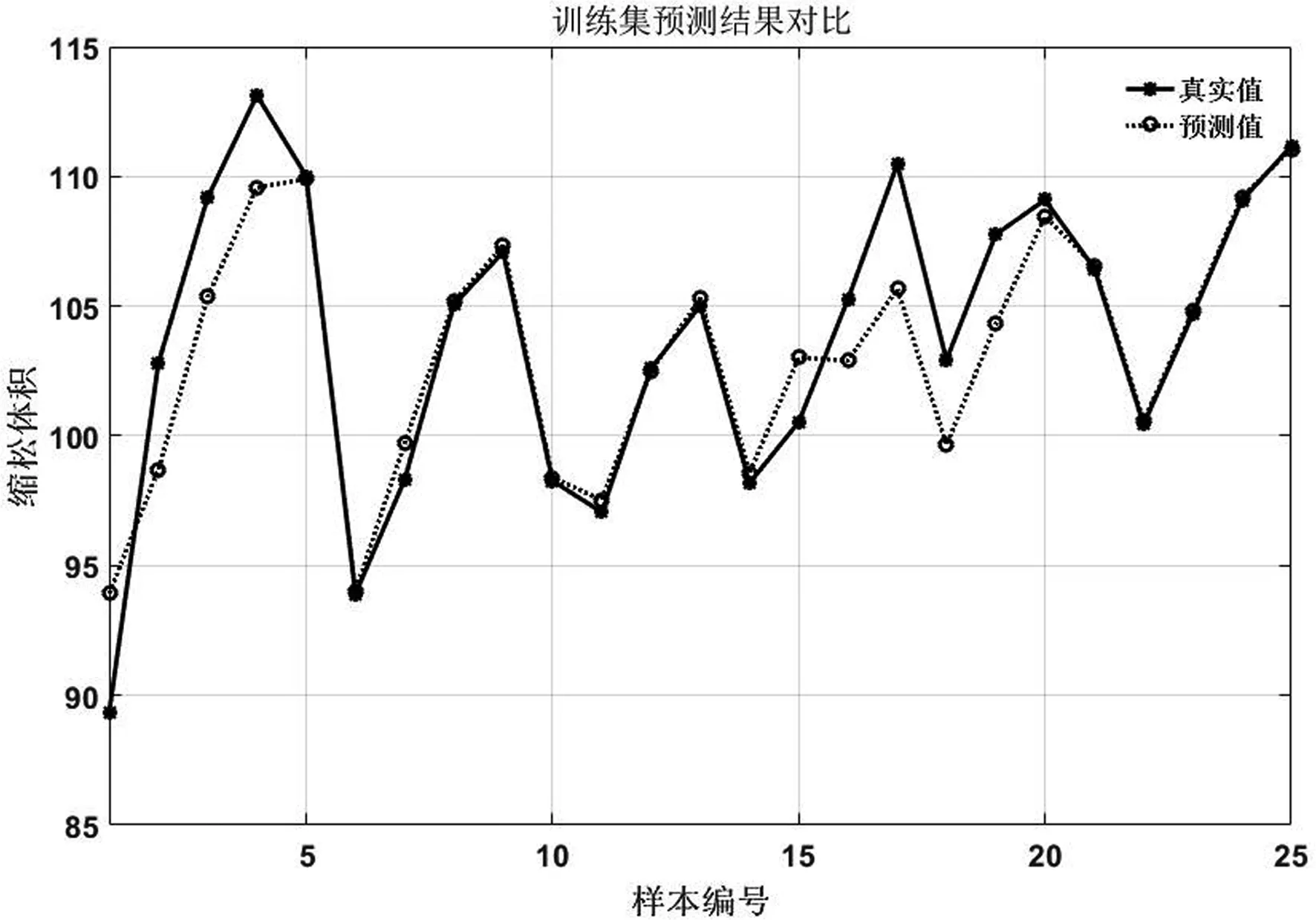
(a)
(b)
(a)
(b)

从图8-图9可以看到,改进后的SVR模型能够更好的预测模具预热温度、浇注温度、浇注速度在不同水平下的缩松体积,同时其结果与PROCAST软件模拟分析结果对比如表4所示.
如表4 所示,基于SVR模型和基于QPSO算法改进的SVR模型建立的轮毂铸造缩松缺陷预测模型均能很好的实现轮毂铸造缩松缺陷预测效果,但是从预测的误差来看,基于QPSO算法改进的SVR模型建立的轮毂铸造缩松缺陷预测模型其预测相对误差更小,则说明本文建立的预测模型产生的预测结果与有限元分析结果基于一致..
结 论
本文提出了一种基于QPSO-SVR算法的轮毂低压铸造缩松缺陷体积预测数学模型,利用SVR算法建立低压铸造工艺(模具预热温度、浇注温度、浇注速度)与缩松缺陷体积之间的数学模型,同时利用QPSO对SVR 算法的参数进行优化,提高数学模型的精度,并利用有限元方法验证数学模型的正确性.
(1)与传统的SVR模型相比,基于QPSO算法的改进后的SVR模型拟合精度更高.
(2)基于QPSO-SVR算法建立的轮毂低压铸造缩松缺陷体积预测数学模型与有限元的分析结果之间的相对误差更小,则说明本文建立的预测模型产生的预测结果与有限元分析结果基于一致.
(3)基于QPSO-SVR算法建立的轮毂低压铸造缩松缺陷体积预测数学模型为工艺参数的优化提供了更加准确的数学模型.
