基于参数敏感性分析的斜拉桥转体施工线形控制

崔怡观 宋 雨 谢 欢

(厦门大学建筑与土木工程学院 福建厦门 361005)

0 引言

随着我国城市化的发展，越来越多的跨线桥采用转体施工法，最大程度上减小对既有线路正常交通运营的影响。20世纪50年代初，桥梁转体施工控制技术在国外开始应用到实际工程中，如美国的P-K大桥和加拿大的Annacis大桥。日本在20世纪80年代末开始研发桥梁转体施工控制自动监测系统，与计算机网络结合，开发出一套可以进行参数敏感性分析与调整的斜拉桥施工双控系统[1]。斜拉桥转体施工控制技术在我国发展相对较晚，现阶段对桥梁转体施工的控制理论主要集中于连续梁桥及拱桥，在《公路桥涵施工技术规范》中，也仅有阐述拱桥转体施工的条文规定[2]。而近年来跨线桥梁结构形式中出现较多的斜拉桥桥型，因此，有必要针对斜拉桥转体施工控制技术进行研究，探索有效的施工控制方法。

斜拉桥转体施工过程中存在各种问题，如主塔偏位、主梁高差、应力变化等，与设计目标值存在一定的偏差，使得结构的实际状态包括结构的内力和几何线形等难以达到理想设计状态[3]。如果不及时进行有效控制和调整，偏差会不断累积，导致最后的成桥状态达不到设计要求，影响大桥的使用，严重时将造成工程事故[4-5]。

本文利用龙岩大桥有限元模型，采用归一化数据分析方法，对敏感性参数的影响程度进行计算和排序，得出对主梁线形影响最大的参数。同时引入BP神经网络，利用其自适应学习能力、非线性映射能力强以及容错能力高的特点[6]，对斜拉索索力进行优化调整，使主梁线形更接近理想状态，确保顺利对接合龙，探究斜拉桥转体施工控制的有效方法。

1 工程概况及桥梁有限元模型

龙岩大道高架桥工程南起西陂路交叉口，终点至爱亭路交叉口，全长2.4 km。主桥为(190+150) m的独塔斜拉索转体桥，桥面宽36.2 m，总体布置如图1所示。

图1 主桥桥型布置图(单位：m)

主桥采用独塔双索面钢箱梁斜拉桥构造，主梁采用扁平闭口流线型钢箱结构，主塔采用“宝石”型钢筋混凝土结构。主跨主梁转体悬臂长为173.35 m，次跨主梁转体悬臂长149.7 m，总计323.45 m。为充分利用有限施工场地，主桥施工采用“二次转体”方案，如图2～图3所示，先按主塔横轴线与线路中心线重合进行主塔施工，待塔柱施工完成后进行第一次69°单塔转体，将主塔转体使其垂直既有铁路线。一次转体后沿铁路平行线进行钢箱梁顶推施工，待钢箱梁顶推完成后，进行第二次21°主桥转体，将主桥转体至设计位置。

图2 主塔转体前平面示意 图3 主塔一次转体后平面示意图

根据设计图纸，主梁和索塔采用梁单元进行模拟。根据实际施工节段、截面材料尺寸等将全桥划分为466个结点，364个单元，建立成桥阶段有限元模型，如图4所示。其中斜拉索模拟采用只受拉桁架单元。

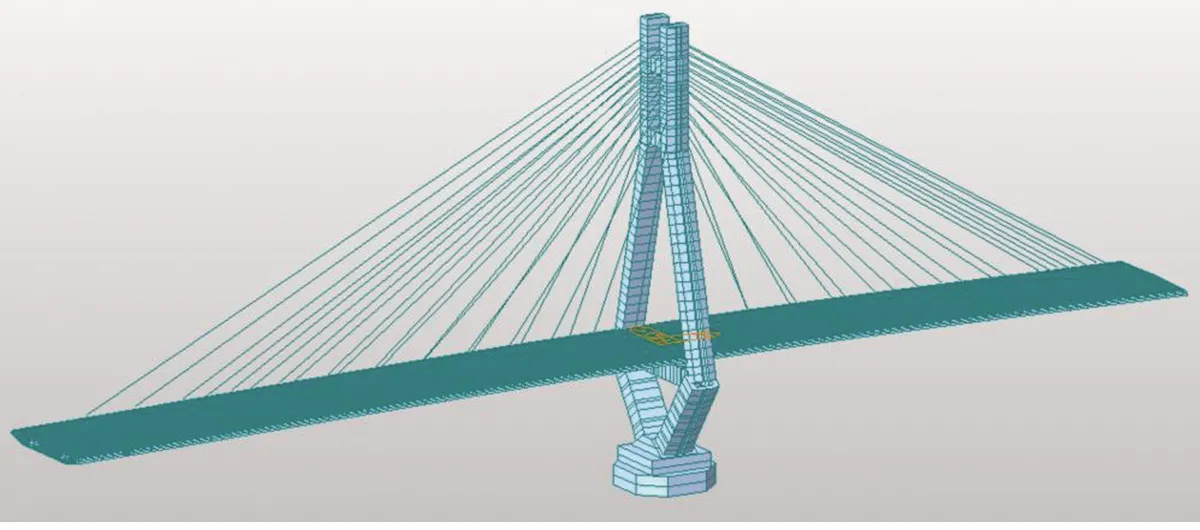
图4 龙岩大桥有限元模型

2 基于参数敏感性分析的转体施工线形控制方法

2.1 施工敏感性参数及归一化分析

斜拉桥主梁线形控制是主桥施工过程中的关键环节，如果主梁线形偏差过大，会导致合龙困难。已有研究结果及工程经验表明，斜拉桥转体施工过程中主梁自重误差、斜拉索初拉力、温差变化、桥塔偏位等敏感性因素会对主梁线形产生重要影响[7-8]。因此，在设计基准值的基础上，对上述敏感性因素进行改变，由桥梁有限元模型计算可得到相应主梁线性控制目标变化量[9-10]。各影响因素及对应的控制改量如表1所示。

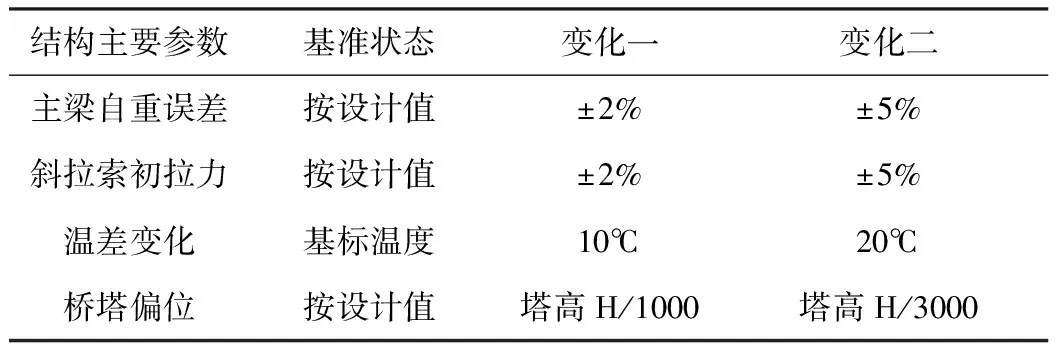
表1 转体施工影响因素与控制目标表

为进一步精准定义各敏感性因素的重要程度，应对其进行影响程度分析及排序，采用归一化处理方法，通过计算不同变化量下各敏感性因素的变化值总和，再对比各敏感性因素变化值总和的影响大小来对各因素排序[11]。定义：

β=∑|Xi-X0|

其中，Xi表示变化后主梁节段位移值大小，X0表示基准状态下主梁节段位移值大小。β表示所有线形变化值绝对值总和。归一化公式如下：

其中ω反应待研究的目标敏感性因素对某一控制要素的影响程度，βmax表示模拟样本库中的最大值，βmin表示模拟样本库中的最小值。

2.2 基于BP神经网络的参数识别及修正

BP神经网络按误差反向传播，可设置对应目标值输出偏差或训练次数。当两者之一达到既定目标时，判定神经网络学习结束，从而得到需要的结果。为保证桥梁转体后主梁线形达到理想状态，可利用BP神经网络对主梁线形实测值与目标值偏差进行参数识别，得出调整索力的大小，有效且快速满足主梁线形合龙要求[12]。

BP神经网络在工程中广泛应用，具有非线性映射能力强、适用性广、计算量小等特点，但也会呈现出收敛速度低、易陷入局部最小状态、样本数量质量要求高等缺陷。为使BP神经网络具有更高的易用性，对其进行优化[13]。

式中，ΔW表示权值修正值大小，n表示迭代次数，mc表示动量因子，一般取接近1的常数，λ为学习速率。在实际计算过程中，学习速率选取不当，会导致网络无法理想收敛；而动量因子mc也会对网络收敛速度产生影响，如果过大则可能使得网络发散，如果过小则导致收敛速度太慢。根据经验，一般取λ=0.2～0.5，mc=0.90～0.98，在该范围内算法收敛速度比较理想。

运用Matlab软件中内置的神经网络工具箱函数，对斜拉桥转体施工主梁线形控制BP神经网络分析进行编程并进行优化。在转体平衡称重后，选择主梁端部高程作为研究对象，选取合龙段附近悬臂端位移值作为输入神经元。根据各施工敏感性因素归一化分析结果，考虑到简化运行速度和计算量，以消除次要因素对神经网络带来的不利影响，所以在诸多影响斜拉桥转体施工线形控制的敏感性因素中，挑选出影响程度最高的敏感性因素，作为输出神经元[14]。

通过对建立的神经网络进行样本训练和检验，模拟参数识别的过程,复核模拟的可靠性。通过建立检验神经元样本A和输出神经元向量Y，进行神经网络检验。

Y=sim(net,A)

将Y中参数进行反归一化，得到神经网络识别的计算结果，通过对比检验样本中的计算值和理论值，利用吻合度来反映参数识别的精确度。

3 转体施工线形控制分析

3.1 斜拉索初拉力对主梁线形的影响

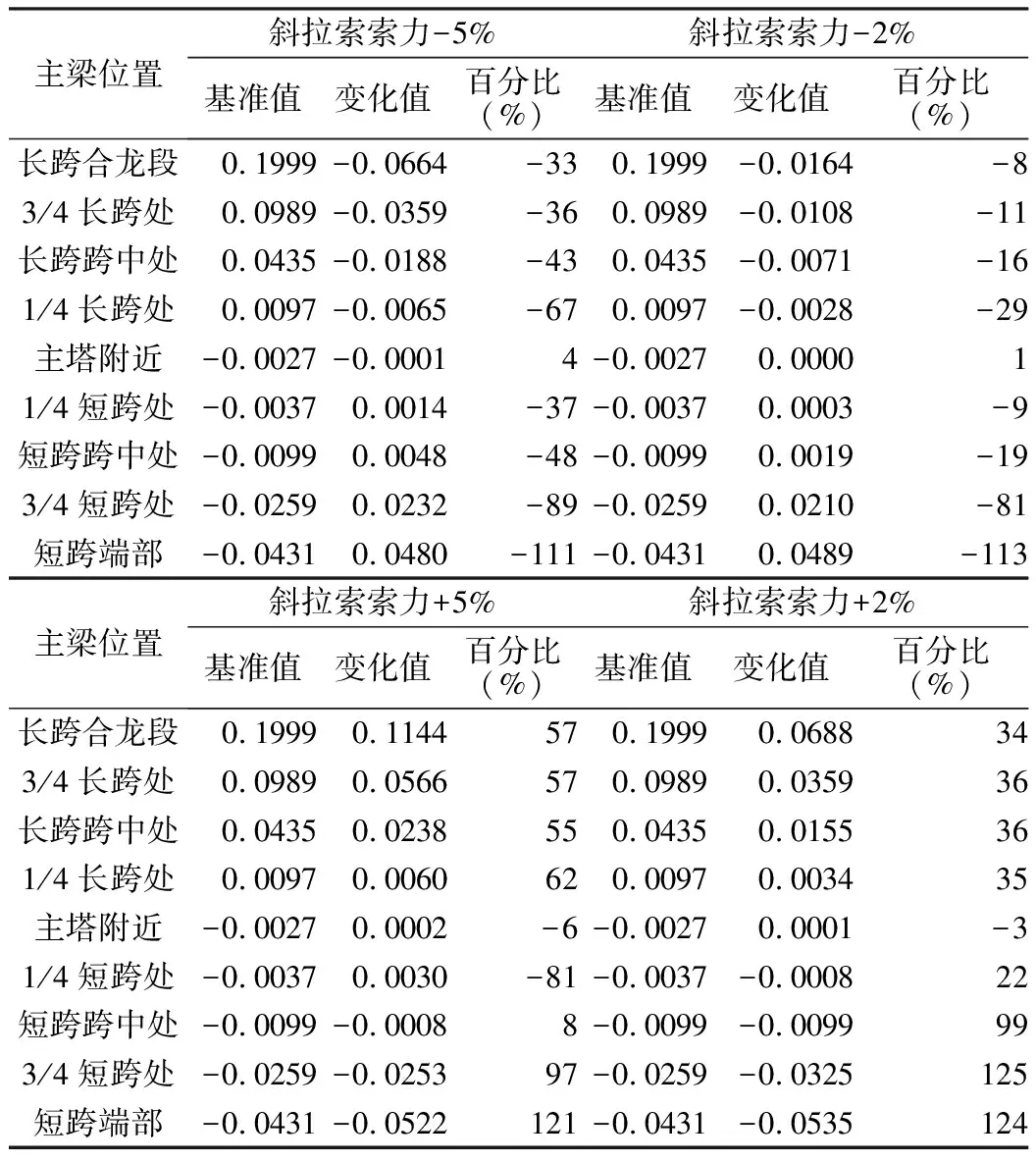
索力设计值如表2所示，M1～M11为长跨边斜拉索索力，S1～S11为短跨边斜拉索索力。在索力变化影响下，主梁线形变化情况如图5(a)所示。由图可见，随着索力变化值增大，主梁线形变化幅度也随之增加。由于主塔两侧跨径不同，斜拉索布置不对称，导致长短跨间线形变化程度不一致。取变化值量值与基准值百分比进行汇总对比，如表3所示。其中基准值为按上表1中基准状态的取值，变化值=改变参数后目标值-初始目标值。

表2 设计索力 k

m

当斜拉索索力增大5%时，二次转体后主梁线形变化值在-0.0522～+0.1144 m之间，线形变化值的最大绝对值出现在长跨合龙段。当斜拉索索力减小5%时，主梁线形变化值在-0.0644～+0.0480 m之间，线形变化值的最大绝对值出现在长跨合龙段。当斜拉索索力增大2%时，二次转体后主梁线形变化值在-0.0535～+0.0688 m之间，线形变化值的最大绝对值出现在长跨合龙段。当斜拉索索力减小2%时，主梁线形变化值在-0.0164～+0.0489 m之间，线形变化值的最大绝对值出现在短跨端部。

3.2 其他因素对主梁线形的影响

在温度变化、桥塔偏位和主梁自重因素变化影响下，主梁线形变化图如图5(b)、5(c)、5(d)所示，可看出桥塔偏位对主梁线形影响较大，最大变化值为80 mm，其余两个参数温度变化和主梁自重变化下，主梁线形最大变化值分别为7 mm和5 mm。

(a)斜拉索索力变化时主梁线形变化值

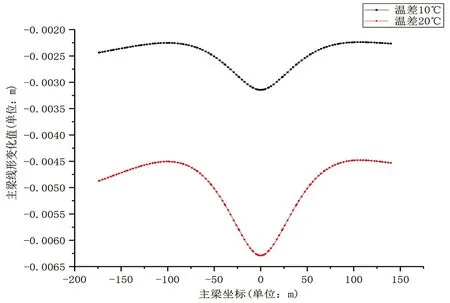
(b)温差变化时主梁线形变化值

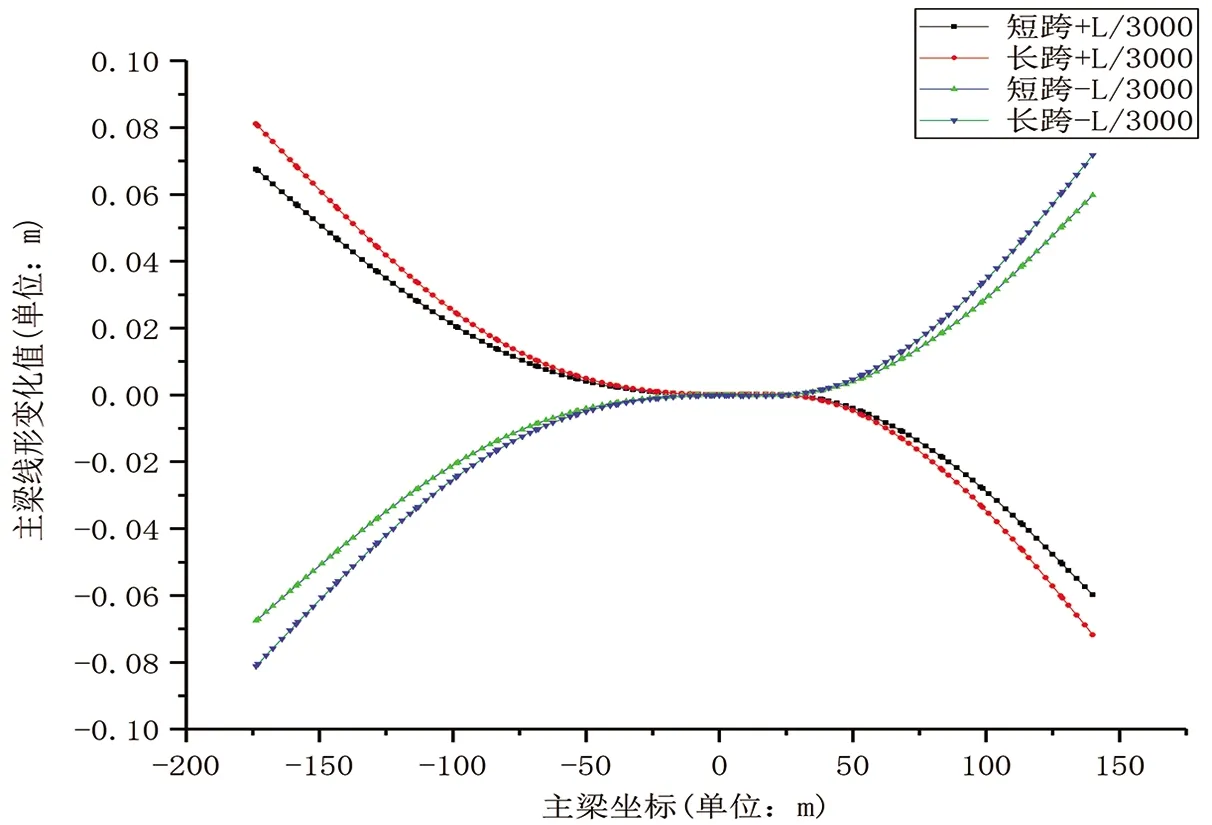
(c)主塔偏位时主梁线形变化值

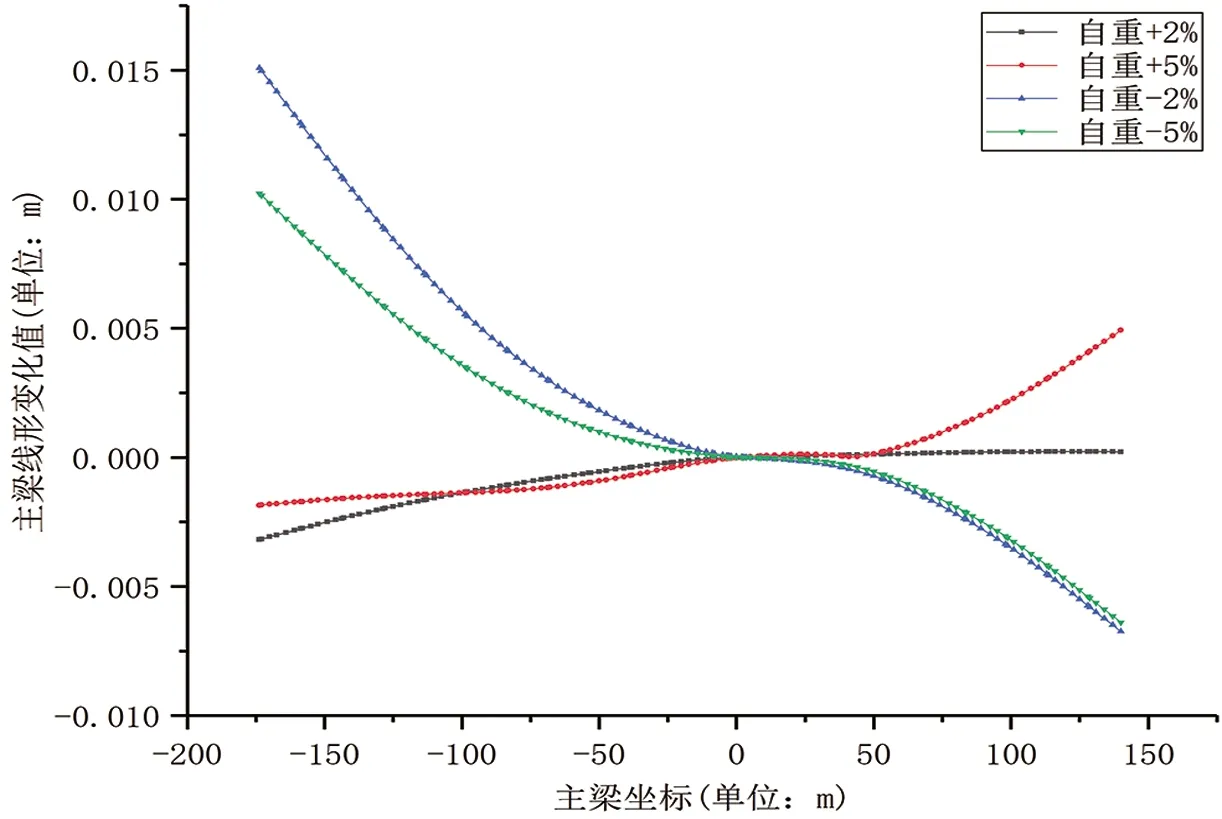
(d)主梁自重变化时主梁线形变化值

3.3 敏感性因素归一化分析及BP神经网络建立

各敏感性因素β值以及影响程度ω的大小如表4所示。

表4 敏感性因素归一化计算结果 mm

由表4可知，各施工敏感性参数中，斜拉索初拉力对主桥二次转体线形影响程度最大。为调整主梁线形，最有效的措施为对斜拉桥索力进行调整。大桥共有11对斜拉索，对每组拉索进行单独分析，以端部位移为控制点，计算主桥二次转体阶段线形差值。各对索敏感性因素β值及影响程度ω大小如表5所示。

由表5可见，索编号为M11、M10、M9、S8、S9、S10的斜拉索对主梁线形影响程度最为明显。因此选择这6组斜拉索作为主梁线形控制的关键因素。

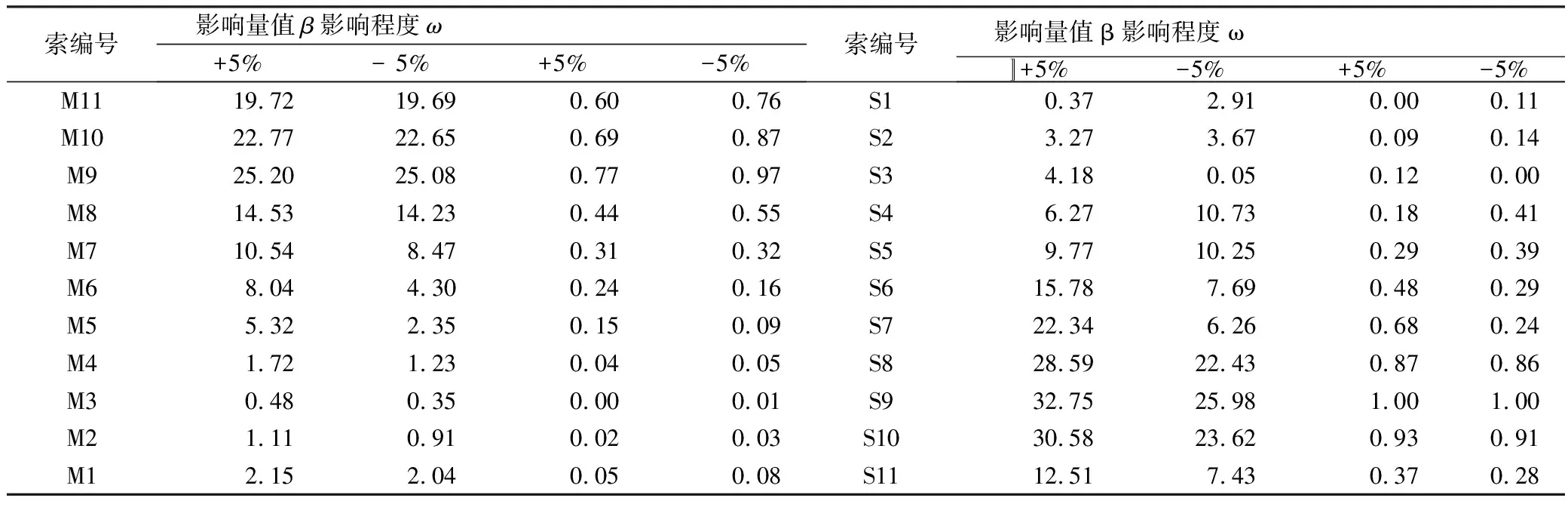
表5 单组索力归一化计算结果 mm

将该斜拉索初拉力作为输出神经元，输入神经元选择合龙段附近悬臂端位移值。运用Matlab软件，对斜拉桥转体施工主梁线形控制BP神经网络分析进行编程，其训练误差收敛趋势运行结果如图6所示，神经网络训练次数达到1447次后，收敛于10-9。

图6 训练误差收敛趋势

对建立好的神经网络进行检验，对比斜拉索索力的理论值和神经网络计算值，在24组中吻合度在90%以上的有13组，其余吻合度都在80%～90%之间，如表6所示。检验结果较理想，可以用于下一步对实际工程的参数识别和线形控制。吻合度=100%-(计算值-理论值)/理论值。

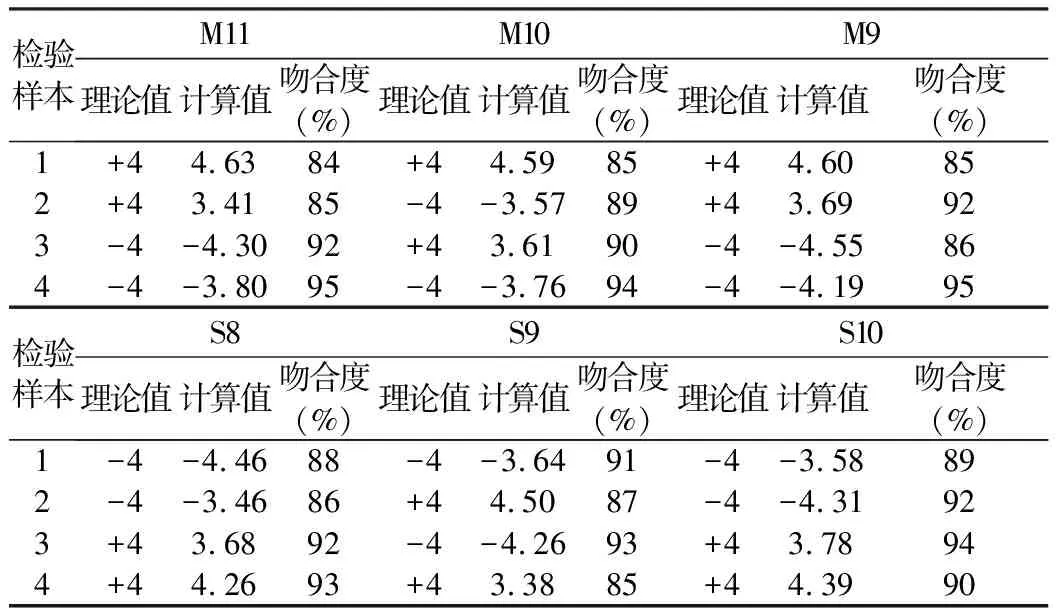
表6 神经网络检验结果归纳表

3.4 工程参数识别和大桥线形控制

将检验完成的BP神经网络应用于龙岩大桥二次转体主梁线形控制中,根据设计理想线型要求，输入合龙段附近高程，作为参数识别样本，如表7所示。

表7 二次转体阶段合龙段设计挠度

运行已有的BP神经网络程序，按照参数识别的结果，调整转体施工阶段的索力张拉值，得出用于主桥二次转体施工阶段的索力调整值，与设计索力值对比，如表8所示。

表8 参数识别修正后的索力调整值

把经BP神经网络识别后，得到的二次转体斜拉索索力调整值，代入Midas Civil中模拟验算，得出转体施工阶段主桥模拟结果，将计算模拟得到的主梁位移值与设计目标值进行对比，如图7和表9所示。

图7 索力识别调整后主梁线形模拟图

表9 索力识别调整后主梁变形数据表 m

由表9中位移值与目标值对比可看出，整体吻合度较高，主梁线形得到大幅优化，能够确保在转体施工过程中顺利对接合龙。同时说明BP神经网络分析方法在龙岩大桥转体施工线形控制中，取得较为理想的结果。

4 结语

本文建立龙岩大桥有限元分析模型，对主桥第二次转体阶段各施工影响因素进行敏感性分析，利用BP神经网络进行参数识别并优化调整，得到斜拉索索力调整方案，以实现主梁线形的有效控制，并得出以下结论：

(1)桥塔偏位和斜拉索初拉力对主梁线形变化的影响程度较高。对各敏感性参数进行归一化分析，进一步看出斜拉索初拉力对转体阶段主梁线形具有最大影响，并比较得到对主梁线形影响最大的6组斜拉索索力。

(2)利用BP神经网络对斜拉索索力进行优化调整，并应用到龙岩大桥的参数识别和主梁线形控制当中。根据输出结果与设计目标值对比的情况，整体吻合度高，有效且快速得到斜拉索索力优化调整值以及主梁调整线形，有利于主梁顺利对接合龙。